Уравнение неразрывности - Continuity equation

А уравнение неразрывности в физике уравнение который описывает транспортировку некоторого количества. Это особенно просто и эффективно, когда применяется к сохраненное количество, но его можно обобщить и применить к любому большое количество. С масса, энергия, импульс, электрический заряд и другие естественные величины сохраняются при соответствующих соответствующих условиях, различные физические явления могут быть описаны с помощью уравнений неразрывности.

Уравнения неразрывности - более сильная локальная форма законы сохранения. Например, слабая версия закона сохранение энергии утверждает, что энергия не может быть ни создана, ни уничтожена, т. е. общее количество энергии во Вселенной фиксировано. Это утверждение не исключает возможности того, что некоторое количество энергии могло исчезнуть из одной точки, одновременно появившись в другой точке. Более сильное утверждение состоит в том, что энергия локально сохранен: энергия не может быть ни создана, ни уничтожена, ни может это "телепорт "из одного места в другое - он может перемещаться только непрерывным потоком. Уравнение неразрывности - это математический способ выразить этот вид утверждения. Например, уравнение неразрывности для электрический заряд утверждает, что количество электрического заряда в любом объеме пространства может измениться только на величину электрический ток втекающий в этот объем или из него через его границы.

В более общем смысле уравнения непрерывности могут включать в себя термины «источник» и «сток», которые позволяют им описывать величины, которые часто, но не всегда, сохраняются, например, плотность молекулярных частиц, которые могут быть созданы или разрушены химическими реакциями. В повседневном примере есть уравнение непрерывности для количества живых людей; у него есть «исходный термин» для объяснения рождения людей и «поглотительный термин» для объяснения смерти людей.

Любое уравнение неразрывности можно выразить в «интегральной форме» (через интеграл потока ), который применяется к любой конечной области, или в «дифференциальной форме» (в терминах расхождение оператор), который применяется в точке.

Уравнения неразрывности лежат в основе более конкретных уравнения переноса такой как уравнение конвекции-диффузии, Уравнение переноса Больцмана, и Уравнения Навье – Стокса.

Потоки, описываемые уравнениями неразрывности, можно визуализировать с помощью Диаграмма Санки.

Общее уравнение

Определение потока

Основная статья: Поток

Уравнение неразрывности полезно, когда поток можно определить. Чтобы определить поток, сначала должна быть величина q которые могут течь или двигаться, например масса, энергия, электрический заряд, импульс, количество молекул и т. д. Пусть ρ быть объемом плотность от этого количества, то есть количество q на единицу объема.

То, как это количество q течет описывается его поток. Поток q это векторное поле, который мы обозначим как j. Вот несколько примеров и свойств флюса:

• Размер потока составляет «количество q протекает в единицу времени через единицу площади ». Например, в уравнении неразрывности массы для текущей воды, если 1 грамм воды в секунду течет через трубу с площадью поперечного сечения 1 см², то средний массовый поток j внутри трубы (1 грамм / секунда) / см², а его направление - вдоль трубы в направлении течения воды. Вне трубы, где нет воды, поток равен нулю.
• Если есть поле скорости ты который описывает соответствующий поток - другими словами, если все количество q в какой-то момент Икс движется со скоростью ты(Икс)- тогда поток по определению равен плотности, умноженной на поле скорости:

${\displaystyle \mathbf {j} =\rho \mathbf {u} }$

Например, если в уравнении неразрывности массы для текущей воды ты - скорость воды в каждой точке, а ρ - плотность воды в каждой точке, тогда j будет массовый поток.

• В хорошо известном примере поток электрический заряд это плотность электрического тока.

Иллюстрация того, как флюс j количества q проходит через открытую поверхность S. (dS дифференциальный векторная площадь ).

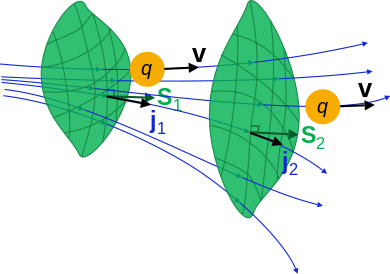
• Если есть воображаемая поверхность S, то поверхностный интеграл потока над S равно количеству q что проходит через поверхность S в единицу времени:

${\displaystyle ({\text{Rate that }}q{\text{ is flowing through the imaginary surface }}S)=\iint _{S}\mathbf {j} \cdot d\mathbf {S} }$

в котором ∬_S dS это поверхностный интеграл.

(Обратите внимание, что понятие, которое здесь называется «поток», в некоторой литературе также называется «плотностью потока», в этом контексте «поток» обозначает поверхностный интеграл плотности потока. См. Основную статью о Поток для подробностей.)

Интегральная форма

Интегральная форма уравнения неразрывности утверждает, что:

• Количество q в регионе увеличивается при дополнительном q течет внутрь через поверхность области и уменьшается, когда течет наружу;
• Количество q в регионе увеличивается при появлении новых q создается внутри региона и уменьшается, когда q уничтожен;
• Помимо этих двух процессов, существует другого варианта нет на сумму q в регионе, который нужно изменить.

Математически интегральная форма уравнения неразрывности, выражающая скорость роста q в объеме V является:

${\displaystyle {\frac {dq}{dt}}+}$ ${\displaystyle \scriptstyle S}$ ${\displaystyle \mathbf {j} \cdot d\mathbf {S} =\Sigma }$

куда

В интегральной форме уравнения неразрывности S есть ли закрытая поверхность который полностью охватывает объем V, как и любая из поверхностей слева. S может нет быть поверхностью с границами, как те, что справа. (Поверхности синие, границы красные.)

• S любой воображаемый закрытая поверхность, который включает объем V,
• S dS обозначает поверхностный интеграл над этой закрытой поверхностью,
• q это общая сумма количества в томе V,
• j это поток q,
• т время,
• Σ чистая ставка, которая q генерируется внутри объема V. Когда q создается, он называется источник из q, и это делает Σ более позитивный. Когда q разрушается, это называется раковина из q, и это делает Σ более отрицательный. Этот термин иногда записывают как ${\displaystyle dq/dt|_{\rm {gen}}}$ или полное изменение q от его образования или разрушения внутри контрольного объема.

В простом примере V может быть здание, и q может быть количество людей в здании. Поверхность S будет состоять из стен, дверей, крыши и фундамента здания. Тогда уравнение непрерывности утверждает, что количество людей в здании увеличивается, когда люди входят в здание (поток внутрь через поверхность), уменьшается, когда люди выходят из здания (поток наружу через поверхность), увеличивается, когда кто-то в здании дает рождение (источник, Σ > 0) и уменьшается, когда кто-то в здании умирает (раковина, Σ < 0).

Дифференциальная форма

Смотрите также: Закон сохранения и форма сохранения

Посредством теорема расходимости, общее уравнение неразрывности также можно записать в «дифференциальной форме»:

${\displaystyle {\frac {\partial \rho }{\partial t}}+\nabla \cdot \mathbf {j} =\sigma \,}$

куда

• ∇⋅ является расхождение,
• ρ это количество количества q на единицу объема,
• j это поток q,
• т время,
• σ это поколение q на единицу объема в единицу времени. Термины, которые создают q (т.е. σ > 0) или удалить q (т.е. σ < 0) называются «источниками» и «стоками» соответственно.

Это общее уравнение можно использовать для вывода любого уравнения неразрывности, от простого уравнения неразрывности объема до такого сложного, как уравнение неразрывности. Уравнения Навье – Стокса. Это уравнение также обобщает уравнение переноса. Другие уравнения в физике, например Закон Гаусса электрического поля и Закон Гаусса для гравитации, имеют математическую форму, аналогичную уравнению неразрывности, но обычно не упоминаются термином "уравнение неразрывности", поскольку j в этих случаях не представляет собой поток реальной физической величины.

В случае, если q это сохраненное количество которые не могут быть созданы или уничтожены (например, энергия ), σ = 0 и уравнения становятся:

${\displaystyle {\frac {\partial \rho }{\partial t}}+\nabla \cdot \mathbf {j} =0\,}$

Электромагнетизм

Основная статья: Сохранение заряда

В электромагнитная теория, уравнение неразрывности представляет собой эмпирический закон, выражающий (локальный) сохранение заряда. Математически это автоматическое следствие Уравнения Максвелла, хотя сохранение заряда более фундаментально, чем уравнения Максвелла. В нем говорится, что расхождение из плотность тока J (в амперы на квадратный метр) равна отрицательной скорости изменения плотность заряда ρ (в кулоны за кубический метр),

${\displaystyle \nabla \cdot \mathbf {J} =-{\partial \rho \over \partial t}}$

Согласованность с уравнениями Максвелла

Один из Уравнения Максвелла, Закон Ампера (с поправкой Максвелла), утверждает, что ${\displaystyle \nabla \times \mathbf {H} =\mathbf {J} +{\frac {\partial \mathbf {D} }{\partial t}}.}$ Взяв расхождение обеих сторон (расхождение и частную производную по времени коммутации), получаем ${\displaystyle \nabla \cdot (\nabla \times \mathbf {H} )=\nabla \cdot \mathbf {J} +{\frac {\partial (\nabla \cdot \mathbf {D} )}{\partial t}},}$ но расходимость завитка равна нулю, так что ${\displaystyle \nabla \cdot \mathbf {J} +{\frac {\partial (\nabla \cdot \mathbf {D} )}{\partial t}}=0.}$ Но Закон Гаусса (другое уравнение Максвелла) утверждает, что ${\displaystyle \nabla \cdot \mathbf {D} =\rho ,\,}$ которое можно подставить в предыдущее уравнение, чтобы получить уравнение неразрывности ${\displaystyle \nabla \cdot \mathbf {J} +{\partial \rho \over \partial t}=0.\,}$

Ток - это движение заряда. Уравнение неразрывности говорит, что если заряд движется из дифференциального объема (т. Е. Дивергенция плотности тока положительна), то количество заряда в этом объеме будет уменьшаться, поэтому скорость изменения плотности заряда будет отрицательной. Следовательно, уравнение неразрывности сводится к сохранению заряда.

Если магнитные монополи существует уравнение неразрывности для монопольных токов, см. статью о монополях, чтобы узнать об истории вопроса и двойственности между электрическим и магнитным токами.

Динамика жидкостей

Смотрите также: Поток массы, Массовый расход, и Уравнение завихренности

В динамика жидкостей, уравнение неразрывности утверждает, что скорость, с которой масса входит в систему, равна скорости, с которой масса покидает систему, плюс накопление массы внутри системы.^[1][2]Дифференциальная форма уравнения неразрывности:^[1]

${\displaystyle {\frac {\partial \rho }{\partial t}}+\nabla \cdot (\rho \mathbf {u} )=0}$

куда

• ρ жидкий плотность,
• т время,
• ты это скорость потока векторное поле.

Производную по времени можно понимать как накопление (или потерю) массы в системе, в то время как расхождение член представляет собой разницу между входящим и выходящим потоком. В этом контексте это уравнение также является одним из Уравнения Эйлера (гидродинамика). В Уравнения Навье – Стокса образуют векторное уравнение неразрывности, описывающее сохранение линейный импульс.

Если жидкость несжимаема (объемная скорость деформации равна нулю), уравнение неразрывности массы упрощается до уравнения неразрывности объема:^[3]

${\displaystyle \nabla \cdot \mathbf {u} =0,}$

что означает, что расхождение поля скорости всюду равно нулю. Физически это эквивалентно тому, что скорость расширения локального объема равна нулю, следовательно, поток воды через сходящуюся трубу будет регулироваться исключительно за счет увеличения его скорости, поскольку вода в значительной степени несжимаема.

Энергия и тепло

Сохранение энергии говорит, что энергия не может быть создана или уничтожена. (Видеть ниже для нюансов, связанных с общей теорией относительности.) Следовательно, существует уравнение неразрывности для потока энергии:

${\displaystyle {\frac {\partial u}{\partial t}}+\nabla \cdot \mathbf {q} =0}$

куда

• ты, местный плотность энергии (энергия на единицу объема),
• q, поток энергии (передача энергии на единицу площади поперечного сечения в единицу времени) как вектор,

Важным практическим примером является поток тепла. Когда тепло течет внутри твердого тела, уравнение неразрывности можно объединить с Закон Фурье (тепловой поток пропорционален градиенту температуры), чтобы получить уравнение теплопроводности. Уравнение теплового потока также может иметь исходные члены: Хотя энергия не может быть создан или уничтожен, высокая температура могут быть созданы из других видов энергии, например, с помощью трение или же джоулевое нагревание.

Распределения вероятностей

Если есть величина, которая непрерывно движется в соответствии со случайным (случайным) процессом, например, местоположение единственной растворенной молекулы с Броуновское движение, то существует уравнение неразрывности его распределение вероятностей. Поток в этом случае - это вероятность на единицу площади в единицу времени, что частица проходит через поверхность. Согласно уравнению неразрывности, отрицательная дивергенция этого потока равна скорости изменения плотность вероятности. Уравнение неразрывности отражает тот факт, что молекула всегда где-то - интеграл ее распределения вероятностей всегда равен 1, - и что она движется непрерывным движением (нет телепортация ).

Квантовая механика

Квантовая механика - еще одна область, в которой существует уравнение неразрывности, связанное с сохранение вероятности. Для членов уравнения требуются следующие определения, и они немного менее очевидны, чем в других примерах выше, поэтому они кратко описаны здесь:

• В волновая функция Ψ для одного частица в позиционное пространство (скорее, чем импульсное пространство ), то есть функция положения р и время т, Ψ = Ψ(р, т).
• В функция плотности вероятности является

  ${\displaystyle \rho (\mathbf {r} ,t)=\Psi ^{*}(\mathbf {r} ,t)\Psi (\mathbf {r} ,t)=|\Psi (\mathbf {r} ,t)|^{2}.}$

• В вероятность найти частицу внутри V в т обозначается и определяется как

  ${\displaystyle P=P_{\mathbf {r} \in V}(t)=\int _{V}\Psi ^{*}\Psi dV=\int _{V}|\Psi |^{2}dV.}$

• В ток вероятности (он же поток вероятностей)

  ${\displaystyle \mathbf {j} (\mathbf {r} ,t)={\frac {\hbar }{2mi}}\left[\Psi ^{*}\left(\nabla \Psi \right)-\Psi \left(\nabla \Psi ^{*}\right)\right].}$

С этими определениями уравнение неразрывности гласит:

${\displaystyle \nabla \cdot \mathbf {j} +{\frac {\partial \rho }{\partial t}}=0~\rightleftharpoons ~\nabla \cdot \mathbf {j} +{\frac {\partial |\Psi |^{2}}{\partial t}}=0.}$

Любая форма может быть указана. Интуитивно указанные выше величины указывают на то, что они представляют собой поток вероятности. В шанс найти частицу в некоторой позиции р и время т течет как жидкость; отсюда и термин ток вероятности, а векторное поле. Сама частица делает нет поток детерминированно в этом векторное поле.

Согласованность с уравнением Шредингера

3-х мерная зависимость Уравнение Шредингера и это комплексно сопряженный (я → −я повсюду) соответственно:[4] ${\displaystyle {\begin{aligned}-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\Psi +U\Psi &=i\hbar {\frac {\partial \Psi }{\partial t}},\\-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\Psi ^{*}+U\Psi ^{*}&=-i\hbar {\frac {\partial \Psi ^{*}}{\partial t}},\\\end{aligned}}}$ куда U это потенциальная функция. В частная производная из ρ относительно т является: ${\displaystyle {\frac {\partial \rho }{\partial t}}={\frac {\partial |\Psi |^{2}}{\partial t}}={\frac {\partial }{\partial t}}\left(\Psi ^{*}\Psi \right)=\Psi ^{*}{\frac {\partial \Psi }{\partial t}}+\Psi {\frac {\partial \Psi ^{*}}{\partial t}}.}$ Умножая уравнение Шредингера на Ψ* затем решение для Ψ* ∂Ψ/∂т, и аналогично умножая комплексно сопряженное уравнение Шредингера на Ψ затем решение для Ψ ∂Ψ*/∂т; ${\displaystyle {\begin{aligned}\Psi ^{*}{\frac {\partial \Psi }{\partial t}}&={\frac {1}{i\hbar }}\left[-{\frac {\hbar ^{2}\Psi ^{*}}{2m}}\nabla ^{2}\Psi +U\Psi ^{*}\Psi \right],\\\Psi {\frac {\partial \Psi ^{*}}{\partial t}}&=-{\frac {1}{i\hbar }}\left[-{\frac {\hbar ^{2}\Psi }{2m}}\nabla ^{2}\Psi ^{*}+U\Psi \Psi ^{*}\right],\\\end{aligned}}}$ подставив в производную по времени ρ: ${\displaystyle {\begin{aligned}{\frac {\partial \rho }{\partial t}}&={\frac {1}{i\hbar }}\left[-{\frac {\hbar ^{2}\Psi ^{*}}{2m}}\nabla ^{2}\Psi +U\Psi ^{*}\Psi \right]-{\frac {1}{i\hbar }}\left[-{\frac {\hbar ^{2}\Psi }{2m}}\nabla ^{2}\Psi ^{*}+U\Psi \Psi ^{*}\right]\\&={\frac {1}{i\hbar }}\left[-{\frac {\hbar ^{2}\Psi ^{*}}{2m}}\nabla ^{2}\Psi +U\Psi ^{*}\Psi \right]+{\frac {1}{i\hbar }}\left[+{\frac {\hbar ^{2}\Psi }{2m}}\nabla ^{2}\Psi ^{*}-U\Psi ^{*}\Psi \right]\\[2pt]&=-{\frac {1}{i\hbar }}{\frac {\hbar ^{2}\Psi ^{*}}{2m}}\nabla ^{2}\Psi +{\frac {1}{i\hbar }}{\frac {\hbar ^{2}\Psi }{2m}}\nabla ^{2}\Psi ^{*}\\[2pt]&={\frac {\hbar }{2im}}\left[\Psi \nabla ^{2}\Psi ^{*}-\Psi ^{*}\nabla ^{2}\Psi \right]\\\end{aligned}}}$ В Лапласиан операторы (∇^2) в приведенном выше результате предполагают, что правая часть - это дивергенция j, а обратный порядок членов подразумевает, что это отрицательное значение j, всего: ${\displaystyle {\begin{aligned}\nabla \cdot \mathbf {j} &=\nabla \cdot \left[{\frac {\hbar }{2mi}}\left(\Psi ^{*}\left(\nabla \Psi \right)-\Psi \left(\nabla \Psi ^{*}\right)\right)\right]\\&={\frac {\hbar }{2mi}}\left[\Psi ^{*}\left(\nabla ^{2}\Psi \right)-\Psi \left(\nabla ^{2}\Psi ^{*}\right)\right]\\&=-{\frac {\hbar }{2mi}}\left[\Psi \left(\nabla ^{2}\Psi ^{*}\right)-\Psi ^{*}\left(\nabla ^{2}\Psi \right)\right]\\\end{aligned}}}$ так что уравнение неразрывности: ${\displaystyle {\begin{aligned}&{\frac {\partial \rho }{\partial t}}=-\nabla \cdot \mathbf {j} \\\Rightarrow {}&{\frac {\partial \rho }{\partial t}}+\nabla \cdot \mathbf {j} =0\\\end{aligned}}}$ Интегральная форма аналогична общему уравнению.

Релятивистская версия

Специальная теория относительности

Смотрите также: 4-вектор

Обозначения и инструменты специальная теория относительности, особенно 4-векторы и 4-градиент, предлагают удобный способ написать любое уравнение неразрывности.

Плотность количества ρ и его нынешний j можно объединить в 4-вектор называется 4-текущий:

${\displaystyle J=\left(c\rho ,j_{x},j_{y},j_{z}\right)}$

куда c это скорость света. 4-расхождение этого тока:

${\displaystyle \partial _{\mu }J^{\mu }=c{\frac {\partial \rho }{\partial ct}}+\nabla \cdot \mathbf {j} }$

куда ∂_μ это 4-градиентный и μ является индекс маркировка пространство-время измерение. Тогда уравнение неразрывности:

${\displaystyle \partial _{\mu }J^{\mu }=0}$

в обычном случае, когда нет источников или стоков, то есть для совершенно сохраняемых величин, таких как энергия или заряд. Это уравнение неразрывности явно («очевидно») Инвариант Лоренца.

Примеры уравнений неразрывности, часто записываемых в такой форме, включают сохранение электрического заряда.

${\displaystyle \partial _{\mu }J^{\mu }=0}$

куда J электрический 4-текущий; и сохранение энергии-импульса

${\displaystyle \partial _{\nu }T^{\mu \nu }=0}$

куда Т это тензор энергии-импульса.

Общая теория относительности

В общая теория относительности, где пространство-время искривлено, уравнение неразрывности (в дифференциальной форме) для энергии, заряда или других сохраняющихся величин включает ковариантный расхождение вместо обычного расхождения.

Например, тензор энергии-импульса второго порядка тензорное поле содержащий плотности энергии-импульса, потоки энергии-импульса и касательные напряжения массово-энергетического распределения. Дифференциальная форма сохранения энергии-импульса в общей теории относительности утверждает, что ковариантный дивергенция тензора энергии-импульса равна нулю:

${\displaystyle {T^{\mu }}_{\nu ;\mu }=0.}$

Это важное ограничение на форму Уравнения поля Эйнштейна принимать общая теория относительности.^[5]

Тем не менее обычный расхождение тензора энергии-импульса нет обязательно исчезнут:^[6]

${\displaystyle \partial _{\mu }T^{\mu \nu }=-\Gamma _{\mu \lambda }^{\mu }T^{\lambda \nu }-\Gamma _{\mu \lambda }^{\nu }T^{\mu \lambda },}$

Правая часть строго исчезает только для плоской геометрии.

Как следствие, интеграл форму уравнения неразрывности трудно определить и не обязательно справедливо для области, в которой пространство-время значительно искривлено (например, вокруг черной дыры или во всей вселенной).^[7]

Физика элементарных частиц

Кварки и глюоны имеют цветной заряд, который всегда сохраняется как электрический заряд, и существует уравнение неразрывности для таких токов цветного заряда (явные выражения для токов приведены в тензор напряженности глюонного поля ).

В физике элементарных частиц есть много других величин, которые часто или всегда сохраняются: барионное число (пропорционально количеству кварков минус количество антикварков), число электрона, число мю, число тау, изоспин, и другие.^[8] Каждый из них имеет соответствующее уравнение неразрывности, возможно, включая члены источника / стока.

Теорема Нётер

Для более подробных объяснений и выводов см. Теорема Нётер.

Одна из причин того, что уравнения сохранения часто встречаются в физике: Теорема Нётер. Это означает, что всякий раз, когда законы физики имеют непрерывная симметрия, существует уравнение неразрывности для некоторой сохраняющейся физической величины. Три самых известных примера:

• Законы физики инвариантны относительно перевод времени - например, законы физики сегодня такие же, как вчера. Эта симметрия приводит к уравнению неразрывности для сохранение энергии.
• Законы физики инвариантны по отношению к перемещению в пространстве - например, законы физики в Бразилии такие же, как законы физики в Аргентине. Эта симметрия приводит к уравнению неразрывности для сохранение импульса.
• Законы физики инвариантны относительно ориентации - например, плавая в космическом пространстве, вы не можете измерить, "какой путь вверх"; законы физики одинаковы независимо от того, как вы ориентируетесь. Эта симметрия приводит к уравнению неразрывности для сохранение углового момента.

Видеть Теорема Нётер за доказательствами и подробностями.

Смотрите также

• Закон сохранения
• Форма сохранения
• Диссипативная система

Рекомендации

1. Педлоски, Джозеф (1987). Геофизическая гидродинамика. Springer. стр.10–13. ISBN  978-0-387-96387-7.
2. Клэнси, Л.Дж. (1975), Аэродинамика, Раздел 3.3, Pitman Publishing Limited, Лондон
3. Филдинг, Сюзанна. «Основы гидродинамики» (PDF). Даремский университет. Получено 22 декабря 2019.
4. Для этого вывода см., Например, МакМахон, Д. (2006). Демистификация квантовой механики. Макгроу Хилл. ISBN  0-07-145546-9.
5. Д. МакМахон (2006). Демистифицированная теория относительности. Макгроу Хилл (США). ISBN  0-07-145545-0.
6. C.W. Misner; К.С. Торн; J.A. Уиллер (1973). Гравитация. W.H. Freeman & Co. ISBN  0-7167-0344-0.
7. Майкл Вайс; Джон Баэз. "Сохраняется ли энергия в общей теории относительности?". Получено 2014-04-25.
8. J.A. Уиллер; К. Миснер; К.С. Торн (1973). Гравитация. W.H. Freeman & Co., стр. 558–559. ISBN  0-7167-0344-0.

дальнейшее чтение

• Гидродинамика, Х. Лэмб, Cambridge University Press, (оцифровка 6-го издания 1932 г., 2006 г.) ISBN  978-0-521-45868-9
• Введение в электродинамику (3-е издание), Д.Дж. Гриффитс, Pearson Education Inc, 1999 г., ISBN  81-7758-293-3
• Электромагнетизм (2-е издание), И.С. Грант, У. Р. Филлипс, Манчестерская физическая серия, 2008 г. ISBN  0-471-92712-0
• Гравитация, Дж. Уиллер, К. Миснер, К.С. Торн, W.H. Freeman & Co, 1973, ISBN  0-7167-0344-0