Вязкоупругость - Viscoelasticity
| Часть серии по | ||||
| Механика сплошной среды | ||||
|---|---|---|---|---|
Законы
| ||||
Вязкоупругость это свойство материалов, которые демонстрируют как вязкий и эластичный характеристики при прохождении деформация. Вязкие материалы, такие как вода, сопротивляются сдвиговый поток и напряжение линейно со временем, когда стресс применяется. Эластичные материалы деформируются при растяжении и сразу возвращаются в исходное состояние после снятия напряжения.
Вязкоупругие материалы обладают элементами обоих этих свойств и, как таковые, демонстрируют деформацию, зависящую от времени. В то время как эластичность обычно является результатом связь протягиваясь вдоль кристаллографические плоскости в упорядоченном твердом теле вязкость является результатом диффузии атомов или молекул внутри аморфный материал.[1]
Фон
В девятнадцатом веке такие физики, как Максвелл, Больцман, и Кельвин исследовал и экспериментировал с слизняк и восстановление очки, металлы, и каучуки. Вязкоупругость была дополнительно исследована в конце двадцатого века, когда синтетические полимеры были разработаны и использовались во множестве приложений.[2] Расчеты вязкоупругости сильно зависят от вязкость переменная, η. Обратное к η также известно как текучесть, φ. Значение любого из них может быть получено как функция температуры или как заданное значение (т.е. для приборная панель ).[1]
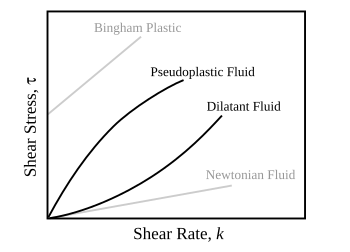
В зависимости от изменения скорости деформации в зависимости от напряжения внутри материала вязкость можно разделить на линейную, нелинейную или пластическую. Когда материал демонстрирует линейный отклик, он классифицируется как Ньютоновский материал. В этом случае напряжение линейно пропорционально скорости деформации. Если материал демонстрирует нелинейный отклик на скорость деформации, он классифицируется как Неньютоновская жидкость. Существует также интересный случай, когда вязкость уменьшается, поскольку скорость сдвига / деформации остается постоянной. Материал, который демонстрирует такое поведение, известен как тиксотропный. Кроме того, когда напряжение не зависит от этой скорости деформации, материал демонстрирует пластическую деформацию.[1] Многие вязкоупругие материалы демонстрируют резинка подобное поведение объясняется термодинамической теорией упругости полимера.
Некоторые примеры вязкоупругих материалов включают аморфные полимеры, полукристаллические полимеры, биополимеры, металлы при очень высоких температурах и битумные материалы. Растрескивание происходит, когда напряжение прикладывается быстро и за пределами предела упругости. Связки и сухожилия являются вязкоупругими, поэтому степень их потенциального повреждения зависит как от скорости изменения их длины, так и от приложенной силы.[нужна цитата ]
Вязкоупругий материал обладает следующими свойствами:
- гистерезис видно в кривая напряжение – деформация
- снятие стресса происходит: ступенчатая постоянная деформация вызывает уменьшение напряжения
- слизняк происходит: ступенька постоянное напряжение вызывает увеличение напряжения
- его жесткость зависит от скорость деформации или уровень стресса
Упругое и вязкоупругое поведение
В отличие от чисто эластичных веществ, вязкоупругое вещество имеет упругий компонент и вязкий компонент. В вязкость вязкоупругого вещества дает ему зависимость скорости деформации от времени. Чисто эластичные материалы не рассеивают энергию (тепло) при приложении, а затем снятии нагрузки. Однако вязкоупругое вещество рассеивает энергию при приложении нагрузки, а затем ее снятии. Гистерезис наблюдается на кривой деформирования, при этом площадь петли равна потерям энергии во время цикла нагружения. Поскольку вязкость - это сопротивление термически активированной пластической деформации, вязкий материал будет терять энергию в ходе цикла нагрузки. Пластическая деформация приводит к потерям энергии, что нехарактерно для реакции чисто упругого материала на цикл нагружения.[1]
В частности, вязкоупругость - это молекулярная перестройка. Когда напряжение прикладывается к вязкоупругому материалу, такому как полимер, части длинной полимерной цепи меняют положение. Это движение или перестановка называется слизняк. Полимеры остаются твердым материалом, даже когда эти части их цепей перестраиваются, чтобы сопровождать напряжение, и когда это происходит, это создает обратное напряжение в материале. Когда обратное напряжение имеет ту же величину, что и приложенное напряжение, материал больше не ползет. Когда исходное напряжение снимается, накопленные обратные напряжения заставят полимер вернуться к своей исходной форме. Материал ползет, что дает приставку вязко-, и материал полностью восстанавливается, что дает суффикс -эластичность.[2]
Типы
Линейная вязкоупругость когда функция отделяемый как в реакции на ползучесть, так и в нагрузке. Все линейные вязкоупругие модели можно представить в виде Уравнение Вольтерра соединение стресс и напряжение:
или же
куда
- т время
- является стресс
- является напряжение
- и мгновенно модули упругости для ползания и расслабления
- К (т) это слизняк функция
- F (т) функция релаксации
Линейная вязкоупругость обычно применима только для малых деформации.
Нелинейная вязкоупругость - это когда функция не отделима. Обычно это случается, когда деформации имеют большие размеры или если материал при деформациях меняет свои свойства.
An неэластичный Материал - это особый случай вязкоупругого материала: неупругий материал полностью восстанавливается до своего исходного состояния при снятии нагрузки.
Динамический модуль
Вязкоупругость изучается с помощью динамический механический анализ, прикладывая небольшое колебательное напряжение и измеряя результирующую деформацию.
- В чисто эластичных материалах напряжение и деформация совпадают по фазе, поэтому реакция одного на другое происходит мгновенно.
- В чисто вязких материалах деформация отстает от напряжения на фазу 90 градусов.
- Вязкоупругие материалы демонстрируют поведение где-то посередине этих двух типов материалов, демонстрируя некоторое отставание в деформации.
Комплекс динамический модуль G можно использовать для представления отношений между осциллирующим напряжением и деформацией:
куда ; это модуль упругости и это модуль потерь:
куда и - амплитуды напряжения и деформации соответственно, а - фазовый сдвиг между ними.
Учредительные модели линейной вязкоупругости

Вязкоупругие материалы, такие как аморфные полимеры, полукристаллические полимеры, биополимеры и даже живые ткани и клетки,[3] могут быть смоделированы для определения их взаимодействия напряжения и деформации или силы и смещения, а также их временных зависимостей. Эти модели, которые включают Модель Максвелла, то Модель Кельвина – Фойгта, то стандартная линейная твердотельная модель, а Модель Бюргерса, используются для прогнозирования реакции материала при различных условиях нагружения. Вязкоупругое поведение включает упругие и вязкие компоненты, моделируемые как линейные комбинации пружины и приборные панели, соответственно. Каждая модель отличается расположением этих элементов, и все эти вязкоупругие модели могут быть эквивалентно смоделированы как электрические цепи. В эквивалентной электрической цепи напряжение представлено током, а скорость деформации по напряжению. Модуль упругости пружины аналогичен модулю упругости цепи. емкость (он накапливает энергию) и вязкость демпфера для цепи сопротивление (рассеивает энергию).
Упругие компоненты, как упоминалось ранее, можно смоделировать как пружины упругой постоянной E по формуле:
где σ - напряжение, E - модуль упругости материала, а ε - деформация, возникающая при данном напряжении, аналогично Закон Гука.
Вязкие компоненты можно моделировать как приборные панели таким образом, что зависимость между напряжением и скоростью деформации может быть записана как,
где σ - напряжение, η - вязкость материала, а dε / dt - производная деформации по времени.
Связь между напряжением и деформацией может быть упрощена для конкретных скоростей напряжения или деформации. Для высоких скоростей напряжения или деформации / коротких периодов времени преобладают производные по времени компоненты зависимости напряжение-деформация. В этих условиях его можно представить как жесткий стержень, способный выдерживать высокие нагрузки без деформации. Следовательно, приборную панель можно рассматривать как "короткое замыкание".[4][5]
И наоборот, для состояний с низким напряжением / более длительных периодов времени компоненты производной по времени пренебрежимо малы, и контрольная точка может быть эффективно удалена из системы - «разомкнутая» цепь. [5]. В результате только пружина, подключенная параллельно к приборной панели, будет вносить вклад в общую нагрузку в системе.[4]
Модель Максвелла

Модель Максвелла может быть представлена чисто вязким демпфером и чисто упругой пружиной, соединенными последовательно, как показано на схеме. Модель может быть представлена следующим уравнением:
Согласно этой модели, если материал подвергается постоянной деформации, напряжения постепенно расслабляться. Когда материал подвергается постоянному напряжению, деформация состоит из двух компонентов. Во-первых, мгновенно возникает упругий компонент, соответствующий пружине, и сразу же расслабляется после снятия напряжения. Второй - это вязкий компонент, который со временем растет, пока действует напряжение. Модель Максвелла предсказывает, что напряжение экспоненциально спадает со временем, что верно для большинства полимеров. Одним из ограничений этой модели является то, что она не дает точного предсказания ползучести. Модель Максвелла для условий ползучести или постоянного напряжения постулирует, что деформация будет линейно увеличиваться со временем. Однако полимеры по большей части показывают, что скорость деформации со временем уменьшается.[2]
Области применения для мягких твердых тел: термопластические полимеры с температурой, близкой к их температуре плавления, свежий бетон (без учета его старения), многие металлы при температуре, близкой к их температуре плавления.
Модель Кельвина – Фойгта

Модель Кельвина – Фойгта, также известная как модель Фойгта, состоит из ньютоновского демпфера и упругой пружины Гука, соединенных параллельно, как показано на рисунке. Он используется для объяснения ползучести полимеров.
Материальное соотношение выражается в виде линейного дифференциального уравнения первого порядка:
Эта модель представляет собой твердое тело, подвергающееся обратимой вязкоупругой деформации. При приложении постоянного напряжения материал деформируется с уменьшающейся скоростью, асимптотически приближаясь к установившейся деформации. Когда напряжение снимается, материал постепенно расслабляется до недеформированного состояния. При постоянном напряжении (ползучести) модель вполне реалистична, поскольку она предсказывает, что деформация будет стремиться к σ / E по мере того, как время продолжается до бесконечности. Как и модель Максвелла, модель Кельвина – Фойгта также имеет ограничения. Модель очень хороша в моделировании ползучести материалов, но в отношении релаксации модель намного менее точна.[6]
Область применения: органические полимеры, резина, дерево при не слишком высоких нагрузках.
Стандартная линейная твердотельная модель
Стандартная линейная твердотельная модель, также известная как модель Зенера, состоит из двух пружин и демпфера. Это простейшая модель, которая правильно описывает как ползучесть, так и релаксацию напряжений вязкоупругого материала. Для этой модели определяющими определяющими отношениями являются:
| Представление Максвелла | Кельвин представление |
|---|---|
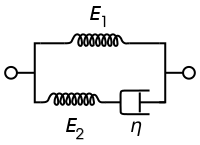 | 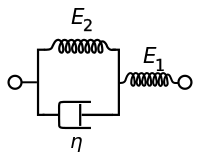 |
При постоянном напряжении моделируемый материал мгновенно деформируется до некоторой деформации, которая представляет собой мгновенную упругую часть деформации. После этого он будет продолжать деформироваться и асимптотически приближаться к установившейся деформации, которая представляет собой запаздывающую упругую часть деформации. Хотя Стандартная линейная твердотельная модель более точна, чем модели Максвелла и Кельвина – Фойгта в прогнозировании отклика материала, математически она дает неточные результаты для деформации при определенных условиях нагрузки.
Модель Бюргерса
Модель Бюргерса состоит либо из двух параллельно включенных компонентов Максвелла, либо из последовательно включенных компонентов Кельвина – Фойгта, пружины и датчика. Для этой модели определяющими определяющими отношениями являются:
| Представление Максвелла | Кельвин представление |
|---|---|
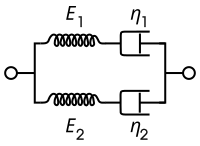 | 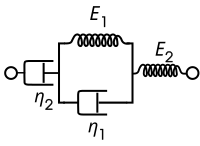 |
Эта модель включает вязкое течение в стандартную линейную твердотельную модель, давая линейно возрастающую асимптоту для деформации при фиксированных условиях нагружения.
Обобщенная модель Максвелла

Обобщенная модель Максвелла, также известная как модель Вихерта, является наиболее общей формой линейной модели вязкоупругости. При этом учитывается, что расслабление происходит не в один момент времени, а в разное время. Из-за того, что молекулярные сегменты разной длины, причем более короткие дают меньший вклад, чем более длинные, существует различное временное распределение. Модель Вихерта показывает это, имея столько элементов Максвелла, сколько необходимо для точного представления распределения. На рисунке справа показана обобщенная модель Вихерта.[7]Область применения: металлы и сплавы при температурах ниже четверти их абсолютной температуры плавления (выраженной в К).
Серия Прони
В одномерном испытании на релаксацию материал подвергается внезапной деформации, которая сохраняется постоянной в течение всего испытания, и напряжение измеряется с течением времени. Начальное напряжение возникает из-за упругого отклика материала. Затем со временем напряжение спадает из-за вязких эффектов в материале. Обычно применяется деформация растяжения, сжатия, объемного сжатия или сдвига. Полученные в результате данные зависимости напряжения от времени можно описать с помощью ряда уравнений, называемых моделями. В зависимости от типа приложенной деформации меняются только обозначения: релаксация растяжения-сжатия обозначается , shearis обозначается , объем обозначается . Серия Прони для релаксации сдвига:
куда длительный модуль упругости после полного расслабления материала, время релаксации (не путать с на схеме); чем выше их значения, тем больше времени требуется для снятия стресса. Данные подогнаны к уравнению с помощью алгоритма минимизации, который регулирует параметры (), чтобы минимизировать ошибку между прогнозируемым значением и значением данных.[8]
Альтернативная форма получена с учетом того, что модуль упругости связан с длительным модулем упругости соотношением
Следовательно,
Такая форма удобна, когда модуль упругости сдвига получается из данных, не зависящих от данных релаксации, и / или для компьютерной реализации, когда желательно указать упругие свойства отдельно от вязких свойств, как в.[9]
Эксперимент на ползучесть обычно легче выполнить, чем эксперимент на релаксацию, поэтому большинство данных доступно в виде зависимости (ползучести) податливости от времени.[10] К сожалению, нет известной закрытой формы для соответствия (ползучести) с точки зрения коэффициента Pronyseries. Таким образом, если есть данные о ползучести, непросто получить коэффициенты (релаксационного) ряда Прони, которые необходимы, например, в.[9] Целесообразный способ получения этих коэффициентов следующий. Во-первых, сопоставьте данные о ползучести с моделью, которая имеет решения в замкнутой форме как для соответствия, так и для ослабления; например, модель Максвелла-Кельвина (уравнение 7.18-7.19) в[11] или Стандартная твердотельная модель (ур. 7.20-7.21) в[11] (раздел 7.1.3). Как только параметры модели ползучести известны, сгенерируйте псевдоданные релаксации с помощью модели сопряженной релаксации для тех же времен, что и исходные данные. Наконец, сопоставьте псевдоданные с рядом Прони.
Влияние температуры на вязкоупругие свойства
Вторичные связи полимера постоянно разрушаются и преобразовываются из-за теплового движения. Приложение напряжения благоприятствует одним конформациям по сравнению с другими, поэтому молекулы полимера будут постепенно «перетекать» в предпочтительные конформации с течением времени.[12] Поскольку тепловое движение является одним из факторов, способствующих деформации полимеров, вязкоупругие свойства изменяются с повышением или понижением температуры. В большинстве случаев модуль ползучести, определяемый как отношение приложенного напряжения к зависящей от времени деформации, уменьшается с повышением температуры. Вообще говоря, повышение температуры коррелирует с логарифмическим уменьшением времени, необходимого для создания одинаковой деформации при постоянном напряжении. Другими словами, растяжение вязкоупругого материала на равное расстояние при более высокой температуре требует меньше работы, чем при более низкой температуре.
Более подробно влияние температуры на вязкоупругое поведение полимера можно изобразить, как показано.
В типичные полимеры входят в основном пять областей (некоторые обозначены как четыре, которые объединяют вместе VI и V).[13].
Область I: Стекловидное состояние полимера представлено в этой области. Температура в этой области для данного полимера слишком низкая, чтобы обеспечить движение молекул. Следовательно, движение молекул в этой области заморожено. Механические свойства в этой области твердые и хрупкие.[14].
Область II: в этой области полимер проходит температуру стеклования. За пределами Tg тепловой энергии, обеспечиваемой окружающей средой, достаточно, чтобы разморозить движение молекул. Молекулы могут иметь локальное движение в этой области, что приводит к резкому падению жесткости по сравнению с областью I.
Район III: Район каучукового плато. Материалы, лежащие в этой области, будут обладать большой эластичностью, обусловленной энтропией. Например, в исходном состоянии этой области неупорядочена резинка. Растягивая резинку, вы также выравниваете структуру, чтобы она была более упорядоченной. Следовательно, при отпускании резиновой ленты он самопроизвольно будет искать состояние с более высокой энтропией, а следовательно, возвращается в исходное состояние. Это то, что мы назвали восстановлением формы упругости за счет энтропии.
Область IV: поведение в области эластичного течения сильно зависит от времени. Полимеры в этой области должны использовать суперпозицию время-температура, чтобы получить более подробную информацию, чтобы осторожно решить, как использовать материалы. Например, если материал используется для решения задачи с коротким временем взаимодействия, он может быть «твердым». При использовании в целях длительного взаимодействия он будет действовать как «мягкий» материал.[15].
Область V: Вязкий полимер легко течет в этой области. Еще одно существенное падение жесткости.

Экстремальные низкие температуры могут привести к изменению вязкоупругих материалов на стекло фаза и стать хрупкий. Например, экспонирование чувствительные к давлению клеи до сильного холода (сухой лед, замораживающий спрей и т. д.) заставляет их терять липкость, что приводит к расслоению.
Вязкоупругая ползучесть
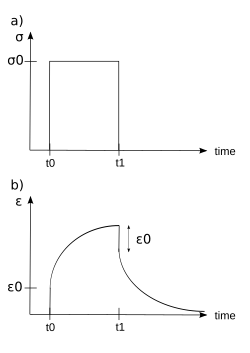
Под действием ступенчатого постоянного напряжения вязкоупругие материалы испытывают зависящее от времени увеличение деформации. Это явление известно как вязкоупругая ползучесть.
Вовремя , вязкоупругий материал нагружается постоянным напряжением, которое сохраняется в течение достаточно длительного периода времени. Материал реагирует на напряжение напряжением, которое увеличивается до тех пор, пока материал не разрушится, если это вязкоупругая жидкость. Если, с другой стороны, это вязкоупругое твердое тело, оно может или не может разрушиться, в зависимости от приложенного напряжения по сравнению с предельным сопротивлением материала. Когда напряжение сохраняется в течение более короткого периода времени, материал подвергается начальной деформации, пока не наступит время , после чего деформация сразу уменьшается (разрыв), затем постепенно уменьшается в разы до остаточного напряжения.
Данные вязкоупругой ползучести можно представить путем построения графика модуля ползучести (постоянное приложенное напряжение, деленное на общую деформацию в конкретный момент времени) как функцию времени.[16] Ниже критического напряжения модуль вязкоупругой ползучести не зависит от приложенного напряжения. Семейство кривых, описывающих зависимость деформации от времени на различные приложенные напряжения, может быть представлена одной кривой зависимости модуля вязкоупругой ползучести от времени, если приложенные напряжения ниже критического значения напряжения материала.
Вязкоупругая ползучесть важна при рассмотрении долгосрочного проектирования конструкций. Учитывая условия нагрузки и температуры, конструкторы могут выбрать материалы, которые лучше всего подходят для срока службы компонентов.
Измерение
Хотя существует множество инструментов, которые проверяют механическую и вязкоупругую реакцию материалов, широкополосная вязкоупругая спектроскопия (BVS) и резонансная ультразвуковая спектроскопия (RUS) чаще используются для испытания вязкоупругого поведения, поскольку они могут использоваться при температурах выше и ниже окружающей среды и более специфичны для испытания вязкоупругости. Эти два прибора используют демпфирующий механизм на различных частотах и временных диапазонах, не обращаясь к суперпозиция времени и температуры. Использование BVS и RUS для изучения механических свойств материалов важно для понимания того, как будет работать материал, демонстрирующий вязкоупругость.[17]
Смотрите также
Рекомендации
- ^ а б c d е Мейерс и Чавла (1999): «Механическое поведение материалов», 98-103.
- ^ а б c МакКрам, Бакли и Бакнелл (2003): «Принципы полимерной инженерии», 117-176.
- ^ Бисвас, Абхиджит; Manivannan, M .; Шринивасан, Мандьям А. (2015). "Многомасштабная слоистая биомеханическая модель тельца Пачинии". Транзакции IEEE по тактильности. 8 (1): 31–42. Дои:10.1109 / TOH.2014.2369416. PMID 25398182.
- ^ а б Ван Влит, Кристин Дж. (2006); «3.032 Механическое поведение материалов»
- ^ а б Какопардо, Людовика (январь 2019 г.). «Инженерная вязкоупругость гидрогеля». Журнал механического поведения биомедицинских материалов. 89: 162–167 - через Elsevier.
- ^ Таннер, Роджер И. (1988). Инжиниринг Реологу. Издательство Оксфордского университета. п. 27. ISBN 0-19-856197-0.
- ^ Ройланс, Дэвид (2001); «Инженерная вязкоупругость», 14-15
- ^ Э. Дж. Барберо. Принцип суперпозиции время-температура-возраст для прогнозирования долговременного отклика линейных вязкоупругих материалов, глава 2 книги Ползучесть и усталость композитов с полимерной матрицей. Вудхед, 2011.[1].
- ^ а б Симулия. Руководство пользователя Abaqus Analysis, 19.7.1 Викоупругость во временной области, издание 6.10, 2010 г.
- ^ Компьютерный предварительный отбор материалов по единым стандартам
- ^ а б Э. Дж. Барберо. Конечно-элементный анализ композиционных материалов. CRC Press, Бока-Ратон, Флорида, 2007. [2]
- ^ С.А. Баерле, А. Хотта, А.А. Гусев, Полимер 47, 6243-6253 (2006).
- ^ Aklonis., J.J. (1981). «Механические свойства полимера». J Chem Educ. 58:892.
- ^ И. М., Калогерас (2012). «Природа стеклообразного состояния: структура и стеклование». Журнал материаловедения образования. 34(3), 69.
- ^ Я, Эмри (2010). Поведение твердых полимеров в зависимости от времени.
- ^ Розато и др. (2001): «Справочник по дизайну пластмасс», 63-64.
- ^ Род Лейкс (1998). Вязкоупругие твердые тела. CRC Press. ISBN 0-8493-9658-1.
- Силби и Олберти (2001): Физическая химия, 857. John Wiley & Sons, Inc.
- Алан С. Уайнман и К. Р. Раджагопал (2000): Механический отклик полимеров: введение
- Аллен и Томас (1999): Структура материалов, 51.
- Crandal et al. (1999): Введение в механику твердого тела 348
- Ж. Леметр и Ж. Л. Шабош (1994) Механика твердых материалов
- Ю. Димитриенко (2011) Нелинейная механика сплошной среды и большие неупругие деформации, Springer, 772p





































![G (t) = G_0 - Sigma_ {i = 1} ^ {N} G_i [1- exp (-t / tau_i)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/75c0af1d0221bb0511fa5202f9af297b29299e38)



