Катеноид - Catenoid

Катеноид

Катеноид, полученный при вращении цепной линии.

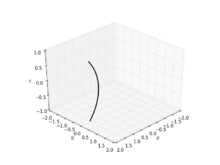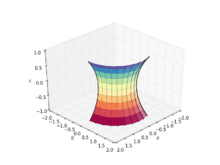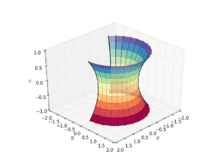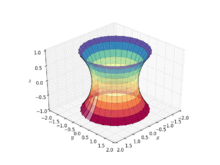
А катеноид это тип поверхности, возникающий при вращении цепная связь кривая вокруг оси.^[1] Это минимальная поверхность, что означает, что он занимает наименьшую площадь в замкнутом пространстве.^[2] Официально он был описан в 1744 году математиком Леонард Эйлер.

Мыльная пленка прикрепленные к двойным круглым кольцам, будут иметь форму катеноида.^[2] Потому что они члены одного и того же ассоциированная семья поверхностей катеноид можно согнуть в часть геликоид, наоборот.

Геометрия

Катеноид был первым нетривиальным минимальным поверхность в 3-мерном евклидовом пространстве, которое будет обнаружено помимо самолет. Катеноид получается путем вращения цепной цепи вокруг своей директриса.^[2] Он был найден и доказан Леонард Эйлер в 1744 г.^[3][4]

Ранние работы по этому вопросу были опубликованы также Жан Батист Менье.^[5][4]:11106 Есть только два минимальные поверхности вращения (поверхности вращения которые также являются минимальными поверхностями): самолет и катеноид.^[6]

Катеноид может быть определен следующими параметрическими уравнениями:

${\displaystyle x=c\cosh {\frac {v}{c}}\cos u}$

${\displaystyle y=c\cosh {\frac {v}{c}}\sin u}$

${\displaystyle z=v}$

куда ${\displaystyle u\in [-\pi ,\pi )}$ и ${\displaystyle v\in \mathbb {R} }$ и ${\displaystyle c}$ является ненулевой действительной константой.

В цилиндрических координатах:

${\displaystyle \rho =c\cosh {\frac {z}{c}}}$

куда ${\displaystyle c}$ это реальная константа.

Физическая модель катеноида может быть сформирована путем погружения двух круговой кольца в мыльный раствор и медленно раздвигая круги.

Катеноид также может быть приблизительно определен Метод растянутой сетки как фасетная 3D модель.

Преобразование геликоида

Деформация геликоид в катеноид

Потому что они члены одного и того же ассоциированная семья поверхностей, можно согнуть катеноид в часть геликоид без растяжения. Другими словами, можно (в основном) непрерывный и изометрический деформация катеноида на части геликоид так что каждый член семейства деформаций минимальный (иметь средняя кривизна нуля). А параметризация такой деформации задается системой

${\displaystyle x(u,v)=\cos \theta \,\sinh v\,\sin u+\sin \theta \,\cosh v\,\cos u}$

${\displaystyle y(u,v)=-\cos \theta \,\sinh v\,\cos u+\sin \theta \,\cosh v\,\sin u}$

${\displaystyle z(u,v)=u\cos \theta +v\sin \theta }$

за ${\displaystyle (u,v)\in (-\pi ,\pi ]\times (-\infty ,\infty )}$, с параметром деформации ${\displaystyle -\pi <\theta \leq \pi }$,

куда ${\displaystyle \theta =\pi }$ соответствует правому геликоиду, ${\displaystyle \theta =\pm \pi /2}$ соответствует катеноиду, а${\displaystyle \theta =0}$ соответствует левому геликоиду.

Рекомендации

1. Диркес, Ульрих; Хильдебрандт, Стефан; Совиньи, Фридрих (2010). Минимальные поверхности. Springer Science & Business Media. п. 141. ISBN  9783642116988.
2. Гуллберг, Ян (1997). Математика: от рождения чисел. W. W. Norton & Company. п.538. ISBN  9780393040029.
3. Helveticae, Euler, Leonhard (1952) [перепечатка издания 1744 года]. Каратеодори Константин (ред.). Methodus inveniendi lineas curvas: maximi minimive proprietate gaudentes sive solutio problematis isoperimetrici latissimo sensu acceptpti (на латыни). Springer Science & Business Media. ISBN  3-76431-424-9.
4. Colding, T. H .; Миникоцци, В. П. (17 июля 2006 г.). «Формы вложенных минимальных поверхностей». Труды Национальной академии наук. 103 (30): 11106–11111. Дои:10.1073 / pnas.0510379103. ЧВК  1544050. PMID  16847265.
5. Meusnier, J. B (1881). Mémoire sur la Courbure des поверхностей [Память о кривизне поверхностей.] (PDF) (На французском). Брюссель: Ф. Хайез, Imprimeur De L'Acdemie Royale De Belgique. С. 477–510. ISBN  9781147341744.
6. "Катеноид". Вольфрам MathWorld. Получено 15 января 2017.

дальнейшее чтение

• Кривошапко, Сергей; Иванов, В. Н. (2015). «Минимальные поверхности». Энциклопедия аналитических поверхностей. Springer. ISBN  9783319117737.

внешняя ссылка

• «Катеноид», Энциклопедия математики, EMS Press, 2001 [1994]
• Катеноид - модель WebGL
• Текст Эйлера, описывающий катеноид в Университете Карнеги-Меллона