Чувствительность и специфичность - Sensitivity and specificity

Чувствительность и специфичность

Чувствительность и специфичность статистические показатели эффективности двоичная классификация тест которые широко используются в медицине:

• Чувствительность измеряет долю правильно идентифицированных положительных результатов (например, процент больных, у которых правильно определено какое-либо заболевание).
• Специфика измеряет долю правильно идентифицированных негативов (например, процент здоровых людей, которые правильно определены как не болеющие).

Термины «положительный» и «отрицательный» относятся не к преимуществу, а к наличию или отсутствию состояния; например, если заболевание является заболеванием, «положительный» означает «больной», а «отрицательный» означает «здоровый».

Во многих тестах, в том числе диагностических медицинские анализы, чувствительность - это степень, в которой не упускаются из виду истинные положительные результаты, таким образом, количество ложных отрицательных результатов мало, а специфичность - это степень, в которой истинные отрицательные результаты классифицируются как таковые, таким образом, количество ложных положительных результатов невелико. Чувствительный тест редко упускает из виду истинный положительный результат (например, не показывает ничего неправильного, несмотря на наличие проблемы); конкретный тест редко регистрирует положительную классификацию чего-либо, что не является целью тестирования (например, обнаружение одного вида бактерий и принятие его за другой близкородственный, который является истинной целью).

Обычно существует компромисс между мерами. Например, в охрана аэропорта, поскольку тестирование пассажиров предназначено для выявления потенциальных угроз безопасности, сканеры могут быть настроены на включение сигналов тревоги на предметах с низким уровнем риска, таких как пряжки ремня и ключи (низкая специфичность), чтобы повысить вероятность идентификации опасных предметов и минимизировать риск пропуска предметов. которые действительно представляют угрозу (высокая чувствительность). Идеальный предсказатель будет на 100% чувствительным, то есть все больные будут правильно идентифицированы как больные, и на 100% специфичным, что означает, что ни один здоровый человек не будет неправильно идентифицирован как больной.

Термины «чувствительность» и «специфичность» были введены американским биостатистом Джейкобом Йерушалми в 1947 году.^[1]

Определения

В терминологии правда / ложно положительный / отрицательный, истинный или же ложный относится к присвоенной классификации, правильной или неправильной, в то время как положительный или же отрицательный относится к отнесению к положительной или отрицательной категории.

Терминология и производные
из матрица путаницы

положительное состояние (P) количество реальных положительных случаев в данных условие отрицательное (N) количество реальных отрицательных случаев в данных истинно положительный (TP) экв. с хитом истинно отрицательный (TN) экв. с правильным отклонением ложное срабатывание (FP) экв. с ложная тревога, Ошибка типа I ложноотрицательный (FN) экв. с мисс, Ошибка типа II чувствительность, отзывать, частота попаданий, или же истинно положительная ставка (TPR) ${displaystyle mathrm {TPR} ={frac {mathrm {TP} }{mathrm {P} }}={frac {mathrm {TP} }{mathrm {TP} +mathrm {FN} }}=1-mathrm {FNR} }$ специфичность, избирательность или же истинно отрицательная ставка (TNR) ${displaystyle mathrm {TNR} ={frac {mathrm {TN} }{mathrm {N} }}={frac {mathrm {TN} }{mathrm {TN} +mathrm {FP} }}=1-mathrm {FPR} }$ точность или же положительная прогностическая ценность (PPV) ${displaystyle mathrm {PPV} ={frac {mathrm {TP} }{mathrm {TP} +mathrm {FP} }}=1-mathrm {FDR} }$ отрицательная прогностическая ценность (ЧПС) ${displaystyle mathrm {NPV} ={frac {mathrm {TN} }{mathrm {TN} +mathrm {FN} }}=1-mathrm {FOR} }$ рейтинг промахов или ложноотрицательная ставка (FNR) ${displaystyle mathrm {FNR} ={frac {mathrm {FN} }{mathrm {P} }}={frac {mathrm {FN} }{mathrm {FN} +mathrm {TP} }}=1-mathrm {TPR} }$ выпадать или же ложноположительный рейтинг (FPR) ${displaystyle mathrm {FPR} ={frac {mathrm {FP} }{mathrm {N} }}={frac {mathrm {FP} }{mathrm {FP} +mathrm {TN} }}=1-mathrm {TNR} }$ коэффициент ложного обнаружения (FDR) ${displaystyle mathrm {FDR} ={frac {mathrm {FP} }{mathrm {FP} +mathrm {TP} }}=1-mathrm {PPV} }$ коэффициент ложных пропусков (ЗА) ${displaystyle mathrm {FOR} ={frac {mathrm {FN} }{mathrm {FN} +mathrm {TN} }}=1-mathrm {NPV} }$ Порог распространенности (PT) ${displaystyle PT={frac {{sqrt {TPR(-TNR+1)}}+TNR-1}{(TPR+TNR-1)}}}$ Оценка угрозы (TS) или индекс критического успеха (CSI) ${displaystyle mathrm {TS} ={frac {mathrm {TP} }{mathrm {TP} +mathrm {FN} +mathrm {FP} }}}$ точность (АКК) ${displaystyle mathrm {ACC} ={frac {mathrm {TP} +mathrm {TN} }{mathrm {P} +mathrm {N} }}={frac {mathrm {TP} +mathrm {TN} }{mathrm {TP} +mathrm {TN} +mathrm {FP} +mathrm {FN} }}}$ сбалансированная точность (BA) ${displaystyle mathrm {BA} ={frac {TPR+TNR}{2}}}$ Оценка F1 это гармоническое среднее из точность и чувствительность ${displaystyle mathrm {F} _{1}=2cdot {frac {mathrm {PPV} cdot mathrm {TPR} }{mathrm {PPV} +mathrm {TPR} }}={frac {2mathrm {TP} }{2mathrm {TP} +mathrm {FP} +mathrm {FN} }}}$ Коэффициент корреляции Мэтьюза (MCC) ${displaystyle mathrm {MCC} ={frac {mathrm {TP} imes mathrm {TN} -mathrm {FP} imes mathrm {FN} }{sqrt {(mathrm {TP} +mathrm {FP} )(mathrm {TP} +mathrm {FN} )(mathrm {TN} +mathrm {FP} )(mathrm {TN} +mathrm {FN} )}}}}$ Индекс Фаулкса – Маллоуса (FM) ${displaystyle mathrm {FM} ={sqrt {{frac {TP}{TP+FP}}cdot {frac {TP}{TP+FN}}}}={sqrt {PPVcdot TPR}}}$ информированность или букмекерской конторы (BM) ${displaystyle mathrm {BM} =mathrm {TPR} +mathrm {TNR} -1}$ отмеченность (МК) или deltaP ${displaystyle mathrm {MK} =mathrm {PPV} +mathrm {NPV} -1}$ Источники: Fawcett (2006),[2] Полномочия (2011),[3] Тинг (2011),[4], CAWCR[5] Д. Чикко и Г. Джурман (2020),[6] Тарват (2018).[7]

Заявка на отборочное исследование

Представьте себе исследование, оценивающее тест, который проверяет людей на наличие болезни. Каждый человек, проходящий тест, болеет или не болеет. Результат теста может быть положительным (классифицируя человека как больного) или отрицательным (классифицируя человека как не болеющего). Результаты тестирования по каждому предмету могут совпадать, а могут и не соответствовать его фактическому статусу. В этой обстановке:

• Истинно положительный результат: больные люди правильно определены как больные
• Ложноположительный результат: здоровые люди неправильно определены как больные
• Истинно отрицательный: здоровые люди правильно определены как здоровые
• Ложноотрицательный: больные люди, ошибочно идентифицированные как здоровые

Матрица путаницы

Рассмотрим группу с п положительные примеры и N отрицательные примеры некоторого состояния. Четыре исхода можно сформулировать в виде 2 × 2 Таблица сопряженности или же матрица путаницы, следующее:

		Истинное состояние
	Всего населения	Состояние положительное	Состояние отрицательное	Распространенность = Σ Условие положительное/Σ Всего населения	Точность (АКК) = Σ Истинно положительный + Σ Истинно отрицательный/Σ Всего населения
Прогнозируемое состояние	Прогнозируемое состояние положительный	Истинно положительный	Ложный положительный результат, Ошибка типа I	Положительная прогностическая ценность (PPV), Точность = Σ Истинно положительный/Σ Прогнозируемое состояние положительное	Уровень ложного обнаружения (FDR) = Σ Ложноположительный/Σ Прогнозируемое состояние положительное
	Прогнозируемое состояние отрицательный	Ложноотрицательный, Ошибка типа II	Правда отрицательный	Уровень ложных пропусков (ДЛЯ) = Σ Ложноотрицательный/Σ Прогнозируемое состояние отрицательное	Отрицательная прогностическая ценность (ЧПС) = Σ Истинно отрицательный/Σ Прогнозируемое состояние отрицательное
		Истинно положительная оценка (TPR), Отзывать, Чувствительность, вероятность обнаружения, Мощность = Σ Истинно положительный/Σ Условие положительное	Ложноположительная ставка (FPR), Выпадать, вероятность ложной тревоги = Σ Ложноположительный/Σ Условие отрицательное	Отношение положительного правдоподобия (LR +) = TPR/FPR	Соотношение диагностических шансов (DOR) = LR +/LR−	F1 счет = 2 · Точность · Отзыв/Точность + отзыв
		Ложноотрицательная ставка (FNR), Рейтинг промахов = Σ Ложноотрицательный/Σ Условие положительное	Специфика (SPC), селективность, Истинная отрицательная ставка (TNR) = Σ Истинно отрицательный/Σ Условие отрицательное	Отрицательное отношение правдоподобия (LR-) = FNR/TNR

Чувствительность

Рассмотрим на примере медицинского теста для диагностики заболевания. Чувствительность относится к способности теста правильно определять больных, у которых действительно есть данное состояние.^[8] В примере с медицинским тестом, используемым для выявления заболевания, чувствительность (иногда также называемая степенью выявления в клинических условиях) теста - это доля людей, у которых положительный результат теста на заболевание, среди тех, у кого есть болезнь. Математически это можно выразить как:

${displaystyle {egin{aligned}{ ext{sensitivity}}&={frac { ext{number of true positives}}{{ ext{number of true positives}}+{ ext{number of false negatives}}}}[8pt]&={frac { ext{number of true positives}}{ ext{total number of sick individuals in population}}}[8pt]&={ ext{probability of a positive test given that the patient has the disease}}end{aligned}}}$

Отрицательный результат теста с высокой чувствительностью полезен для исключения болезни.^[8] Тест с высокой чувствительностью является надежным, если его результат отрицательный, поскольку он редко ставит неправильный диагноз тем, у кого есть болезнь. Тест со 100% чувствительностью распознает всех пациентов с заболеванием по положительному результату. Отрицательный результат теста окончательно исключать наличие заболевания у пациента. Тем не менее, положительный результат теста с высокой чувствительностью не обязательно полезен для определения болезни. Предположим, что «поддельный» тестовый набор всегда дает положительный результат. При использовании на больных пациентах все пациенты дают положительный результат, что дает 100% чувствительность теста. Однако чувствительность не учитывает ложные срабатывания. Фальшивый тест также дает положительный результат у всех здоровых пациентов, что дает ему 100% ложноположительный результат, что делает его бесполезным для обнаружения или «управления» заболеванием.

Чувствительность не такая, как у точность или же положительная прогностическая ценность (отношение истинных положительных результатов к совокупным истинным и ложным положительным результатам), что является таким же утверждением о доле фактических положительных результатов в тестируемой популяции, чем о самом тесте.

При расчете чувствительности не учитываются неопределенные результаты теста. Если тест не может быть повторен, неопределенные образцы должны быть либо исключены из анализа (количество исключений должно быть указано при цитировании чувствительности), либо могут рассматриваться как ложноотрицательные (что дает наихудшее значение чувствительности и поэтому может недооценивать его).

Специфика

Рассмотрим на примере медицинского теста для диагностики заболевания. Специфика относится к способности теста правильно отклонять здоровых пациентов без каких-либо заболеваний. Специфичность теста - это доля здоровых пациентов, у которых известно, что у них нет заболевания, у которых результат теста будет отрицательным. Математически это также можно записать как:

${displaystyle {egin{aligned}{ ext{specificity}}&={frac { ext{number of true negatives}}{{ ext{number of true negatives}}+{ ext{number of false positives}}}}[8pt]&={frac { ext{number of true negatives}}{ ext{total number of well individuals in population}}}[8pt]&={ ext{probability of a negative test given that the patient is well}}end{aligned}}}$

Положительный результат теста с высокой специфичностью полезен для определения болезни. У здоровых пациентов тест редко дает положительные результаты. Положительный результат говорит о высокой вероятности наличия заболевания.^[9]

Тест с более высокой специфичностью имеет более низкую частоту ошибок типа I.

Графическая иллюстрация

• 

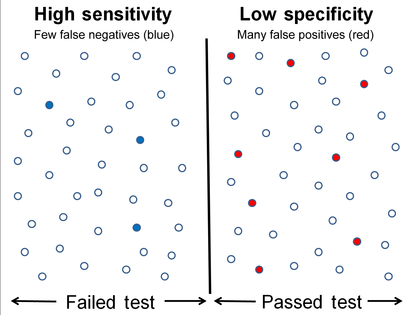
  Высокая чувствительность и низкая специфичность

• 

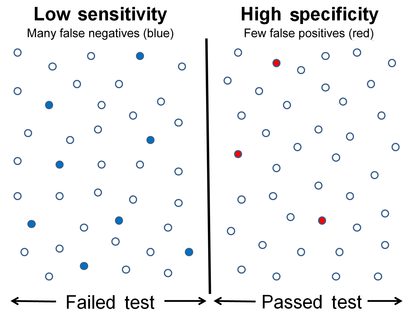
  Низкая чувствительность и высокая специфичность

Медицинские примеры

В медицинский диагноз, чувствительность теста - это способность теста правильно идентифицировать людей с заболеванием (истинно положительный показатель), тогда как специфичность теста - это способность теста правильно определять тех, у кого нет заболевания (истинно отрицательный показатель). на заболевание были протестированы, и 43 теста положительны, значит тест имеет чувствительность 43%. Если 100 тестируются без заболевания, а 96 дают полностью отрицательный результат, то специфичность теста 96%. Чувствительность и специфичность являются независимыми от распространенности характеристиками теста, поскольку их значения присущи самому тесту и не зависят от распространенности заболевания в интересующей популяции.^[10] Положительные и отрицательные прогностические значения, но не чувствительность или специфичность, являются значениями, на которые влияет распространенность болезни в тестируемой популяции. Эти концепции проиллюстрированы графически в этом апплете. Байесовская клиническая диагностическая модель которые показывают положительную и отрицательную прогностическую ценность в зависимости от распространенности, чувствительности и специфичности.

Порог распространенности

Взаимосвязь между прогностической ценностью положительного скринингового теста и его целевой распространенностью пропорциональна - хотя и не линейна во всех случаях, кроме одного особого случая. Следовательно, существует точка локальных экстремумов и максимальной кривизны, определяемая только как функция чувствительности и специфичности, за пределами которой скорость изменения прогностической ценности положительного теста падает с разной скоростью относительно распространенности заболевания. Эта точка была впервые определена с помощью дифференциальных уравнений Balayla et al. ^[11] и называется порог распространенности (${displaystyle phi _{e}}$). Уравнение для порога распространенности дается следующей формулой, где a = чувствительность и b = специфичность:

${displaystyle phi _{e}={frac {{sqrt {a(-b+1)}}+b-1}{(a+b-1)}}}$

Расположение этой точки на кривой скрининга имеет решающее значение для клиницистов и интерпретации положительных результатов скрининговых тестов в режиме реального времени.

Заблуждения

Часто утверждают, что высокоспецифичный тест эффективен для определения заболевания, если он положительный, в то время как высокочувствительный тест считается эффективным для исключения болезни, если он отрицательный.^[12][13] Это привело к появлению широко используемых мнемоник SPPIN и SNNOUT, согласно которым зрспециальный тест, когда пositive, правила в болезнь (SP-P-IN), и очень 'sепситивный тест, когда потводные правила из болезнь (SN-N-OUT). Однако оба практических правила вводят в заблуждение, поскольку диагностическая сила любого теста определяется как его чувствительностью. и его специфика.^[14][15][16]

Компромисс между специфичностью и чувствительностью исследуется в ROC анализ как компромисс между TPR и FPR (то есть отзывами и последствиями).^[17] Придание им равного веса оптимизирует информированность = специфичность + чувствительность-1 = TPR-FPR, величина которой дает вероятность принятия информированного решения между двумя классами (> 0 представляет надлежащее использование информации, 0 представляет эффективность на уровне вероятности, <0 представляет неправильное использование информации) .^[18]

Индекс чувствительности

В индекс чувствительности или же d ' (произносится как "ди-прайм") статистика используется в сигнале теория обнаружения. Он обеспечивает разделение между средними значениями распределения сигнала и шума по сравнению со стандартным отклонением распределения шума. За нормально распределенный сигнал и шум со средним и стандартным отклонениями ${displaystyle mu _{S}}$ и ${displaystyle sigma _{S}}$, и ${displaystyle mu _{N}}$ и ${displaystyle sigma _{N}}$соответственно, d 'определяется как:

${displaystyle d'={frac {mu _{S}-mu _{N}}{sqrt {{frac {1}{2}}(sigma _{S}^{2}+sigma _{N}^{2})}}}}$ ^[19]

Оценка d 'также может быть получена из измерений частоты совпадений и ложная тревога ставка. Он рассчитывается как:

d ' = Z(процент попаданий) - Z(частота ложных тревог),^[20]

где функция Z(п), п ∈ [0,1], является обратным кумулятивное распределение Гаусса.

d ' это безразмерный статистика. Высшее d ' указывает, что сигнал может быть более легко обнаружен.

Пример работы

• Посмотреть
• разговаривать
• редактировать

Рабочий пример

Диагностический тест с чувствительностью 67% и специфичностью 91% применяется к 2030 человек для поиска заболевания с распространенностью в популяции 1,48%.

		Пациенты с рак кишечника (как подтверждено на эндоскопия )
		Состояние положительное	Состояние отрицательное	Распространенность = (TP + FN) / Total_Population = (20+10)/2030 ≈1.48%	Точность (АКК) = (TP + TN) / Total_Population = (20+1820)/2030 ≈90.64%
Фекальный оккультизм кровь экран тест исход	Тест исход положительный	Истинно положительный (TP) = 20 (2030 х 1,48% х 67%)	Ложный положительный результат (FP) = 180 (2030 х (100 - 1,48%) х (100 - 91%))	Положительная прогностическая ценность (PPV), Точность = TP / (TP + FP) = 20 / (20 + 180) = 10%	Уровень ложного обнаружения (FDR) = FP / (TP + FP) = 180/(20+180) = 90.0%
	Тест исход отрицательный	Ложноотрицательный (FN) = 10 (2030 х 1,48% х (100 - 67%))	Правда отрицательный (TN) = 1820 (2030 х (100 -1,48%) х 91%)	Уровень ложных пропусков (ЗА) = FN / (FN + TN) = 10 / (10 + 1820) ≈ 0.55%	Отрицательная прогностическая ценность (ЧПС) = TN / (FN + TN) = 1820 / (10 + 1820) ≈ 99.45%
		TPR, Отзывать, Чувствительность = TP / (TP + FN) = 20 / (20 + 10) ≈ 66.7%	Ложноположительная ставка (FPR),Выпадать, вероятность ложной тревоги = FP / (FP + TN) = 180/(180+1820) =9.0%	Отношение положительного правдоподобия (LR +) = TPR/FPR = (20/30)/(180/2000) ≈7.41	Соотношение диагностических шансов (DOR) = LR +/LR− ≈20.2	F1 счет = 2 · Точность · Отзыв/Точность + отзыв ≈0.174
		Ложноотрицательная ставка (FNR), Рейтинг промахов = FN / (TP + FN) = 10/(20+10) ≈ 33.3%	Специфика, Избирательность, Истинная отрицательная ставка (TNR) = TN / (FP + TN) = 1820 / (180 + 1820) = 91%	Отрицательное отношение правдоподобия (LR-) = FNR/TNR = (10/30)/(1820/2000) ≈0.366

Связанные расчеты

• Уровень ложных срабатываний (α) = ошибка типа I = 1 - специфичность = FP / (FP + TN) = 180 / (180 + 1820) = 9%
• Ложноотрицательная ставка (β) = ошибка типа II = 1 - чувствительность = FN / (TP + FN) = 10 / (20 + 10) = 33%
• Мощность = чувствительность = 1 - β
• Отношение правдоподобия положительный = чувствительность / (1 - специфичность) = 0,67 / (1 - 0,91) = 7,4
• Отрицательное отношение правдоподобия = (1 - чувствительность) / специфичность = (1 - 0,67) / 0,91 = 0,37
• Порог распространенности = ${displaystyle PT={frac {{sqrt {TPR(-TNR+1)}}+TNR-1}{(TPR+TNR-1)}}}$ = 0.19 => 19.1%

Этот гипотетический скрининговый тест (анализ кала на скрытую кровь) правильно идентифицировал две трети (66,7%) пациентов с колоректальным раком.^[а] К сожалению, учет показателей распространенности показывает, что этот гипотетический тест имеет высокий уровень ложноположительных результатов и не позволяет надежно идентифицировать рак прямой кишки в общей популяции бессимптомных людей (PPV = 10%).

С другой стороны, этот гипотетический тест демонстрирует очень точное определение людей, свободных от рака (NPV = 99,5%). Следовательно, при использовании для рутинного скрининга колоректального рака у бессимптомных взрослых отрицательный результат дает важные данные для пациента и врача, например, исключение рака как причины желудочно-кишечных симптомов или успокаивание пациентов, обеспокоенных развитием колоректального рака.

Оценка ошибок в указанной чувствительности или специфичности

Сами по себе значения чувствительности и специфичности могут вводить в заблуждение. Необходимо рассчитать чувствительность или специфичность «наихудшего случая», чтобы не полагаться на эксперименты с небольшим количеством результатов. Например, конкретный тест может легко показать 100% чувствительность, если тестируется по золотому стандарту четыре раза, но один дополнительный тест по золотому стандарту, который дал плохой результат, будет означать чувствительность только 80%. Обычный способ сделать это - указать доверительный интервал биномиальной пропорции, часто рассчитывается с использованием интервала оценок Вильсона.

Доверительные интервалы чувствительность и специфичность можно рассчитать, указав диапазон значений, в котором правильное значение находится на заданном уровне достоверности (например, 95%).^[23]

Терминология в поиске информации

В поиск информации, положительная прогностическая ценность называется точность, а чувствительность называется отзывать. В отличие от компромисса между специфичностью и чувствительностью, эти меры не зависят от количества истинных негативов, которое обычно неизвестно и намного превышает фактическое количество релевантных и извлеченных документов. Это предположение об очень большом количестве истинно отрицательных по сравнению с положительными редко встречается в других приложениях.^[18]

В F-оценка может использоваться как единичный критерий выполнения теста для положительного класса. F-оценка - это гармоническое среднее точности и отзывчивости:

${displaystyle F=2 imes {frac {{ ext{precision}} imes { ext{recall}}}{{ ext{precision}}+{ ext{recall}}}}}$

На традиционном языке статистическая проверка гипотез, чувствительность теста называется статистическая мощность теста, хотя слово мощность в этом контексте имеет более общее использование, которое не применимо в данном контексте. У чувствительного теста будет меньше Ошибки типа II.

Смотрите также

• Научный портал
• Биологический портал
• Портал медицины

• Оценка Бриера
• Кумулятивный профиль точности
• Ложноположительный парадокс
• Дискриминация
• Точность и отзыв
• Статистическая значимость
• Коэффициент неопределенности, также называемый мастерством
• Статистика Юдена J

Примечания

1. У всех медицинских скрининговых тестов есть свои преимущества и недостатки. Рекомендации по клинической практике, например, для скрининга колоректального рака, опишите эти риски и преимущества.^[21][22]

Рекомендации

1. Ерушалмы Ж (1947). «Статистические проблемы оценки методов медицинской диагностики с особым упором на рентгенологические методы». Отчеты общественного здравоохранения. 62 (2): 1432–39. Дои:10.2307/4586294. JSTOR  4586294. PMID  20340527.
2. Фосетт, Том (2006). «Введение в ROC-анализ» (PDF). Письма с распознаванием образов. 27 (8): 861–874. Дои:10.1016 / j.patrec.2005.10.010.
3. Пауэрс, Дэвид М. В. (2011). «Оценка: от точности, отзыва и F-меры к ROC, информированности, значимости и корреляции». Журнал технологий машинного обучения. 2 (1): 37–63.
4. Тинг, Кай Мин (2011). Саммут, Клод; Уэбб, Джеффри I (ред.). Энциклопедия машинного обучения. Springer. Дои:10.1007/978-0-387-30164-8. ISBN  978-0-387-30164-8.
5. Брукс, Гарольд; Браун, Барб; Эберт, Бет; Ферро, Крис; Джоллифф, Ян; Ко, Тие-Йонг; Роббер, Пол; Стивенсон, Дэвид (26 января 2015 г.). «Совместная рабочая группа ВПМИ / РГЧЭ по исследованиям для проверки прогнозов». Сотрудничество в области исследований погоды и климата Австралии. Всемирная метеорологическая организация. Получено 2019-07-17.
6. Chicco D, Jurman G (январь 2020 г.). «Преимущества коэффициента корреляции Мэтьюза (MCC) над оценкой F1 и точность оценки бинарной классификации». BMC Genomics. 21 (1): 6-1–6-13. Дои:10.1186 / s12864-019-6413-7. ЧВК  6941312. PMID  31898477.
7. Тарват А. (август 2018 г.). «Классификационные методы оценки». Прикладные вычисления и информатика. Дои:10.1016 / j.aci.2018.08.003.
8. Альтман Д.Г., Бланд Дж. М. (июнь 1994 г.). «Диагностические тесты. 1: Чувствительность и специфичность». BMJ. 308 (6943): 1552. Дои:10.1136 / bmj.308.6943.1552. ЧВК  2540489. PMID  8019315.
9. «SpPins и SnNout». Центр доказательной медицины (CEBM). Получено 26 декабря 2013.
10. Мангрулкар Р. «Диагностическое обоснование I и II». Получено 24 января 2012.
11. Балайла, Жак.«Порог распространенности и геометрия скрининговых кривых». Препринт arXiv arXiv: 2006.00398 (2020).
12. «Доказательная диагностика». Университет штата Мичиган. Архивировано из оригинал на 2013-07-06. Получено 2013-08-23.
13. «Чувствительность и специфичность». Курс доказательной медицины медицинского факультета Университета Эмори.
14. Барон Дж. А. (апрель – июнь 1994 г.). «Жаль, что это неправда». Принятие медицинских решений. 14 (2): 107. Дои:10.1177 / 0272989X9401400202. PMID  8028462. S2CID  44505648.
15. Бойко Е.Ю. (апрель – июнь 1994 г.). «Исключение или устранение болезни с помощью наиболее чувствительного или специфического диагностического теста: короткий путь или неверный поворот?». Принятие медицинских решений. 14 (2): 175–9. Дои:10.1177 / 0272989X9401400210. PMID  8028470. S2CID  31400167.
16. Pewsner D, Battaglia M, Minder C, Marx A, Bucher HC, Egger M (июль 2004 г.). «Постановка диагноза с помощью« SpPIn »и« SnNOut »: предупреждение». BMJ. 329 (7459): 209–13. Дои:10.1136 / bmj.329.7459.209. ЧВК  487735. PMID  15271832.
17. Фосетт, Том (2006). «Введение в ROC-анализ». Письма с распознаванием образов. 27 (8): 861–874. Дои:10.1016 / j.patrec.2005.10.010.
18. Пауэрс, Дэвид М. В. (2011). «Оценка: от точности, отзыва и F-меры к ROC, информированности, значимости и корреляции». Журнал технологий машинного обучения. 2 (1): 37–63. HDL:2328/27165.
19. Гейл С.Д., Перкель ди-джей (январь 2010 г.). «Путь базальных ганглиев управляет избирательными слуховыми реакциями в дофаминергических нейронах певчих птиц посредством растормаживания». Журнал неврологии. 30 (3): 1027–37. Дои:10.1523 / JNEUROSCI.3585-09.2010. ЧВК  2824341. PMID  20089911.
20. Macmillan NA, Creelman CD (15 сентября 2004 г.). Теория обнаружения: руководство пользователя. Психология Press. п. 7. ISBN  978-1-4106-1114-7.
21. Лин, Дженнифер С .; Пайпер, Маргарет А .; Perdue, Лесли А .; Раттер, Кэролайн М .; Уэббер, Элизабет М .; О’Коннор, Элизабет; Смит, Нин; Уитлок, Эвелин П. (21 июня 2016 г.). «Скрининг колоректального рака». JAMA. 315 (23): 2576–2594. Дои:10.1001 / jama.2016.3332. ISSN  0098-7484.
22. Бенар, Флоренция; Баркун, Алан Н .; Мартель, Мириам; Рентельн, Даниэль фон (7 января 2018 г.). «Систематический обзор рекомендаций по скринингу на рак прямой кишки для взрослых со средним риском: обобщение текущих глобальных рекомендаций». Всемирный журнал гастроэнтерологии. 24 (1): 124–138. Дои:10.3748 / wjg.v24.i1.124. ЧВК  5757117. PMID  29358889.
23. «Онлайн-калькулятор диагностического теста вычисляет чувствительность, специфичность, отношения правдоподобия и прогнозные значения из таблицы 2x2 - калькулятора доверительных интервалов для прогнозных параметров». medcalc.org.

дальнейшее чтение

• Альтман Д.Г., Бланд Дж. М. (июнь 1994 г.). «Диагностические тесты. 1: Чувствительность и специфичность». BMJ. 308 (6943): 1552. Дои:10.1136 / bmj.308.6943.1552. ЧВК  2540489. PMID  8019315.
• Loong TW (сентябрь 2003 г.). «Понимание чувствительности и специфичности с помощью правого полушария мозга». BMJ. 327 (7417): 716–9. Дои:10.1136 / bmj.327.7417.716. ЧВК  200804. PMID  14512479.

внешняя ссылка

• Калькулятор UIC
• Калькулятор чувствительности / специфичности Vassar College
• Бесплатный онлайн-калькулятор MedCalc
• Апплет байесовской модели клинической диагностики