Белковый дизайн - Protein design

Эта статья о рациональном дизайне белков. Для более широкой инженерии белков см. Белковая инженерия.

Белковый дизайн это рациональный дизайн новых белок молекулы для разработки новой активности, поведения или цели, а также для углубления базового понимания функции белков.^[1] Белки можно создавать с нуля (de novo дизайн) или путем создания расчетных вариантов известной структуры белка и его последовательности (называемых редизайн белка). Рациональный дизайн белка подходы делают предсказания белковых последовательностей, которые складываются в конкретные структуры. Эти предсказанные последовательности могут быть затем подтверждены экспериментально с помощью таких методов, как пептидный синтез, сайт-направленный мутагенез, или же искусственный синтез генов.

Рациональный дизайн белков восходит к середине 1970-х годов.^[2] Однако в последнее время появилось множество примеров успешного рационального дизайна водорастворимых и даже трансмембранных пептидов и белков, отчасти благодаря лучшему пониманию различных факторов, способствующих стабильность структуры белка и разработка более совершенных вычислительных методов.

Обзор и история

Цель рационального белкового дизайна - предсказать аминокислота последовательности что будет складывать к определенной структуре белка. Хотя количество возможных белковых последовательностей огромно и экспоненциально растет с размером белковой цепи, только часть из них надежно и быстро сворачивается в одну. родное государство. Дизайн белка включает идентификацию новых последовательностей в этом подмножестве. Нативное состояние белка - это конформационная свободная энергия минимум для цепочки. Таким образом, дизайн белка - это поиск последовательностей, имеющих выбранную структуру как минимум свободной энергии. В некотором смысле это обратное предсказание структуры белка. В дизайне третичная структура указывается, и определяется последовательность, которая будет сворачиваться к нему. Следовательно, его также называют обратное складывание. В таком случае дизайн белка представляет собой проблему оптимизации: с использованием некоторых критериев оценки выбирается оптимизированная последовательность, которая будет сворачиваться до желаемой структуры.

Когда первые белки были рационально сконструированы в течение 1970-х и 1980-х годов, их последовательность была оптимизирована вручную на основе анализа других известных белков, состава последовательности, зарядов аминокислот и геометрии желаемой структуры.^[2] Первые разработанные белки приписываются Бернду Гутте, который разработал уменьшенную версию известного катализатора, бычьей рибонуклеазы и третичных структур, состоящих из бета-листов и альфа-спиралей, включая связующее вещество ДДТ. Урри и его коллеги позже разработали эластин -подобно волокнистый пептиды на основе правил композиции последовательностей. Ричардсон и его коллеги разработали белок из 79 остатков, не имеющий гомологии последовательности с известным белком.^[2] В 1990-х годах появление мощных компьютеров, библиотеки конформаций аминокислот, а силовые поля развиваются в основном для молекулярная динамика Моделирование позволило разработать инструменты для построения вычислительных белков на основе структур. После разработки этих вычислительных инструментов за последние 30 лет был достигнут большой успех в дизайне белков. Первый белок, успешно разработанный полностью de novo было сделано Стивен Мэйо и коллег в 1997 году,^[3] и вскоре после этого в 1999 г. Питер С. Ким и соавторы разработали димеры, тримеры и тетрамеры неестественных правосторонних спиральные катушки.^[4][5] В 2003 г. Дэвид Бейкер Лаборатория разработала полноценный белок в такой степени, которую раньше не было в природе.^[6] Позже, в 2008 году, группа Бейкера разработала компьютерные ферменты для двух разных реакций.^[7] В 2010 году одно из самых мощных нейтрализующих антител широкого спектра действия было выделено из сыворотки крови пациента с помощью белкового зонда, разработанного с помощью вычислений.^[8] Благодаря этим и другим успехам (например, см. Примеры ниже), белковый дизайн стал одним из самых важных инструментов, доступных для белковая инженерия. Есть большая надежда, что дизайн новых белков, больших и малых, найдет применение в биомедицина и биоинженерия.

Базовые модели структуры и функции белков

Программы белкового дизайна используют компьютерные модели молекулярных сил, которые заставляют белки in vivo среды. Чтобы сделать проблему разрешимой, эти силы упрощаются моделями конструкции белков. Хотя программы дизайна белков сильно различаются, они должны решать четыре основных вопроса моделирования: какова целевая структура дизайна, какая гибкость разрешена для целевой структуры, какие последовательности включаются в поиск и какое силовое поле будет использоваться для последовательности и структуры оценок.

Целевая структура

В Top7 белок был одним из первых белков, созданных для образования складок, невиданных ранее в природе.^[6]

Функция белка в значительной степени зависит от структуры белка, и рациональный дизайн белка использует эту взаимосвязь для разработки функции путем создания белков, которые имеют целевую структуру или складку. Таким образом, по определению, в рациональном дизайне белка целевая структура или ансамбль структур должны быть известны заранее. Это контрастирует с другими формами белковой инженерии, такими как направленная эволюция, где используются различные методы для поиска белков, которые выполняют определенную функцию, и с предсказание структуры белка где последовательность известна, но структура неизвестна.

Чаще всего целевая структура основана на известной структуре другого белка. Тем не менее, новые складки, невидимые в природе, становятся все более возможными. Питер С. Ким и его коллеги разработали тримеры и тетрамеры неестественных спиральных катушек, которые раньше не встречались в природе.^[4][5] Протеин Top7, разработанный в Дэвид Бейкер Лаборатория была спроектирована полностью с использованием алгоритмов дизайна белков, в совершенно новой форме.^[6] Совсем недавно Бейкер и его коллеги разработали ряд принципов для создания идеальных глобулярный белок конструкции на основе белковые складные воронки этот мост между предсказанием вторичной структуры и третичными структурами. Эти принципы, основанные как на предсказании структуры белка, так и на дизайне белка, были использованы для разработки пяти различных новых топологий белков.^[9]

Пространство последовательности

FSD-1 (показан синим цветом, PDB id: 1FSV) был первым de novo вычислительный дизайн полного белка.^[3] Целевая складка представляла собой складку цинкового пальца в остатках 33-60 структуры белка Zif268 (показаны красным, PDB id: 1ZAA). Разработанная последовательность имела очень небольшую идентичность последовательности с какой-либо известной последовательностью белка.

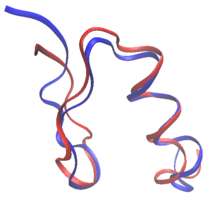
При рациональном дизайне белков белки могут быть изменены на основе последовательности и структуры известного белка или полностью с нуля в de novo белковый дизайн. При редизайне белка большинство остатков в последовательности сохраняются как их аминокислоты дикого типа, в то время как некоторым разрешается мутировать. В de novo дизайн, вся последовательность разрабатывается заново, без предварительной последовательности.

Обе de novo дизайн и переработка белков могут установить правила пространство последовательности: конкретные аминокислоты, которые разрешены в каждом положении изменяемого остатка. Например, состав поверхности Зонд RSC3 выбор антител, нейтрализующих ВИЧ, был ограничен на основании данных эволюции и баланса заряда. Многие из самых ранних попыток создания белков в значительной степени основывались на эмпирических исследованиях. правила в пространстве последовательностей.^[2] Более того, дизайн волокнистых белков обычно следует строгим правилам в отношении пространства последовательностей. Коллаген сконструированные белки, например, часто состоят из повторяющихся паттернов Gly-Pro-X.^[2] Появление вычислительных методов позволяет конструировать белки без вмешательства человека в выбор последовательности.^[3]

Структурная гибкость

Обычные программы дизайна белков используют библиотеки ротамеров для упрощения конформационного пространства боковых цепей белка. Эта анимация проходит через все ротамеры аминокислоты изолейцин на основе библиотеки Penultimate Rotamer.^[10]

В дизайне белка целевая структура (или структуры) белка известна. Однако рациональный подход к дизайну белков должен моделировать некоторые гибкость на целевой структуре, чтобы увеличить количество последовательностей, которые могут быть разработаны для этой структуры, и минимизировать вероятность сворачивания последовательности в другую структуру. Например, при редизайне белка одной небольшой аминокислоты (такой как аланин) в плотно упакованном ядре белка, очень небольшое количество мутантов может быть предсказано рациональным подходом к дизайну для сворачивания в целевую структуру, если окружающие боковые цепи не допускается переупаковка.

Таким образом, важным параметром любого процесса проектирования является степень гибкости, разрешенная как для боковых цепей, так и для магистрали. В простейших моделях остов протеина остается жестким, в то время как некоторым боковым цепям протеина позволяют изменять конформации. Однако боковые цепи могут иметь много степеней свободы в отношении длин связей, валентных углов и χ двугранные углы. Чтобы упростить это пространство, методы дизайна белков используют библиотеки ротамеров, которые принимают идеальные значения для длин связей и валентных углов, ограничивая при этом χ двугранные углы к нескольким часто наблюдаемым низкоэнергетическим конформациям, называемым ротамеры.

Библиотеки ротамеров описывают ротамеры на основе анализа многих белковых структур. Базовые библиотеки ротамеров описывают все ротамеры.^[10] Зависимые от скелета библиотеки ротамеров, напротив, описывают ротамеры как вероятность их появления в зависимости от расположения белкового скелета вокруг боковой цепи.^[11] Ротамеры, описываемые библиотеками ротамеров, обычно представляют собой области в космосе. Большинство программ дизайна белков используют одну конформацию (например, модальное значение для двугранных углов ротамера в пространстве) или несколько точек в области, описываемой ротамером; то СКОПА Программа дизайна белков, напротив, моделирует всю непрерывную область.^[12]

Хотя рациональный дизайн белка должен сохранять общую складку скелета белка, допущение некоторой гибкости скелета может значительно увеличить количество последовательностей, которые складываются в структуру, при сохранении общей складки белка.^[13] Гибкость скелета особенно важна при редизайне белка, потому что мутации в последовательности часто приводят к небольшим изменениям в структуре скелета. Более того, гибкость основной цепи может быть существенной для более сложных приложений дизайна белков, таких как предсказание связывания и дизайн ферментов. Некоторые модели гибкости основной цепи конструкции белка включают небольшие и непрерывные глобальные перемещения позвоночника, дискретные образцы позвоночника вокруг целевой складки, движения спины и гибкость петли белка.^[13][14]

Энергетическая функция

Сравнение различных функций потенциальной энергии. Самая точная энергия - это те, которые используют квантово-механические расчеты, но они слишком медленные для дизайна белков. С другой стороны, эвристические функции энергии основаны на статистических терминах и работают очень быстро. В середине находятся энергетические функции молекулярной механики, которые основаны на физике, но не так затратны с точки зрения вычислений, как квантово-механическое моделирование.^[15]

Методы рационального конструирования белков должны быть способны отличать последовательности, которые будут стабильными под целевым фолдом, от тех, которые предпочли бы другие конкурирующие состояния с низкой энергией. Таким образом, дизайн белка требует точного энергетические функции которые могут ранжировать и оценивать последовательности по тому, насколько хорошо они укладываются в целевую структуру. Однако в то же время эти энергетические функции должны учитывать расчетную вызовы за дизайном белка. Одним из самых сложных требований для успешного проектирования является функция энергии, которая является точной и простой для вычислительных расчетов.

Наиболее точные функции энергии основаны на квантовомеханическом моделировании. Однако такое моделирование происходит слишком медленно и обычно нецелесообразно для дизайна белков. Вместо этого многие алгоритмы проектирования белков используют либо физические функции энергии, адаптированные из молекулярная механика программы моделирования, энергетические функции, основанные на знаниях или их гибридное сочетание. Имеется тенденция к использованию функций потенциальной энергии, основанных на физике.^[15]

Физические функции энергии, такие как ЯНТАРЬ и Очарование, обычно получаются из квантово-механического моделирования и экспериментальных данных из термодинамики, кристаллографии и спектроскопии.^[16] Эти энергетические функции обычно упрощают функцию физической энергии и делают их попарно разложимыми, что означает, что общая энергия конформации белка может быть вычислена путем добавления попарной энергии между каждой парой атомов, что делает их привлекательными для алгоритмов оптимизации. Физические функции энергии обычно моделируют притягивающе-отталкивающий Леннард-Джонс член между атомами и попарно электростатика кулоновский термин^[17] между несвязанными атомами.

Водородные связи, опосредованные водой, играют ключевую роль в связывании белок-белок. Одно из таких взаимодействий показано между остатками D457, S365 в тяжелой цепи ВИЧ-нейтрализующего широкого антитела VRC01 (зеленый) и остатками N58 и Y59 в белке оболочки ВИЧ GP120 (фиолетовый).^[18]

Статистические потенциалы, в отличие от потенциалов, основанных на физике, обладают тем преимуществом, что их можно быстро вычислить, неявно учитывать сложные эффекты и они менее чувствительны к небольшим изменениям в структуре белка.^[19] Эти энергетические функции на основе получения значений энергии от частоты появления в структурной базе данных.

Однако дизайн белков предъявляет требования, которые иногда могут быть ограничены в силовых полях молекулярной механики. Силовые поля молекулярной механики, которые использовались в основном в молекулярно-динамическом моделировании, оптимизированы для моделирования отдельных последовательностей, но конструкция белка ищет множество конформаций многих последовательностей. Таким образом, силовые поля молекулярной механики должны быть адаптированы для дизайна белков. На практике энергетические функции дизайна белков часто включают как статистические, так и физические термины. Например, функция энергии Розетты, одна из наиболее часто используемых функций энергии, включает термины энергии, основанные на физике, происходящие из функции энергии CHARMM, и статистические термины энергии, такие как вероятность ротамера и электростатика, основанная на знаниях. Как правило, энергетические функции сильно настраиваются между лабораториями и специально подбираются для каждого проекта.^[16]

Проблемы эффективного проектирования энергетических функций

Вода составляет большинство молекул, окружающих белки, и является основным двигателем структуры белка. Таким образом, моделирование взаимодействия между водой и белком жизненно важно при разработке белков. Количество молекул воды, которые взаимодействуют с белком в любой момент времени, огромно, и каждая из них имеет большое количество степеней свободы и партнеров по взаимодействию. Вместо этого программы дизайна белков моделируют большинство таких молекул воды как континуум, моделируя как гидрофобный эффект, так и поляризацию сольватации.^[16]

Отдельные молекулы воды иногда могут играть решающую структурную роль в ядре белков и во взаимодействиях белок-белок или белок-лиганд. Неспособность смоделировать такие воды может привести к неправильному предсказанию оптимальной последовательности межбелкового интерфейса. В качестве альтернативы к ротамерам можно добавлять молекулы воды.

^[16]

Как проблема оптимизации

Эта анимация иллюстрирует сложность поиска дизайна белка, при котором обычно сравниваются все конформации ротамера из всех возможных мутаций по всем остаткам. В этом примере остаткам Phe36 и His 106 позволяют мутировать, соответственно, в аминокислоты Tyr и Asn. Phe и Tyr имеют по 4 ротамера в библиотеке ротамеров, в то время как Asn и His имеют 7 и 8 ротамеров, соответственно, в библиотеке ротамеров (из библиотеки предпоследних ротамеров Ричардсона.^[10]). Анимация проходит через все (4 + 4) x (7 + 8) = 120 вариантов. Показанная структура соответствует миоглобину, PDB id: 1mbn.

Цель дизайна белка - найти последовательность белка, которая сворачивается в целевую структуру. Таким образом, алгоритм дизайна белка должен искать все конформации каждой последовательности относительно целевой складки и ранжировать последовательности в соответствии с конформацией с наименьшей энергией каждой из них, как определено функцией энергии дизайна белка. Таким образом, типичными входными данными для алгоритма конструирования белка являются целевая складка, пространство последовательностей, структурная гибкость и функция энергии, в то время как выходными данными являются одна или несколько последовательностей, которые, как прогнозируется, будут стабильно складываться в целевую структуру.

Однако количество кандидатных белковых последовательностей растет экспоненциально с увеличением количества белковых остатков; например, есть 20¹⁰⁰ последовательности белка длиной 100. Кроме того, даже если конформации боковой цепи аминокислот ограничены несколькими ротамерами (см. Структурная гибкость ), это приводит к экспоненциальному количеству конформаций для каждой последовательности. Таким образом, в нашем белке из 100 остатков и при условии, что каждая аминокислота имеет ровно 10 ротамеров, алгоритм поиска, который ищет это пространство, должен будет искать более 200¹⁰⁰ конформации белков.

Наиболее распространенные энергетические функции могут быть разложены на попарные члены между ротамерами и типами аминокислот, что делает проблему комбинаторной, и для ее решения можно использовать мощные алгоритмы оптимизации. В этих случаях полная энергия каждой конформации, принадлежащей каждой последовательности, может быть сформулирована как сумма индивидуальных и попарных членов между положениями остатков. Если разработчика интересует только лучшая последовательность, алгоритм дизайна белка требует только конформации с наименьшей энергией последовательности с наименьшей энергией. В этих случаях идентичность аминокислот каждого ротамера можно игнорировать, и все ротамеры, принадлежащие к разным аминокислотам, можно рассматривать одинаково. Позволять р_я быть ротамером в положении остатка я в белковой цепи, и E (р_я) потенциальная энергия между внутренними атомами ротамера. Позволять E(р_я, р_j) - потенциальная энергия между р_я и ротамер р_j в положении остатка j. Затем мы определяем задачу оптимизации как задачу нахождения соответствия минимальной энергии (E_Т):

${\displaystyle \min E_{T}=\sum _{i}{\Big [}E_{i}(r_{i})+\sum _{i\neq j}E_{ij}(r_{i},r_{j}){\Big ]}\,}$

(1)

Проблема минимизации E_Т является NP-жесткий проблема.^[14][20][21] Несмотря на то, что класс проблем является NP-сложным, на практике многие примеры дизайна белков могут быть решены точно или удовлетворительно оптимизированы с помощью эвристических методов.

Алгоритмы

Несколько алгоритмов были разработаны специально для задачи дизайна белков. Эти алгоритмы можно разделить на два широких класса: точные алгоритмы, такие как тупиковое устранение, это отсутствие время выполнения гарантирует, но гарантирует качество решения; и эвристический алгоритмы, такие как Монте-Карло, которые быстрее точных алгоритмов, но не дают гарантий оптимальности результатов. Точные алгоритмы гарантируют, что в процессе оптимизации были получены оптимальные результаты в соответствии с конструктивной моделью белка. Таким образом, если прогнозы точных алгоритмов терпят неудачу, когда они экспериментально подтверждены, то источник ошибки может быть отнесен к функции энергии, допустимой гибкости, пространству последовательностей или целевой структуре (например, если она не может быть разработана для)^[22]

Некоторые алгоритмы дизайна белков перечислены ниже. Хотя эти алгоритмы решают только самую базовую формулировку проблемы дизайна белка, уравнение (1), когда цель оптимизации изменяется из-за того, что разработчики вводят улучшения и расширения в модель дизайна белка, такие как улучшения допустимой структурной гибкости (например, гибкости основной цепи белка) или включение сложных энергетических терминов, многие из расширений дизайна белка, которые улучшают моделирование построены на этих алгоритмах. Например, Rosetta Design включает в себя сложные энергетические термины и гибкость магистрали с использованием Монте-Карло в качестве основного алгоритма оптимизации. Алгоритмы OSPREY основаны на алгоритме устранения тупика и A *, чтобы включать непрерывные движения основной и боковой цепи. Таким образом, эти алгоритмы дают хорошее представление о различных типах алгоритмов, доступных для дизайна белков.

В июле 2020 года ученые сообщили о разработке процесса на основе ИИ с использованием базы данных генома за основанный на эволюции разработка новых белков. Они использовали глубокое обучение для определения правил проектирования.^[23][24]

С математическими гарантиями

Тупиковое устранение

Основная статья: Тупиковое устранение

Алгоритм устранения тупика (DEE) итеративно сокращает пространство поиска проблемы, удаляя ротамеры, которые, как можно доказать, не являются частью глобальной конформации с наименьшей энергией (GMEC). На каждой итерации алгоритм исключения тупика сравнивает все возможные пары ротамеров в каждой позиции остатка и удаляет каждый ротамер. р'_я который, как можно показать, всегда имеет более высокую энергию, чем другой ротамер р_я и поэтому не является частью GMEC:

${\displaystyle E(r_{i}^{\prime })+\sum _{j\neq i}\min _{r_{j}}E(r_{i}^{\prime },r_{j})>E(r_{i})+\sum _{j\neq i}\max _{r_{j}}E(r_{i},r_{j})}$

Другие мощные расширения алгоритма устранения тупиков включают: критерий исключения пар, а обобщенный критерий исключения тупика. Этот алгоритм также был расширен для работы с ротамерами непрерывного действия с доказываемыми гарантиями.

Хотя алгоритм исключения тупика выполняется за полиномиальное время на каждой итерации, он не может гарантировать сходимость. Если после определенного количества итераций алгоритм исключения тупика больше не сокращает ротамеры, то необходимо либо объединить ротамеры, либо использовать другой алгоритм поиска для поиска оставшегося пространства поиска. В таких случаях устранение тупика действует как алгоритм предварительной фильтрации для уменьшения пространства поиска, в то время как другие алгоритмы, такие как A *, Монте-Карло, линейное программирование или FASTER, используются для поиска оставшегося пространства поиска.^[14]

Ветвь и переплет

Основная статья: Ветвь и переплет

Конформационное пространство конструкции белка можно представить как дерево, где белковые остатки упорядочены произвольным образом, а дерево разветвляется на каждом из ротамеров в остатке. Ветвь и переплет алгоритмы используют это представление для эффективного изучения дерева соответствия: на каждом разветвление, алгоритмы ветвей и границ граница конформационное пространство и исследуем только перспективные отрасли.^[14][25][26]

Популярный алгоритм поиска дизайна белков - это Алгоритм поиска A *.^[14][26] A * вычисляет нижнюю границу оценки для каждого частичного пути дерева, которая ограничивает (с гарантиями) нижнюю границу энергии каждого из расширенных ротамеров. Каждое частичное подтверждение добавляется в очередь приоритетов, и на каждой итерации частичный путь с самой низкой нижней границей извлекается из очереди и расширяется. Алгоритм останавливается после того, как будет перечислено полное соответствие, и гарантирует, что соответствие является оптимальным.

Оценка A * ж в белковой конструкции состоит из двух частей, f = g + h. грамм - это точная энергия ротамеров, которые уже были присвоены частичной конформации. час - нижняя граница энергии ротамеров, которая еще не была задана. Каждый разработан следующим образом, где d - это индекс последнего присвоенного остатка в частичной конформации.

${\displaystyle g=\sum _{i=1}^{d}(E(r_{i})+\sum _{j=i+1}^{d}E(r_{i},r_{j}))}$

${\displaystyle h=\sum _{j=d+1}^{n}[\min _{r_{j}}(E(r_{j})+\sum _{i=1}^{d}E(r_{i},r_{j})+\sum _{k=j+1}^{n}\min _{r_{k}}E(r_{j},r_{k}))]}$

Целочисленное линейное программирование

Дальнейшая информация: Линейное программирование § Целочисленные неизвестные, и Целочисленное программирование

Проблема оптимизации E_Т (Уравнение (1)) легко сформулировать как целочисленная линейная программа (ILP).^[27] Одна из наиболее эффективных формулировок использует бинарные переменные для представления присутствия ротамера и ребер в конечном растворе и ограничивает раствор, чтобы он имел ровно один ротамер для каждого остатка и одно попарное взаимодействие для каждой пары остатков:

${\displaystyle \ \min \sum _{i}\sum _{r_{i}}E_{i}(r_{i})q_{i}(r_{i})+\sum _{j\neq i}\sum _{r_{j}}E_{ij}(r_{i},r_{j})q_{ij}(r_{i},r_{j})\,}$

s.t.

${\displaystyle \sum _{r_{i}}q_{i}(r_{i})=1,\ \forall i}$

${\displaystyle \sum _{r_{j}}q_{ij}(r_{i},r_{j})=q_{i}(r_{i}),\forall i,r_{i},j}$

${\displaystyle q_{i},q_{ij}\in \{0,1\}}$

Решатели ILP, такие как CPLEX, может вычислить точное оптимальное решение для больших примеров проблем проектирования белков. Эти решатели используют релаксация линейного программирования проблемы, где q_я и q_ij могут принимать непрерывные значения в сочетании с разделить и разрезать алгоритм для поиска оптимального решения только в небольшой части конформационного пространства. Было показано, что решатели ILP решают многие примеры проблемы размещения боковой цепи.^[27]

Основанные на передаче сообщений приближения к двойственному линейному программированию

Решатели ILP зависят от алгоритмов линейного программирования (LP), таких как Симплекс или же барьер основанные на методах выполнения релаксации ЛП на каждой ветви. Эти алгоритмы LP были разработаны как методы оптимизации общего назначения и не оптимизированы для решения задачи проектирования белков (уравнение (1)). Как следствие, релаксация LP становится узким местом для решателей ILP, когда размер проблемы велик.^[28] В последнее время появилось несколько альтернатив, основанных на алгоритмы передачи сообщений были разработаны специально для оптимизации LP-релаксации проблемы дизайна белка. Эти алгоритмы могут аппроксимировать как двойной или первобытный примеры целочисленного программирования, но для обеспечения гарантий оптимальности они наиболее полезны, когда используются для аппроксимации двойственной задачи проектирования белков, поскольку аппроксимация двойной гарантирует, что никакие решения не будут упущены. Приближения на основе передачи сообщений включают передача сообщений о максимальном продукте алгоритм,^[29][30] и передача сообщений линейное программирование алгоритм.^[31]

Алгоритмы оптимизации без гарантий

Монте-Карло и имитация отжига

Монте-Карло - один из наиболее широко используемых алгоритмов для дизайна белков.В своей простейшей форме алгоритм Монте-Карло выбирает остаток случайным образом, и в этом остатке оценивается случайно выбранный ротамер (любой аминокислоты).^[21] Новая энергия белка, E_новый сравнивается со старой энергией E_Старый а новый ротамер принято с вероятностью:

${\displaystyle p=e^{-\beta (E_{\text{new}}-E_{\text{old}}))},}$

куда β это Постоянная Больцмана и температура Т можно выбрать так, чтобы в начальных раундах он был высоким и медленно отожженный преодолевать локальные минимумы.^[12]

БЫСТРЕЕ

Алгоритм FASTER использует комбинацию детерминированных и стохастических критериев для оптимизации аминокислотных последовательностей. FASTER сначала использует DEE для устранения ротамеров, которые не являются частью оптимального решения. Затем серия итерационных шагов оптимизирует назначение ротамера.^[32][33]

Распространение веры

В распространение веры для дизайна белков алгоритм обменивается сообщениями, описывающими вера что каждый остаток имеет примерно вероятность присутствия каждого ротамера в соседних остатках. Алгоритм обновляет сообщения на каждой итерации и выполняет итерацию до сходимости или до фиксированного количества итераций. Конвергенция не гарантируется в дизайне белков. Сообщение м_{я → j}(р_j что остаток я отправляет каждому ротамеру (р_j в соседнем остатке j определяется как:

${\displaystyle m_{i\to j}(r_{j})=\max _{r_{i}}{\Big (}e^{\frac {-E_{i}(r_{i})-E_{ij}(r_{i},r_{j})}{T}}{\Big )}\prod _{k\in N(i)\backslash j}m_{k\to i(r_{i})}}$

Распространение убеждений как о максимальном продукте, так и о сумме-произведении использовалось для оптимизации дизайна белков.

Приложения и примеры разработанных белков

Ферментный дизайн

Дизайн нового ферменты это использование дизайна белков с огромными приложениями в биоинженерии и биомедицине. В общем, разработка структуры белка может отличаться от разработки фермента, потому что дизайн ферментов должен учитывать множество состояний, участвующих в каталитический механизм. Однако белковый дизайн является необходимым условием de novo дизайн ферментов, потому что, по крайней мере, конструкция катализаторов требует каркаса, в который может быть встроен каталитический механизм.^[34]

Большой прогресс в de novo Дизайн и модернизация ферментов были сделаны в первом десятилетии 21 века. В трех крупных исследованиях Дэвид Бейкер с коллегами de novo разработанные ферменты для ретро-альдольная реакция,^[35] реакция Кемпа-элиминирования,^[36] и для Реакция Дильса-Альдера.^[37] Более того, Стивен Мэйо и его коллеги разработали итерационный метод создания наиболее эффективного известного фермента для реакции удаления Кемпа.^[38] Также в лаборатории Брюс Дональд, вычислительный дизайн белка использовался для переключения специфичности одного из белковые домены из нерибосомальная пептидная синтетаза что производит Грамицидин S, из натурального субстрата фенилаланин к другим непознанным субстратам, включая заряженные аминокислоты; модифицированные ферменты имели активность, близкую к активности дикого типа.^[39]

Дизайн для близости

Белковые взаимодействия участвуют в большинстве биотических процессов. Многие из тяжело поддающихся лечению заболеваний, такие как Альцгеймера много форм рак (например., TP53 ) и вируса иммунодефицита человека (ВИЧ ) инфекция вовлекает белок-белковые взаимодействия. Таким образом, для лечения таких заболеваний желательно разработать белковые или белковоподобные терапевтические средства, которые связывают одного из партнеров взаимодействия и, таким образом, нарушают вызывающее заболевание взаимодействие. Это требует разработки белковых терапевтических средств для близость к своему партнеру.

Взаимодействия белок-белок могут быть разработаны с использованием алгоритмов дизайна белков, поскольку принципы, определяющие стабильность белка, также определяют связывание белок-белок. Дизайн белок-белкового взаимодействия, однако, представляет проблемы, обычно не встречающиеся при дизайне белков. Одна из наиболее важных проблем состоит в том, что, как правило, интерфейсы между белками более полярны, чем ядра белков, и связывание включает компромисс между десольватацией и образованием водородных связей.^[40] Чтобы преодолеть эту проблему, Брюс Тидор и его коллеги разработали метод повышения аффинности антител, сосредоточив внимание на электростатическом воздействии. Они обнаружили, что для антител, разработанных в исследовании, снижение затрат на десольватацию остатков на границе раздела увеличивало аффинность связывающей пары.^[40][41][42]

Оценка привязки прогнозов

Энергетические функции дизайна белков должны быть адаптированы для оценки предсказаний связывания, поскольку связывание предполагает компромисс между наименьшими и низкими значениями.энергия конформации свободных белков (E_п и E_L) и наиболее низкоэнергетической конформации связанного комплекса (E_PL):

${\displaystyle \Delta _{G}=E_{PL}-E_{P}-E_{L}}$.

Алгоритм K * аппроксимирует константу связывания алгоритма, включая конформационную энтропию в расчет свободной энергии. Алгоритм K * рассматривает только низкоэнергетические конформации свободных и связанных комплексов (обозначаемых множествами п, L, и PL) для аппроксимации статистических сумм каждого комплекса:^[14]

${\displaystyle K^{*}={\frac {\sum \limits _{x\in PL}e^{-E(x)/RT}}{\sum \limits _{x\in P}e^{-E(x)/RT}\sum \limits _{x\in L}e^{-E(x)/RT}}}}$

Дизайн для специфики

Дизайн белок-белковых взаимодействий должен быть высокоспецифичным, потому что белки могут взаимодействовать с большим количеством белков; успешный дизайн требует отборных связующих. Таким образом, алгоритмы дизайна белков должны уметь различать целевые (или позитивный дизайн) и нецелевое связывание (или отрицательный дизайн).^[2][40] Один из самых ярких примеров дизайна для специфики - это дизайн конкретных bZIP -связывающие пептиды от Amy Keating и соавторов для 19 из 20 семейств bZIP; 8 из этих пептидов были специфичны для предполагаемого партнера по сравнению с конкурирующими пептидами.^[40][43][44] Кроме того, Андерсон и его коллеги также использовали положительный и отрицательный дизайн для прогнозирования мутаций в активном сайте мишени лекарственного средства, которые придали устойчивость к новому лекарству; положительный дизайн использовали для поддержания активности дикого типа, тогда как отрицательный дизайн использовали для нарушения связывания лекарственного средства.^[45] Недавняя вычислительная модернизация, проведенная Костасом Маранасом с коллегами, также позволила экспериментально переключить кофактор специфика Candida boidinii ксилозоредуктаза из НАДФН к НАДН.^[46]

Белковая шлифовка

Замена поверхности протеином заключается в формировании поверхности протеина с сохранением целостности складок, сердцевины и граничных областей протеина. Белковая шлифовка особенно полезна для изменения связывания белка с другими белками. Одним из наиболее важных применений обновления протеина было создание зонда RSC3 для отбора широко нейтрализующих антител к ВИЧ в Исследовательском центре вакцин NIH. Во-первых, для конструирования были отобраны остатки за пределами границы связывания между белком оболочки ВИЧ gp120 и ранее обнаруженным b12-антителом. Затем последовательность с разнесением была выбрана на основании информации об эволюции, растворимости, сходства с диким типом и других соображений. Затем программное обеспечение RosettaDesign было использовано для поиска оптимальных последовательностей в выбранном пространстве последовательностей. Позднее RSC3 был использован для обнаружения широко нейтрализующего антитела VRC01 в сыворотке длительно инфицированного ВИЧ индивидуума, не прогрессирующего.^[47]

Дизайн глобулярных белков

Глобулярные белки белки, которые содержат гидрофобное ядро ​​и гидрофильную поверхность. Глобулярные белки часто имеют стабильную структуру, в отличие от волокнистые белки, которые имеют множественные конформации. Трехмерную структуру глобулярных белков обычно легче определить с помощью Рентгеновская кристаллография и ядерный магнитный резонанс чем как волокнистые белки, так и мембранные белки, что делает глобулярные белки более привлекательными для дизайна белков, чем другие типы белков. Наиболее успешные конструкции белков включали глобулярные белки. Обе RSD-1, и Top7 мы de novo конструкции глобулярных белков. Еще пять белковых структур были разработаны, синтезированы и проверены в 2012 году группой Бейкера. Эти новые белки не выполняют никаких биотических функций, но структуры предназначены для того, чтобы действовать как строительные блоки, которые могут быть расширены для включения функциональных активных центров. Структуры были найдены вычислительным путем с использованием новой эвристики, основанной на анализе соединительных циклов между частями последовательности, которые определяют вторичные структуры.^[48]

Дизайн мембранных белков

Были успешно созданы несколько трансмембранных белков,^[49] наряду со многими другими мембраносвязанными пептидами и белками.^[50] Недавно Костас Маранас и его коллеги разработали автоматизированный инструмент.^[51] изменить размер пор внешней мембраны Porin Type-F (OmpF) с Кишечная палочка до любого желаемого размера субнм и собрали их в мембраны для выполнения точного разделения по шкале Ангстрема.

Другие приложения

Одно из наиболее желательных применений дизайна белков - это биосенсоры, белки, которые будут определять присутствие определенных соединений. Некоторые попытки создания биосенсоров включают датчики неестественных молекул, в том числе TNT.^[52] Совсем недавно Кульман и его коллеги разработали биосенсор PAK1.^[53]

Смотрите также

• Программное обеспечение для молекулярного дизайна
• Белковая инженерия
• Программное обеспечение для предсказания структуры белка
• Сравнение программного обеспечения для моделирования молекулярной механики

Рекомендации

1. Корендович, Иван (19 марта 2018 г.). «Минималистичный дизайн пептидных и белковых катализаторов». Американское химическое общество. Получено 22 марта, 2018.
2. Ричардсон, Дж. С.; Ричардсон, округ Колумбия (июль 1989 г.). «Дизайн de novo белковых структур». Тенденции в биохимических науках. 14 (7): 304–9. Дои:10.1016/0968-0004(89)90070-4. PMID  2672455.
3. Дахият, Б.И.; Мэйо, SL (3 октября 1997 г.). «Дизайн белка De novo: полностью автоматизированный выбор последовательности». Наука. 278 (5335): 82–7. CiteSeerX  10.1.1.72.7304. Дои:10.1126 / science.278.5335.82. PMID  9311930.
4. Гордон, ДБ; Marshall, SA; Мэйо, SL (август 1999 г.). «Энергетические функции для дизайна белков». Текущее мнение в структурной биологии. 9 (4): 509–13. Дои:10.1016 / s0959-440x (99) 80072-4. PMID  10449371.
5. Харбери, ПБ; Plecs, JJ; Тидор, Б; Альбер, Т; Ким, PS (20 ноября 1998 г.). «Белковая конструкция с высоким разрешением и свободой позвоночника». Наука. 282 (5393): 1462–7. Дои:10.1126 / science.282.5393.1462. PMID  9822371.
6. Kuhlman, B; Дантас, G; Ireton, GC; Варани, G; Стоддард, Б.Л .; Бейкер, Д. (21 ноября 2003 г.). «Дизайн новой глобулярной белковой складки с точностью до атомного уровня». Наука. 302 (5649): 1364–8. Bibcode:2003Наука ... 302.1364K. Дои:10.1126 / science.1089427. PMID  14631033. S2CID  1939390.
7. Sterner, R; Merkl, R; Раушель, FM (май 2008 г.). «Вычислительный дизайн ферментов». Химия и биология. 15 (5): 421–3. Дои:10.1016 / j.chembiol.2008.04.007. PMID  18482694.
8. Ву, Х; Ян, З.Ы .; Ли, У; Hogerkorp, CM; Schief, WR; Моряк, МС; Чжоу, Т; Шмидт, С.Д .; Wu, L; Сюй, L; Лонго, Н.С. McKee, K; О'Делл, S; Громче, МК; Wycuff, DL; Feng, Y; Nason, M; Дориа-Роуз, N; Коннорс, М; Квонг, PD; Рёдерер, М; Wyatt, RT; Набель, ГДж; Маскола-младший (13 августа 2010 г.). «Рациональный дизайн конверта позволяет идентифицировать широко нейтрализующие человеческие моноклональные антитела к ВИЧ-1». Наука. 329 (5993): 856–61. Bibcode:2010Sci ... 329..856W. Дои:10.1126 / science.1187659. ЧВК  2965066. PMID  20616233.
9. Höcker, B (8 ноября 2012 г.). «Структурная биология: набор инструментов для дизайна белков». Природа. 491 (7423): 204–5. Bibcode:2012Натура.491..204H. Дои:10.1038 / 491204a. PMID  23135466. S2CID  4426247.
10. Ловелл, Южная Каролина; Word, JM; Ричардсон, Дж. С.; Ричардсон, округ Колумбия (15 августа 2000 г.). «Предпоследняя библиотека ротамеров». Белки. 40 (3): 389–408. CiteSeerX  10.1.1.555.4071. Дои:10.1002 / 1097-0134 (20000815) 40: 3 <389 :: AID-PROT50> 3.0.CO; 2-2. PMID  10861930.
11. Шаповалов М.В.; Данбрак Р.Л., младший (8 июня 2011 г.). «Сглаженная библиотека ротамеров, зависимая от остова, для белков, полученных на основе оценок и регрессий адаптивной плотности ядра». Структура. 19 (6): 844–58. Дои:10.1016 / j.str.2011.03.019. ЧВК  3118414. PMID  21645855.
12. Самиш, я; MacDermaid, CM; Перес-Агилар, JM; Савен, JG (2011). «Теоретический и вычислительный дизайн белков». Ежегодный обзор физической химии. 62: 129–49. Bibcode:2011ARPC ... 62..129S. Дои:10.1146 / annurev-physchem-032210-103509. PMID  21128762.
13. Манделл, диджей; Кортемме, Т (Август 2009 г.). «Гибкость основы в вычислительном дизайне белков» (PDF). Текущее мнение в области биотехнологии. 20 (4): 420–8. Дои:10.1016 / j.copbio.2009.07.006. PMID  19709874.
14. Дональд, Брюс Р. (2011). Алгоритмы структурной молекулярной биологии. Кембридж, Массачусетс: MIT Press.
15. Боас, Ф. Э. и Харбери, П. Б. (2007). «Возможные энергетические функции для дизайна белков». Текущее мнение в структурной биологии. 17 (2): 199–204. Дои:10.1016 / j.sbi.2007.03.006. PMID  17387014.
16. Боас, ИП; Харбери, ПБ (апрель 2007 г.). «Возможные энергетические функции для дизайна белков». Текущее мнение в структурной биологии. 17 (2): 199–204. Дои:10.1016 / j.sbi.2007.03.006. PMID  17387014.
17. Вискарра, CL; Мэйо, SL (декабрь 2005 г.). «Электростатика в вычислительном дизайне белков». Современное мнение в области химической биологии. 9 (6): 622–6. Дои:10.1016 / j.cbpa.2005.10.014. PMID  16257567.
18. Чжоу, Т; Георгиев, I; Ву, Х; Ян, З.Ы .; Дай, К; Finzi, A; Kwon, YD; Scheid, JF; Ши, Вт; Сюй, L; Ян, Y; Чжу, Дж; Нуссенцвейг, MC; Содроски, Дж; Шапиро, Л; Набель, ГДж; Маскола, младший; Квонг, PD (13 августа 2010 г.). «Структурная основа для широкой и мощной нейтрализации ВИЧ-1 антителом VRC01». Наука. 329 (5993): 811–7. Bibcode:2010Sci ... 329..811Z. Дои:10.1126 / science.1192819. ЧВК  2981354. PMID  20616231.
19. Мендес, Дж; Guerois, R; Серрано, Л. (август 2002 г.). «Энергетическая оценка в белковом дизайне». Текущее мнение в структурной биологии. 12 (4): 441–6. Дои:10.1016 / s0959-440x (02) 00345-7. PMID  12163065.
20. Pierce, NA; Winfree, E (октябрь 2002 г.). «Белковый дизайн NP-жесткий». Белковая инженерия. 15 (10): 779–82. Дои:10.1093 / белок / 15.10.779. PMID  12468711.
21. Фойгт, Калифорния; Гордон, ДБ; Мэйо, SL (9 июня 2000 г.). «Торговая точность для скорости: количественное сравнение алгоритмов поиска в дизайне белковой последовательности». Журнал молекулярной биологии. 299 (3): 789–803. CiteSeerX  10.1.1.138.2023. Дои:10.1006 / jmbi.2000.3758. PMID  10835284.
22. Hong, EJ; Lippow, SM; Тидор, Б; Лозано-Перес, Т. (сентябрь 2009 г.). «Оптимизация ротамеров для дизайна белков посредством оценки MAP и уменьшения размера проблемы». Журнал вычислительной химии. 30 (12): 1923–45. Дои:10.1002 / jcc.21188. ЧВК  3495010. PMID  19123203.
23. «Машинное обучение раскрывает рецепт создания искусственных белков». Phys.org. Получено 17 августа, 2020.
24. Расс, Уильям П .; Фиглюцци, Маттео; Стокер, Кристиан; Барра-Шарле, Пьер; Соколич, Михаил; Каст, Питер; Хилверт, Дональд; Монассон, Реми; Кокко, Симона; Weigt, Мартин; Ранганатан, Рама (2020). «Основанная на эволюции модель для разработки ферментов хоризматемутазы». Наука. 369 (6502): 440. Bibcode:2020Sci ... 369..440R. Дои:10.1126 / science.aba3304 (неактивно 30 ноября 2020 г.).
25. Гордон, ДБ; Мэйо, SL (15 сентября 1999 г.). «Branch-and-terminate: комбинаторный алгоритм оптимизации для дизайна белка». Структура. 7 (9): 1089–98. Дои:10.1016 / s0969-2126 (99) 80176-2. PMID  10508778.
26. Leach, AR; Лимон, AP (1 ноября 1998 г.). «Изучение конформационного пространства белковых боковых цепей с использованием тупикового исключения и алгоритма A *». Белки. 33 (2): 227–39. CiteSeerX  10.1.1.133.7986. Дои:10.1002 / (sici) 1097-0134 (19981101) 33: 2 <227 :: aid-prot7> 3.0.co; 2-f. PMID  9779790.
27. Кингсфорд, CL; Chazelle, B; Сингх, М. (1 апреля 2005 г.). «Решение и анализ задач позиционирования сайдчейна с использованием линейного и целочисленного программирования». Биоинформатика. 21 (7): 1028–36. Дои:10.1093 / биоинформатика / bti144. PMID  15546935.
28. Яновер, Чен; Талья Мельцер; Яир Вайс (2006). «Расслабление линейного программирования и распространение убеждений - эмпирическое исследование». Журнал исследований в области машинного обучения. 7: 1887–1907.
29. Уэйнрайт, Мартин Дж; Томми С. Яаккола; Алан С. Вилски (2005). «Оценка MAP через соглашение о деревьях: передача сообщений и линейное программирование». IEEE Transactions по теории информации. 51 (11): 3697–3717. CiteSeerX  10.1.1.71.9565. Дои:10.1109 / tit.2005.856938. S2CID  10007532.
30. Колмогоров, Владимир (28 октября 2006 г.). «Конвергентная передача сообщений с перевесом дерева для минимизации энергии». IEEE Transactions по анализу шаблонов и машинному анализу. 28 (10): 1568–1583. Дои:10.1109 / TPAMI.2006.200. PMID  16986540. S2CID  8616813.
31. Глоберсон, Амир; Томми С. Яаккола (2007). «Исправление max-product: конвергентные алгоритмы передачи сообщений для MAP LP-релаксации». Достижения в системах обработки нейронной информации.
32. Allen, BD; Мэйо, SL (30 июля 2006 г.). «Значительное повышение производительности алгоритма оптимизации БЫСТРЕЕ». Журнал вычислительной химии. 27 (10): 1071–5. CiteSeerX  10.1.1.425.5418. Дои:10.1002 / jcc.20420. PMID  16685715. S2CID  769053.
33. Десмет, Дж; Spriet, J; Ластерс, I (1 июля 2002 г.). «Быстрая и точная топология боковой цепи и оптимизация энергии (FASTER) как новый метод оптимизации структуры белка». Белки. 48 (1): 31–43. Дои:10.1002 / prot.10131. PMID  12012335. S2CID  21524437.
34. Бейкер, Д. (октябрь 2010 г.). «Захватывающий, но непростой путь к разработке вычислительных ферментов». Белковая наука. 19 (10): 1817–9. Дои:10.1002 / pro.481. ЧВК  2998717. PMID  20717908.
35. Цзян, Линь; Альтхофф, Эрик А .; Clemente, Fernando R .; Дойл, Линдси; Ротлисбергер, Даниэла; Зангеллини, Александр; Gallaher, Jasmine L .; Беткер, Джейми Л .; Танака, Фуджи (2008). «Вычислительный дизайн ретро-альдольных ферментов De Novo». Наука. 319 (5868): 1387–91. Bibcode:2008Sci ... 319.1387J. Дои:10.1126 / science.1152692. ЧВК  3431203. PMID  18323453.
36. Рётлисбергер, Даниэла; Херсонский, Ольга; Wollacott, Andrew M .; Цзян, Линь; Дечанси, Джейсон; Беткер, Джейми; Gallaher, Jasmine L .; Альтхофф, Эрик А .; Зангеллини, Александр (2008). «Катализаторы удаления Кемпа с помощью вычислительного фермента». Природа. 453 (7192): 190–5. Bibcode:2008Натура.453..190р. Дои:10.1038 / природа06879. PMID  18354394.
37. Siegel, JB; Зангеллини, А; Ловик, HM; Поцелуй, G; Ламберт, АР; Сент-Клер, JL; Gallaher, JL; Hilvert, D; Гелб, MH; Стоддард, Б.Л .; Houk, KN; Майкл, ИП; Бейкер, Д. (16 июля 2010 г.). «Вычислительный дизайн ферментного катализатора стереоселективной бимолекулярной реакции Дильса-Альдера». Наука. 329 (5989): 309–13. Bibcode:2010Sci ... 329..309S. Дои:10.1126 / science.1190239. ЧВК  3241958. PMID  20647463.
38. Privett, HK; Поцелуй, G; Ли, ТМ; Бломберг, Р.; Чика, РА; Thomas, LM; Hilvert, D; Houk, KN; Мэйо, SL (6 марта 2012 г.). «Итерационный подход к вычислительному дизайну ферментов». Труды Национальной академии наук Соединенных Штатов Америки. 109 (10): 3790–5. Bibcode:2012ПНАС..109.3790П. Дои:10.1073 / pnas.1118082108. ЧВК  3309769. PMID  22357762.
39. Chen, CY; Георгиев, I; Андерсон, AC; Дональд, Б.Р. (10 марта 2009 г.). «Перепроектирование активности ферментов на основе вычислительной структуры». Труды Национальной академии наук Соединенных Штатов Америки. 106 (10): 3764–9. Bibcode:2009PNAS..106.3764C. Дои:10.1073 / pnas.0900266106. ЧВК  2645347. PMID  19228942.
40. Karanicolas, J; Кульман, Б. (август 2009 г.). «Вычислительный дизайн аффинности и специфичности на межбелковых интерфейсах». Текущее мнение в структурной биологии. 19 (4): 458–63. Дои:10.1016 / j.sbi.2009.07.005. ЧВК  2882636. PMID  19646858.
41. Шойхет, Б.К. (октябрь 2007 г.). «Нет бесплатного энергетического обеда». Природа Биотехнологии. 25 (10): 1109–10. Дои:10.1038 / nbt1007-1109. PMID  17921992. S2CID  5527226.
42. Lippow, SM; Wittrup, KD; Тидор, Б. (октябрь 2007 г.). «Вычислительный дизайн улучшения аффинности антител после созревания in vivo». Природа Биотехнологии. 25 (10): 1171–6. Дои:10.1038 / nbt1336. ЧВК  2803018. PMID  17891135.
43. Schreiber, G; Китинг, AE (февраль 2011 г.). «Специфичность связывания с белками по сравнению с беспорядочными половыми связями». Текущее мнение в структурной биологии. 21 (1): 50–61. Дои:10.1016 / j.sbi.2010.10.002. ЧВК  3053118. PMID  21071205.
44. Григорян, Г; Рейнке, AW; Китинг, AE (16 апреля 2009 г.). «Дизайн специфичности взаимодействия с белками дает селективные bZIP-связывающие пептиды». Природа. 458 (7240): 859–64. Bibcode:2009Натура.458..859G. Дои:10.1038 / природа07885. ЧВК  2748673. PMID  19370028.
45. Фрей, КМ; Георгиев, I; Дональд, BR; Андерсон, AC (3 августа 2010 г.). «Прогнозирование мутаций устойчивости с помощью алгоритмов дизайна белков». Труды Национальной академии наук Соединенных Штатов Америки. 107 (31): 13707–12. Bibcode:2010PNAS..10713707F. Дои:10.1073 / pnas.1002162107. ЧВК  2922245. PMID  20643959.
46. Хури, Джорджия; Fazelinia, H; Чин, JW; Pantazes, RJ; Чирино, ПК; Маранас, CD (октябрь 2009 г.). «Расчетный дизайн ксилозоредуктазы Candida boidinii для измененной специфичности кофактора». Белковая наука. 18 (10): 2125–38. Дои:10.1002 / pro.227. ЧВК  2786976. PMID  19693930.
47. Бертон, Д.Р .; Вайс, РА (13 августа 2010 г.). «СПИД / ВИЧ. Продвижение разработки вакцины против ВИЧ». Наука. 329 (5993): 770–3. Bibcode:2010Sci ... 329..770B. Дои:10.1126 / science.1194693. PMID  20705840. S2CID  206528638.
48. Джессика Маршалл (7 ноября 2012 г.). «Белки на заказ». Новости природы. Получено 17 ноября, 2012.
49. Разработаны трансмембранные альфа-шпильки-белки. в База данных OPM
50. Разработаны ассоциированные с мембраной пептиды и белки в База данных OPM
51. Чоудхури, Ратул; Кумар, Маниш; Маранас, Костас Д.; Golbeck, John H .; Бейкер, Кэрол; Прабхакар, Дживан; Гризвуд, Мэтью; Деккер, Карл; Шанкла, Маниш (10 сентября 2018 г.). «PoreDesigner для настройки селективности растворенных веществ в прочных и высокопроницаемых порах внешней мембраны». Nature Communications. 9 (1): 3661. Bibcode:2018НатКо ... 9.3661C. Дои:10.1038 / s41467-018-06097-1. ISSN  2041-1723. ЧВК  6131167. PMID  30202038.
52. Looger, Loren L .; Дуайер, Мэри А .; Смит, Джеймс Дж. И Хеллинга, Хомм У. (2003). «Вычислительный дизайн рецепторов и сенсорных белков с новыми функциями». Природа. 423 (6936): 185–190. Bibcode:2003Натура 423..185л. Дои:10.1038 / природа01556. PMID  12736688. S2CID  4387641.
53. Джа, РК; Wu, YI; Zawistowski, JS; МакНевин, К; Хан, км; Кульман, Б. (21 октября 2011 г.). «Редизайн аутоингибиторного домена PAK1 для повышения стабильности и аффинности в биосенсорных приложениях». Журнал молекулярной биологии. 413 (2): 513–22. Дои:10.1016 / j.jmb.2011.08.022. ЧВК  3202338. PMID  21888918.

дальнейшее чтение

• Дональд, Брюс Р. (2011). Алгоритмы структурной молекулярной биологии. Кембридж, Массачусетс: MIT Press.
• Сандер, Крис; Вринд, Геррит; Базан, Фернандо; Горовиц, Амнон; Накамура, Харуки; Рибас, Луис; Финкельштейн, Алексей В .; Локхарт, Эндрю; Меркл, Райнер; и другие. (1992). «Белковый дизайн на компьютерах. Пять новых белков: Шпилка, Грендель, Фингерзап, Кожа и Аида». Белки: структура, функции и биоинформатика. 12 (2): 105–110. Дои:10.1002 / prot.340120203. PMID  1603799. S2CID  38986245.
• Цзинь, Вэньчжэнь; Камбара, Оки; Сасакава, Хироаки; Тамура, Ацуо и Такада, Сёдзи (2003). «Дизайн складываемых белков с гладкой складывающейся воронкой от De Novo: автоматизированный дизайн отрицательных результатов и экспериментальная проверка». Структура. 11 (5): 581–590. Дои:10.1016 / S0969-2126 (03) 00075-3. PMID  12737823.
• Покала, Навин и Гендель, Трейси М. (2005). «Энергетические функции для дизайна белков: корректировка сродства белок-белковых комплексов, модели для развернутого состояния и отрицательный дизайн растворимости и специфичности». Журнал молекулярной биологии. 347 (1): 203–227. Дои:10.1016 / j.jmb.2004.12.019. PMID  15733929.