Механика разрушения - Fracture mechanics

«Микротрещина» перенаправляется сюда. О хирургической технике см. Хирургия микротрещин.

Три режима разрушения

Механика разрушения это область механика занимается изучением распространения трещин в материалах. Использует методы аналитического механика твердого тела для расчета движущей силы на трещине и экспериментальной механики твердого тела для характеристики сопротивления материала перелом.

В современном материаловедение Механика разрушения - важный инструмент, используемый для улучшения характеристик механических компонентов. Он применяет физика из стресс и напряжение поведение материалов, в частности теории эластичность и пластичность, микроскопическим кристаллографические дефекты найдены в реальных материалах, чтобы предсказать макроскопическое механическое поведение этих тел. Фрактография широко используется в механике разрушения, чтобы понять причины отказов, а также проверить теоретические прогнозы отказов с отказами реальной жизни. Прогнозирование роста трещин лежит в основе устойчивость к повреждениям Дисциплина механического проектирования.

Есть три способа приложения силы, чтобы трещина могла распространяться:

• Режим I - Режим открытия (а растягивающее напряжение перпендикулярно плоскости трещины),
• Режим II - Скользящий режим (a напряжение сдвига действует параллельно плоскости трещины и перпендикулярно ее фронту), и
• Режим III - Режим отрыва (напряжение сдвига, действующее параллельно плоскости трещины и параллельно ее фронту).

Мотивация

Процессы изготовления, обработки, механической обработки и формовки материалов могут привести к появлению дефектов в готовом механическом компоненте. Во всех металлических конструкциях обнаруживаются внутренние и внешние дефекты, возникающие в процессе производства. Не все подобные дефекты нестабильны в условиях эксплуатации. Механика разрушения - это анализ дефектов для выявления тех, которые безопасны (то есть не растут), и тех, которые могут распространяться как трещины и, таким образом, вызывать отказ дефектной конструкции. Несмотря на эти врожденные недостатки, можно добиться устойчивость к повреждениям анализ безопасной эксплуатации конструкции. Механика разрушения как предмет критического изучения существует всего лишь столетие, и поэтому она относительно нова.^[1][2]

Механика разрушения должна попытаться дать количественные ответы на следующие вопросы:^[2]

1. Какова прочность компонента в зависимости от размера трещины?
2. Какой размер трещины допустим при эксплуатационной нагрузке, т.е. каков максимально допустимый размер трещины?
3. Сколько времени требуется, чтобы трещина вырастала от определенного начального размера, например минимального обнаруживаемого размера трещины, до максимально допустимого размера трещины?
4. Каков срок службы конструкции, если предполагается, что уже существует определенный размер дефекта (например, производственный дефект)?
5. В течение периода, доступного для обнаружения трещин, как часто следует проверять конструкцию на наличие трещин?

Линейная механика упругого разрушения

Критерий Гриффита

Краевая трещина (дефект) длины ${\displaystyle a}$ в материале

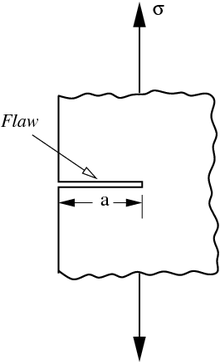
Механика разрушения была разработана во время Первой мировой войны английским авиационным инженером. А. А. Гриффит - таким образом, термин Гриффит трещина - объяснить разрушение хрупких материалов.^[3] Работа Гриффита была мотивирована двумя противоречащими друг другу фактами:

• Напряжение, необходимое для разрушения массы стекло составляет около 100 МПа (15000 фунтов на квадратный дюйм).
• Теоретическое напряжение, необходимое для разрыва атомных связей в стекле, составляет приблизительно 10 000 МПа (1 500 000 фунтов на кв. Дюйм).

Требовалась теория, чтобы согласовать эти противоречивые наблюдения. Кроме того, эксперименты со стеклянными волокнами, которые проводил сам Гриффит, показали, что напряжение разрушения увеличивается с уменьшением диаметра волокна. Следовательно, прочность на одноосное растяжение, которая широко использовалась для прогнозирования разрушения материала до Гриффита, не могла быть независимым от образца свойством материала. Гриффит предположил, что низкая прочность на излом, наблюдаемая в экспериментах, а также зависимость прочности от размера были обусловлены наличием микроскопических дефектов в массивном материале.

Чтобы проверить гипотезу о дефекте, Гриффит ввел искусственный дефект в свои экспериментальные образцы стекла. Искусственный дефект имел форму поверхностной трещины, которая была намного больше, чем другие дефекты в образце. Эксперименты показали, что произведение квадратного корня из длины дефекта (${\displaystyle a}$) и напряжение при разрушении (${\displaystyle \sigma _{f}}$) была почти постоянной, что выражается уравнением:

${\displaystyle \sigma _{f}{\sqrt {a}}\approx C}$

Объяснение этой связи с точки зрения линейной теории упругости проблематично. Теория линейной упругости предсказывает, что напряжение (и, следовательно, деформация) на вершине острого дефекта в линейной эластичный материал бесконечен. Чтобы избежать этой проблемы, Гриффит разработал термодинамический подход, чтобы объяснить связь, которую он наблюдал.

Рост трещины, расширение поверхностей по обе стороны от трещины требует увеличения поверхностная энергия. Гриффит нашел выражение для постоянной ${\displaystyle C}$ через поверхностную энергию трещины путем решения задачи упругости конечной трещины в упругой пластине. Вкратце подход был таков:

• Вычислить потенциальная энергия хранится в идеальном образце под одноосной растягивающей нагрузкой.
• Закрепите границу так, чтобы приложенная нагрузка не действовала, а затем создайте трещину в образце. Трещина ослабляет напряжение и, следовательно, уменьшает упругая энергия возле берегов трещин. С другой стороны, трещина увеличивает общую поверхностную энергию образца.
• Вычислить изменение свободная энергия (поверхностная энергия - упругая энергия) как функция длины трещины. Разрушение происходит, когда свободная энергия достигает пикового значения при критической длине трещины, за пределами которой свободная энергия уменьшается по мере увеличения длины трещины, то есть вызывая разрушение. Используя эту процедуру, Гриффит обнаружил, что

${\displaystyle C={\sqrt {\cfrac {2E\gamma }{\pi }}}}$

куда ${\displaystyle E}$ - модуль Юнга материала и ${\displaystyle \gamma }$ - плотность поверхностной энергии материала. Предполагая ${\displaystyle E=62\ {\text{GPa}}}$ и ${\displaystyle \gamma =1\ {\text{J/m}}^{2}}$ дает превосходное соответствие предсказанного Гриффитса напряжения разрушения с экспериментальными результатами для стекла.

Критерий Гриффита использовался Джонсон, Кендалл и Робертс также применительно к клеевым контактам.^[4] Недавно было показано, что прямое применение критерия Гриффитса к одной числовой «ячейке» приводит к очень надежной формулировке метода граничных элементов.^[5]

Для материалов, сильно деформированных до распространения трещины, формулировка линейной упругой механики разрушения больше не применима, и необходима адаптированная модель для описания поля напряжения и смещения вблизи вершины трещины, например разрушение мягких материалов.

Модификация Ирвина

Пластическая зона вокруг вершины трещины в пластичном материале

Работы Гриффита в значительной степени игнорировались инженерным сообществом до начала 1950-х годов. Причины этого, по-видимому, заключаются в (а) в реальных конструкционных материалах уровень энергии, необходимой для разрушения, на несколько порядков выше, чем соответствующая поверхностная энергия, и (б) в конструкционных материалах всегда есть некоторые неупругие деформации вокруг трещины. фронт, что сделало бы предположение о линейно-упругой среде с бесконечными напряжениями в вершине трещины крайне нереалистичным. ^[6]

Теория Гриффита прекрасно согласуется с экспериментальными данными для хрупкий такие материалы, как стекло. За пластичный материалы, такие как стали, хотя отношение ${\displaystyle \sigma _{f}{\sqrt {a}}=C}$ все еще сохраняется, поверхностная энергия (γ), предсказываемая теорией Гриффита, обычно нереально высока. Группа, работающая под Г. Р. Ирвин^[7] на Лаборатория военно-морских исследований США (NRL) во время Второй мировой войны осознали, что пластичность должна играть важную роль в разрушении пластичных материалов.

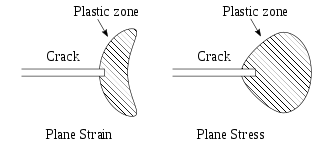
В пластичных материалах (и даже в материалах, которые кажутся хрупкими)^[8]), а пластик зона развивается на вершине трещины. Как применяется нагрузка увеличивается, пластическая зона увеличивается в размере до тех пор, пока трещина не разрастется и упруго деформированный материал за вершиной трещины не разгрузится. Цикл пластического нагружения и разгрузки вблизи вершины трещины приводит к рассеяние из энергия в качестве высокая температура. Следовательно, к уравнению баланса энергии, разработанному Гриффитсом для хрупких материалов, следует добавить диссипативный член. С физической точки зрения для роста трещин в пластичных материалах требуется дополнительная энергия по сравнению с хрупкими материалами.

Стратегия Ирвина заключалась в разделении энергии на две части:

• накопленная энергия упругой деформации, которая высвобождается при росте трещины. Это термодинамическая движущая сила разрушения.
• рассеиваемая энергия, которая включает пластическую диссипацию и поверхностную энергию (и любые другие диссипативные силы, которые могут действовать). Рассеиваемая энергия обеспечивает термодинамическое сопротивление разрушению. Тогда полная энергия равна

${\displaystyle G=2\gamma +G_{p}}$

куда ${\displaystyle \gamma }$ - поверхностная энергия и ${\displaystyle G_{p}}$ - пластическая диссипация (и диссипация от других источников) на единицу площади роста трещины.

Модифицированная версия энергетического критерия Гриффита может быть записана в виде

${\displaystyle \sigma _{f}{\sqrt {a}}={\sqrt {\cfrac {E~G}{\pi }}}.}$

Для хрупких материалов, таких как стекло, термин поверхностной энергии доминирует и ${\displaystyle G\approx 2\gamma =2\,\,{\text{J/m}}^{2}}$. Для пластичных материалов, таких как сталь, преобладает коэффициент рассеяния пластичности и ${\displaystyle G\approx G_{p}=1000\,\,{\text{J/m}}^{2}}$. За полимеры близко к стеклование температуры имеем промежуточные значения ${\displaystyle G}$ от 2 до 1000 ${\displaystyle {\text{J/m}}^{2}}$.

Коэффициент интенсивности стресса

Основная статья: Коэффициент интенсивности стресса

Другим значительным достижением Ирвина и его коллег было обнаружение метода расчета количества энергии, доступной для разрушения, в терминах асимптотических полей напряжений и смещений вокруг фронта трещины в линейном упругом твердом теле.^[7] Это асимптотическое выражение для поля напряжений в режиме нагружения I связано с коэффициент интенсивности напряжений K_я следующий:^[9]

${\displaystyle \sigma _{ij}=\left({\cfrac {K_{I}}{\sqrt {2\pi r}}}\right)~f_{ij}(\theta )}$

куда σ_ij являются Подчеркивает Коши, р расстояние от вершины трещины, θ - угол по отношению к плоскости трещины, а ж_ij - функции, зависящие от геометрии трещины и условий нагружения. Ирвин назвал количество K в коэффициент интенсивности напряжений. Поскольку количество ж_ij безразмерен, коэффициент интенсивности напряжений можно выразить в единицах ${\displaystyle {\text{MPa}}{\sqrt {\text{m}}}}$.

Когда включение жесткой линии Рассмотрено аналогичное асимптотическое выражение для полей напряжений.

Высвобождение энергии деформации

Основная статья: Скорость высвобождения энергии деформации

Ирвин был первым, кто заметил, что если размер пластической зоны вокруг трещины мал по сравнению с размером трещины, энергия, необходимая для роста трещины, не будет критически зависеть от состояния напряжения (пластической зоны) при кончик трещины.^[6] Другими словами, чисто упругое решение можно использовать для расчета количества энергии, доступной для разрушения.

Скорость выделения энергии при росте трещины или скорость высвобождения энергии деформации затем можно рассчитать как изменение энергии упругой деформации на единицу площади роста трещины, т. е.

${\displaystyle G:=\left[{\cfrac {\partial U}{\partial a}}\right]_{P}=-\left[{\cfrac {\partial U}{\partial a}}\right]_{u}}$

куда U - упругая энергия системы и а - длина трещины. Либо нагрузка п или смещение ты постоянны при вычислении вышеуказанных выражений.

Ирвин показал, что режим я взламываю (режим открытия) скорость выделения энергии деформации и коэффициент интенсивности напряжений связаны соотношением:

${\displaystyle G=G_{I}={\begin{cases}{\cfrac {K_{I}^{2}}{E}}&{\text{plane stress}}\\{\cfrac {(1-\nu ^{2})K_{I}^{2}}{E}}&{\text{plane strain}}\end{cases}}}$

куда E это Модуль для младших, ν является Коэффициент Пуассона, и K_я - коэффициент интенсивности напряжений в режиме I. Ирвин также показал, что скорость выделения энергии деформации плоской трещиной в линейном упругом теле может быть выражена через режим I: режим II (скользящий режим) и режим III (режим разрыва) коэффициенты интенсивности напряжений для наиболее общих условий нагружения.

Затем Ирвин принял дополнительное предположение о том, что размер и форма зоны диссипации энергии остаются примерно постоянными во время хрупкого разрушения. Это предположение предполагает, что энергия, необходимая для создания единичной поверхности разрушения, является постоянной величиной, которая зависит только от материала. Это новое свойство материала было названо вязкость разрушения и назначил грамм_IC. Сегодня это критический фактор интенсивности напряжений. K_IC, найденное в условии плоской деформации, которое принято в качестве определяющего свойства в линейно-упругой механике разрушения.

Пластиковая зона кончика трещины

Теоретически напряжение в вершине трещины, радиус которой близок к нулю, стремится к бесконечности. Это будет считаться сингулярностью напряжения, что невозможно в реальных приложениях. По этой причине при численных исследованиях в области механики разрушения часто бывает уместно представлять трещины в виде закругленных концов. выемки с зависимой от геометрии областью концентрации напряжений, заменяющей особенность вершины трещины.^[9] На самом деле было обнаружено, что концентрация напряжений в вершине трещины в реальных материалах имеет конечное значение, но больше номинального напряжения, приложенного к образцу. Уравнение, определяющее напряжения около вершины трещины, приведено ниже:^[10]

${\displaystyle \sigma _{l}=\sigma \left(1+Y{\sqrt {\frac {c\pi }{2\pi r}}}\right)}$

Напряжение около вершины трещины, ${\displaystyle \sigma _{l}}$, зависит от номинального приложенного напряжения, ${\displaystyle \sigma }$ и поправочный коэффициент, ${\displaystyle Y}$ (который зависит от геометрии образца) и обратно зависит от радиального расстояния (${\displaystyle r}$) от вершины трещины. Тем не менее, должен быть какой-то механизм или свойство материала, которое предотвращает самопроизвольное распространение такой трещины. Предполагается, что пластическая деформация в вершине трещины эффективно притупляет вершину трещины. Эта деформация зависит в первую очередь от приложенного напряжения в соответствующем направлении (в большинстве случаев это направление y в регулярной декартовой системе координат), длины трещины и геометрии образца.^[11] Чтобы оценить, как эта зона пластической деформации простиралась от вершины трещины, Ирвин приравнял предел текучести материала к напряжениям в дальней зоне в y-направлении вдоль трещины (x-направление) и рассчитал эффективный радиус. Исходя из этого соотношения и предполагая, что трещина нагружена до критического коэффициента интенсивности напряжений, Ирвин разработал следующее выражение для идеализированного радиуса зоны пластической деформации в вершине трещины:

${\displaystyle r_{p}={\frac {K_{C}^{2}}{2\pi \sigma _{Y}^{2}}}}$

Модели идеальных материалов показали, что эта зона пластичности сосредоточена в вершине трещины.^[12] Это уравнение дает приблизительный идеальный радиус деформации пластической зоны за вершиной трещины, что полезно для многих ученых-строителей, поскольку оно дает хорошую оценку того, как материал ведет себя при воздействии напряжения. В приведенном выше уравнении параметры коэффициента интенсивности напряжений и показателя вязкости материала, ${\displaystyle K_{C}}$, а предел текучести, ${\displaystyle \sigma _{Y}}$, важны, потому что они иллюстрируют многое о материале и его свойствах, а также о размере пластической зоны. Например, если ${\displaystyle K_{c}}$ высокий, то можно сделать вывод, что материал жесткий, тогда как если ${\displaystyle \sigma _{Y}}$ высокий, известно, что материал более пластичный. Соотношение этих двух параметров важно для радиуса пластической зоны. Например, если ${\displaystyle \sigma _{Y}}$ мало, то квадрат отношения ${\displaystyle K_{C}}$ к ${\displaystyle \sigma _{Y}}$ большой, что приводит к большему пластическому радиусу. Это означает, что материал может пластически деформироваться и, следовательно, является жестким.^[11] Эту оценку размера пластической зоны за вершиной трещины можно затем использовать для более точного анализа поведения материала при наличии трещины.

Тот же процесс, что описан выше для загрузки одного события, также применяется и к циклической загрузке. Если трещина присутствует в образце, который подвергается циклическому нагружению, образец будет пластически деформироваться на вершине трещины и замедлить рост трещины. В случае перегрузки или отклонения эта модель слегка изменяется, чтобы приспособиться к внезапному увеличению напряжения по сравнению с тем, которое ранее испытывал материал. При достаточно высокой нагрузке (перегрузке) трещина вырастает из содержащей ее пластической зоны и оставляет после себя карман исходной пластической деформации. Теперь, если предположить, что напряжение перегрузки недостаточно велико для полного разрушения образца, трещина будет подвергаться дальнейшей пластической деформации вокруг вершины новой трещины, увеличивая зону остаточных пластических напряжений. Этот процесс еще больше укрепляет и продлевает срок службы материала, поскольку новая пластическая зона больше, чем она была бы в обычных условиях напряжения. Это позволяет материалу подвергаться большему количеству циклов нагрузки. Эта идея может быть дополнительно проиллюстрирована график алюминия с центральной трещиной, подверженной перегрузкам.^[13]

Испытания на вязкость разрушения

Основная статья: Вязкость разрушения

Ограничения

В SS. Скенектади разделены на хрупкое разрушение в гавани, 1943 год.

Но перед исследователями NRL возникла проблема, потому что военно-морские материалы, например, корабельная листовая сталь, не являются идеально эластичными, но подвергаются значительным воздействиям. Пластическая деформация на кончике трещины. Одно из основных предположений в линейной механике упругого разрушения Ирвина - это мелкомасштабная податливость, условие, согласно которому размер пластической зоны мал по сравнению с длиной трещины. Однако это предположение является весьма ограничительным для определенных типов разрушения конструкционных сталей, хотя такие стали могут быть склонны к хрупкому разрушению, которое привело к ряду катастрофических отказов.

Линейно-упругая механика разрушения имеет ограниченное практическое применение для конструкционных сталей и Вязкость разрушения тестирование может быть дорогостоящим.

Рост трещины

В общем, инициирование и продолжение трескаться рост зависит от нескольких факторов, таких как свойства сыпучего материала, геометрия тела, геометрия трещины, распределение нагрузки, скорость нагрузки, величина нагрузки, условия окружающей среды, временные эффекты (например, вязкоупругость или же вязкопластичность ), и микроструктура.^[14] В этом разделе давайте рассмотрим трещины, которые растут прямо в результате применения нагрузка в результате чего один режим разрушения.

Инициирование пути взлома

По мере роста трещины энергия передается вершине трещины на скорость высвобождения энергии ${\displaystyle G}$, которая является функцией приложенной нагрузки, длины (или площади) трещины и геометрии тело.^[15] Кроме того, все твердые материалы обладают собственной скоростью высвобождения энергии. ${\displaystyle G_{C}}$, куда ${\displaystyle G_{C}}$ называется "энергия разрушения" или "вязкость разрушения "материала.^[15] Трещина будет расти, если выполняется следующее условие

${\displaystyle G\geq G_{C}}$

${\displaystyle G_{C}}$ зависит от множества факторов, таких как температура (в прямом пропорциональный (т.е. чем холоднее материал, тем ниже трещиностойкость и наоборот), наличие плоская деформация или плоское напряжение состояние загрузки, поверхностная энергия характеристики, скорость нагружения, микроструктура, примеси (особенно пустоты), термическая обработка история, и направление роста трещин.^[15]

Устойчивость роста трещин

R-кривые для хрупкого материала и пластичный материал.

Кроме того, по мере роста трещин в теле материала сопротивление материала разрушению увеличивается (или остается постоянным).^[15] Сопротивление материала разрушению может быть уловлено скоростью выделения энергии, необходимой для распространения трещины. ${\displaystyle G_{R}\left(a\right)}$, которая является функцией длины трещины ${\displaystyle a}$. ${\displaystyle G_{R}\left(a\right)}$ зависит от геометрии и микроструктуры материала.^[15] Сюжет о ${\displaystyle G_{R}\left(a\right)}$ против ${\displaystyle a}$ называется кривая сопротивления, или R-образная кривая.

За хрупкий материалы, ${\displaystyle G_{R}}$ постоянное значение, равное ${\displaystyle G_{R0}=G_{C}}$. Для других материалов, ${\displaystyle G_{R}}$ увеличивается с увеличением ${\displaystyle a}$, и он может или не может достичь устойчивое состояние ценить.^[15]

Следующее условие должно быть соблюдено, чтобы трещина имела длину ${\displaystyle a_{0}}$ для увеличения длины небольшой трещины:

${\displaystyle G(a_{0})=G_{R}(a_{0}+\delta a)}$

Тогда условие устойчивого роста трещины:

${\displaystyle {\frac {\delta G(a_{0})}{\delta a}}<{\frac {\delta G_{R}(a_{0})}{\delta a}}}$

И наоборот, условие неустойчивого роста трещины:

${\displaystyle {\frac {\delta G(a_{0})}{\delta a}}\geq {\frac {\delta G_{R}(a_{0})}{\delta a}}}$

Прогнозирование путей трещин

В предыдущем разделе рассматривался только прямолинейный рост трещины от приложения нагрузки, приводящий к единственному режиму разрушения. Однако это явно идеализация; в реальных системах, смешанный режим загрузки (применяется некоторая комбинация загрузки режима I, режима II и режима III). При загрузке в смешанном режиме трещины обычно не продвигаются вперед.^[15] Было предложено несколько теорий для объяснения перегиба трещин и их распространения при смешанном нагружении, две из которых выделены ниже.

Применение равномерного натяжения ${\displaystyle \sigma ~}$на трещине длины ${\displaystyle 2a~}$в бесконечном плоском теле, чтобы вызвать смешанную нагрузку режима I и режима II. Линии твердых тел, идущие от вершин трещин, представляют собой изломы трещин.

Теория максимального кольцевого напряжения

Рассмотрим трещину длиной ${\displaystyle 2a}$ размещенный в бесконечный планарный кузов подвергается смешанным нагрузкам в режимах I и II с помощью равномерных напряжение ${\displaystyle \sigma }$, куда ${\displaystyle \beta }$ - угол между исходной плоскостью трещины и направлением приложенного напряжения и ${\displaystyle \theta ^{\star }}$ - угол между плоскостью исходной трещины и направлением роста трещины изгиба. Сих, Пэрис и Эрдоган показали, что факторы интенсивности стресса вдали от вершин трещин в этой плоской геометрии нагружения просто ${\displaystyle K_{I}=\sigma {\sqrt {\pi a}}\sin ^{2}(\beta )}$ и ${\displaystyle K_{II}=\sigma {\sqrt {\pi a}}\sin(\beta )\cos(\beta )}$.^[16] Кроме того, Эрдоган и Сих^[17] постулированный следующее для этой системы:

1. Расширение трещины начинается с вершины трещины
2. В самолете начинается расширение трещины перпендикуляр в направлении наибольшего напряжения
3. «Критерий максимального напряжения» удовлетворяется, т.е. ${\displaystyle {\sqrt {2\pi r}}\sigma _{\theta }(r,\theta ^{*})\geq K_{Ic}}$, куда ${\displaystyle K_{Ic}}$ - критический коэффициент интенсивности напряжений (и зависит от вязкости разрушения ${\displaystyle G_{C}}$)

Этот постулат подразумевает, что трещина начинает расширяться от вершины в направлении ${\displaystyle \theta ^{\star }}$ вдоль которого растягивающая нагрузка центробежного происхождения ${\displaystyle \sigma _{\theta }}$ максимум.^[17] Другими словами, трещина начинает расширяться от вершины в направлении ${\displaystyle \theta ^{\star }}$ который удовлетворяет следующим условиям:

${\displaystyle {\partial \sigma _{\theta } \over \partial \theta }=0}$ и ${\displaystyle {\partial ^{2}\sigma _{\theta } \over \partial \theta ^{2}}<0}$.

Кольцевое напряжение записывается как

${\displaystyle \sigma _{\theta }={\frac {1}{\sqrt {2\pi r}}}\cos \left({\frac {\theta }{2}}\right)\left[K_{I}\cos ^{2}\left({\frac {\theta }{2}}\right)-{\frac {3}{2}}K_{II}\sin(\theta )\right]}$

куда ${\displaystyle r}$ и ${\displaystyle \theta }$ взяты относительно полярной системы координат, ориентированной на исходную вершину трещины.^[17] Направление расширения трещины ${\displaystyle \theta ^{\star }}$ и конверт неудач (сюжет ${\displaystyle K_{II}{\text{ vs }}K_{I}}$) определяются путем удовлетворения постулируемых критериев. Для чистой загрузки Mode-II, ${\displaystyle \theta ^{\star }}$ рассчитывается как ${\displaystyle 70.5^{\circ }}$.^[17]

Теория максимального кольцевого напряжения достаточно точно предсказывает угол распространения трещины в экспериментальных результатах и ​​дает нижняя граница в конверт неудачи.^[15]

Критерий максимальной скорости выделения энергии

Отрицательный угол перегиба трещины ${\displaystyle -\theta ^{*}~}$угол приложения нагрузки ${\displaystyle \beta ~}$согласно теории максимального кольцевого напряжения. Углы даны в градусах.

Рассмотрим трещину длиной ${\displaystyle 2a}$ размещенный в бесконечно удаленном плоском корпусе, находящемся в состоянии постоянного напряжения режима I и режима II, приложенного бесконечно далеко. При такой нагрузке трещина будет перегибаться с длиной перегиба. ${\displaystyle \epsilon }$ под углом ${\displaystyle \alpha }$ по отношению к исходной трещине. Ву^[18] постулировал, что изгибы трещин будут распространяться под критическим углом ${\displaystyle \alpha =\alpha _{C}}$ который максимизирует скорость высвобождения энергии, указанную ниже. Ву определяет ${\displaystyle U\left({\boldsymbol {\sigma }}\right)}$ и ${\displaystyle U_{z}\left({\boldsymbol {\sigma }},\alpha ,\epsilon \right)}$ быть энергии деформации хранятся в образцах, содержащих прямую трещину и изогнутую трещину (или Z-образную трещину) соответственно.^[18] Скорость высвобождения энергии, которая возникает, когда вершины прямой трещины начинают изгибаться, определяется как

${\displaystyle G\left({\boldsymbol {\sigma }},\alpha \right)={\frac {1}{2}}\lim _{\epsilon \to 0}{\frac {U_{z}-U}{\epsilon }}}$

Таким образом, трещина будет перегибаться и распространяться по критический угол ${\displaystyle \alpha =\alpha _{C}}$ который удовлетворяет следующему критерию максимальной скорости выделения энергии:

${\displaystyle {\partial G \over \partial \alpha }{\bigg |}_{\alpha =\alpha _{C}}=0}$

${\displaystyle {\partial ^{2}G \over \partial \alpha ^{2}}{\bigg |}_{\alpha =\alpha _{C}}\leq 0}$

${\displaystyle G\left({\boldsymbol {\sigma }},\alpha \right)\geq G_{C}}$

${\displaystyle G\left({\boldsymbol {\sigma }},\alpha \right)}$ не может быть выражена как закрытая функция, но это может быть хорошо приблизительный хотя Численное моделирование.^[18]

Для трещин в чистом режиме загрузки II, ${\displaystyle \alpha _{C}}$ рассчитывается как ${\displaystyle 75.6^{\circ }}$, что хорошо согласуется с теорией максимального кольцевого напряжения.^[18]

Анизотропия

Другие факторы также могут влиять на направление роста трещины, например, материал дальнего поля. деформация (например., шею ), наличие микроотделений от дефектов, нанесение сжатие, наличие интерфейса между двумя неоднородный материалы или материал фазы, и материал анизотропия, назвать несколько.^[14]

В анизотропных материалах вязкость разрушения изменяется как ориентация в пределах материальных изменений. Вязкость разрушения анизотропного материала можно определить как ${\displaystyle G_{C}\left(\theta \right)}$, куда ${\displaystyle \theta }$ это некоторая мера ориентации.^[15] Следовательно, трещина будет расти под углом ориентации ${\displaystyle \theta =\theta ^{*}}$ когда выполняются следующие условия

${\displaystyle G\left(\theta ^{*}\right)\geq G_{C}\left(\theta ^{*}\right)}$ и ${\displaystyle {\partial G\left(\theta ^{*}\right) \over \partial \theta }={\partial G_{C}\left(\theta ^{*}\right) \over \partial \theta }}$

Вышеизложенное можно рассматривать как формулировку критерия максимальной скорости выделения энергии для анизотропных материалов.^[15]

Устойчивость пути к трещине

Вышеупомянутые критерии для прогнозирования траектории трещины (а именно теория максимального кольцевого напряжения и критерий максимальной скорости выделения энергии) подразумевают, что ${\displaystyle K_{II}=0}$ удовлетворяется на вершине трещины, поскольку трещина расширяется с непрерывно (или плавно) поворотный путь. Это часто называют критерием локальная симметрия.^[19]

Если путь трещины продолжается с прерывисто резкое изменение направления, затем ${\displaystyle K_{II}=0}$ может не обязательно совпадать с начальным направлением пути изломанной трещины. Но после того, как возник такой перегиб трещины, трещина расширяется так, что ${\displaystyle K_{II}=0}$ доволен.^[19]

Рассмотрим полубесконечный трещина в асимметричный состояние загрузки. Изгиб распространяется от конца этой трещины до точки ${\displaystyle \left(l,\lambda (l)\right)}$ где ${\displaystyle (x,y=\lambda (x))}$ система координат совмещена с предварительно вытянутой вершиной трещины. Коттерелл и Райс применили ${\displaystyle K_{II}=0}$ критерий локальной симметрии для вывода форма первого порядка коэффициентов интенсивности напряжений для вершины изогнутой трещины и формы первого порядка траектории изломанной трещины.^[19]

Коттерелл и рис:[19] Форма первого порядка коэффициентов интенсивности напряжений для изогнутой вершины трещины и форма первого порядка траектории изломанной трещины

Сначала Коттерелл и Райс[19] показали, что коэффициенты интенсивности напряжений для протяженной изогнутой вершины трещины имеют первый порядок ${\displaystyle {\begin{Bmatrix}K_{I}\\K_{II}\end{Bmatrix}}=\left({\frac {2}{\pi }}\right)^{1/2}\int _{-\infty }^{l}\left[{\begin{Bmatrix}T_{y}-\lambda ^{\prime }(l)T_{x}\\T_{x}+\lambda ^{\prime }(l)T_{y}\end{Bmatrix}}{\frac {1}{(l-x)^{1/2}}}+{\begin{Bmatrix}T_{x}\\T_{y}\end{Bmatrix}}{\frac {\left[\lambda (l)-\lambda (x)-\lambda ^{\prime }(l)(l-x)\right]}{2(l-x)^{3/2}}}\right]}$ куда ${\displaystyle T_{x}}$ и ${\displaystyle T_{y}}$ являются тяги на протяженной изогнутой трещине от начала до ${\displaystyle \left(l,\lambda (l)\right)}$. Используя поле напряжений на ${\displaystyle x}$-ось из решения Вильямса,[20] тяги ${\displaystyle T_{x}}$ и ${\displaystyle T_{y}}$ можно записать в первом порядке как ${\displaystyle {\begin{Bmatrix}T_{x}\\T_{y}\end{Bmatrix}}={\frac {1}{\sqrt {2\pi x}}}\left[k_{I}{\begin{Bmatrix}{\frac {\lambda (x)}{2x}}-\lambda ^{\prime }(x)\\1\end{Bmatrix}}+k_{II}{\begin{Bmatrix}1\\{\frac {\lambda (x)}{2x}}-\lambda ^{\prime }(x)\end{Bmatrix}}\right]-{\begin{Bmatrix}\lambda ^{\prime }(x)T\\0\end{Bmatrix}}}$ куда ${\displaystyle k_{I}}$ и ${\displaystyle k_{II}}$ - коэффициенты интенсивности напряжений для предварительно растянутой вершины трещины, ${\displaystyle \lambda ^{\prime }(x)={\operatorname {d} \!\lambda (x) \over \operatorname {d} \!x}}$, и ${\displaystyle T}$ соответствует значению местного напряжения, действующего параллельно к предварительно расширенной вершине трещины, называемой ${\displaystyle T}$ стресс. Например, ${\displaystyle T=-\sigma }$ для прямой трещины под одноосное нормальное напряжение ${\displaystyle \sigma }$.[19] Подставляя тяги в коэффициенты интенсивности напряжений, а затем накладывая ${\displaystyle K_{II}=0}$ критерий локальной симметрии на вершине расширяющейся изгибающейся трещины приводит к следующему интегральное уравнение пути трещины ${\displaystyle y=\lambda (x)}$ ${\displaystyle \theta _{0}=\lambda ^{\prime }(l)-{\frac {\beta }{\pi ^{1/2}}}\int _{0}^{l}{\frac {\lambda ^{\prime }(x)}{(l-x)^{1/2}}}}$ куда ${\displaystyle \beta ={\frac {2{\sqrt {2}}T}{k_{I}}}}$ можно рассматривать как нормализованный ${\displaystyle T}$ стресс и ${\displaystyle \theta _{0}={\frac {-2k_{II}}{k_{I}}}}$ можно рассматривать как начальный угол роста трещины, который обязательно невелик (поэтому приближение малых углов может быть применено). Решение для пути трещины ${\displaystyle \lambda (x)}$ является ${\displaystyle \lambda (x)={\frac {\theta _{0}}{\beta }}\left[\exp(\beta ^{2}x){\text{erfc}}(-\beta x^{1/2})-1-2\beta \left({\frac {x}{\pi }}\right)^{1/2}\right]}$

Решение для пути трещины ${\displaystyle \lambda (x)}$ является

Пути изломанной трещины (штриховые / пунктирные линии), отходящие от полубесконечной трещины (сплошная линия) в асимметричном состоянии нагрузки с ${\displaystyle \theta _{0}=0.2~}$радианы. Обратите внимание на направленно неустойчивый рост трещины для положительного ${\displaystyle \beta ~}$(т.е. для положительного ${\displaystyle T~}$напряжения), нейтрально устойчивый рост трещины при нулевом ${\displaystyle \beta ~}$(т.е. для ${\displaystyle T~}$напряжения), и направленно-устойчивый рост трещины при отрицательных ${\displaystyle \beta ~}$(т.е. при отрицательном ${\displaystyle T~}$стресс).

${\displaystyle \lambda (x)={\frac {\theta _{0}}{\beta }}\left[\exp(\beta ^{2}x){\text{erfc}}(-\beta x^{1/2})-1-2\beta \left({\frac {x}{\pi }}\right)^{1/2}\right]}$

Для малых значений ${\displaystyle \beta ^{2}x}$, решение для пути трещины ${\displaystyle \lambda (x)}$ сводится к следующему разложению в ряд

${\displaystyle \lambda (x)=\theta _{0}x\left[1+{\frac {4T}{3k_{I}}}\left({\frac {2x}{\pi }}\right)^{1/2}+4{\frac {T^{2}x}{k_{I}^{2}}}+\dots \right]}$

Трещина Путь ${\displaystyle \lambda (x)}$Параметры
${\displaystyle \theta _{0}={\frac {-2k_{II}}{k_{I}}}}$ куда ${\displaystyle k_{I}}$ и ${\displaystyle k_{II}}$ коэффициенты интенсивности напряжений для предварительно растянутой вершины трещины
${\displaystyle \beta ={\frac {2{\sqrt {2}}T}{k_{I}}}}$ куда ${\displaystyle T}$ соответствует значению действующего местного напряжения параллельно к предварительно расширенной вершине трещины, называемой ${\displaystyle T}$ стресс
${\displaystyle {\text{erfc}}()}$ это дополнительная функция ошибок

Когда ${\displaystyle T>0}$трещина непрерывно поворачивает все дальше и дальше от своего первоначального пути с увеличением склон по мере его расширения. Это считается направленно неустойчивым ростом изогнутой трещины.^[19] Когда ${\displaystyle T=0}$, путь трещины непрерывно расширяет свой начальный путь. Это считается нейтрально устойчивым ростом изогнутой трещины.^[19] Когда ${\displaystyle T<0}$, трещина постоянно отклоняется от своего первоначального пути с уменьшающимся уклоном и стремится к устойчивой траектории с нулевым уклоном при расширении. Это считается направленно-устойчивым ростом изогнутой трещины.^[19]

Эти теоретические результаты хорошо согласуются (для ${\displaystyle \theta _{0}\leq 15^{\circ }}$) с траекториями трещин, экспериментально наблюдаемыми Радоном, Ливерсом и Калвером в экспериментах на ПММА листы двухосно загружен стрессом ${\displaystyle \sigma }$ нормально к трещине и ${\displaystyle R\sigma }$ параллельно трещине.^[21][22] В этой работе ${\displaystyle T}$ напряжение рассчитывается как ${\displaystyle T=(R-1)\sigma }$.^[19]

После публикации работы Коттерелла и Райса было обнаружено, что положительные ${\displaystyle T}$ напряжение не может быть единственным показателем направленной нестабильности расширения изогнутой трещины. Это утверждение подтверждается Мелином, который показал, что рост трещины является нестабильным по направлению для всех значений ${\displaystyle T}$ напряжение в периодическом (равномерном) множестве трещин.^[23] Кроме того, путь изогнутой трещины и ее направленная устойчивость не могут быть правильно спрогнозированы только с учетом локальных эффектов на краю трещины, как показал Мелин посредством критического анализа решения Коттерелла и Райса для прогнозирования полного пути трещины с изгибом, возникающего из-за постоянного удаленного напряжения ${\displaystyle \tau _{xy}=\tau _{xy}^{\infty }}$.^[24]

Механика упруго-пластического разрушения

Вертикальный стабилизатор, который отделился от Рейс 587 American Airlines, что привело к фатальной аварии

Большинство инженерных материалов демонстрируют нелинейное упругое и неупругое поведение в условиях эксплуатации, связанных с большими нагрузками.^{[нужна цитата ]} В таких материалах могут не выполняться предположения линейной механики упругого разрушения, то есть

• пластическая зона в вершине трещины может иметь размер того же порядка, что и размер трещины.
• размер и форма пластической зоны могут изменяться при увеличении приложенной нагрузки, а также при увеличении длины трещины.

Следовательно, для упругопластических материалов необходима более общая теория роста трещин, которая может учитывать:

• местные условия для начального роста трещины, которые включают зарождение, рост и слияние пустот (декогезию) на вершине трещины.
• критерий глобального энергетического баланса для дальнейшего роста трещин и нестабильного разрушения.

CTOD

Исторически первым параметром для определения вязкости разрушения в упругопластической области был смещение раскрытия вершины трещины (CTOD) или "отверстие на вершине трещины" указано. Этот параметр был определен Уэллсом при исследовании конструкционных сталей, которые из-за высокой вязкости не могли быть охарактеризованы с помощью модели линейной упругой механики разрушения. Он отметил, что до того, как произошло разрушение, стенки трещины уходили^{[требуется разъяснение ]} и что вершина трещины после разрушения была от острой до закругленной из-за пластической деформации. Кроме того, закругление вершины трещины было более выраженным в сталях с превосходной вязкостью.

Есть несколько альтернативных определений CTOD. В двух наиболее распространенных определениях CTOD - это смещение в исходной вершине трещины и пересечение на 90 градусов. Последнее определение было предложено Райсом и обычно используется для вывода CTOD в таких конечно-элементных моделях. Обратите внимание, что эти два определения эквивалентны, если вершина трещины притупляется в виде полукруга.

Большинство лабораторных измерений CTOD было выполнено на образцах с трещинами по краям, нагруженных трехточечным изгибом. В ранних экспериментах использовался плоский лопаточный датчик, который вставлялся в трещину; когда трещина открылась, лопаточный датчик вращался, и на x-y плоттер был отправлен электронный сигнал. Однако этот метод был неточным, так как лопастным датчиком было трудно достичь вершины трещины. Сегодня смещение V в устье трещины измеряется, и CTOD определяется, исходя из предположения, что половины образца жесткие и вращаются вокруг точки шарнира (вершины трещины).

R-кривая

Ранняя попытка в направлении механики упругопластического разрушения была Ирвина кривая сопротивления растяжению трещин, Кривая сопротивления росту трещин или же R-кривая. Эта кривая подтверждает тот факт, что сопротивление разрушению увеличивается с увеличением размера трещины в упругопластических материалах. R-кривая представляет собой график зависимости скорости диссипации полной энергии от размера трещины и может использоваться для изучения процессов медленного устойчивого роста трещины и нестабильного разрушения. Однако R-кривая не использовалась широко в приложениях до начала 1970-х годов. Основные причины, по-видимому, заключаются в том, что R-кривая зависит от геометрии образца, и движущая сила трещины может быть трудно вычислить.^[6]

J-интеграл

Основная статья: J-интеграл

В середине 1960-х гг. Джеймс Р. Райс (тогда в Брауновский университет ) и Г. П. Черепанов независимо друг от друга разработали новую меру ударной вязкости для описания случая, когда деформация вершины трещины настолько велика, что деталь больше не подчиняется линейно-упругому приближению. Анализ Райса, который предполагает нелинейное упругое (или монотонное теория деформации пластик ) деформация перед вершиной трещины обозначается J-интеграл.^[25] Этот анализ ограничен ситуациями, когда пластическая деформация в вершине трещины не распространяется до самого дальнего края нагруженной части. Это также требует, чтобы предполагаемое нелинейное упругое поведение материала было разумным приближением по форме и величине к реальной нагрузочной реакции материала. Параметр упругопластического разрушения обозначен J_IC и условно конвертируется в K_IC используя уравнение (3.1) приложения к статье. Также обратите внимание, что подход J-интеграла сводится к теории Гриффитса для линейно-упругого поведения.

Математическое определение J-интеграла выглядит следующим образом:

${\displaystyle J=\int _{\Gamma }(w\,dy-T_{i}{\frac {\partial u_{i}}{\partial x}}\,ds)\quad {\text{with}}\quad w=\int _{0}^{\varepsilon _{ij}}\sigma _{ij}\,d\varepsilon _{ij}}$

куда

${\displaystyle \Gamma }$ - произвольный путь по часовой стрелке вокруг вершины трещины,

${\displaystyle w}$ - плотность энергии деформации,

${\displaystyle T_{i}}$ компоненты векторов тяги,

${\displaystyle u_{i}}$ компоненты векторов смещения,

${\displaystyle ds}$ инкрементная длина по пути ${\displaystyle \Gamma }$, и

${\displaystyle \sigma _{ij}}$ и ${\displaystyle \varepsilon _{ij}}$ - тензоры напряжений и деформаций.

Модели когезионных зон

Когда значительная область вокруг вершины трещины подверглась пластической деформации, можно использовать другие подходы для определения возможности дальнейшего расширения трещины и направления ее роста и ветвления. Простая техника, которую легко включить в численные расчеты, - это модель когезионной зоны метод, который основан на концепциях, предложенных независимо Баренблатт^[26] и Дагдейл^[27] в начале 1960-х гг. Связь между моделями Дагдейла-Баренблатта и теорией Гриффита впервые обсуждалась Уиллис в 1967 г.^[28] Эквивалентность двух подходов в контексте хрупкого разрушения была показана Рис в 1968 г.^[25] Интерес к моделированию трещин в когезионных зонах возродился с 2000 г. после новаторской работы динамическое разрушение Сюй и Needleman,^[29] и Камачо и Ортис.^[30]

Диаграмма оценки отказов (FAD)

Диаграмма оценки отказов (FAD) - это распространенный метод упругопластического анализа.^[31] Одним из основных преимуществ этого метода является его простота. Место разрушения определяется для материала с использованием основных механических свойств. Коэффициент безопасности может быть рассчитан путем определения отношений приложенного напряжения к пределу текучести и интенсивности приложенного напряжения к вязкости разрушения, а затем сравнения этих отношений с местом разрушения.

Размер переходного дефекта

Напряжение разрушения как функция размера трещины

Пусть у материала есть предел текучести ${\displaystyle \sigma _{Y}}$ и трещиностойкость в режиме I ${\displaystyle K_{Ic}}$. Основываясь на механике разрушения, материал разрушается при напряжении. ${\displaystyle \sigma _{\text{fail}}=K_{Ic}/{\sqrt {\pi a}}}$. Исходя из пластичности, материал поддается при ${\displaystyle \sigma _{fail}=\sigma _{Y}}$. Эти кривые пересекаются при ${\displaystyle a=K_{Ic}^{2}/\pi \sigma _{Y}^{2}}$. Это значение ${\displaystyle a}$ называется как размер переходного дефекта ${\displaystyle a_{t}}$., и зависит от свойств материала конструкции. Когда ${\displaystyle a<a_{t}}$, разрушение определяется пластической текучестью, а когда ${\displaystyle a>a_{t}}$ разрушение регулируется механикой разрушения. Значение ${\displaystyle a_{t}}$ для технических сплавов - 100 мм, для керамики - 0,001 мм.^{[нужна цитата ]} Если предположить, что производственные процессы могут приводить к дефектам в порядке микрометры, то можно видеть, что керамика с большей вероятностью разрушится в результате разрушения, тогда как технические сплавы разрушатся в результате пластической деформации.

Ограничение кончика трещины при большой текучести

В условиях мелкомасштабной текучести один параметр (например, K, J или CTOD) характеризует состояние вершины трещины и может использоваться в качестве критерия разрушения, не зависящего от геометрии. Однопараметрическая механика разрушения нарушается при наличии чрезмерной пластичности и когда вязкость разрушения зависит от размера и геометрии испытуемого образца. Теории, используемые для крупномасштабной добычи, не очень стандартизированы. Следующие теории и подходы обычно используются исследователями в этой области.^{[нужна цитата ]}

Теория JQ

Теория JQ, первоначально предложенная О'Даудом и Ши,^[32] использует меру кончика трещины трехосность напряжений, ${\displaystyle Q}$, чтобы охарактеризовать поля вершины трещины при большой текучести. Используя МКЭ, можно установить Q, чтобы изменить поле напряжений для лучшего решения, когда пластическая зона растет.^[32] Новое поле напряжений:^[33]

${\displaystyle \sigma _{ij}=(\sigma _{ij})_{HRR}+Q\delta _{ij}\sigma _{\text{y}}}$

куда ${\displaystyle \delta _{ij}=1}$ за ${\displaystyle i=j}$ и 0, если нет^{[нужна цитата ]}, ${\displaystyle (\sigma _{ij})_{HRR}}$ поле Хатчинсона-Райса-Розенгрена, и ${\displaystyle \sigma _{y}}$ предел текучести.

Q обычно принимает значения от −3 до +2. Отрицательное значение сильно меняет геометрию пластической зоны.

Теория J-Q-M включает в себя еще один параметр, параметр несовпадения, который используется для сварных швов, чтобы компенсировать изменение ударной вязкости металла шва (WM), основного металла (BM) и зоны термического влияния (HAZ). Это значение интерпретируется в формуле аналогично Q-параметру, и обычно предполагается, что эти два параметра не зависят друг от друга.

Т-срок эффекты

В качестве альтернативы теории JQ можно использовать параметр T. Это изменяет только нормальное напряжение в x-направлении (и z-направлении в случае плоской деформации). T не требует использования FEM, но является производным от ограничения. Можно утверждать, что T ограничивается LEFM, но, поскольку изменение пластической зоны из-за T никогда не достигает фактической поверхности трещины (за исключением вершины), его справедливость сохраняется не только при мелкомасштабной текучести. Параметр T также существенно влияет на возникновение разрушения в хрупких материалах с использованием критерия разрушения максимальной тангенциальной деформации, как обнаружили исследователи Техасский университет A&M.^[34] Обнаружено, что как параметр T, так и Коэффициент Пуассона материала играют важную роль в прогнозировании угла распространения трещины и вязкости разрушения материалов в смешанном режиме.

Инженерные приложения

Следующая информация необходима для прогнозирования отказа с помощью механики разрушения:

• Приложенная нагрузка
• Остаточный стресс
• Размер и форма детали
• Размер, форма, расположение и ориентация трещины

Обычно не вся эта информация доступна, поэтому приходится делать консервативные предположения.

Иногда проводится посмертный анализ механики трещин. При отсутствии экстремальной перегрузки причины - либо недостаточная ударная вязкость (K_IC) или чрезмерно большая трещина, которая не была обнаружена при плановом осмотре.

Приложение: математические отношения

Критерий Гриффита

Для простого случая тонкой прямоугольной пластины с трещиной, перпендикулярной нагрузке, скорость выделения энергии ${\displaystyle G}$, становится:

${\displaystyle G={\frac {\pi \sigma ^{2}a}{E}}\,}$                 (1.1)

куда ${\displaystyle \sigma }$ приложенное напряжение, ${\displaystyle a}$ составляет половину длины трещины, а ${\displaystyle E}$ это Модуль для младших, которую для случая плоской деформации следует разделить на коэффициент жесткости пластины ${\displaystyle (1-\nu ^{2})}$. Скорость выделения энергии деформации физически можно понять как: скорость, с которой энергия поглощается ростом трещины.

Однако у нас также есть это:

${\displaystyle G_{c}={\frac {\pi \sigma _{f}^{2}a}{E}}\,}$                 (1.2)

Если ${\displaystyle G}$ ≥ ${\displaystyle G_{c}}$, это критерий, при котором трещина начнет распространяться.

Модификации Ирвина

В конце концов из этой работы возникла модификация теории твердого тела Гриффита; термин называется интенсивность стресса скорость высвобождения энергии деформации заменена термином, называемым вязкость разрушения заменила поверхностную слабость энергии. Оба этих термина просто связаны с энергетическими терминами, которые использовал Гриффит:

${\displaystyle K_{I}=\sigma {\sqrt {\pi a}}\,}$                 (2.1)

и

${\displaystyle K_{c}={\sqrt {EG_{c}}}\,}$ (за плоское напряжение )                 (2.2)

${\displaystyle K_{c}={\sqrt {\frac {EG_{c}}{1-\nu ^{2}}}}\,}$ (за плоская деформация )                 (2.3)

куда ${\displaystyle K_{I}}$ это интенсивность стресса, ${\displaystyle K_{c}}$ трещиностойкость, и ${\displaystyle \nu }$ коэффициент Пуассона. Важно признать тот факт, что параметр разрушения ${\displaystyle K_{c}}$ имеет разные значения при измерении при плоском напряжении и плоской деформации

Перелом происходит при ${\displaystyle K_{I}\geq K_{c}}$. Для частного случая плоской деформации деформации ${\displaystyle K_{c}}$ становится ${\displaystyle K_{Ic}}$ и считается материальной собственностью. Нижний индекс I возникает из-за различные способы загрузки материала, чтобы трещина могла распространяться. Это относится к так называемому «режиму I» загрузки в отличие от режима II или III:

Выражение для ${\displaystyle K_{I}}$ в уравнении 2.1 будет отличаться для геометрий, отличных от бесконечной пластины с трещинами в центре, как обсуждалось в статье о коэффициенте интенсивности напряжений. Следовательно, необходимо ввести безразмерный поправочный коэффициент, Y, чтобы охарактеризовать геометрию. Этот поправочный коэффициент, также часто называемый коэффициент геометрической формы, дается эмпирически определенным рядом и учитывает тип и геометрию трещины или надреза. Таким образом, мы имеем:

${\displaystyle K_{I}=Y\sigma {\sqrt {\pi a}}\,}$                 (2.4)

куда Y является функцией длины трещины и ширины данного листа для листа конечной ширины W содержащая сквозную трещину длиной 2а, к:

${\displaystyle Y\left({\frac {a}{W}}\right)={\sqrt {\sec \left({\frac {\pi a}{W}}\right)}}\,}$                 (2.5)

Для листа конечной ширины W содержащая сквозную краевую трещину длиной акоэффициент геометрической формы получается как: ^[9]

${\displaystyle Y\left({\frac {a}{W}}\right)=1.12-{\frac {0.41}{\sqrt {\pi }}}{\frac {a}{W}}+{\frac {18.7}{\sqrt {\pi }}}\left({\frac {a}{W}}\right)^{2}-\cdots \,}$                 (2.6)

Эластичность и пластичность

Поскольку инженеры привыкли использовать K_IC для характеристики вязкости разрушения использовалось соотношение для уменьшения J_IC к нему:

${\displaystyle K_{Ic}={\sqrt {E^{*}J_{Ic}}}\,}$ куда ${\displaystyle E^{*}=E}$ для плоского напряжения и ${\displaystyle E^{*}={\frac {E}{1-\nu ^{2}}}}$ для плоской деформации (3.1)

Остальная часть математики, используемой в этом подходе, интересна, но, вероятно, лучше изложена на внешних страницах из-за ее сложной природы.

Карты механизма разрушения

Карта механизма разрушения представляет собой диаграмму, построенную по эмпирическим данным разрушения с гомологической температурой T / Tm по горизонтальной оси, где Tm - температура плавления, и нормированным растягивающим напряжением σn / E по вертикальной оси, где σn - это температура плавления. номинальное напряжение, а E - модуль Юнга. Эта карта представляет доминирующий механизм разрушения материала с контурами времени до разрушения и деформации до разрушения. путем сравнения механизмов с наименьшим значением времени до разрушения, которое быстрее всего приводит к отказу. ^[35]

Микромеханизм перелома

Расщепление

При достаточно низкой температуре трещина обычно преобладает над трещиной для большинства кристаллических твердых тел, поскольку температура ограничивает пластичность материала и делает его хрупким. Как правило, раскол контролируется зарождением и распространением трещин, каждая из которых может определять напряжение, при котором образец разрушается.^[36]

Вязкое разрушение при низкой температуре

Вязкое разрушение требует образования дырок при включении, которое концентрирует напряжение. Приложенное напряжение и пластическая деформация вызывают рост отверстий, и когда они становятся достаточно большими, происходит их укрупнение и материал разрушается.

Трансгранулярный перелом ползучести

Этот механизм возникает, когда температура превышает 0,3Tm, и является адаптацией низкотемпературного вязкого разрушения, но следует степенному закону скорости деформации, в котором ползучесть стабилизирует поток и тем самым откладывает слияние отверстий.

Перелом межзеренной ползучести

При низком напряжении механизм разрушения переходит от межзеренного к межзеренному, что зависит от пустот и роста трещин на границах зерен. Этот режим определяется диффузией и степенной ползучестью, поскольку небольшие пустоты растут за счет диффузии на границе зерен, но пространство между пустотами контролируется деформационной ползучестью.

Диффузный перелом

При очень низких напряжениях и высоких температурах диффузионное поле преобладает над растущими пустотами, и ползучесть по степенному закону незначительна.

Разрыв

При очень высоких температурах высокие скорости восстановления снимают напряжение при включении и подавляют зарождение внутренних пустот. Таким образом, без вмешательства другого механизма разрушения деформация продолжается до тех пор, пока площадь поперечного сечения не станет равной нулю.^[37]

Смотрите также

• AFGROW - Программное обеспечение для механики разрушения и анализа роста усталостных трещин
• Анализ разрушения бетона - Изучение механики разрушения бетона
• Землетрясение - Сотрясение поверхности земли, вызванное внезапным выделением энергии в коре
• Усталость - Ослабление материала из-за различных приложенных нагрузок
• Разлом (геология) - Разрыв или разрыв в породе, по которым произошло смещение
• Notch (инженерия)
• Перидинамика, численный метод решения задач механики разрушения
• Удар (механика) - Внезапное кратковременное ускорение
• Сопротивление материалов - Поведение твердых предметов при нагрузках и деформациях
• Коррозионное растрескивание под напряжением - Рост трещин в агрессивной среде
• Структурная механика разрушения - Область проектирования конструкций, связанная с несущими конструкциями с одним или несколькими вышедшими из строя или поврежденными компонентами

Рекомендации

1. T.L. Андерсон (1995). Механика разрушения: основы и приложения. CRC Press. ISBN  978-0849316562.
2. Х. Л. Эвальдс; R.J.H. Уонхилл (1984). Механика разрушения. Эдвард Арнольд и Делфтсе Уитгеверс Маатшаппий. ISBN  978-0-7131-3515-2.
3. Гриффит, А.А. (1921), «Явления разрыва и течения в твердых телах» (PDF), Философские труды Лондонского королевского общества, А, 221 (582–593): 163–198, Bibcode:1921РСПТА.221..163Г, Дои:10.1098 / рста.1921.0006, заархивировано из оригинал (PDF) на 2006-10-16.
4. Johnson, K. L .; Kendall, K .; Робертс, А. Д. (1971-09-08). «Поверхностная энергия и контакт упругих тел». Proc. R. Soc. Лондон. А. 324 (1558): 301–313. Bibcode:1971RSPSA.324..301J. Дои:10.1098 / rspa.1971.0141. ISSN  0080-4630. S2CID  137730057.
5. Попов Валентин Л .; Похрт, Роман; Ли, Цян (2017-09-01). «Прочность клеевых контактов: влияние геометрии контакта и градиента материала». Трение. 5 (3): 308–325. Дои:10.1007 / s40544-017-0177-3. ISSN  2223-7690. S2CID  44025663.
6. Э. Эрдоган (2000) Механика разрушения, Международный журнал твердых тел и структур, 37, стр. 171–183.
7. Ирвин Г (1957), Анализ напряжений и деформаций вблизи конца трещины, пересекающей пластину, Журнал прикладной механики 24, 361–364.
8. Орован, Э., 1949. Разрушение и прочность твердых тел. Доклады о прогрессе физики XII, 185–232.
9. Лю, М .; и другие. (2015). «Усовершенствованное полуаналитическое решение для измерения напряжений в пазах с закругленными концами» (PDF). Инженерная механика разрушения. 149: 134–143. Дои:10.1016 / j.engfracmech.2015.10.004.
10. Алиреза Багер Шемирани; Хаэри, Х. (2017), «Обзорная статья об экспериментальных исследованиях поведения при отказе неустойчивого сустава», Геомеханика и инженерия, 13 (4): 535–570, Дои:10.12989 / gae.2017.13.4.535
11. Вайсхаар, Терри (28 июля 2011 г.). Аэрокосмические конструкции - введение в фундаментальные проблемы. Вест-Лафайет, Индиана: Университет Пердью.
12. «Размер пластической зоны на конце трещины». Справочник по конструкции, устойчивой к повреждениям. LexTech, Inc. Получено 20 ноября 2016.
13. «Замедление». Справочник по конструкции, устойчивой к повреждениям. LexTech, Inc. Получено 20 ноября 2016.
14. Броберг, К. Б. (1999). Трещины и перелом. Сан-Диего: Academic Press. ISBN  0121341305. OCLC  41233349.
15. Зендер, Алан Т. (2012). «Механика разрушения». Конспект лекций по прикладной и вычислительной механике. 62. Дои:10.1007/978-94-007-2595-9. ISBN  978-94-007-2594-2. ISSN  1613-7736.
16. Sih, G.C .; Paris, P.C .; Эрдоган, Ф. (1962). «Кончик трещины, факторы интенсивности напряжений для задач растяжения и изгиба пластин». Журнал прикладной механики. 29 (2): 306. Bibcode:1962JAM .... 29..306S. Дои:10.1115/1.3640546.
17. Эрдоган, Ф .; Сих, Г. К. (1963). «О расширении трещин в пластинах при плоском нагружении и поперечном сдвиге». Журнал фундаментальной инженерии. 85 (4): 519. Дои:10.1115/1.3656897.
18. Ву, Чиен Х. (1978-07-01). «Критерий максимальной скорости выделения энергии, применяемый к образцу растяжения-сжатия с трещиной». Журнал эластичности. 8 (3): 235–257. Дои:10.1007 / BF00130464. ISSN  1573-2681. S2CID  120874661.
19. Cotterell, B .; Райс, Дж. Р. (1980-04-01). «Слегка изогнутые или изогнутые трещины». Международный журнал переломов. 16 (2): 155–169. Дои:10.1007 / BF00012619. ISSN  1573-2673. S2CID  122858531.
20. Уильямс, М. Л. (1957). "N / A". Журнал прикладной механики. 24: 109–114.
21. Radon, J.C .; Leevers, P.S .; Калвер, Л. (1976). «Траектории разрушения в двухосно напряженной пластине». J. Mech. Phys. Твердые тела. 24 (6): 381–395. Bibcode:1976JMPSo..24..381L. Дои:10.1016/0022-5096(76)90010-7.
22. Radon, J.C .; Leevers, P.S .; Калвер, Л. «Вязкость разрушения ПММА при двухосном напряжении». Перелом. 3: 1113–1118.
23. Мелин, Сольвейг (1983-09-01). «Почему трещины избегают друг друга?». Международный журнал переломов. 23 (1): 37–45. Дои:10.1007 / BF00020156. ISSN  1573-2673. S2CID  137031669.
24. Мелин, С. (01.04.2002). «Влияние Т-напряжения на устойчивость трещин по направлению». Международный журнал переломов. 114 (3): 259–265. Дои:10.1023 / А: 1015521629898. ISSN  1573-2673. S2CID  119628924.
25. Райс, Дж. Р. (1968), «Интеграл, не зависящий от траектории, и приближенный анализ концентрации деформаций по надрезам и трещинам» (PDF), Журнал прикладной механики, 35 (2): 379–386, Bibcode:1968JAM .... 35..379R, CiteSeerX  10.1.1.1023.7604, Дои:10.1115/1.3601206.
26. Баренблатт, Г. И. (1962), "Математическая теория равновесных трещин при хрупком разрушении", Успехи прикладной механики, 7: 55–129, Дои:10.1016 / с0065-2156 (08) 70121-2, ISBN  9780120020072
27. Дагдейл, Д. С. (1960), "Податливость стальных листов, содержащих щели", Журнал механики и физики твердого тела, 8 (2): 100–104, Bibcode:1960JMPSo ... 8..100D, Дои:10.1016/0022-5096(60)90013-2
28. Уиллис, Дж. Р. (1967), "Сравнение критериев разрушения Гриффита и Баренблатта", Журнал механики и физики твердого тела, 15 (3): 151–162, Bibcode:1967JMPSo..15..151W, Дои:10.1016/0022-5096(67)90029-4.
29. Xu, X.P .; Нидлман, А. (1994), "Численное моделирование быстрого роста трещин в хрупких твердых телах", Журнал механики и физики твердого тела, 42 (9): 1397–1434, Bibcode:1994JMPSo..42.1397X, Дои:10.1016/0022-5096(94)90003-5
30. Камачо, Г. Т .; Ортис, М. (1996), "Вычислительное моделирование ударных повреждений хрупких материалов", Международный журнал твердых тел и структур, 33 (20–22): 2899–2938, Дои:10.1016/0020-7683(95)00255-3
31. «Механика разрушения».
32. O'Dowd, N.P .; Ши, К. Ф. (1991-01-01). «Семейство полей в вершине трещины, характеризующееся параметром трехосности - I. Структура полей». Журнал механики и физики твердого тела. 39 (8): 989–1015. Дои:10.1016 / 0022-5096 (91) 90049-Т. ISSN  0022-5096.
33. Собойджо, В. О. (2003). «11.7.4 Двухпараметрический J-Q». Механические свойства инженерных материалов. Марсель Деккер. ISBN  0-8247-8900-8. OCLC  300921090.
34. Мирсаяр, М. М., «Анализ разрушения в смешанном режиме с использованием расширенного критерия максимальной тангенциальной деформации», Материалы и дизайн, 2015, DOI: 10.1016 / j.matdes.2015.07.135.
35. Эшби, М. Ф .; Ганди, С .; Таплин, Д. М. Р. (1 мая 1979 г.). «Обзор № 3 Карты механизма разрушения и их построение для металлов и сплавов с ГЦК». Acta Metallurgica. 27 (5): 699. Дои:10.1016/0001-6160(79)90105-6. ISSN  0001-6160.
36. Гриффит, Алан Арнольд; Тейлор, Джеффри Ингрэм (1 января 1921 г.). «VI. Явления разрыва и течения в твердых телах». Философские труды Лондонского королевского общества. Серия A, содержащая статьи математического или физического характера. 221 (582–593): 163–198. Дои:10.1098 / рста.1921.0006.
37. Teirlinck, D .; Zok, F .; Embury, J.D .; Эшби, М. Ф. (1 мая 1988 г.). «Карты механизма разрушения в пространстве напряжений». Acta Metallurgica. 36 (5): 1213–1228. Дои:10.1016 / 0001-6160 (88) 90274-Х. ISSN  0001-6160.

Библиография

• Бакли, К. «Материальный провал», конспект лекций (2005 г.), Оксфордский университет.

дальнейшее чтение

• Дэвидж Р.В., Механическое поведение керамики, Cambridge Solid State Science Series, (1979)
• Демаид, Адриан, Отказоустойчивый, Открытый университет (2004 г.)
• Грин, Д., Введение в механические свойства керамики, Cambridge Solid State Science Series, Eds. Кларк Д.Р., Суреш С., Уорд И.М. (1998)
• Газон, Б.Р., Разрушение хрупких тел, Cambridge Solid State Science Series, 2nd Edn. (1993)
• Фараманд, Б., Бократ, Г. и Гласско Дж. (1997) Механика усталости и разрушения деталей повышенного риска, Чепмен и Холл. ISBN  978-0-412-12991-9.
• Чен, X., Май, Y.-W., Механика разрушения электромагнитных материалов: нелинейная теория поля и приложения, Imperial College Press, (2012)
• А.Н. Гент, W.V. Марс, В: Джеймс Э. Марк, Бурак Эрман и Майк Роланд, редактор (ы), Глава 10 - Прочность эластомеров, Наука и технология резины, Четвертое издание, Academic Press, Бостон, 2013 г., стр. 473–516, ISBN  9780123945846, 10.1016 / B978-0-12-394584-6.00010-8
• Zehnder, Алан. Механика разрушения, SpringerLink, (2012).

внешняя ссылка

• Веб-сайт AFGROW Веб-сайт приложения AFGROW
• Механика разрушения на сайте eFunda
• Примечания к нелинейной механике разрушения Профессор Джон Хатчинсон, Гарвардский университет
• Замечания о разрушении тонких пленок и многослойных материалов Профессор Джон Хатчинсон, Гарвардский университет
• Механика разрушения Профессор Пит Шреурс, Технический университет Эйндховена, Нидерланды
• Fracturemechanics.org Доктор Боб МакГинти, Университет Мерсера
• Примечания к курсу механики разрушения проф. Руи Хуанг, Univ. Техаса
• Применение механики разрушения на keytometals.com