Напряжение сдвига - Shear stress

Напряжение сдвига
Общие символы	τ
Единица СИ	паскаль
Производные от другие количества	τ = F/А

Сила сдвига прилагается к верхней части прямоугольника, в то время как нижняя часть удерживается на месте. Результирующее напряжение сдвига, τ, деформирует прямоугольник в параллелограмм. Задействованная область будет вершиной параллелограмма.

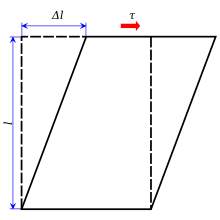
Напряжение сдвига, часто обозначаемый τ (Греческий: тау ), является составляющей стресс копланарны с поперечным сечением материала. Это возникает из сдвигающая сила, составляющая сила вектор параллельно к поперечное сечение материала. Нормальный стресс, с другой стороны, возникает из-за компоненты вектора силы перпендикуляр к сечению материала, на которое он действует.

Общее напряжение сдвига

Формула для расчета среднего напряжения сдвига - это сила на единицу площади:^[1]

${\displaystyle \tau ={F \over A},}$

куда:

τ = напряжение сдвига;

F = приложенная сила;

А = площадь поперечного сечения материала с площадью, параллельной вектору приложенной силы.

Другие формы

Чистый

Чистый сдвиг стресс связан с чистым деформация сдвига, обозначенный γ, по следующему уравнению:^[2]

${\displaystyle \tau =\gamma G\,}$

куда грамм это модуль сдвига из изотропный материал, предоставленный

${\displaystyle G={\frac {E}{2(1+\nu )}}.}$

Здесь E является Модуль для младших и ν является Коэффициент Пуассона.

Сдвиг балки

Сдвиг балки определяется как внутреннее напряжение сдвига балки, вызванное силой сдвига, приложенной к балке.

${\displaystyle \tau ={fQ \over Ib},}$

куда

ж = общая сила сдвига в рассматриваемом месте;

Q = статический момент площади;

б = толщина (ширина) материала перпендикулярно к сдвигу;

я = Момент инерции всей площади поперечного сечения.

Формула сдвига балки также известна как формула напряжения сдвига Журавского после Дмитрий Иванович Журавский который вывел его в 1855 году.^[3][4]

Полумонококовые ножницы

Дальнейшая информация: Сдвиговый поток

Напряжения сдвига в пределах полумонокок конструкция может быть рассчитана путем идеализации поперечного сечения конструкции в виде набора стрингеров (несущих только осевые нагрузки) и перемычек (несущих только сдвиговые потоки ). Разделение сдвигового потока на толщину данной части полумонококовой конструкции дает напряжение сдвига. Таким образом, максимальное напряжение сдвига будет возникать либо в стенке с максимальным сдвиговым потоком, либо с минимальной толщиной.

Также конструкции в грунте могут разрушиться из-за сдвига; например, вес заполненного землей плотина или же дамба может вызвать обрушение недр, как небольшой оползень.

Ударный сдвиг

Максимальное напряжение сдвига, создаваемое в сплошном круглом стержне, подверженном удару, определяется по формуле:

${\displaystyle \tau ={\sqrt {2UG \over V}},}$

куда

U = изменение кинетической энергии;

грамм = модуль сдвига;

V = объем стержня;

и

U = U_{вращающийся} + U_{применяемый};

U_{вращающийся} = 1/2Iω²;

U_{применяемый} = Tθ_{перемещенный};

я = момент инерции массы;

ω = угловая скорость.

Напряжение сдвига в жидкостях

Смотрите также: Вязкость, Поток Куэтта, Уравнение Хагена-Пуазейля, Произведение глубины-уклона, и Простой сдвиг

Любая настоящая жидкости (жидкости и газы Включено) при движении вдоль твердой границы возникнет напряжение сдвига на этой границе. В условие противоскольжения^[5] диктует, что скорость жидкости на границе (относительно границы) равна нулю; хотя на некоторой высоте от границы скорость потока должна равняться скорости жидкости. Область между этими двумя точками называется пограничный слой. Для всех Ньютоновские жидкости в ламинарный поток, напряжение сдвига пропорционально скорость деформации в жидкости, где вязкость - постоянная пропорциональности. За неньютоновские жидкости, то вязкость не является постоянным. Напряжение сдвига передается на границу в результате этой потери скорости.

Для ньютоновской жидкости напряжение сдвига на элементе поверхности, параллельном плоской пластине, в точке у дан кем-то:

${\displaystyle \tau (y)=\mu {\frac {\partial u}{\partial y}}}$

куда

μ это динамическая вязкость потока;

ты это скорость потока по границе;

у высота над границей.

В частности, напряжение сдвига стенки определяется как:

${\displaystyle \tau _{\mathrm {w} }\equiv \tau (y=0)=\mu \left.{\frac {\partial u}{\partial y}}\right|_{y=0}~~.}$

Основной закон Ньютона для любой общей геометрии (включая плоскую пластину, упомянутую выше) утверждает, что тензор сдвига (тензор второго порядка) пропорционален скорости потока градиент (скорость - вектор, поэтому ее градиент - тензор второго порядка):

${\displaystyle \mathbf {\tau } ({\vec {u}})=\mu \nabla {\vec {u}}}$

а константа пропорциональности называется динамическая вязкость. Для изотропного ньютоновского потока это скаляр, а для анизотропного ньютоновского потока он также может быть тензором второго порядка. Фундаментальный аспект состоит в том, что для ньютоновской жидкости динамическая вязкость не зависит от скорости потока (т. Е. Основной закон напряжения сдвига имеет вид линейный), в то время как неньютоновские потоки это неверно, и следует учитывать изменение:

${\displaystyle \mathbf {\tau } ({\vec {u}})=\mu ({\vec {u}})\nabla {\vec {u}}}$

Вышеупомянутая формула больше не является законом Ньютона, а является общим тензорным тождеством: всегда можно найти выражение вязкости как функции скорости потока при любом выражении напряжения сдвига как функции скорости потока. С другой стороны, учитывая напряжение сдвига как функцию скорости потока, оно представляет ньютоновский поток только в том случае, если его можно выразить как постоянную для градиента скорости потока. Константа, которую можно найти в этом случае, - это динамическая вязкость потока.

Пример

Рассматривая двумерное пространство в декартовых координатах (x, y) (компоненты скорости потока соответственно (u, v)), матрица касательных напряжений определяется выражением:

${\displaystyle {\begin{pmatrix}\tau _{xx}&\tau _{xy}\\\tau _{yx}&\tau _{yy}\end{pmatrix}}={\begin{pmatrix}x{\frac {\partial u}{\partial x}}&0\\0&-t{\frac {\partial v}{\partial y}}\end{pmatrix}}}$

представляет собой ньютоновский поток, фактически он может быть выражен как:

${\displaystyle {\begin{pmatrix}\tau _{xx}&\tau _{xy}\\\tau _{yx}&\tau _{yy}\end{pmatrix}}={\begin{pmatrix}x&0\\0&-t\end{pmatrix}}\cdot {\begin{pmatrix}{\frac {\partial u}{\partial x}}&{\frac {\partial u}{\partial y}}\\{\frac {\partial v}{\partial x}}&{\frac {\partial v}{\partial y}}\end{pmatrix}}}$,

т.е. анизотропное течение с тензором вязкости:

${\displaystyle {\begin{pmatrix}\mu _{xx}&\mu _{xy}\\\mu _{yx}&\mu _{yy}\end{pmatrix}}={\begin{pmatrix}x&0\\0&-t\end{pmatrix}}}$

который является неоднородным (зависит от пространственных координат) и нестационарным, но, соответственно, не зависит от скорости потока:

${\displaystyle \mathbf {\mu } (x,t)={\begin{pmatrix}x&0\\0&-t\end{pmatrix}}}$

Следовательно, этот поток является ньютоновским. С другой стороны, поток, в котором вязкость была:

${\displaystyle {\begin{pmatrix}\mu _{xx}&\mu _{xy}\\\mu _{yx}&\mu _{yy}\end{pmatrix}}={\begin{pmatrix}{\frac {1}{u}}&0\\0&{\frac {1}{u}}\end{pmatrix}}}$

является неньютоновским, поскольку вязкость зависит от скорости потока. Этот неньютоновский поток изотропен (матрица пропорциональна единичной матрице), поэтому вязкость является просто скаляром:

${\displaystyle \mu (u)={\frac {1}{u}}}$

Измерение сенсорами

Датчик напряжения сдвига расходящейся кромки

Это соотношение можно использовать для измерения напряжения сдвига стенки. Если бы датчик мог напрямую измерять градиент профиля скорости у стенки, то умножение на динамическую вязкость дало бы напряжение сдвига. Такой датчик продемонстрировали А. А. Накви и В. К. Рейнольдс.^[6] Интерференционная картина, создаваемая при передаче луча света через две параллельные щели, образует сеть линейно расходящихся полос, которые, кажется, исходят из плоскости двух щелей (см. двухщелевой эксперимент ). Когда частица в жидкости проходит через полосы, приемник обнаруживает отражение полосы. Сигнал может быть обработан, и, зная угол полосы, высоту и скорость частицы можно экстраполировать. Измеренное значение градиента скорости стенки не зависит от свойств жидкости и, как результат, не требует калибровки. Последние достижения в технологии изготовления микрооптики позволили использовать интегрированный дифракционный оптический элемент для изготовления датчиков напряжения сдвига с расходящимися полосами, которые можно использовать как в воздухе и в жидкости.^[7]

Датчик напряжения сдвига на микростолбах

Еще один метод измерения заключается в использовании тонких настенных микростолб, изготовленных из гибкого полимерного ПДМС, которые изгибаются в ответ на приложение сил сопротивления в непосредственной близости от стены. Таким образом, датчик относится к принципам косвенного измерения, основанным на соотношении между градиентами скорости у стенки и локальным напряжением сдвига у стенки.^[8][9]

Смотрите также

• Критическое разрешенное напряжение сдвига
• Испытание на прямой сдвиг
• Диаграммы сдвига и момента
• Скорость сдвига
• Деформация сдвига
• Прочность на сдвиг
• Растягивающее напряжение
• Испытание на трехосный сдвиг

Рекомендации

1. Hibbeler, R.C. (2004). Механика материалов. Нью-Джерси США: Pearson Education. п. 32. ISBN  0-13-191345-X.
2. "Сопротивление материалов". Eformulae.com. Получено 24 декабря 2011.
3. Лекция Формула Журавского [Формула Журавского]. Сопромат Лекции (на русском). Получено 2014-02-26.
4. «Прогиб балок» (PDF). Лекции по машиностроению. Университет Макмастера.^{[постоянная мертвая ссылка ]}
5. День, Майкл А. (2004), Условие прилипания гидродинамики, Springer, Нидерланды, стр. 285–296, ISSN  0165-0106.
6. Naqwi, A. A .; Рейнольдс, В. К. (январь 1987 г.), "Двойной цилиндрический волновой лазерно-доплеровский метод измерения поверхностного трения в потоке жидкости", Технический отчет NASA STI / Recon N, 87
7. {Датчик напряжения сдвига microS, MSE}
8. Große, S .; Шредер, В. (2009), "Двумерная визуализация турбулентного сдвигового напряжения стенки с помощью микростолбиков", Журнал AIAA, 47 (2): 314–321, Bibcode:2009AIAAJ..47..314G, Дои:10.2514/1.36892
9. Große, S .; Шредер, В. (2008), «Измерение динамического напряжения сдвига стенки в турбулентном потоке в трубе с использованием датчика Micro-Pillar Sensor MPS.³", Международный журнал тепла и потока жидкости, 29 (3): 830–840, Дои:10.1016 / j.ijheatfluidflow.2008.01.008