Дебая модель - Debye model
| Статистическая механика |
|---|
 |
В термодинамика и физика твердого тела, то Дебая модель это метод, разработанный Питер Дебай в 1912 г. для оценки фонон вклад в удельная теплоемкость (теплоемкость) в твердый.[1] Он лечит вибрации из атомная решетка (тепло) как фононы в коробке, в отличие от Модель Эйнштейна, который рассматривает твердое тело как множество отдельных, не взаимодействующих квантовые гармонические осцилляторы. Модель Дебая правильно предсказывает низкотемпературную зависимость теплоемкости, которая пропорциональна - в Дебай Т3 закон. Как и Модель Эйнштейна, он также восстанавливает Закон Дюлонга – Пети при высоких температурах. Но из-за упрощающих предположений его точность страдает при промежуточных температурах.
Вывод
Модель Дебая представляет собой твердотельный эквивалент Закон планка излучения черного тела, где угощают электромагнитное излучение как фотонный газ. Модель Дебая рассматривает атомные колебания как фононы в коробке (коробка - сплошная). Большинство этапов расчета идентичны, поскольку оба являются примерами безмассового Бозе-газ с линейным дисперсионным соотношением.
Рассмотрим куб из стороны . От частица в коробке В статье резонирующие моды звуковых возмущений внутри ящика (учитывая пока только те, которые выровнены по одной оси) имеют длины волн, определяемые
куда целое число. Энергия фонона равна
куда является Постоянная Планка и - частота фонона. Делая приближение, что частота обратно пропорциональна длине волны, мы имеем:
в котором - скорость звука внутри твердого тела. В трех измерениях мы будем использовать:
в котором - величина трехмерного импульса фонона.
Приближение, согласно которому частота обратно пропорциональна длине волны (что дает постоянную скорость звука), подходит для фононов низкой энергии, но не для фононов высокой энергии (см. Статью о фононы.) Это несогласие является одним из ограничений модели Дебая и соответствует некорректности результатов при промежуточных температурах, тогда как как при низких, так и при высоких температурах они точны.
Теперь давайте посчитаем полную энергию в коробке,
куда число фононов в ящике с энергией . Другими словами, полная энергия равна сумме энергии, умноженной на количество фононов с этой энергией (в одном измерении). В трех измерениях у нас есть:
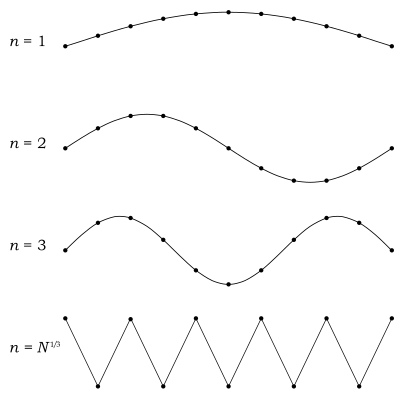
Здесь Дебая модель и Закон планка излучения черного тела отличаются. В отличие от электромагнитного излучения в ящике существует конечное количество фонон энергетические состояния, потому что фонон не может иметь произвольно высоких частот. Его частота ограничена средой его распространения - атомной решеткой твердого тела. Рассмотрим иллюстрацию поперечного фонона ниже.
Разумно предположить, что минимальная длина волны фонон вдвое больше расстояния между атомами, как показано на нижнем рисунке. Есть атомы в твердом теле. Наше твердое тело - это куб, а значит, есть атомов на край. Разделение атомов тогда дается выражением , а минимальная длина волны равна
сделать максимальное количество режима (бесконечно для фотоны )
Это число ограничивает верхний предел тройной энергетической суммы
Для медленно изменяющихся функций с хорошим поведением сумму можно заменить интегралом (также известным как Приближение Томаса – Ферми )
Пока не было упоминания о , количество фононов с энергией Фононы подчиняются Статистика Бозе – Эйнштейна. Их распределение дается известной формулой Бозе – Эйнштейна
Поскольку фонон имеет три возможных состояния поляризации (одно продольный, и два поперечный которые примерно не влияют на его энергию) формулу выше необходимо умножить на 3,
(На самом деле используется эффективная скорость звука , т.е. температура Дебая (см. ниже) пропорционально , точнее , где различают продольную и поперечную скорости звуковой волны (вклады 1/3 и 2/3 соответственно). Температура Дебая или эффективная скорость звука является мерой твердости кристалла.)
Подстановка в интеграл энергии дает
Легкость, с которой эти интегралы вычисляются для фотоны Это связано с тем, что частота света, по крайней мере, в полуклассическом понимании, не связана. Как показано на рисунке выше, это неверно для фононы. Чтобы аппроксимировать этот тройной интеграл, Дебай использованные сферические координаты
и аппроксимировали куб восьмой частью сферы
куда - радиус этой сферы, который определяется сохранением числа частиц в кубе и восьмой части сферы. Объем куба равен объемы элементарной ячейки,
итак получаем:
Замена правильного интеграла интегрированием по сфере вносит в модель еще один источник неточности.
Интеграл энергии принимает вид
Изменение переменной интегрирования на ,
Чтобы упростить внешний вид этого выражения, определите Температура Дебая
Где объем кубического бокса .
Много ссылок[2][3] описывают температуру Дебая просто как сокращение для некоторых констант и переменных, зависящих от материала. Однако, как показано ниже, примерно равна энергии фононов моды с минимальной длиной волны, и поэтому мы можем интерпретировать температуру Дебая как температуру, при которой возбуждается самая высокочастотная мода (и, следовательно, каждая мода).
Продолжая, у нас есть удельная внутренняя энергия:
куда это (третий) Функция Дебая.
Дифференцируя по получаем безразмерную теплоемкость:
Эти формулы относятся к модели Дебая при всех температурах. Более элементарные формулы, приведенные ниже, дают асимптотику в пределе низких и высоких температур. Как уже упоминалось, это поведение точное, в отличие от промежуточного поведения. Основная причина точности при низких и высоких энергиях, соответственно, заключается в том, что модель Дебая дает (i) точное соотношение дисперсии на низких частотах, а (ii) соответствует точному плотность состояний , относительно количества колебаний в частотном интервале.
Вывод Дебая
Дебай вывел свое уравнение несколько иначе и проще. С помощью механика сплошной среды, он обнаружил, что количество колебательных состояний с частотой меньше определенного значения асимптотично
в котором это объем и это фактор, который он рассчитал из коэффициенты эластичности и плотность. Комбинируя эту формулу с ожидаемой энергией гармонического осциллятора при температуре T (уже использованной Эйнштейн в его модели) дала бы энергию
если колебательные частоты продолжаются до бесконечности. Эта форма дает поведение, правильное при низких температурах. Но Дебай понял, что не может быть больше, чем колебательные состояния для N атомов. Он сделал предположение, что в атомном твердом теле спектр частот колебательных состояний будет продолжать следовать указанному выше правилу вплоть до максимальной частоты выбрано так, чтобы общее количество состояний :
Дебай знал, что это предположение было неверным (более высокие частоты расположены ближе, чем предполагалось), но оно гарантирует правильное поведение при высокой температуре ( Закон Дюлонга – Пети ). Тогда энергия определяется как:
- куда является .
куда функция, получившая название третьего порядка Функция Дебая.
Другой вывод
Сначала мы выводим распределение частот колебаний; следующий вывод основан на Приложении VI от.[4] Рассмотрим трехмерное изотропное упругое тело с N атомами в форме прямоугольного параллелепипеда с длинами сторон . Упругая волна будет подчиняться волновое уравнение и будет плоские волны; рассмотреть волновой вектор и определить . Обратите внимание, что у нас есть
(1)
Решения волновое уравнение находятся
и с граничные условия в , у нас есть
(2)
куда положительные целые числа. Подставив (2) в (1), а также используя соотношение дисперсии , у нас есть
Приведенное выше уравнение для фиксированной частоты , описывает восьмую часть эллипса в "пространстве мод" (восьмую, потому что положительные). Количество режимов с частотой менее есть, таким образом, число целых точек внутри эллипса, которое в пределе (т.е. для очень большого параллелепипеда) может быть аппроксимирован объемом эллипса. Следовательно, количество режимов с частотой в диапазоне является
(3)
куда - объем параллелепипеда. Обратите внимание на то, что скорость волны в продольном направлении отличается от поперечного направления и что волны могут быть поляризованы в одну сторону в продольном направлении и двумя способами в поперечном направлении; таким образом мы определяем .
После вывода из[5] определяем верхний предел частоты вибрации ; поскольку в твердом теле N атомов, имеется 3N квантовых гармонических осцилляторов (по 3 для каждого направления x, y, z), колеблющихся в диапазоне частот . Следовательно, мы можем определить вот так:
- .
(4)
Определив , где k Постоянная Больцмана и его Постоянная Планка, и подставив (4) в (3), мы получили
(5)
это определение более стандартное. Мы можем найти вклад энергии для всех осцилляторов, колеблющихся с частотой . Квантовые гармонические осцилляторы могут иметь энергии куда и используя Статистика Максвелла-Больцмана, количество частиц с энергией является
- .
Энергетический вклад осцилляторов с частотой затем
- .
(6)
Отмечая, что (потому что есть моды, колеблющиеся с частотой ), у нас есть
Сверху мы можем получить выражение для 1 / A; подставив его в (6), у нас есть
Интегрирование по ν дает
Предел низкой температуры
Температура дебаевского твердого тела называется низкой, если , что приводит к
Этот определенный интеграл можно вычислить точно:
В низкотемпературном пределе ограничения модели Дебая, упомянутые выше, не применяются, и она дает правильное соотношение между (фононной) теплоемкостью, температурой, коэффициентами упругости и объемом, приходящимся на атом (последние величины содержатся в Температура Дебая).
Предел высокой температуры
Температура дебаевского твердого тела называется высокой, если . С помощью если приводит к
Это Закон Дюлонга – Пети, и является довольно точным, хотя не учитывает ангармонизм, который вызывает дальнейшее увеличение теплоемкости. Полная теплоемкость твердого тела, если это дирижер или же полупроводник, также может содержать значительный вклад от электронов.
Дебай против Эйнштейна

Итак, насколько близко модели Дебая и Эйнштейна соответствуют эксперименту? Удивительно близко, но Дебай верен при низких температурах, а Эйнштейн - нет.
Насколько разные модели? Чтобы ответить на этот вопрос, естественно построить их на одном наборе осей ... за исключением одной. И модель Эйнштейна, и модель Дебая обеспечивают функциональная форма по теплоемкости. Они есть модели, и ни одна модель не обходится без масштаба. Масштаб соотносит модель с ее реальным аналогом. Видно, что масштаб модели Эйнштейна, который задается
является . А масштаб модели Дебая составляет , температура Дебая. И то и другое обычно находят путем подгонки моделей к экспериментальным данным. (Температуру Дебая теоретически можно рассчитать, исходя из скорости звука и размеров кристалла.) Поскольку эти два метода подходят к проблеме с разных направлений и разной геометрии, шкалы Эйнштейна и Дебая являются нет то же самое, то есть
это означает, что их построение на одном наборе осей не имеет смысла. Это две модели одного и того же, но разного масштаба. Если определить Температура Эйнштейна в качестве
тогда можно сказать
и, чтобы связать эти два, мы должны найти соотношение
В Эйнштейн твердый состоит из Один-частота квантовые гармонические осцилляторы, . Эта частота, если бы она действительно существовала, была бы связана со скоростью звука в твердом теле. Если представить распространение звука как последовательность атомов удары друг друга, тогда становится очевидным, что частота колебаний должна соответствовать минимальной длине волны, поддерживаемой атомной решеткой, .
что делает Температура Эйнштейна
и искомое соотношение, следовательно,
Теперь обе модели можно построить на одном графике. Обратите внимание, что это соотношение является кубическим корнем из отношения объема одного октанта трехмерной сферы к объему содержащего его куба, который является просто поправочным коэффициентом, используемым Дебаем при аппроксимации интеграла энергии выше.
С другой стороны, соотношение двух температур можно рассматривать как отношение одной частоты Эйнштейна, на которой колеблются все осцилляторы, и максимальной частоты Дебая. Тогда единственная частота Эйнштейна может рассматриваться как среднее значение частот, доступных для модели Дебая.
Таблица температур Дебая
Хотя модель Дебая не совсем верна, она дает хорошее приближение для низкотемпературной теплоемкости изолирующих кристаллических твердых тел, где другие вклады (например, высокомобильные электроны проводимости) пренебрежимо малы. Для металлов вклад электронов в тепло пропорционален , который при низких температурах доминирует над дебаевским результат для колебаний решетки. В этом случае можно сказать, что модель Дебая является приближенной только для решетки вклад к удельной теплоемкости. В следующей таблице приведены температуры Дебая для нескольких чистых элементов.[2] и сапфир:
|
|
|
|
Подгонка модели Дебая к экспериментальным данным часто феноменологически улучшается, позволяя температуре Дебая становиться зависимой от температуры;[6] например, значение для водяного льда увеличивается примерно с 222 K[7] до 300 К[8] как температура идет от абсолютный ноль примерно до 100 К.
Распространение на другие квазичастицы
Для других бозонный квазичастицы, например, для магноны (квантованные спиновые волны) в ферромагнетиках вместо фононы (квантованные звуковые волны) можно легко получить аналогичные результаты. В этом случае на низких частотах разные дисперсионные соотношения, например, в случае магнонов вместо для фононов (с ). У одного тоже разные плотность состояний (например., ). Как следствие, в ферромагнетиках появляется магнонный вклад в теплоемкость: , доминирующую при достаточно низких температурах фононный вклад, . В металлах же, напротив, основной низкотемпературный вклад в теплоемкость , исходит от электронов. это фермионный, и рассчитывается разными методами, начиная с Зоммерфельд с модель свободных электронов.
Распространение на жидкости
Долгое время считалось, что теория фононов не способна объяснить теплоемкость жидкостей, поскольку жидкости содержат только продольные, но не поперечные фононы, которые в твердых телах отвечают за 2/3 теплоемкости. Тем не мение, Рассеяние Бриллюэна эксперименты с нейтронами и с рентгеновскими лучами, подтверждая интуицию Яков Френкель,[9] показали, что поперечные фононы действительно существуют в жидкостях, хотя и ограничены частотами выше порога, называемого Частота Френкеля. Поскольку большая часть энергии содержится в этих высокочастотных модах, простой модификации модели Дебая достаточно, чтобы получить хорошее приближение к экспериментальной теплоемкости простых жидкостей.[10]
Частота Дебая
В Частота Дебая (Символ: или же ) - параметр модели Дебая. Это относится к отключению угловая частота за волны гармонической цепочки масс, используемой для описания движения ионы в кристаллическая решетка а точнее, чтобы правильно предсказать теплоемкость в таких кристаллах быть постоянными при высоких температурах (Закон Дюлонга – Пети ). Термин был впервые введен Питер Дебай в 1912 г.[11]
На протяжении всей статьи периодические граничные условия предполагаются.
Определение
Если предположить соотношение дисперсии является
- ,
с то скорость звука в кристалле; и k волнового вектора значение дебаевской частоты имеет следующий вид:
Для одномерной одноатомной цепочки частота Дебая равна[12]
- ,
с расстояние между двумя соседними атомами в цепочке, когда система находится в основное состояние (в данном случае это означает, что ни один из атомов не движется относительно друг друга); общее количество атомов в цепочке; и размер (объем) системы (длина цепочки); и это линейная числовая плотность. Где выполняется следующее соотношение: .
Для двумерной одноатомной квадратной решетки частота Дебая равна
- ,
куда и такие же, как и раньше; - размер (площадь) поверхности; и то поверхностная плотность числа.
Для трехмерного одноатомного примитивный кубический кристалл, частота Дебая равна[13]
- ,
куда и такие же, как и раньше; размер системы; и то объемная числовая плотность.
Скорость звука в кристалле может зависеть (среди прочего) от массы атомов, силы их взаимодействия, давление в системе и / или поляризация волны (продольной или поперечной), но в дальнейшем мы сначала будем предполагать, что скорость звука одинакова для любой поляризации (это предположение, однако, не имеет далеко идущих последствий).[14]
Предполагаемый соотношение дисперсии легко доказывается, что это неверно для одномерной цепочки масс, но в модели Дебая это не оказалось проблемой.
Отношение к температуре Дебая
Температура Дебая еще один параметр в модели Дебая, связан с частотой Дебая соотношением
куда сокращенный Постоянная Планка и это Постоянная Больцмана.
Вывод Дебая
Трехмерный кристалл
В выводе Дебая теплоемкость он суммирует все возможные режимы системы. То есть: включая разные направления и поляризации. Он предположил, что общее количество мод на поляризацию равно (с количество масс в системе), или математическим языком[14]
- ,
где с обеих сторон из-за трех поляризаций, поэтому сумма проходит по всем модам для одной конкретной поляризации. Дебай сделал это предположение, потому что знал от классическая механика что количество мод на поляризацию в цепочке масс всегда должно быть равно количеству масс в цепочке.
Левая часть теперь должна быть сделана явной, чтобы показать, как она зависит от частоты Дебая (здесь просто введена как частота среза, то есть: более высокие частоты, чем частота Дебая, не могут существовать), чтобы выражение для нее могло быть найденным.
Прежде всего, предполагая быть очень большим (>> 1, с размер системы в любом из трех направлений) наименьший волновой вектор в любом направлении можно аппроксимировать следующим образом: , с . Меньшие волновые векторы не могут существовать из-за периодические граничные условия. Таким образом, суммирование стало бы 4
- ,
куда ; размер системы; и интеграл (как суммирование) по всем возможным режимам, который считается конечной областью (ограниченной частотой среза).
Тройной интеграл можно было бы переписать как единый интеграл по всем возможным значениям модуля (видеть: Якобиан для сферических координат ). Результат
- ,
с модуль волнового вектора, соответствующий дебаевской частоте, поэтому .
Поскольку мы знаем, что дисперсионное соотношение , это можно записать в виде интеграла по всем возможным
- ,
После решения интеграла он снова приравнивается к найти
- .
Вывод:
- .
Одномерная цепочка в трехмерном пространстве
Такой же вывод можно сделать для одномерной цепочки атомов. Количество мод остается неизменным, поскольку поляризации по-прежнему три. Так
- .
Остальная часть вывода аналогична предыдущему, поэтому снова переписывается левая часть;
- .
На последнем этапе умножение на два происходит потому, что работает отрицательно, но не. Мы продолжим;
- .
Вывод:
- .
Двумерный кристалл
Такой же вывод можно было бы сделать для двумерного кристалла. Опять же, количество мод остается неизменным, потому что есть еще три поляризации. Вывод аналогичен двум предыдущим. Начнем с того же уравнения,
- .
А затем переписывается левая часть и приравнивается к
- ,
куда размер системы.
Вывод
- .
Позволяя поляризации иметь значение
Как упоминалось во введении: в общем, продольные волны имеют скорость волны, отличную от поперечных. Для ясности сначала предполагалось, что они равны, но теперь мы отказываемся от этого предположения.
Дисперсионное соотношение принимает вид , куда , которые соответствуют трем поляризациям. Частота среза (частота Дебая), однако, не зависит от . И мы можем записать общее количество режимов как , что снова равно . Здесь суммирование по модам (хотя и не указано явно) зависит от .
Одно измерение
Снова переписывается суммирование по модам.
- .
Результат
- .
Таким образом, частота Дебая находится
- .
Или предположив, что две поперечные поляризации одинаковы (имеют одинаковую фазовую скорость и частоту)
- .
Можно проверить, что это соотношение эквивалентно найденному ранее (когда поляризация не имела значения), установив .
Два измерения
Такой же вывод можно сделать для двумерного кристалла, чтобы найти (вывод аналогичен предыдущим выводам)
- .
Или предположив, что две поперечные поляризации равны (хотя для двух измерений было бы логичнее, если бы все поляризации были разными):
- .
Опять же, можно проверить, что это отношение эквивалентно найденному ранее, установив .
Три измерения
Такой же вывод можно сделать для трехмерного кристалла, чтобы найти (вывод аналогичен предыдущим выводам)
- .
Или предположив, что две поперечные поляризации равны (хотя для трех измерений было бы более логично, когда все поляризации были бы одинаковыми):
- .
Опять же, можно проверить, что это отношение эквивалентно найденному ранее, установив .
Вывод с фактическим соотношением дисперсии

Эту проблему можно было бы сделать более проницательной, сделав ее более сложной. Вместо использования дисперсионного соотношения , the correct dispersion relation is now going to be assumed. From classical mechanics it is known that for an equidistant chain of masses which interact harmonically with each other the dispersion relation reads as follows[14]
.
After plotting this relation, it is clear that Debye's estimation of the cut-off wavelength was right after all. Because for every wavenumber bigger than (that is: меньше чем ) a wavenumber that is smaller than could be found with the same angular frequency. This means the resulting physical manifestation for the mode with the larger wavenumber is indistinguishable from the one with the smaller wavenumber. Thereby, the study of the dispersion relation can be limited to the first brillouin zone[15] i.e. for .This is possible because the system consists of дискретизированный points, as is demonstrated in the animated picture. Dividing the dispersion relation by и вставка за , we find the speed of a wave with быть
.
By simply inserting in the original dispersion relation we find
.
Combining these results the same result is once again found
.
However, for diatomic chains (and more complex chains) the associated cut-off frequency (and wavelength) is not very accurate, since the cut-off wavelength is twice as big and the dispersion relation consists of two branches (for a diatomic chain). It is also not certain from this whether for more dimensional systems the cut-off frequency was accurately predicted by Debye.
Альтернативное происхождение

For a one dimensional chain this result could also be reproduced using theory on aliasing. В Теорема выборки Найквиста – Шеннона is used in the following derivation; the main difference being that in the following derivation the discretization is not in time, but in space. If we use the correct dispersion relation from last paragraph, it will be clear in another insightful way why the cut-off frequency has the value previously (twice) derived. So again,
предполагается.
This derivation is completely equivalent to the previous one, that is: the same assumptions are made to retrieve the result. It is not more or less accurate, it is just a different approach.
To determine where the cut-off frequency should be, it is useful to first determine where the cut-off of the wavelength should be. From the dispersion relation we know that for every mode is repeated, so the cut-off wavelength would be at . From this and the periodic boundary conditions you can immediately see that the total number of modes per polarization would be . As seen in the gif of the previous paragraph this is because every wave with a wavelength shorter than could be replaced by a wave with a wavelength longer than to regain the same physical result.
However, the dispersion relation from previous paragraph (the correct one) is not even necessary in reasoning as to why the cut-off should be at . Because, as is depicted, only waves with a longer wavelength than could render the same physical result as another one. So this is another way to correctly predict the cut-off wavelength without using the correct dispersion relation (or even knowledge from classical mechanics as Debye did). However, using the wrong dispersion relation which Debye assumed, waves with a smaller wavelength would have a higher frequency, but the relative movement of the masses would be the same, so this does not render new modes.
This results again in , rendering
.
Also here it does not matter which dispersion relation is used (the correct one or the one Debye used), the same cut-off frequency would be found.
Unfortunately, the same method could not be used (as easily) for a two- or three-dimensional crystal, because diagonal waves would have a larger cut-off wavelength, which are also difficult to predict.
Смотрите также
Рекомендации
- ^ Debye, Peter (1912). "Zur Theorie der spezifischen Waerme". Annalen der Physik (на немецком). 39 (4): 789–839. Bibcode:1912AnP...344..789D. Дои:10.1002/andp.19123441404.
- ^ а б Kittel, Charles (2004). Введение в физику твердого тела (8-е изд.). Джон Вили и сыновья. ISBN 978-0471415268.
- ^ Schroeder, Daniel V. "An Introduction to Thermal Physics" Addison-Wesley, San Francisco (2000). Section 7.5
- ^ Hill, Terrell L. (1960). An Introduction to Statistical Mechanics. Reading, Massachusetts, U.S.A.: Addison-Wesley Publishing Company, Inc. ISBN 9780486652429.
- ^ Oberai, M. M.; Srikantiah, G (1974). A First Course in Thermodynamics. New Delhi, India: Prentice-Hall of India Private Limited. ISBN 9780876920183.
- ^ Patterson, James D; Bailey, Bernard C. (2007). Solid-State Physics: Introduction to the Theory. Springer. С. 96–97. ISBN 978-3-540-34933-4.
- ^ Shulman, L. M. (2004). "The heat capacity of water ice in interstellar or interplanetary conditions". Астрономия и астрофизика. 416: 187–190. Bibcode:2004A&A...416..187S. Дои:10.1051/0004-6361:20031746.
- ^ Flubacher, P.; Leadbetter, A. J.; Morrison, J. A. (1960). "Heat Capacity of Ice at Low Temperatures". Журнал химической физики. 33 (6): 1751. Bibcode:1960JChPh..33.1751F. Дои:10.1063/1.1731497.
- ^ In his textbook Kinetic Theory of Liquids (engl. 1947)
- ^ Bolmativ, Brazhin, Trachenko, The phonon theory of liquid thermodynamics, Sci Rep 2:421 (2012)
- ^ Debye, P. (1912). "Zur Theorie der spezifischen Wärmen". Annalen der Physik. 344 (14): 789–839. Дои:10.1002/andp.19123441404. ISSN 1521-3889.
- ^ "The one dimensional monatomic solid" (PDF). Получено 2018-04-27.
- ^ Fitzpatrick, Richard (2006). "Specific heats of solids". Ричард Фицпатрик Техасский университет в Остине. Получено 2018-04-27.
- ^ а б c Simon, Steven H. (2013-06-20). The Oxford Solid State Basics (Первое изд.). Оксфорд: Издательство Оксфордского университета. ISBN 9780199680764. OCLC 859577633.
- ^ Srivastava, G. P. (2019-07-16). The Physics of Phonons. Рутледж. ISBN 978-1-351-40955-1.
дальнейшее чтение
- CRC Справочник по химии и физике, 56th Edition (1975–1976)
- Schroeder, Daniel V. Введение в теплофизику. Addison-Wesley, San Francisco (2000). Section 7.5.


















![{ sqrt [{3}] {N}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2632439311fdaac0db5c94be22a66bc4759c3b3e)
![L / { sqrt [{3}] {N}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68ce3128288fa487eb59b377703ca3c31b6ac01d)
![lambda _ { rm {min}} = {2L over { sqrt [{3}] {N}}} ,,](https://wikimedia.org/api/rest_v1/media/math/render/svg/67ce39568ba1619356396b79fafe20ab2a5b958f)
![n _ { rm {max}} = { sqrt [{3}] {N}} ,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/52e26b34255058c420ca488f519532157f051097)
![U = sum _ {n_ {x}} ^ { sqrt [{3}] {N}} sum _ {n_ {y}} ^ { sqrt [{3}] {N}} sum _ { n_ {z}} ^ { sqrt [{3}] {N}} E_ {n} , { bar {N}} (E_ {n}) ,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/fec6d96639ee52ea7d4e59bc75e719fe094fd5ce)
![U приблизительно int _ {0} ^ { sqrt [{3}] {N}} int _ {0} ^ { sqrt [{3}] {N}} int _ {0} ^ { sqrt [{3}] {N}} E (n) , { bar {N}} left (E (n) right) , dn_ {x} , dn_ {y} , dn_ {z } ,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f378b750c04cde69b47b010798779902e74825b)








![U = int _ {0} ^ { sqrt [{3}] {N}} int _ {0} ^ { sqrt [{3}] {N}} int _ {0} ^ { sqrt [{3}] {N}} E (n) , {3 over e ^ {E (n) / kT} -1} , dn_ {x} , dn_ {y} , dn_ {z} ,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b05660b876347cc0556fce9c94b050d78867006)




![R = { sqrt [{3}] {6N over pi}} ,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f9d4e2bc889e4df97cb5eb25a732323e6d7dbd1)



![{ displaystyle T _ { rm {D}} { stackrel { mathrm {def}} {=}} {hc _ { rm {s}} R over 2Lk} = {hc _ { rm {s} } over 2Lk} { sqrt [{3}] {6N over pi}} = {hc _ { rm {s}} over 2k} { sqrt [{3}] {{6 over pi } {N over V}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b2de73de320ca49f94520eaf2e41ad8da780a24)


































![[0, ню]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3da4e6ef6d591bf2a9654be4fb845ce59a91551)




![[0, nu _ {D}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9a2adfa6354fb9930ff419a40f847263676830c)































![{ displaystyle nu = {c _ { rm {s}} over lambda} = {c _ { rm {s}} { sqrt [{3}] {N}} over 2L} = {c_ { rm {s}} over 2} { sqrt [{3}] {N over V}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81e4239b96057ece4c87c6d1b2436c71a0f892a5)
![{ displaystyle T _ { rm {E}} = { epsilon over k} = {h nu over k} = {hc _ { rm {s}} over 2k} { sqrt [{3}] {N over V}} ,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e04158867129c173bc190d9c60e4d6422c382ed)
![{ displaystyle {T _ { rm {E}} over T _ { rm {D}}} = { sqrt [{3}] { pi over 6}} = 0.805995977 ...}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb2c9648e406d584fff25220a7a9593260228d6d)
































































![{ displaystyle k in [- { frac { pi} {a}}, { frac { pi} {a}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d53bd66da593951b382a4535c648edcd83de9890)







