Большой канонический ансамбль - Grand canonical ensemble
| Статистическая механика |
|---|
 |
В статистическая механика, а большой канонический ансамбль (также известный как макроканонический ансамбль) статистический ансамбль который используется для представления возможных состояний механической системы частиц, находящихся в термодинамическое равновесие (термический и химический) с резервуаром.[1] Система называется открытой в том смысле, что система может обмениваться энергией и частицами с резервуаром, так что различные возможные состояния системы могут различаться как по их полной энергии, так и по общему количеству частиц. Объем, форма и другие внешние координаты системы остаются неизменными во всех возможных состояниях системы.
Термодинамические переменные большого канонического ансамбля: химический потенциал (символ: µ) и абсолютная температура (символ: Т). Ансамбль также зависит от механических переменных, таких как объем (символ: V), которые влияют на характер внутренних состояний системы. Поэтому этот ансамбль иногда называют мкВт ансамбль, поскольку каждая из этих трех величин является константой ансамбля.
Основы
Проще говоря, большой канонический ансамбль задает вероятность п каждому отдельному микросостояние задается следующей экспонентой:
куда N - количество частиц в микросостоянии и E - полная энергия микросостояния. k является Постоянная Больцмана.
Номер Ω известен как большой потенциал и постоянна для ансамбля. Однако вероятности и Ω будет отличаться, если отличается µ, V, Т выбраны. Великий потенциал Ω выполняет две роли: обеспечивает коэффициент нормализации для распределения вероятностей (вероятности по полному набору микросостояний должны в сумме равняться единице); и многие важные средние по ансамблю могут быть непосредственно вычислены с помощью функции Ω (µ, V, Т).
В случае, когда разрешено изменять количество частиц более одного вида, вероятностное выражение обобщается на
куда µ1 - химический потенциал для частиц первого типа, N1 - количество таких частиц в микросостоянии, µ2 - химический потенциал для частиц второго сорта и т. д. (s - количество различных видов частиц). Однако эти числа частиц следует определять осторожно (см. примечание о сохранении числа частиц ниже).
Большие ансамбли подходят для использования при описании таких систем, как электроны в дирижер, или фотоны в полости, форма которой фиксирована, но энергия и количество частиц могут легко колебаться из-за контакта с резервуаром (например, с заземлением или темная поверхность, в этих случаях). Большой канонический ансамбль обеспечивает естественную среду для точного вывода Статистика Ферми – Дирака или же Статистика Бозе – Эйнштейна для системы невзаимодействующих квантовых частиц (см. примеры ниже).
- Примечание по рецептуре
- В альтернативной формулировке той же концепции вероятность записывается как , с использованием большая функция раздела а не грандиозный потенциал. Уравнения в этой статье (в терминах большого потенциала) могут быть переформулированы в терминах большой статистической суммы с помощью простых математических манипуляций.
Применимость
Большой канонический ансамбль - это ансамбль, который описывает возможные состояния изолированной системы, находящейся в тепловом и химическом равновесии с резервуаром (вывод происходит по аналогии с выводом термостата нормальной канонический ансамбль, и его можно найти в Reif[2]). Большой канонический ансамбль применим к системам любого размера, маленького или большого; необходимо только предположить, что резервуар, с которым он контактирует, намного больше (т. е. принять макроскопический предел ).
Условие изолированности системы необходимо для того, чтобы гарантировать, что у нее есть четко определенные термодинамические величины и эволюция.[1] На практике, однако, желательно применять большой канонический ансамбль для описания систем, которые находятся в прямом контакте с резервуаром, поскольку именно этот контакт обеспечивает равновесие. Использование большого канонического ансамбля в этих случаях обычно оправдывается либо 1) предположением, что контакт является слабым, либо 2) включением части соединения резервуара в анализируемую систему, так что влияние соединения на область правильно смоделирован интерес. В качестве альтернативы можно использовать теоретические подходы для моделирования влияния связи, что дает открытый статистический ансамбль.
Другой случай, когда возникает большой канонический ансамбль, - это рассмотрение большой и термодинамической системы (системы, находящейся «в равновесии с самой собой»). Даже если точные условия системы на самом деле не допускают вариаций энергии или числа частиц, большой канонический ансамбль можно использовать для упрощения расчетов некоторых термодинамических свойств. Причина в том, что различные термодинамические ансамбли (микроканонический, канонический ) становятся в некоторых аспектах эквивалентными большому каноническому ансамблю, когда система становится очень большой.[примечание 1] Конечно, для небольших систем разные ансамбли больше не эквивалентны даже в среднем. В результате большой канонический ансамбль может быть очень неточным при применении к небольшим системам с фиксированным числом частиц, таким как атомные ядра.[3]
Характеристики
- Уникальность: Большой канонический ансамбль однозначно определяется для данной системы при данной температуре и данных химических потенциалах и не зависит от произвольных выборов, таких как выбор системы координат (классическая механика) или базиса (квантовая механика).[1]
- Статистическое равновесие (устойчивое состояние): великий канонический ансамбль не развивается с течением времени, несмотря на то, что основная система находится в постоянном движении. В самом деле, ансамбль является только функцией сохраняющихся количеств системы (энергии и числа частиц).[1]
- Тепловое и химическое равновесие с другими системами: Две системы, каждая из которых описывается великим каноническим ансамблем равных температур и химических потенциалов, приведенных в тепловой и химический контакт.[заметка 2] останется неизменным, и полученная комбинированная система будет описываться большим каноническим ансамблем тех же температур и химических потенциалов.[1]
- Максимальная энтропия: Для заданных механических параметров (фиксировано V), среднее по большому каноническому ансамблю логарифмической вероятности - <журнал п> (также называемая «энтропией») является максимально возможным для любого ансамбля (т. е. распределение вероятностей п) с тем же <E>, <N1>, так далее.[1]
- Минимальный грандиозный потенциал: Для заданных механических параметров (фиксировано V) и заданные значения Т, µ1, …, µs, среднее по ансамблю <E + kT бревно п − µ1N1 − … µsNs> это самый низкий из возможных ансамблей.[1]
Большой потенциал, средние по ансамблю и точные дифференциалы
Частные производные функции Ω (µ1, …, µs, V, Т) дать важные средние величины большого канонического ансамбля:[1][4]
- средние числа частиц
- среднее давление
- то Энтропия Гиббса
- и средняя энергия
Точный дифференциал: Из приведенных выше выражений видно, что функция Ω имеет точный дифференциал
Первый закон термодинамики: Подставляя указанное выше отношение на ⟨E⟩ в точный дифференциал Ω, уравнение, подобное первый закон термодинамики найдено, за исключением средних знаков некоторых величин:[1]
Термодинамические колебания: The отклонения по энергии и числу частиц[5][6]
Корреляции в колебаниях: The ковариации числа частиц и энергии[1]
Примеры ансамблей
Полезность большого канонического ансамбля иллюстрируется приведенными ниже примерами. В каждом случае великий потенциал рассчитывается на основе соотношения
что требуется для суммирования вероятностей микросостояний до 1.
Статистика невзаимодействующих частиц
Бозоны и фермионы (квантовые)
В частном случае квантовой системы многих невзаимодействующий частиц, термодинамику просто вычислить.[7]Поскольку частицы не взаимодействуют, можно вычислить серию одночастичных стационарные состояния, каждая из которых представляет собой отделимую часть, которая может быть включена в общее квантовое состояние системы. А пока будем называть эти одночастичные стационарные состояния как орбитали (чтобы не путать эти «состояния» с общим состоянием многих тел), при условии, что каждое возможное свойство внутренней частицы (вращение или же поляризация ) считается отдельной орбиталью. Каждая орбиталь может быть занята частицей (или частицами) или может быть пустой.
Поскольку частицы не взаимодействуют, мы можем придерживаться точки зрения, что каждая орбиталь образует отдельную термодинамическую системуТаким образом, каждая орбиталь сама по себе представляет собой грандиозный канонический ансамбль, настолько простой, что его статистика может быть немедленно выведена здесь. Сосредоточение внимания только на одной орбитальной метке я, полная энергия для микросостояние из N частицы на этой орбитали будут Nϵя, куда ϵя является характерным уровнем энергии этой орбитали. Большой потенциал орбитали задается одной из двух форм, в зависимости от того, является ли орбиталь бозонной или фермионной:
- За фермионы, то Принцип исключения Паули допускает только два микросостояния для орбитали (заполнение 0 или 1), давая двухчленный ряд
- За бозоны, N может быть любым неотрицательным целым числом, и каждое значение N считается одним микросостоянием из-за неразличимость частиц, ведущий к геометрическая серия:
В каждом случае значение дает термодинамическое среднее число частиц на орбитали: Распределение Ферми – Дирака для фермионов, а Распределение Бозе – Эйнштейна для бозонов. Рассматривая снова всю систему, общий великий потенциал находится путем сложения Ωя для всех орбиталей.
Неразличимые классические частицы
В классической механике также можно рассматривать неразличимые частицы (фактически, неразличимость является предпосылкой для последовательного определения химического потенциала; все частицы данного вида должны быть взаимозаменяемыми.[1]). Мы снова рассматриваем возможность помещения нескольких частиц одного вида в одно и то же микросостояние одночастичного фазового пространства, которое мы снова называем «орбитальным». Однако по сравнению с квантовой механикой классический случай усложняется тем фактом, что микросостояние в классической механике относится не к одной точке в фазовом пространстве, а к расширенной области в фазовом пространстве: одно микросостояние содержит бесконечное количество состояний, все разные, но похожего характера. В результате, когда несколько частиц помещаются на одну и ту же орбиталь, общий набор частиц (в системном фазовом пространстве) не считается одним целым микросостоянием, а скорее всего дробная часть микросостояния, потому что идентичные состояния (образованные перестановкой одинаковых частиц) не должны быть пересчитаны. Поправочный коэффициент перерасчета - это факториал количества частиц.
Статистика в этом случае принимает форму экспоненциального степенного ряда
Значение соответствующий Статистика Максвелла – Больцмана.
Ионизация изолированного атома
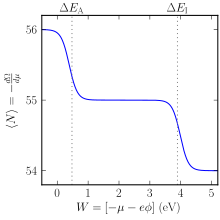
Большой канонический ансамбль может использоваться, чтобы предсказать, предпочитает ли атом находиться в нейтральном состоянии или в ионизированном состоянии. Атом может существовать в ионизированном состоянии с большим или меньшим количеством электронов по сравнению с нейтральным. Как показано ниже, ионизированные состояния могут быть термодинамически предпочтительными в зависимости от окружающей среды. Рассмотрим упрощенную модель, в которой атом может находиться в нейтральном состоянии или в одном из двух ионизированных состояний (подробный расчет также включает факторы вырождения состояний[8]):
- нейтральное состояние, с N0 электроны и энергия E0.
- ан окисленный государственный (N0 − 1 электронов) с энергией E0 + ΔEя + qϕ
- а уменьшенный государственный (N0 + 1 электронов) с энергией E0 - ΔEА − qϕ
Здесь ΔEя и ΔEА атомы энергия ионизации и электронное сродство, соответственно; ϕ местный электростатический потенциал в вакууме рядом с атомом, и −q это заряд электрона.
Таким образом, великий потенциал в этом случае определяется
Количество −qϕ − µ в данном случае имеет решающее значение для определения баланса между различными состояниями. Это значение определяется окружающей средой вокруг атома.
Если один из этих атомов поместить в вакуумный ящик, то −qϕ − µ = W, то рабочая функция материала футеровки коробки. Сравнение таблиц рабочая функция для различных твердых материалов с таблицами электронное сродство и энергия ионизации для атомных разновидностей ясно, что многие комбинации приведут к нейтральному атому, однако некоторые конкретные комбинации могут привести к тому, что атом предпочтет ионизированное состояние: например, галоген атом в иттербий коробка, или цезий атом в вольфрам коробка. При комнатной температуре эта ситуация нестабильна, поскольку атом стремится к адсорбировать к открытой подкладке коробки вместо того, чтобы свободно плавать. Однако при высоких температурах атомы испаряются с поверхности в ионной форме; это спонтанное поверхностная ионизация эффект был использован как цезий ионный источник.[9]
При комнатной температуре этот пример находит применение в полупроводники, где ионизация присадка атом хорошо описывается этим ансамблем.[8] В полупроводнике зона проводимости край ϵC играет роль уровня энергии вакуума (заменяя −qϕ), и µ известен как Уровень Ферми. Конечно, энергия ионизации и сродство к электрону атома примеси сильно изменяются по сравнению с их вакуумными значениями. Типичная донорная легирующая примесь в кремнии, фосфор, имеет ΔEя = 45 мэВ;[10]значение ϵC − µ в собственном кремнии изначально около 600 мэВ, гарантируя ионизацию легирующей примеси. ϵC − µ Однако сильно зависит от электростатики, поэтому при некоторых обстоятельствах можно деионизировать легирующую добавку.
Значение химического потенциала, обобщенное «число частиц»
Чтобы число частиц имело связанный химический потенциал, оно должно сохраняться во время внутренней динамики системы и может изменяться только тогда, когда система обменивается частицами с внешним резервуаром.
Если частицы могут быть созданы из энергии во время динамики системы, то связанный мкН член не должен появляться в вероятностном выражении для большого канонического ансамбля. По сути, это то же самое, что требовать µ = 0 для такой частицы. Так обстоит дело с фотоны в черной полости, число которых регулярно меняется из-за поглощения и излучения на стенках полости. (С другой стороны, фотоны в резонаторе с высокой отражающей способностью могут сохраняться и иметь ненулевое значение µ.[11])
В некоторых случаях количество частиц не сохраняется и N представляет собой более абстрактную сохраняемую величину:
- Химические реакции: Химические реакции могут преобразовывать один тип молекул в другой; если возникают реакции, то Nя должны быть определены таким образом, чтобы они не изменялись во время химической реакции.
- Физика частиц высоких энергий: Обычные частицы могут рождаться из чистой энергии, если античастица создано. Если такой процесс разрешен, то не сохраняется ни количество частиц, ни количество античастиц. Вместо, N = (число частиц - число античастиц) сохраняется.[12][заметка 3] По мере увеличения энергии частиц появляется больше возможностей для преобразования между типами частиц, и поэтому количество действительно сохраняемых чисел уменьшается. При самых высоких энергиях сохраняются только числа. электрический заряд, слабый изоспин, и барионное число - лептонное число.
С другой стороны, в некоторых случаях частицы одного вида могут иметь несколько сохраняющихся номеров:
- Закрытые отсеки: В системе, состоящей из нескольких отсеков, которые разделяют энергию, но не разделяют частицы, можно установить химические потенциалы отдельно для каждого отсека. Например, конденсатор состоит из двух изолированных проводов и заряжается за счет разницы в электронный химический потенциал.
- Медленное уравновешивание: В некоторых квазиравновесных ситуациях возможно иметь две различные популяции частиц одного и того же типа в одном и том же месте, каждая из которых уравновешена внутренне, но не друг с другом. Хотя это и не совсем равновесие, может быть полезно назвать квазиравновесные химические потенциалы, которые могут различаться в разных популяциях. Примеры: (физика полупроводников ) отчетливый квазиуровни Ферми (электронно-химические потенциалы) в зона проводимости и валентная полоса; (спинтроника ) различные химические потенциалы вращения вверх и вниз; (криогеника ) отчетливый параводород и ортоводород химические потенциалы.
Точные выражения для ансамбля
Точное математическое выражение для статистических ансамблей имеет различную форму в зависимости от типа рассматриваемой механики (квантовой или классической), поскольку понятие «микросостояние» значительно отличается. В квантовой механике большой канонический ансамбль дает простое описание, поскольку диагонализация дает набор различных микросостояния системы, каждая с четко определенной энергией и числом частиц. Классический механический случай более сложен, поскольку он включает не стационарные состояния, а интеграл по каноническим фазовое пространство.
Квантовая механика
Статистический ансамбль в квантовой механике представлен матрица плотности, обозначаемый . Большой канонический ансамбль - это матрица плотности[нужна цитата ]
куда ЧАС - оператор полной энергии системы (Гамильтониан ), N̂1 это общая оператор числа частиц для частиц типа 1, N̂2 это общая оператор числа частиц для частиц типа 2 и т. д. exp это матричная экспонента оператор. Великий потенциал Ω определяется условием нормировки вероятности того, что матрица плотности имеет след одного, :
Отметим, что для большого ансамбля базисные состояния операторов ЧАС, N̂1и т. д. все состояния с несколько частиц в Пространство фока, и матрица плотности определяется на той же основе. Поскольку энергия и число частиц сохраняются по отдельности, эти операторы коммутируют друг с другом.
В качестве альтернативы большой канонический ансамбль можно записать в простой форме, используя обозначение бюстгальтера, так как можно (учитывая взаимно коммутирующий характер операторов энергии и числа частиц) найти полную основа одновременных собственных состояний |ψя⟩, проиндексировано я, куда ЧАС|ψя⟩ = Eя|ψя⟩, N̂1|ψя⟩ = N1,я|ψя⟩, и так далее. Учитывая такой собственный базис, великий канонический ансамбль просто
где сумма берется по полному набору состояний с состоянием я имея Eя общая энергия, N1,я частицы типа 1, N2,я частицы типа 2 и т. д.
Классическая механика
В классической механике большой ансамбль представлен совместная функция плотности вероятности определяется по нескольким фазовые пространства различных размеров, ρ(N1, … Ns, п1, … пп, q1, … qп), где п1, … пп и q1, … qп являются канонические координаты (обобщенные импульсы и обобщенные координаты) внутренних степеней свободы системы. Выражение большого канонического ансамбля несколько тоньше, чем канонический ансамбль поскольку:[1]
- Количество частиц и, следовательно, количество координат п варьируется между различными фазовыми пространствами, и,
- жизненно важно учитывать, считается ли перестановка подобных частиц отдельным состоянием или нет.
В системе частиц число степеней свободы п зависит от количества частиц в зависимости от физической ситуации. Например, в трехмерном газе моноатомов п = 3Nоднако в молекулярных газах также будут вращательные и колебательные степени свободы.
Функция плотности вероятности для большого канонического ансамбля:
куда
- E - энергия системы, функция фазы (N1, … Ns, п1, … пп, q1, … qп),
- час - произвольная, но заранее определенная константа с единицами измерения энергия × время, устанавливая размер одного микросостояния и обеспечивая правильные размеры для ρ.[примечание 4]
- C - поправочный коэффициент для перерасчета (см. ниже), функция N1, … Ns.
Опять же, значение Ω определяется требованием, чтобы ρ - нормированная функция плотности вероятности:
Этот интеграл берется по всей доступной фазовое пространство для заданного числа частиц.
Поправка на завышение
Хорошо известная проблема статистической механики жидкостей (газов, жидкостей, плазмы) состоит в том, как обращаться с частицами, похожими или идентичными по природе: следует ли их рассматривать как различимые или нет? В уравнении движения системы каждая частица всегда отслеживается как различимая сущность, и, тем не менее, существуют также допустимые состояния системы, в которых положения каждой частицы просто поменялись местами: эти состояния представлены в разных местах фазового пространства, но при этом будут кажутся эквивалентными.
Если рассматривать перестановки подобных частиц как отдельные состояния, то множитель C выше просто C = 1. С этой точки зрения ансамбли включают каждое переставленное состояние как отдельное микросостояние. Хотя сначала это кажется безобидным, это приводит к проблеме крайне неэкстенсивной энтропии в каноническом ансамбле, известной сегодня как Парадокс гиббса. В большом каноническом ансамбле возникает еще одна логическая несогласованность: количество различимых перестановок зависит не только от количества частиц в системе, но также от того, сколько частиц находится в резервуаре (поскольку система может обмениваться частицами с резервуаром). В этом случае энтропия и химический потенциал не являются экстенсивными, но также плохо определены, в зависимости от параметра (размера резервуара), который не должен иметь значения.
Для решения этих проблем необходимо, чтобы обмен двумя подобными частицами (внутри системы или между системой и резервуаром) не рассматривался как придающий различное состояние системы.[1][примечание 5] Чтобы учесть этот факт, интегралы по-прежнему переносятся на все фазовое пространство, но результат делится на
которое представляет собой количество различных возможных перестановок. Деление на C аккуратно исправляет перерасчет, который происходит в интеграле по всему фазовому пространству.
Конечно, можно включить различимые типы частиц в большом каноническом ансамбле - каждый различимый тип отслеживается отдельным счетчиком частиц и химический потенциал . В результате единственный последовательный способ включить «полностью различимые» частицы в большой канонический ансамбль - это рассмотреть все возможные различимые типы этих частиц и отслеживать каждый возможный тип с помощью отдельного счетчика частиц и отдельного химического потенциала.
Примечания
- ^ Цитируя Рейфа: «Для целей расчета средних значений физических величин не имеет значения, является ли макроскопическая система изолированной или находится в контакте с резервуаром, с которым она может только обмениваться энергией, или в контакте с резервуаром, с которым она может обмениваться как энергией, так и частицами. [...] В некоторых задачах, где ограничение фиксированного числа частиц является громоздким, можно, таким образом, легко обойти сложность, аппроксимируя реальную ситуацию с [...] большим каноническим распределением. "
- ^ Термический и химический контакт означает, что системы могут обмениваться энергией и частицами через соединение. Соединение должно быть слабым, чтобы не нарушать микросостояния системы.
- ^ Конечно, для значительной тепловой генерации пар частица-античастица требуются очень высокие температуры, например, порядка 109 K для создания электрон-позитронов, поэтому этот процесс не является предметом повседневной термодинамики.
- ^ (Историческая справка) Оригинальный ансамбль Гиббса эффективно установил час = 1 [единица энергии] × [единица времени], что приводит к зависимости от единицы значений некоторых термодинамических величин, таких как энтропия и химический потенциал. С появлением квантовой механики час часто принимается равным Постоянная Планка чтобы получить полуклассическое соответствие с квантовой механикой.
- ^ Это можно сравнить с канонический ансамбль где необязательно рассматривать частицы как различимые; это только дает N-зависимая ошибка энтропии, которая ненаблюдаема, пока N остается постоянным. В общем, однако, такой свободы нет: «когда число частиц в системе следует рассматривать как переменное, средний индекс вероятности для фаз, в общем случае определенных, соответствует энтропии». (Гиббс).
Рекомендации
- ^ а б c d е ж грамм час я j k л м Гиббс, Джозия Уиллард (1902). Элементарные принципы статистической механики. Нью-Йорк: Сыновья Чарльза Скрибнера.
- ^ Рейф Ф. (1965). Основы статистической и теплофизики. Макгроу-Хилл. ISBN 9780070518001.
- ^ Chaudhuri, G .; Гупта, С. (2007). «Удельная теплоемкость и бимодальность в канонической и большой канонической версиях термодинамической модели». Физический обзор C. 76 (1): 014619. arXiv:0704.0288. Bibcode:2007PhRvC..76a4619C. Дои:10.1103 / PhysRevC.76.014619.
- ^ http://www.theory.physics.manchester.ac.uk/~judith/stat_therm/node87.html
- ^ «Архивная копия» (PDF). Архивировано из оригинал (PDF) в 2013-10-19. Получено 2013-05-02.CS1 maint: заархивированная копия как заголовок (связь)
- ^ http://micro.stanford.edu/~caiwei/me334/Chap9_NPT_Grand_Canonical_Ensemble_v04.pdf
- ^ Srivastava, R.K .; Ашок, Дж. (2005). Статистическая механика. Нью-Дели: PHI Learning Pvt. ООО ISBN 9788120327825.
- ^ а б Балкански, М .; Уоллис, Р.Ф. (2000). Физика полупроводников и приложения. Издательство Оксфордского университета. ISBN 0198517408.
- ^ Альтон, Г. Д. (1988). «Характеристики источника ионизации поверхности цезия с пористым ионизатором вольфрама. I». Обзор научных инструментов. 59 (7): 1039–1044. Bibcode:1988RScI ... 59.1039A. Дои:10.1063/1.1139776.
- ^ http://www.iue.tuwien.ac.at/phd/wittmann/node7.html
- ^ Чути, К. (2014). «Статистические мерцания в конденсате Бозе-Эйнштейна фотонов». Физика. 7: 7. Bibcode:2014PhyOJ ... 7 .... 7C. Дои:10.1103 / Физика.7.7.
- ^ Бураковский, Л .; Horwitz, L.P .; Schieve, W. C. (1996). «Новая релятивистская высокотемпературная бозе-эйнштейновская конденсация». Физический обзор D. 54 (6): 4029–4038. arXiv:hep-th / 9604039. Bibcode:1996ПхРвД..54.4029Б. Дои:10.1103 / PhysRevD.54.4029. PMID 10021081.

































