Графики на SO (3) - Charts on SO(3)
В математика, то специальная ортогональная группа в трех измерениях, иначе известных как группа вращения SO (3), является естественным примером многообразие. Различные графики на SO (3) подставить соперника системы координат: в этом случае нельзя сказать, что существует предпочтительный набор параметры описывающий вращение. Есть три степени свободы, так что размерность SO (3) равна трем. Во многих приложениях используется та или иная система координат, и возникает вопрос, как перейти из одной системы в другую.
Пространство вращений
В геометрия то группа ротации это группа из всех вращения о происхождении трехмерного Евклидово пространство р3 под действием сочинение.[1] По определению, поворот вокруг начала координат - это линейное преобразование что сохраняет длина из векторов (это изометрия ) и сохраняет ориентация (т.е. руки) пространства. Сохраняющее длину преобразование, которое меняет ориентацию, называется преобразованием. неправильное вращение. Каждый неправильный поворот трехмерного евклидова пространства - это поворот, за которым следует отражение в плоскости через начало координат.
Составление двух вращений приводит к другому вращению; каждое вращение имеет уникальное обратное вращение; и карта идентичности удовлетворяет определению вращения. Благодаря указанным выше свойствам набор всех вращений является группа под состав. Более того, группа вращений имеет естественный многообразие структура, для которой групповые операции гладкий; так что это на самом деле Группа Ли. Группа вращения часто обозначается SO (3) по причинам, объясненным ниже.
Пространство вращений изоморфно множеству операторы вращения и набор ортонормированных матриц с определителем +1. Это также тесно связано (двойное покрытие ) с набором кватернионов с их внутренним произведением, а также с набором векторов вращения (хотя здесь отношение сложнее описать, подробнее см. ниже), с другой внутренней операцией композиции, заданной произведением их эквивалентных матриц .
Обозначения векторов вращения возникают из Теорема Эйлера вращения в котором говорится, что любое вращение в трех измерениях может быть описано поворотом на некоторый угол вокруг некоторой оси. Учитывая это, мы можем затем указать ось одного из этих вращений на два угла, и мы можем использовать радиус вектора, чтобы указать угол поворота. Эти векторы представляют собой мяч в 3D с необычной топологией.
Эта трехмерная твердая сфера эквивалентна поверхности четырехмерной сферы, которая также является трехмерной разновидностью. Для выполнения этой эквивалентности нам нужно будет определить, как мы будем представлять вращение с помощью этой четырехмерной встроенной поверхности.
Гиперсфера вращений
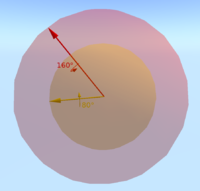
Визуализация гиперсферы
Интересно рассматривать пространство как трехмерную сферу. S3, граница диска в 4-мерном евклидовом пространстве. Для этого нам нужно будет определить, как мы представляем вращение с помощью этой внедренной в 4D поверхности.
Способ, которым можно использовать радиус для задания угла поворота, непрост. Это может быть связано с кругами широты в сфере с определенным северным полюсом и объясняется следующим образом:
Начиная с северного полюса сферы в трехмерном пространстве, мы указываем точку на северном полюсе для представления вращения идентичности. В случае единичного вращения ось вращения не определена, и угол поворота (ноль) не имеет значения. Вращение, ось которого содержится в ху-плоскость и очень маленький угол поворота могут быть заданы срезом сферы, параллельной плоскости ху-самолет и совсем рядом с северным полюсом. Круг, определяемый этим срезом, будет очень маленьким, что соответствует небольшому углу поворота. По мере того, как углы поворота становятся больше, срез перемещается на юг, а круги становятся больше, пока не будет достигнут экватор сферы, что будет соответствовать углу поворота 180 градусов. При продвижении на юг радиусы кругов становятся меньше (что соответствует абсолютному значению угла поворота, рассматриваемого как отрицательное число). Наконец, когда достигается южный полюс, круги снова сжимаются до вращения идентичности, которое также указывается как точка на южном полюсе. Обратите внимание, что с помощью этой визуализации можно увидеть ряд характеристик таких поворотов и их представлений.
Пространство поворотов непрерывно, каждое вращение имеет окрестность вращений, которые почти одинаковы, и эта окрестность становится плоской по мере уменьшения окрестности.
Псевдонимы

Кроме того, каждый поворот фактически представлен двумя противоположными точками на сфере, которые находятся на противоположных концах линии, проходящей через центр сферы. Это отражает тот факт, что каждое вращение может быть представлено как вращение вокруг некоторой оси или, что то же самое, как отрицательное вращение вокруг оси, указывающей в противоположном направлении (так называемый двойная крышка ). «Широта» круга, представляющего определенный угол поворота, будет составлять половину угла, представленного этим вращением, поскольку при перемещении точки с северного полюса на южный, широта изменяется от нуля до 180 градусов, а угол поворота колеблется от 0 до 360 градусов. («долгота» точки тогда представляет конкретную ось вращения.) Обратите внимание, однако, что этот набор вращений не замыкается при композиции.
Два последовательных поворота с осями в ху-плоскость не обязательно будет давать вращение, ось которого лежит в ху-плоскость, и поэтому не может быть представлена как точка на сфере. Этого не будет с обычным вращением в 3-м пространстве, которое действительно образует замкнутое множество при композиции.
Эта визуализация может быть расширена до обычного вращения в трехмерном пространстве. Тождественное вращение - это точка, а небольшой угол поворота вокруг некоторой оси можно представить как точку на сфере с малым радиусом. По мере увеличения угла поворота сфера увеличивается, пока угол поворота не достигнет 180 градусов, после чего сфера начинает сжиматься, становясь точкой, когда угол приближается к 360 градусам (или нулю градусов от отрицательного направления). Этот набор расширяющихся и сжимающихся сфер представляет собой гиперсфера в четырехмерном пространстве (3-сфера).
Как и в более простом примере выше, каждому вращению, представленному в виде точки на гиперсфере, соответствует его противоположная точка на этой гиперсфере. «Широта» на гиперсфере будет составлять половину соответствующего угла поворота, и окрестность любой точки станет «более плоской» (т.е. будет представлена трехмерным евклидовым пространством точек) по мере того, как окрестность сжимается.
Этому поведению соответствует набор единичных кватернионов: общий кватернион представляет точку в четырехмерном пространстве, но ограничение его единичной величины дает трехмерное пространство, эквивалентное поверхности гиперсферы. Величина единичного кватерниона будет равна единице, что соответствует гиперсфере единичного радиуса.
Векторная часть единичного кватерниона представляет радиус 2-сферы, соответствующей оси вращения, а ее величина является синусом половины угла вращения. Каждое вращение представлено двумя единичными кватернионами противоположного знака, и, как и в пространстве вращений в трех измерениях, кватернионный продукт двух единичных кватернионов даст единичный кватернион. Кроме того, пространство единичных кватернионов является «плоским» в любой бесконечно малой окрестности данного единичного кватерниона.
Параметризации
Мы можем параметризовать пространство вращений несколькими способами, но вырождения будут появляться всегда. Например, если мы используем три угла (Углы Эйлера ) такая параметризация вырождена в некоторых точках гиперсферы, что приводит к проблеме карданный замок. Этого можно избежать, используя четыре евклидовых координаты ш,Икс,у,z, с ш2 + Икс2 + у2 + z2 = 1. Точка (ш,Икс,у,z) представляет собой поворот вокруг оси, направленной вектором (Икс,у,z) под углом
Эта проблема аналогична параметризации двумерной поверхности сфера с двумя координатами, такими как широта и долгота. Широта и долгота плохо себя ведут (выродиться ) на северном и южном полюсах, хотя полюса по существу не отличаются от любых других точек на сфере. На полюсах (широты + 90 ° и −90 °) долгота теряет смысл. Можно показать, что никакая двухпараметрическая система координат не может избежать такого вырождения.
Возможные кандидаты параметризации включают:
- Углы Эйлера (θ, φ, ψ), представляющая произведение поворотов вокруг Икс, у и z топоры;
- Углы Тейта – Брайана (θ, φ, ψ), представляющая произведение поворотов вокруг Икс, у и z топоры;
- Угол оси пара (п, θ) единичного вектора, представляющего ось, и угол поворота вокруг нее;
- А кватернион q длины 1 (ср. Versor, кватернионы и пространственное вращение, 3-сфера ), компоненты которого также называют Параметры Эйлера – Родригеса;
- 3 × 3 кососимметричная матрица, через возведение в степень; кососимметричные матрицы 3 × 3 являются Алгебра Ли SO (3), и это экспоненциальное отображение в теории Ли;
- Рациональные параметры Кэли, основанные на Преобразование Кэли, пригодный для всех характеристик;
- Преобразования Мебиуса, действуя на Сфера Римана.
Проблемы параметризации
Существуют проблемы с их использованием как нечто большее, чем локальные диаграммы, из-за их многозначной природы и особенностей. То есть, прежде всего нужно быть осторожным, чтобы работать только с диффеоморфизмы в определении Диаграмма. Проблемы такого рода неизбежны, поскольку SO (3) диффеоморфен реальное проективное пространство п3(р), который является частным от S3 путем выявления противоположных точек, а диаграммы пытаются смоделировать многообразие, используя р3.
Это объясняет, почему, например, углы Эйлера дают переменную в 3-тор, а единичные кватернионы в 3-сфера. Единственность представления углами Эйлера в некоторых точках нарушается (ср. карданный замок ), в то время как представление кватерниона всегда двойная крышка, с q и -q давая такое же вращение.
Если мы используем кососимметричную матрицу, каждая кососимметричная матрица 3 × 3 определяется тремя параметрами, и поэтому на первый взгляд пространство параметров р3. Возведение в степень такая матрица приводит к ортогональной матрице 3 × 3 с определителем 1 - другими словами, матрице вращения, но это отображение «многие к одному». Обратите внимание, что это не карта покрытия - хотя это локальный гомеоморфизм вблизи начала координат, это не покрывающая карта при поворотах на 180 градусов. Эти матрицы можно ограничить шаром вокруг начала координат в р3 чтобы повороты не превышали 180 градусов, и это будет взаимно однозначно, за исключением поворотов на 180 градусов, которые соответствуют границе S2, и они определяют противоположные точки - это вырезать место. 3-шар с таким обозначением границы равен п3(р). Аналогичная ситуация имеет место для применения преобразования Кэли к кососимметричной матрице.
Угол оси дает параметры в S2 × S1; если мы заменим единичный вектор фактической осью вращения, так что п и -п дают ту же осевую линию, набор осей становится п2(р), реальная проективная плоскость. Но поскольку вращение вокруг п и -п параметризуются противоположными значениями θ, в результате S1 связать п2(р), который оказывается п3(р).
Дробно-линейные преобразования используют четыре комплексных параметра, а, б, c, и d, с условием, что объявление−до н.э не равно нулю. Поскольку умножение всех четырех параметров на одно и то же комплексное число не меняет параметр, мы можем настаивать на том, что объявление−до н.э= 1. Это предполагает написание (а,б,c,d) как комплексную матрицу 2 × 2 с определителем 1, то есть как элемент специальной линейной группы SL (2,C). Но не все такие матрицы производят вращения: конформные отображения на S2 также включены. Чтобы получить только вращения, мы настаиваем на том, чтобы d является комплексным сопряжением а, и c отрицательное значение комплексно сопряженного б. Тогда у нас есть два комплексных числа, а и б, при условии |а|2+|б|2= 1. Если мы напишем а+Ъ, это кватернион единичной длины.
В конечном итоге, поскольку р3 не является п3(р), с каждым из этих подходов будет проблема. В некоторых случаях нам нужно помнить, что определенные значения параметров приводят к одинаковому вращению, и для устранения этой проблемы необходимо установить границы, но затем путь через эту область в р3 затем должен внезапно перейти в другую область, когда пересекает границу. Блокировка кардана представляет собой проблему, когда производная карты не имеет полного ранга, что происходит с углами Эйлера и углами Тейта – Брайана, но не для других вариантов. Представление кватерниона не имеет ни одной из этих проблем (поскольку везде отображается отображение два к одному), но оно имеет 4 параметра с условием (единичная длина), что иногда затрудняет просмотр трех доступных степеней свободы.
Приложения
Одна из областей, в которой эти соображения в той или иной форме становятся неизбежными, - это кинематика из жесткое тело. Можно принять за определение идею изгиб в Евклидова группа E(3) трехмерного Евклидово пространство, начиная с тождества (исходной позиции). Подгруппа переводов Т из E(3) является нормальная подгруппа, с фактором SO (3), если мы рассмотрим подгруппу E+(3) из прямые изометрии только (что разумно в кинематике). Поступательная часть может быть отделена от вращательной части в стандартной ньютоновской кинематике, учитывая движение центра масс и вращения твердого тела вокруг центра масс. Следовательно, любое движение твердого тела приводит непосредственно к SO (3), если исключить поступательную часть.
Эти отождествления показывают, что SO (3) связаны но нет односвязный. Что касается последнего, то в шаре с выделенными точками противоположной поверхности рассмотрим путь, идущий от «северного полюса» прямо через центр к южному полюсу. Это замкнутая петля, поскольку идентифицируются северный полюс и южный полюс. Этот цикл не может быть сокращен до точки, поскольку независимо от того, как вы деформируете цикл, начальная и конечная точки должны оставаться противоположными, иначе цикл «разомкнется». С точки зрения вращений, этот цикл представляет собой непрерывную последовательность вращений вокруг z- ось, начинающаяся и заканчивающаяся при единичном повороте (т.е. серия поворотов на угол φ, где φ проходит от 0 до 2π).
Удивительно, но если вы пройдете путь дважды, то есть от северного полюса вниз к южному полюсу и обратно к северному полюсу, так что φ будет изменяться от 0 до 4π, вы получите замкнутый контур, который может быть сжатым до одной точки: сначала непрерывно перемещайте пути к поверхности шара, по-прежнему дважды соединяя северный полюс с южным. Затем вторую половину пути можно отразить на противоположной стороне, вообще не меняя путь. Теперь у нас есть обычная замкнутая петля на поверхности шара, соединяющая северный полюс с самим собой по большому кругу. Этот круг без проблем можно сжать до северного полюса. В Трюк с балийской тарелкой и подобные приемы демонстрируют это практически.
Тот же аргумент можно использовать в целом, и он показывает, что фундаментальная группа SO (3) является циклическая группа порядка 2. В физических приложениях нетривиальность фундаментальной группы допускает существование объектов, известных как спиноры, и является важным инструментом в развитии спин-статистическая теорема.
В универсальный чехол SO (3) является Группа Ли называется Отжим (3). Группа Spin (3) изоморфна группе особая унитарная группа СУ (2); он также диффеоморфен единице 3-сфера S3 и может пониматься как группа кватернионы единиц (т.е. те, у кого абсолютная величина 1). Связь между кватернионами и вращениями, обычно используемая в компьютерная графика, объясняется в кватернионы и пространственные вращения. Карта из S3 на SO (3), который идентифицирует противоположные точки S3 это сюръективный гомоморфизм групп Ли, с ядро {± 1}. Топологически это отображение взаимно однозначно. карта покрытия.
Смотрите также
Рекомендации
- ^ Якобсон (2009), стр. 34, Исх. 14.


