Карданный замок - Gimbal lock

Самолет заблокирован на подвесе. Когда стабилизаторы тангажа (зеленый) и рыскания (пурпурный) выровнены, они меняются на крен (синий) и рысканье применяют такое же вращение к самолету.

Добавление четвертой оси вращения может решить проблему блокировки кардана, но для этого требуется, чтобы самое внешнее кольцо активно приводилось в движение, чтобы оно оставалось на 90 градусов не совмещенным с самой внутренней осью (валом маховика). Без активного приведения в движение самого дальнего кольца все четыре оси могут выровняться в плоскости, как показано выше, что снова приводит к блокировке кардана и невозможности качения.

Карданный замок потеря одного степень свободы в трехмерном, трехмерномподвес механизм, который возникает, когда оси двух из трех карданов приводятся в параллельную конфигурацию, "запирая" систему в вращение в вырожденном двумерном пространстве.

Слово замок вводит в заблуждение: подвес не фиксируется. Все три подвеса могут по-прежнему свободно вращаться вокруг соответствующих осей подвески. Тем не менее, из-за параллельной ориентации двух осей подвеса нет подвеса, который мог бы обеспечить вращение вокруг одной оси.

Карданы

Основная статья: Подвес

Подвес - это подвесное кольцо, которое может вращаться вокруг оси. Подвесы обычно вложены друг в друга, чтобы обеспечить вращение вокруг нескольких осей.

Они появляются в гироскопы И в инерциальные единицы измерения чтобы внутренний стабилизатор оставался неизменной, в то время как внешняя подвеска кардана принимает любую ориентацию. В компасы и маховик накопителя энергии механизмы они позволяют объектам оставаться в вертикальном положении. Они используются для ориентации двигатели на ракетах.^[1]

Немного системы координат в математике ведут себя так, как если бы для измерения углов использовались настоящие карданы, в частности Углы Эйлера.

В случае трех или менее гнездовых подвесов блокировка подвеса неизбежно происходит в какой-то момент системы из-за свойств перекрытия (описано ниже).

В машиностроении

Хотя только две конкретные ориентации обеспечивают точную фиксацию кардана, практические механические карданы сталкиваются с трудностями вблизи этих ориентаций. Когда набор подвесов близок к заблокированной конфигурации, небольшие повороты платформы подвеса требуют больших движений окружающих подвесов. Хотя передаточное число бесконечно только в точке блокировки кардана, практические ограничения скорости и ускорения карданов - из-за инерции (возникающей из-за массы каждого кольца кардана), трения подшипника, сопротивления потоку воздуха или другой жидкости, окружающей карданный вал. подвесы (если они не находятся в вакууме) и другие физические и инженерные факторы - ограничивают движение платформы вблизи этой точки.

В двух измерениях

Блокировка кардана может происходить в карданных системах с двумя степенями свободы, такими как теодолит с вращениями вокруг азимут и возвышение в двух измерениях. Эти системы могут блокировать подвес при зенит и надир потому что в этих точках азимут четко не определен, и вращение в азимутальном направлении не меняет направления, на которое указывает теодолит.

Рассмотрите возможность отслеживания вертолета, летящего к теодолиту с горизонта. Теодолит представляет собой телескоп, установленный на штативе, чтобы он мог перемещаться по азимуту и ​​углу места для отслеживания вертолета. Вертолет летит к теодолиту и отслеживается телескопом по углу места и азимута. Вертолет летит непосредственно над треногой (т. Е. В зените), когда он меняет направление и летит под углом 90 градусов к своему предыдущему курсу. Телескоп не может отследить этот маневр без прерывистого скачка в одном или обоих положениях подвеса. Нет непрерывного движения, которое позволяет ему следовать за целью. Он находится в карданном замке. Таким образом, существует бесконечное количество направлений вокруг зенита, для которых телескоп не может непрерывно отслеживать все движения цели.^[2] Учтите, что даже если вертолет не проходит зенит, а только возле зенит, так что блокировка кардана не происходит, система все равно должна двигаться исключительно быстро, чтобы отслеживать его, поскольку он быстро переходит от одного подшипника к другому. Чем ближе к зениту находится ближайшая точка, тем быстрее это должно быть сделано, и если она действительно проходит через зенит, предел этих «все более быстрых» движений становится бесконечно быстрый, а именно прерывистый.

Чтобы выйти из блокировки подвеса, пользователь должен обойти зенит - явно: уменьшить высоту, изменить азимут, чтобы он соответствовал азимуту цели, а затем изменить высоту, чтобы соответствовать цели.

Математически это соответствует тому, что сферические координаты не определяют карта координат на сфере в зените и надире. В качестве альтернативы соответствующая карта Т²→S² от тор Т² в сферу S² (задается точкой с заданными азимутом и углом места) не является карта покрытия в этих точках.

В трех измерениях

Подвес с 3-мя осями вращения. Набор из трех подвесов, установленных вместе, чтобы обеспечить три степени свободы: крен, тангаж и рыскание. Когда два кардана вращаются вокруг одной оси, система теряет одну степень свободы.

Нормальная ситуация: три подвеса независимы

Блокировка кардана: два из трех карданов находятся в одной плоскости, теряется одна степень свободы

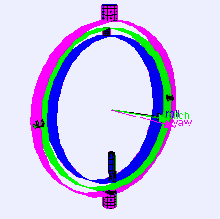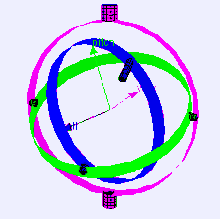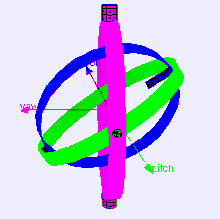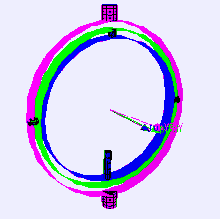
Рассмотрим случай платформы измерения уровня на самолете, летящем строго на север, с его тремя осями кардана, взаимно перпендикулярными (т. Е. рулон, подача и рыскание углы каждый ноль). Если самолет наклоняется на 90 градусов, кардан оси рыскания самолета и платформы становится параллельным кардану оси крена, и изменения вокруг рыскания больше не могут быть компенсированы.

Решения

Эта проблема может быть преодолена за счет использования четвертого кардана, активно приводимого в действие двигателем, чтобы поддерживать большой угол между осями кардана крена и рыскания. Другое решение - повернуть один или несколько подвесов в произвольное положение при обнаружении блокировки подвеса и, таким образом, перезагрузить устройство.

Современная практика заключается в полном отказе от использования подвесов. В контексте инерциальные навигационные системы, это можно сделать, установив инерциальные датчики непосредственно на кузов автомобиля (это называется страпон система)^[3] и цифровая интеграция измеренных значений вращения и ускорения с использованием кватернион методы определения ориентации и скорости транспортного средства. Другой способ замены кардана - использование жидкостных подшипников или флотационной камеры.^[4]

На Аполлоне 11

Известный инцидент с блокировкой карданного подвеса произошел в Аполлон-11 Миссия на Луну. На этом космическом корабле комплект карданов использовался на инерциальная единица измерения (ИДУ). Инженеры знали о проблеме с блокировкой кардана, но отказались от использования четвертого кардана.^[5] Некоторые причины этого решения очевидны из следующей цитаты:

«Похоже, что преимущества дублированного стабилизатора перевешиваются простотой оборудования, преимуществами в размере и соответствующей подразумеваемой надежностью блока с тремя степенями свободы прямого действия».

— Дэвид Хоаг, Журнал Apollo Lunar Surface Journal

Они предпочли альтернативное решение с использованием индикатора, который срабатывал бы при угле наклона около 85 градусов.

«Рядом с этой точкой в ​​замкнутом контуре стабилизации теоретически можно было бы дать команду моментным двигателям мгновенно повернуть стабилизатор на 180 градусов. Вместо этого в LM, компьютер высветил предупреждение о блокировке кардана при 70 градусах и заморозил IMU при 85 градусах "

— Пол Фьельд, Журнал Apollo Lunar Surface Journal

Вместо того, чтобы пытаться управлять подвесами быстрее, чем они могли, система просто отказалась и заморозила платформу. С этого момента космический аппарат нужно будет вручную отвести от положения фиксации карданного подвеса, а платформу придется вручную перенастроить, используя звезды в качестве ориентира.^[6]

После приземления лунного модуля Майк Коллинз на борту командного модуля шутил: "Как насчет того, чтобы послать мне четвертый стабилизатор на Рождество?"

Робототехника

Промышленный робот на литейном производстве.

В робототехнике блокировку карданного подвеса обычно называют «переворот запястья» из-за использования «запястья с тремя поворотами» в роботизированное оружие, где три оси запястья, управляющие рысканием, тангажем и креном, проходят через общую точку.

Пример переворота запястья, также называемого сингулярностью запястья, - это когда путь, по которому движется робот, выстраивает первую и третью оси запястья робота. Затем вторая ось запястья пытается повернуться на 180 ° за нулевое время, чтобы сохранить ориентацию рабочего органа. Результат сингулярности может быть весьма драматичным и отрицательно сказаться на манипуляторе робота, конечном эффекторе и процессе.

Важность предотвращения сингулярностей в робототехнике привела к тому, что в Американском национальном стандарте для промышленных роботов и робототехнических систем - Требования безопасности это определено как «состояние, вызванное коллинеарным выравниванием двух или более осей робота, приводящее к непредсказуемым движениям и скоростям роботов».^[7]

В прикладной математике

Проблема блокировки кардана возникает при использовании Углы Эйлера в прикладной математике; разработчики 3D компьютерные программы, Такие как 3D моделирование, встроенные навигационные системы, и видеоигры необходимо позаботиться о том, чтобы этого избежать.

На формальном языке блокировка кардана происходит потому, что отображение углов Эйлера на вращения (топологически, из 3-тора Т³ к реальное проективное пространство RP³ который совпадает с пространством трехмерных вращений SO3) не является локальный гомеоморфизм в каждой точке, и, следовательно, в некоторых точках классифицировать (степени свободы) должны быть ниже 3, при этом происходит блокировка кардана. Углы Эйлера позволяют дать численное описание любого вращение в трехмерном пространстве с использованием трех чисел, но это описание не только не уникально, но и есть некоторые точки, в которых не каждое изменение в целевом пространстве (повороты) может быть реализовано путем изменения исходного пространства (углов Эйлера). Это топологическое ограничение - не существует покрывающего отображения 3-тора в 3-мерное реальное проективное пространство; единственная (нетривиальная) накрывающая карта берется из 3-сферы, как при использовании кватернионы.

Для сравнения все переводы можно описать тремя числами ${\displaystyle x}$, ${\displaystyle y}$, и ${\displaystyle z}$, как последовательность трех последовательных линейных перемещений по трем перпендикулярным осям ${\displaystyle X}$, ${\displaystyle Y}$ и ${\displaystyle Z}$ топоры. То же самое и с вращениями: все повороты можно описать тремя числами. ${\displaystyle \alpha }$, ${\displaystyle \beta }$, и ${\displaystyle \gamma }$, как последовательность трех вращательных движений вокруг трех осей, перпендикулярных друг другу. Это сходство между линейными координатами и угловыми координатами делает углы Эйлера очень интуитивно понятный, но, к сожалению, они страдают от проблемы с блокировкой кардана.

Потеря степени свободы с углами Эйлера

Вращение в трехмерном пространстве можно представить численно с помощью матрицы несколькими способами. Одно из этих представлений:

${\displaystyle {\begin{aligned}R&={\begin{bmatrix}1&0&0\\0&\cos \alpha &-\sin \alpha \\0&\sin \alpha &\cos \alpha \end{bmatrix}}{\begin{bmatrix}\cos \beta &0&\sin \beta \\0&1&0\\-\sin \beta &0&\cos \beta \end{bmatrix}}{\begin{bmatrix}\cos \gamma &-\sin \gamma &0\\\sin \gamma &\cos \gamma &0\\0&0&1\end{bmatrix}}\end{aligned}}}$

Стоит рассмотреть пример, когда ${\displaystyle \beta ={\tfrac {\pi }{2}}}$. Знаю это ${\displaystyle \cos {\tfrac {\pi }{2}}=0}$ и ${\displaystyle \sin {\tfrac {\pi }{2}}=1}$, приведенное выше выражение становится равным:

${\displaystyle {\begin{aligned}R&={\begin{bmatrix}1&0&0\\0&\cos \alpha &-\sin \alpha \\0&\sin \alpha &\cos \alpha \end{bmatrix}}{\begin{bmatrix}0&0&1\\0&1&0\\-1&0&0\end{bmatrix}}{\begin{bmatrix}\cos \gamma &-\sin \gamma &0\\\sin \gamma &\cos \gamma &0\\0&0&1\end{bmatrix}}\end{aligned}}}$

Проведение матричное умножение:

${\displaystyle {\begin{aligned}R&={\begin{bmatrix}0&0&1\\\sin \alpha &\cos \alpha &0\\-\cos \alpha &\sin \alpha &0\end{bmatrix}}{\begin{bmatrix}\cos \gamma &-\sin \gamma &0\\\sin \gamma &\cos \gamma &0\\0&0&1\end{bmatrix}}&={\begin{bmatrix}0&0&1\\\sin \alpha \cos \gamma +\cos \alpha \sin \gamma &-\sin \alpha \sin \gamma +\cos \alpha \cos \gamma &0\\-\cos \alpha \cos \gamma +\sin \alpha \sin \gamma &\cos \alpha \sin \gamma +\sin \alpha \cos \gamma &0\end{bmatrix}}\end{aligned}}}$

И, наконец, используя формулы тригонометрии:

${\displaystyle {\begin{aligned}R&={\begin{bmatrix}0&0&1\\\sin(\alpha +\gamma )&\cos(\alpha +\gamma )&0\\-\cos(\alpha +\gamma )&\sin(\alpha +\gamma )&0\end{bmatrix}}\end{aligned}}}$

Изменение значений ${\displaystyle \alpha }$ и ${\displaystyle \gamma }$ в приведенной выше матрице имеет тот же эффект: угол поворота ${\displaystyle \alpha +\gamma }$ изменяется, но ось вращения остается в ${\displaystyle Z}$ направление: последний столбец и первая строка в матрице не изменятся. Единственное решение для ${\displaystyle \alpha }$ и ${\displaystyle \gamma }$ восстановить разные роли - значит изменить ${\displaystyle \beta }$.

Можно представить самолет, повернутый на упомянутые выше углы Эйлера, используя X-Y-Z соглашение. В этом случае первый угол - ${\displaystyle \alpha }$ это поле. Затем устанавливается значение Yaw. ${\displaystyle {\tfrac {\pi }{2}}}$ и заключительный поворот - по ${\displaystyle \gamma }$ - снова шаг самолета. Из-за блокировки кардана он потерял одну из степеней свободы - в данном случае способность катиться.

Также можно выбрать другое соглашение для представления поворота матрицей с использованием углов Эйлера, чем X-Y-Z соглашение выше, а также выбрать другие интервалы изменения для углов, но в конце всегда есть по крайней мере одно значение, для которого теряется степень свободы.

Проблема блокировки кардана не делает углы Эйлера «недействительными» (они всегда служат четко определенной системой координат), но делает их непригодными для некоторых практических приложений.

Альтернативное представление ориентации

Причина блокировки кардана представляет собой ориентацию в виде трех осевых вращений с Углы Эйлера. Поэтому потенциальное решение состоит в том, чтобы представить ориентацию каким-либо другим способом. Это могло быть как матрица вращения, кватернион (см. кватернионы и пространственное вращение ) или аналогичное представление ориентации, в котором ориентация рассматривается как значение, а не три отдельных связанных значения. Учитывая такое представление, пользователь сохраняет ориентацию как значение. Чтобы применить угловые изменения, ориентация изменяется с помощью дельта-угла / поворота оси. Полученную ориентацию необходимо повторно нормализовать, чтобы предотвратить ошибка с плавающей точкой от последовательных преобразований от накопления. Для матриц повторная нормализация результата требует преобразования матрицы в ее ближайшее ортонормированное представление. Для кватернионов повторная нормализация требует выполнение нормализации кватернионов.

Смотрите также

• Графики на SO (3)
• Динамика полета
• Сетка север (эквивалентная задача навигации в полярных экспедициях)
• Инерциальная навигационная система
• Планирование движения
• Кватернионы и пространственное вращение

Рекомендации

1. Джонатан Стрикленд (2008). «Что такое подвес и какое отношение он имеет к НАСА?».
2. Адриан Попа (4 июня 1998 г.). "Re: Что подразумевается под термином" карданный замок "?".
3. Крис Верплетсе (1995). «Обзор дизайна пера и фона навигации». Архивировано из оригинал 14 февраля 2009 г.
4. Чаппелл, Чарльз, Д. (2006). «Колодки опорные шарнирные газовые».
5. Дэвид Хоаг (1963). «Навигация и навигация Apollo - Соображения относительно фиксатора карданного подвеса Apollo IMU - Документ приборной лаборатории Массачусетского технологического института E-1344».
6. Эрик М. Джонс; Пол Фьельд (2006). "Углы подвеса, фиксатор кардана и четвертый подвес на Рождество".
7. ANSI / RIA R15.06-1999

внешняя ссылка

• Блокировка подвеса - объяснение в YouTube
• Блокировка подвеса за 30 секунд в YouTube