Диагональный аргумент Кантора - Cantors diagonal argument

Эта статья посвящена концепции множеств и теории чисел. Не следует путать с диагонализацией матрицы. Видеть диагонализация (значения) для нескольких других применений этого термина в математике.

Иллюстрация диагонального аргумента Кантора (в основании 2) для существования бесчисленные наборы. Последовательность внизу не может встречаться в перечисленных выше последовательностях.

An бесконечный набор может иметь то же самое мощность как должное подмножество самого себя, как изображено биекция ж(Икс)=2Икс от естественный к четные числа демонстрирует. Тем не менее существует бесконечное множество различных мощностей, как Диагональный аргумент Кантора показывает.

В теория множеств, Диагональный аргумент Кантора, также называемый аргумент диагонализации, то аргумент диагональной косой черты, то антидиагональный аргумент, или диагональный метод, был опубликован в 1891 г. Георг Кантор как математическое доказательство что есть бесконечные множества что не может быть помещено в индивидуальная переписка с бесконечным набором натуральные числа.^{[1][2]:20–[3]} Такие наборы теперь известны как бесчисленные наборы, а размер бесконечных множеств теперь рассматривается с помощью теории Количественные числительные который начал Кантор.

Диагональный аргумент не принадлежал Кантору первое доказательство несчетности действительные числа, появившийся в 1874 году.^[4][5]Однако он демонстрирует общую технику, которая с тех пор использовалась в широком спектре доказательств.^[6] в том числе первый из Теоремы Гёделя о неполноте^[2] и ответ Тьюринга на Entscheidungsproblem. Аргументы в пользу диагонализации часто также являются источником противоречий, таких как Парадокс Рассела^[7][8] и Парадокс ричарда.^[2]:27

Бесчисленное множество

В своей статье 1891 года Кантор рассмотрел набор Т всего бесконечного последовательности из двоичные цифры (т.е. каждая цифра равна нулю или единице). Он начинается с конструктивное доказательство следующей теоремы:

Если s₁, s₂, … , s_п,… - любое перечисление элементов из Т, то всегда есть элемент s из Т что соответствует нет s_п в перечислении.

Доказательство начинается с перечисления элементов из Т, Например:

s1 =	(0,	0,	0,	0,	0,	0,	0,	...)
s2 =	(1,	1,	1,	1,	1,	1,	1,	...)
s3 =	(0,	1,	0,	1,	0,	1,	0,	...)
s4 =	(1,	0,	1,	0,	1,	0,	1,	...)
s5 =	(1,	1,	0,	1,	0,	1,	1,	...)
s6 =	(0,	0,	1,	1,	0,	1,	1,	...)
s7 =	(1,	0,	0,	0,	1,	0,	0,	...)
...

Далее последовательность s строится выбором 1-й цифры как дополнительный до 1-й цифры s₁ (замена 0s для 1s и наоборот), 2-я цифра дополняет 2-ю цифру s₂, 3-я цифра как дополнительная к 3-й цифре s₃, и вообще для каждого п, то п^th цифра как дополнение к п^th цифра s_п. В приведенном выше примере это дает:

s1	=	(0,	0,	0,	0,	0,	0,	0,	...)
s2	=	(1,	1,	1,	1,	1,	1,	1,	...)
s3	=	(0,	1,	0,	1,	0,	1,	0,	...)
s4	=	(1,	0,	1,	0,	1,	0,	1,	...)
s5	=	(1,	1,	0,	1,	0,	1,	1,	...)
s6	=	(0,	0,	1,	1,	0,	1,	1,	...)
s7	=	(1,	0,	0,	0,	1,	0,	0,	...)
...
s	=	(1,	0,	1,	1,	1,	0,	1,	...)

По конструкции, s отличается от каждого s_п, поскольку их п^th цифры различаются (выделено в примере). Следовательно, s не может встречаться в перечислении.

Основываясь на этой теореме, Кантор затем использует доказательство от противного чтобы показать, что:

Набор Т бесчисленное множество.

Доказательство начинается с предположения, что Т является счетный.Тогда все его элементы можно записать в виде перечисления s₁, s₂, ... , s_п, .... Применение предыдущей теоремы к этому перечислению дает последовательность s не входящие в перечисление. Однако это противоречит s являясь элементом Т и, следовательно, принадлежат перечислению. Это противоречие означает, что исходное предположение неверно. Следовательно, Т бесчисленное множество.

Действительные числа

Бесчисленность действительные числа уже был установлен Первое доказательство несчетности Кантора, но это также следует из приведенного выше результата. Чтобы доказать это, инъекция будет построена из множества Т бесконечных двоичных строк в набор р реальных чисел. С Т неисчислимо, изображение этой функции, которая является подмножеством р, несчетное количество. Следовательно, р бесчисленное множество. Также, используя метод построения, разработанный Кантором, биекция будет построен между Т и р. Следовательно, Т и р имеют одинаковую мощность, которая называется "мощность континуума "и обычно обозначается ${\displaystyle {\mathfrak {c}}}$ или же ${\displaystyle 2^{\aleph _{0}}}$.

Укол от Т к р дается отображением строк в Т в десятичные дроби, например отображение т = 0111 ... с точностью до 0,0111 .... Эта функция, определяемая ж (т) = 0.т, это инъекция, потому что она отображает разные строки на разные числа.

Построение биекции между Т и р немного сложнее: вместо преобразования 0111 ... в десятичную дробь 0,0111 ... она может быть преобразована в основание б число: 0,0111 ..._б. Это приводит к семейству функций: ж_б (т) = 0.т_б. Функции ж _б(т) инъекции, кроме ж ₂(т). Эта функция будет изменена для создания взаимного соответствия между Т и р.

Построение биекции между Т и р

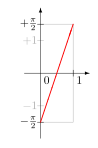
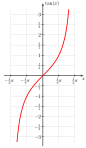
Функция час: (0,1) → (−π / 2, π / 2) Функция tan: (−π / 2, π / 2) → р В этой конструкции используется метод, разработанный Кантором, который был опубликован в 1878 году. Он использовал его для построения взаимного соответствия между закрытый интервал [0, 1] и иррациональные в открытый интервал (0, 1). Он сначала удалил счетно бесконечный подмножество из каждого из этих наборов, так что существует взаимно однозначное соответствие между оставшимися несчетными наборами. Поскольку между счетно бесконечными подмножествами, которые были удалены, существует взаимное соответствие, объединение двух взаимно однозначно приводит к взаимному соответствию между исходными наборами.[9] Метод Кантора можно использовать для изменения функции ж 2(т) = 0.т2 произвести биекцию из Т в (0, 1). Поскольку некоторые числа имеют два двоичных расширения, ж 2(т) даже не инъективный. Например, ж 2(1000…) = 0.1000...2 = 1/2 и ж 2(0111…) = 0.0111...2 = 1/4 + 1/8 + 1/16 + … = 1/2, поэтому и 1000 ... и 0111 ... отображаются на одно и то же число 1/2. Модифицировать ж2 (т)заметим, что это биекция, за исключением счетно бесконечного подмножества (0, 1) и счетно бесконечного подмножества Т. Это не биекция для чисел в (0, 1), которые имеют два двоичные расширения. Они называются диадический числа и имеют вид м / 2п куда м нечетное целое число и п натуральное число. Поместите эти числа в последовательность: р = (1/2, 1/4, 3/4, 1/8, 3/8, 5/8, 7/8, ...). Также, ж2 (т) не является биекцией к (0, 1) для строк в Т появившийся после двоичная точка в двоичных разложениях 0, 1 и чисел в последовательности р. Поместите эти в конечном итоге постоянные строки в последовательность: s = (000..., 111..., 1000..., 0111..., 01000..., 00111..., 11000..., 10111..., ...). Определите взаимное соответствие грамм(т) из Т to (0, 1): Если т это п^th строка в последовательности s, позволять грамм(т) быть п^th номер в последовательности р ; иначе, грамм(т) = 0.т2. Чтобы построить биекцию из Т к р, начнем с касательная функция загар (Икс), которая является биекцией из (−π / 2, π / 2) в р (см. рисунок справа). Затем заметьте, что линейная функция час(Икс) = πИкс - π / 2 является биекцией из (0, 1) в (−π / 2, π / 2) (см. рисунок слева). В составная функция загар (час(Икс)) = загар (πИкс - π / 2) является биекцией из (0, 1) в р. Составление этой функции с грамм(т) производит функцию tan (час(грамм(т))) = загар (πграмм(т) - π / 2), которое является биекцией из Т к р.

Общие наборы

Иллюстрация обобщенного диагонального аргумента: множество Т = {п∈ℕ: п∉ж(п)} внизу не может встречаться нигде в диапазоне ж:ℕ →п (ℕ). Пример отображения ж соответствует приведенному в примере перечислению s в над рисунок.

Обобщенная форма диагонального аргумента использовалась Кантором для доказательства Теорема кантора: для каждого набор S, то набор мощности из S- то есть набор всех подмножества из S (здесь написано как п(S)) - не может быть взаимно однозначно S сам. Это доказательство происходит следующим образом:

Позволять ж быть любым функция из S к п(S). Достаточно доказать ж не может быть сюръективный. Это означает, что какой-то член Т из п(S), т.е. некоторое подмножество S, не входит в изображение из ж. В качестве кандидата рассмотрим набор:

Т = { s ∈ S: s ∉ ж(s) }.

Для каждого s в S, либо s в Т или нет. Если s в Т, то по определению Т, s не в ж(s), так Т не равно ж(s). С другой стороны, если s не в Т, то по определению Т, s в ж(s), так что снова Т не равно ж(s); ср. Для более полного изложения этого доказательства см. Теорема кантора.

Последствия

Заказ кардиналов

Кантор определяет отношение порядка мощности, например ${\displaystyle |S|}$ и ${\displaystyle |T|}$, с точки зрения наличия инъекций между нижележащими множествами, ${\displaystyle S}$ и ${\displaystyle T}$. Аргумент в предыдущем абзаце затем доказал, что такие множества, как ${\displaystyle {\mathbb {N} }\to \{0,1\}}$ бесчисленны, то есть ${\displaystyle \neg (|{\mathbb {N} }\to \{0,1\}|\leq |{\mathbb {N} }|)}$, и мы можем вставить натуральные числа в функциональное пространство, так что мы имеем ${\displaystyle |{\mathbb {N} }|<|{\mathbb {N} }\to \{0,1\}|}$. В контексте классическая математика, это исчерпывает возможности, и диагональный аргумент может, таким образом, использоваться, чтобы установить, что, например, хотя оба рассматриваемых множества бесконечны, на самом деле существует более бесконечные последовательности единиц и нулей, чем натуральные числа. Этот результат также означает, что понятие набор всех наборов непоследовательно: если S были набором всех наборов, то п(S) в то же время будет больше, чем S и подмножество S.Предполагая закон исключенного среднего, каждый подсчетный множество (свойство в терминах сюръекций) тоже уже исчисляемо.

В Конструктивная математика, порядковые числа, а также кардиналы упорядочить сложнее или невозможно. Например, Теорема Шредера – Бернштейна. требует закона исключенного третьего. Порядок вещественных чисел (стандартный порядок, расширяющий порядок рациональных чисел) также не обязательно разрешим. Большинство свойств интересных классов функций также не разрешимы с помощью Теорема Райса, т.е. правильный набор счетных чисел для подсчетных множеств может не быть рекурсивный. В теории множеств теории математики смоделированный. Например, в теории множеств "набор действительных чисел" идентифицирован как набор, который выполняет некоторые аксиомы действительных чисел. Были изучены различные модели, такие как Дедекинд реалы или Реалы Коши. Более слабые аксиомы означают меньшее количество ограничений и, таким образом, позволяют использовать более богатый класс моделей. Следовательно, в конструктивном контексте (закон исключенного третьего не принимается в качестве аксиомы) целесообразно принимать неклассические аксиомы, которые противоречат следствиям закона исключенного третьего. Например, бесчисленное множество функций ${\displaystyle {\mathbb {N} }\to \{0,1\}}$ можно утверждать, что подсчетный, понятие размера, ортогональное утверждению ${\displaystyle |{\mathbb {N} }|<|{\mathbb {N} }\to \{0,1\}|}$.^[10] В таком контексте возможна субсчетность действительных чисел, что интуитивно позволяет получить более тонкий набор чисел, чем в других моделях.

Открытые вопросы

Мотивированный пониманием того, что набор действительных чисел «больше», чем набор натуральных чисел, возникает вопрос, существует ли набор, мощность находится "между" целыми числами и действительными. Этот вопрос приводит к известному гипотеза континуума. Точно так же вопрос о том, существует ли множество, мощность которого находится между |S| и |п(S) | для некоторых бесконечных S приводит к гипотеза обобщенного континуума.

Диагонализация в более широком контексте

Парадокс Рассела показал, что наивная теория множеств на основе неограниченное понимание схема, противоречивая. Обратите внимание, что есть сходство между построением Т и парадокс Рассела. Следовательно, в зависимости от того, как мы модифицируем схему понимания аксиом, чтобы избежать парадокса Рассела, такие аргументы, как несуществование набора всех наборов, могут или не могут оставаться действительными.

Аналоги диагонального аргумента широко используются в математике для доказательства существования или отсутствия определенных объектов. Например, обычное доказательство неразрешимости проблема остановки по сути диагональный аргумент. Кроме того, диагонализация изначально использовалась, чтобы показать существование произвольно жестких классы сложности и сыграл ключевую роль в первых попытках доказать P не равно NP.

Версия для новых основ Куайна

Приведенное выше доказательство не подходит для В. В. Куайн "s"Новые основы "теория множеств (НФ). В НФ схема понимания наивных аксиом доработан, чтобы избежать парадоксов, введен своего рода "локальный" теория типов. В этой схеме аксиом

{ s ∈ S: s ∉ ж(s) }

является нет набор - т.е.не удовлетворяет схеме аксиом. С другой стороны, мы могли бы попытаться создать модифицированный диагональный аргумент, заметив, что

{ s ∈ S: s ∉ ж({s}) }

является набор в НФ. В этом случае, если п₁(S) - множество одноэлементных подмножеств S и ж это предлагаемая биекция от п₁(S) к п(S), можно использовать доказательство от противного доказать, что |п₁(S)| < |п(S)|.

Доказательство следует из того, что если ж действительно были картой на п(S), тогда мы могли бы найти р в S, так что ж({р}) совпадает с модифицированным диагональным набором выше. Мы бы сделали вывод, что если р не в ж({р}), тогда р в ж({р}) наоборот.

это нет можно поставить п₁(S) во взаимно однозначном отношении с S, поскольку они имеют разные типы, и поэтому любая функция, определенная таким образом, нарушит правила набора для схемы понимания.

Смотрите также

• Первое доказательство несчетности Кантора
• Споры по теории Кантора
• Диагональная лемма

Рекомендации

1. Георг Кантор (1891). "Ueber eine elementare Frage der Mannigfaltigkeitslehre". Jahresbericht der Deutschen Mathematiker-Vereinigung. 1: 75–78. Английский перевод: Эвальд, Уильям Б. (редактор) (1996). От Иммануила Канта до Дэвида Гильберта: Справочник по основам математики, том 2. Издательство Оксфордского университета. С. 920–922. ISBN  0-19-850536-1.
2. Кейт Симмонс (30 июля 1993 г.). Универсальность и лжец: очерк истины и диагональный аргумент. Издательство Кембриджского университета. ISBN  978-0-521-43069-2.
3. Рудин, Вальтер (1976). Принципы математического анализа (3-е изд.). Нью-Йорк: Макгроу-Хилл. п.30. ISBN  0070856133.
4. Грей, Роберт (1994), «Георг Кантор и трансцендентные числа» (PDF), Американский математический ежемесячный журнал, 101 (9): 819–832, Дои:10.2307/2975129, JSTOR  2975129
5. Блох, Итан Д. (2011). Реальные числа и реальный анализ. Нью-Йорк: Спрингер. п.429. ISBN  978-0-387-72176-7.
6. Шеппард, Барнаби (2014). Логика бесконечности (иллюстрированный ред.). Издательство Кембриджского университета. п. 73. ISBN  978-1-107-05831-6. Отрывок страницы 73
7. «Парадокс Рассела». Стэнфордская энциклопедия философии.
8. Бертран Рассел (1931). Принципы математики. Нортон. С. 363–366.
9. См. Страницу 254 из Георг Кантор (1878), "Ein Beitrag zur Mannigfaltigkeitslehre", Journal für die Reine und Angewandte Mathematik, 84: 242–258. Это доказательство обсуждается в Джозеф Даубен (1979), Георг Кантор: его математика и философия бесконечного, Издательство Гарвардского университета, ISBN  0-674-34871-0, pp. 61–62, 65. На странице 65 Даубен доказывает результат, более сильный, чем результат Кантора. Он позволяет "φ_ν обозначают любую последовательность рациональных чисел в [0, 1] ». Кантор позволяет φ_ν обозначить последовательность перечисление рациональные числа в [0, 1], что является типом последовательности, необходимой для его построения биекции между [0, 1] и иррациональными числами в (0, 1).
10. Ратиен, М. "Принципы выбора в конструктивной и классической теории множеств ", Материалы коллоквиума по логике, 2002 г.

внешняя ссылка

• Диагональное доказательство Кантора на MathPages
• Вайсштейн, Эрик В. «Диагональный метод Кантора». MathWorld.