Гипотеза Андрикаса - Andricas conjecture

(а) Функция

{ displaystyle A_ {n}}

для первых 100 простых чисел.

(б) Функция

{ displaystyle A_ {n}}

для первых 200 простых чисел.

(c) Функция

{ displaystyle A_ {n}}

для первых 500 простых чисел.

Графическое доказательство гипотезы Андрицы для первых (а) 100, (б) 200 и (в) 500 простых чисел. Предполагается, что функция

{ displaystyle A_ {n}}

всегда меньше 1.

Гипотеза Андрицы (названный в честь Дорин Андрица ) это догадка взяв во внимание пробелы между простые числа.^[1]

Гипотеза утверждает, что неравенство

{ displaystyle { sqrt {p_ {n + 1}}} - { sqrt {p_ {n}}} <1}

относится ко всем ${ displaystyle n}$ , куда ${ displaystyle p_ {n}}$ это пое простое число. Если ${ displaystyle g_ {n} = p_ {n + 1} -p_ {n}}$ обозначает пth основной разрыв, то гипотезу Андрицы также можно переписать в виде

{ displaystyle g_ {n} <2 { sqrt {p_ {n}}} + 1.}

Эмпирическое доказательство

Имран Гори использовал данные о наибольших разрывах между простыми числами, чтобы подтвердить гипотезу для ${ displaystyle n}$ до 1,3002 × 10¹⁶.^[2] Используя таблицу максимальные зазоры и указанное выше неравенство разрыва, значение подтверждения может быть полностью расширено до 4 × 10¹⁸.

Дискретная функция ${ displaystyle A_ {n} = { sqrt {p_ {n + 1}}} - { sqrt {p_ {n}}}}$ изображен на рисунках напротив. Высшие отметки для ${ displaystyle A_ {n}}$ происходить для п = 1, 2 и 4, причем А₄ ≈ 0,670873 ..., среди первых 10⁵ простые числа. Поскольку функция Андрика убывает асимптотически в качестве п увеличивается, необходим простой промежуток все увеличивающегося размера, чтобы разница была большой, поскольку п становится большим. Поэтому представляется весьма вероятным, что эта гипотеза верна, хотя это еще не доказано.

Обобщения

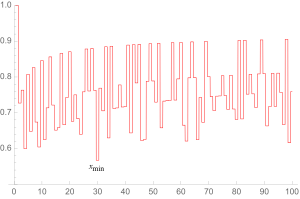
Значение Икс в обобщенной гипотезе Андрицы для первых 100 простых чисел с предполагаемым значением Икс_мин помечены.

В качестве обобщения гипотезы Андрицы было рассмотрено следующее уравнение:

{ displaystyle p_ {n + 1} ^ {x} -p_ {n} ^ {x} = 1,}

куда ${ displaystyle p_ {n}}$ это пй премьер и Икс может быть любым положительным числом.

Максимально возможное решение для Икс легко увидеть, что происходит для п= 1, когда Икс_{Максимум} = 1. Наименьшее решение для Икс предполагается, что это Икс_мин ≈ 0,567148 ... (последовательность A038458 в OEIS ) что происходит для п = 30.

Эта гипотеза также была высказана как неравенство, обобщенная гипотеза Андрицы:

{ displaystyle p_ {n + 1} ^ {x} -p_ {n} ^ {x} <1}

за

{ displaystyle x

Смотрите также

Ссылки и примечания

^ Андрица, Д. (1986). «Замечание о гипотезе в теории простых чисел». Studia Univ. Babes – Bolyai Math. 31 (4): 44–48. ISSN 0252-1938. Zbl 0623.10030.
^ Простые числа: самые загадочные числа в математике, John Wiley & Sons, Inc., 2005, стр. 13.

Гай, Ричард К. (2004). Нерешенные проблемы теории чисел (3-е изд.). Springer-Verlag. ISBN 978-0-387-20860-2. Zbl 1058.11001.

внешняя ссылка

[1] Андрица, Д. (1986). «Замечание о гипотезе в теории простых чисел». Studia Univ. Babes – Bolyai Math. 31 (4): 44–48. ISSN 0252-1938. Zbl 0623.10030.

[2] Простые числа: самые загадочные числа в математике, John Wiley & Sons, Inc., 2005, стр. 13.

[1]

[2]