Адиабатический процесс - Adiabatic process

В термодинамика, адиабатический процесс это тип термодинамический процесс которое происходит без передачи высокая температура или же масса между система и это окружение. В отличие от изотермический процесс, адиабатический процесс передает энергию в окружающую среду только как работай.^[1]^[2] Он также концептуально поддерживает теорию, используемую для объяснения первый закон термодинамики и поэтому является ключевым термодинамический концепция.

Некоторые химические и физические процессы происходят слишком быстро, чтобы энергия могла войти в систему или покинуть ее в виде тепла, что позволяет использовать удобное «адиабатическое приближение».^[3] Например, адиабатическая температура пламени использует это приближение для вычисления верхнего предела пламя температура, предполагая, что сгорание не теряет тепла в окружающую среду.

В метеорология и океанография, адиабатическое охлаждение вызывает конденсацию влаги или солености, перенасыщая посылка. Поэтому лишнее нужно убрать. Там процесс становится псевдоадиабатический процесс при этом предполагается, что жидкая вода или соль, которая конденсируется, удаляются при образовании идеализированным мгновенным осадки. Псевдоадиабатический процесс определяется только для расширения, поскольку сжатый участок становится теплее и остается недонасыщенным.^[4]

Описание

Процесс без передачи тепла или вещества в систему или из системы, так что $Q = 0$ , называется адиабатической, и такая система называется адиабатически изолированной.^[5]^[6] Предположение, что процесс является адиабатическим, часто делается упрощающим предположением. Например, предполагается, что сжатие газа в цилиндре двигателя происходит настолько быстро, что в масштабе времени процесса сжатия небольшая часть энергии системы может передаваться в виде тепла в окружающую среду. Несмотря на то, что цилиндры не изолированы и обладают достаточной проводимостью, этот процесс идеализирован как адиабатический. То же самое можно сказать и о процессе расширения такой системы.

Предположение об адиабатической изоляции полезно и часто сочетается с другими подобными идеализациями для расчета хорошего первого приближения поведения системы. Например, согласно Лаплас, когда звук распространяется в газе, нет времени для теплопроводности в среде, и поэтому распространение звука является адиабатическим. Для такого адиабатического процесса модуль упругости (Модуль для младших ) можно выразить как $E = γP$ , куда $γ$ это соотношение удельных теплоемкостей при постоянном давлении и постоянном объеме ( $γ = C п / C v$ ) и $п$ давление газа.

Различные приложения адиабатического предположения

Для закрытой системы можно написать первый закон термодинамики в качестве : $Δ U = Q - W$ , куда $Δ U$ обозначает изменение внутренней энергии системы, $Q$ количество энергии, добавленной к нему в виде тепла, и $W$ работа, проделанная системой с окружающей средой.

Если в системе такие жесткие стены, что работа не может быть перенесена внутрь или наружу ( $W = 0$ ), а стенки не адиабатические, и энергия добавляется в виде тепла ( $Q > 0$ ), и фазового перехода нет, то температура системы повысится.
Если система имеет такие жесткие стенки, что работа давления и объема не может выполняться, но стенки адиабатические ( $Q = 0$ ), а энергия добавляется в виде изохорной работы в форме трения или перемешивания вязкой жидкости внутри системы ( $W < 0$ ), и фазового перехода нет, то температура системы повысится.
Если стенки системы адиабатические ( $Q = 0$ ) но не жесткий ( $W \neq 0$ ), а в фиктивном идеализированном процессе к системе добавляется энергия в виде невязкой работы давления и объема без трения ( $W < 0$ ), и фазового перехода нет, то температура системы повысится. Такой процесс называется изэнтропический процесс и называется «обратимым». Фактически, если бы процесс был обращен вспять, энергия могла бы быть полностью восстановлена как работа, выполняемая системой. Если система содержит сжимаемый газ и ее объем уменьшается, неопределенность положения газа уменьшается и, по-видимому, уменьшится энтропия системы, но температура системы будет расти, поскольку процесс является изоэнтропическим ( $Δ S = 0$ ). Если работа добавляется таким образом, что в системе действуют силы трения или вязкости, тогда процесс не является изоэнтропическим, а если нет фазового перехода, тогда температура системы повышается, процесс называется "необратимые", и работа, добавленная в систему, не может быть полностью восстановлена в виде работы.
Если стенки системы не адиабатические и энергия передается в виде тепла, энтропия передается системе вместе с теплом. Такой процесс не является ни адиабатическим, ни изэнтропическим, поскольку $Q > 0$ , и $Δ S > 0$ согласно второй закон термодинамики.

Естественные адиабатические процессы необратимы (создается энтропия).

Передачу энергии как работы в адиабатически изолированную систему можно представить как два идеализированных крайних вида. В одном из таких случаев энтропия не создается внутри системы (нет трения, вязкой диссипации и т. Д.), И работа представляет собой только работу объема давления (обозначается как $п d V$ ). В природе этот идеальный вид встречается только приблизительно, потому что он требует бесконечно медленного процесса и отсутствия источников рассеяния.

Другой крайний вид работы - это изохорная работа ( $d V = 0$ ), для которых энергия добавляется как работа исключительно за счет трения или вязкого рассеяния внутри системы. Мешалка, которая передает энергию вязкой жидкости адиабатически изолированной системы с жесткими стенками без фазового перехода, вызовет повышение температуры жидкости, но эту работу невозможно восстановить. Изохорическая работа необратима.^[7] Второй закон термодинамики отмечает, что естественный процесс передачи энергии как работы всегда состоит, по крайней мере, из изохорной работы, а часто и из этих крайних видов работы. Любой естественный процесс, адиабатический или нет, необратим, с $Δ S > 0$ , поскольку трение или вязкость в той или иной степени присутствуют всегда.

Адиабатический нагрев и охлаждение

Адиабатическое сжатие газа вызывает повышение температуры газа. Адиабатическое расширение против давления или пружины вызывает падение температуры. В отличие, бесплатное расширение является изотермический процесс для идеального газа.

Адиабатический нагрев возникает, когда давление газа увеличивается в результате работы, выполняемой над ним окружающей средой, например, поршень сжатие газа, содержащегося в цилиндре, и повышение температуры, при этом во многих практических ситуациях теплопроводность через стенки может быть медленной по сравнению со временем сжатия. Это находит практическое применение в дизельные двигатели которые основаны на отсутствии тепловыделения во время такта сжатия для повышения температуры паров топлива в достаточной степени для его воспламенения.

Адиабатический нагрев происходит в Атмосфера Земли когда масса воздуха спускается, например, в стоковый ветер, Фен ветра, или же чавычи ветер течет вниз по горному хребту. Когда посылка воздуха опускается, давление на посылку увеличивается. Из-за этого увеличения давления объем пакета уменьшается, а его температура увеличивается по мере выполнения работы с пакетом воздуха, тем самым увеличивая его внутреннюю энергию, что проявляется в повышении температуры этой массы воздуха. Частица воздуха может лишь медленно рассеивать энергию за счет теплопроводности или излучения (тепла), и в первом приближении ее можно считать адиабатически изолированной, а процесс - адиабатическим процессом.

Адиабатическое охлаждение возникает, когда давление на адиабатически изолированную систему уменьшается, позволяя ей расширяться, заставляя, таким образом, работать со своим окружением. Когда давление, оказываемое на посылку с воздухом, уменьшается, воздух в посылке может расширяться; по мере увеличения объема температура падает по мере уменьшения его внутренней энергии. В атмосфере Земли происходит адиабатическое охлаждение с орографический лифтинг и подветренные волны, и это может образовывать пилеус или же линзовидные облака.

Для адиабатического охлаждения не обязательно использовать жидкость. Один метод, используемый для достижения очень низких температур (тысячных и даже миллионных долей градуса выше абсолютного нуля), - это адиабатическое размагничивание, где изменение магнитное поле на магнитном материале используется для обеспечения адиабатического охлаждения. Кроме того, содержимое расширяющаяся вселенная можно описать (в первом порядке) как адиабатически охлаждающую жидкость. (Видеть тепловая смерть вселенной.)

Поднимающаяся магма также подвергается адиабатическому охлаждению перед извержением, что особенно важно в случае магм, которые быстро поднимаются с больших глубин, таких как кимберлиты.^[8]

В конвектирующей мантии Земли (астеносфере) под литосферой температура мантии приблизительно равна адиабате. Незначительное снижение температуры с уменьшением глубины связано с тем, что давление уменьшается по мере того, как на Земле мельче находится материал.^[9]

Такие изменения температуры можно количественно оценить с помощью закон идеального газа, или уравнение гидростатики для атмосферных процессов.

На практике ни один процесс не является по-настоящему адиабатическим. Многие процессы зависят от большой разницы во временных масштабах интересующего процесса и скорости рассеивания тепла через границу системы и, таким образом, аппроксимируются с помощью адиабатического предположения. Всегда есть некоторая потеря тепла, так как идеальных изоляторов не существует.

Идеальный газ (обратимый процесс)

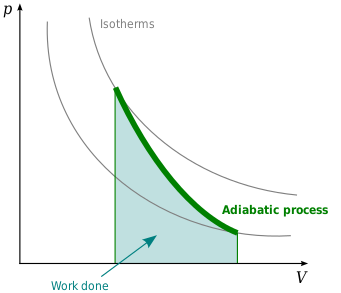
Для простого вещества во время адиабатического процесса увеличения объема внутренняя энергия рабочего вещества должно уменьшиться

Математическое уравнение для идеальный газ претерпевающий обратимый (т.е. без генерации энтропии) адиабатический процесс может быть представлен политропный процесс уравнение^[3]

{displaystyle PV ^ {gamma} = {ext {constant}},}

куда $п$ давление, $V$ объем, и в этом случае $п = γ$ , куда

{displaystyle gamma = {frac {C_ {P}} {C_ {V}}} = {frac {f + 2} {f}},}

$C п$ будучи удельная теплоемкость для постоянного давления, $C V$ удельная теплоемкость при постоянном объеме, $γ$ это индекс адиабаты, и $ж$ это количество степени свободы (3 для одноатомного газа, 5 для двухатомного газа и коллинеарных молекул, например, двуокиси углерода).

Для одноатомного идеального газа $γ = 5 / 3$ , а для двухатомного газа (например, азот и кислород, основные компоненты воздуха) $γ = 7 / 5$ .^[10] Обратите внимание, что приведенная выше формула применима только к классическим идеальным газам, а не к Бозе-Эйнштейн или же Ферми-газы.

Для обратимых адиабатических процессов верно также, что^[3]

{displaystyle P ^ {1-gamma} T ^ {gamma} = {ext {constant}},}

{displaystyle VT ^ {frac {f} {2}} = {ext {constant}},}

куда Т абсолютная температура. Это также можно записать как^[3]

{displaystyle TV ^ {gamma -1} = {ext {constant}}.}

Пример адиабатического сжатия

Ход сжатия в бензиновый двигатель можно использовать как пример адиабатического сжатия. Предположения модели: несжатый объем баллона - один литр (1 л = 1000 см³ = 0,001 м³); газ внутри - это воздух, состоящий только из молекулярного азота и кислорода (таким образом, двухатомный газ с 5 степенями свободы и т. $γ = 7 / 5$ ); степень сжатия двигателя - 10: 1 (то есть объем 1 л несжатого газа уменьшен поршнем до 0,1 л); а несжатый газ имеет приблизительно комнатную температуру и давление (теплая комнатная температура ~ 27 ° C, или 300 K, и давление 1 бар = 100 кПа, то есть типичное атмосферное давление на уровне моря).

{displaystyle P_ {1} V ^ {gamma} = operatorname {constant} _ {1} = 100 000 ~ {ext {Pa}} время (0,001 ~ {ext {m}} ^ {3}) ^ {frac {7} {5}}}

{displaystyle = 10 ^ {5} imes 6.31 imes 10 ^ {- 5} ~ {ext {Pa}}, {ext {m}} ^ {21/5} = 6.31 ~ {ext {Pa}}, {ext { m}} ^ {21/5},}

поэтому наша адиабатическая постоянная для этого примера составляет около 6,31 Па · м^4.2.

Теперь газ сжат до 0,1 л (0,0001 м³) объема (предположим, что это происходит достаточно быстро, чтобы тепло не могло проникнуть или покинуть газ через стены). Постоянная адиабаты остается прежней, но результирующее давление неизвестно.

{displaystyle P_ {2} V ^ {gamma} = operatorname {constant} _ {1} = 6.31 ~ {ext {Pa}}, {ext {m}} ^ {21/5} = P imes (0,0001 ~ {ext {m}} ^ {3}) ^ {frac {7} {5}},}

так решение для п₂:

{displaystyle P_ {2} = {frac {6.31 ~ {ext {Pa}}, {ext {m}} ^ {21/5}} {(0.0001 ~ {ext {m}} ^ {3}) ^ {frac {7} {5}}}} = {frac {6.31 ~ {ext {Pa}}, {ext {m}} ^ {21/5}} {2.5 imes 10 ^ {- 6} ~ {ext {m} } ^ {21/5}}} = 2,51 раза 10 ^ {6} ~ {ext {Pa}},}

или 25,1 бар. Обратите внимание, что это увеличение давления больше, чем может указывать простая степень сжатия 10: 1; это связано с тем, что газ не только сжимается, но и работа, выполняемая для сжатия газа, также увеличивает его внутреннюю энергию, что проявляется в повышении температуры газа и дополнительном повышении давления выше того, что было бы в результате упрощенного расчета 10 раз первоначальное давление.

Мы также можем определить температуру сжатого газа в цилиндре двигателя, используя закон идеального газа: PV = nRT (п количество газа в молях и р газовая постоянная для этого газа). Наши начальные условия: давление 100 кПа, объем 1 л и температура 300 K, наша экспериментальная постоянная (nR) является:

{displaystyle {frac {PV} {T}} = operatorname {constant} _ {2} = {frac {10 ^ {5} ~ {ext {Pa}} раз 10 ^ {- 3} ~ {ext {m}} ^ {3}} {300 ~ {ext {K}}}} = 0,333 ~ {ext {Pa}}, {ext {m}} ^ {3} {ext {K}} ^ {- 1}.}

Мы знаем, что сжатый газ $V$ = 0,1 л и $п$ = 2.51×10⁶ Па, поэтому мы можем найти температуру:

{displaystyle T = {frac {PV} {operatorname {constant} _ {2}}} = {frac {2,51 imes 10 ^ {6} ~ {ext {Pa}} imes 10 ^ {- 4} ~ {ext {m }} ^ {3}} {0.333 ~ {ext {Pa}}, {ext {m}} ^ {3} {ext {K}} ^ {- 1}}} = 753 ~ {ext {K}}. }

Это конечная температура 753 K, или 479 ° C, или 896 ° F, что намного выше точки воспламенения многих видов топлива. Вот почему двигатель с высокой степенью сжатия требует топлива, специально разработанного для предотвращения самовоспламенения (что может вызвать стук двигателя при работе в этих условиях температуры и давления), или что нагнетатель с интеркулер для обеспечения повышения давления, но с меньшим повышением температуры, было бы выгодно. Дизельный двигатель работает в еще более экстремальных условиях, с типичной степенью сжатия 16: 1 или более, чтобы обеспечить очень высокую температуру газа, которая обеспечивает немедленное воспламенение впрыскиваемого топлива.

Свободное адиабатическое расширение газа

Для адиабатического свободного расширения идеального газа газ содержится в изолированном контейнере, а затем расширяется в вакууме. Поскольку нет внешнего давления для расширения газа, работа, выполняемая системой или над ней, равна нулю. Поскольку этот процесс не включает в себя передачу тепла или работу, первый закон термодинамики подразумевает, что чистое изменение внутренней энергии системы равно нулю. Для идеального газа температура остается постоянной, поскольку в этом случае внутренняя энергия зависит только от температуры. Поскольку при постоянной температуре энтропия пропорциональна объему, энтропия в этом случае увеличивается, поэтому этот процесс необратим.

Вывод п–V соотношение для адиабатического нагрева и охлаждения

Определение адиабатического процесса состоит в том, что передача тепла системе равна нулю, $δQ = 0$ . Тогда, согласно первому закону термодинамики,

{displaystyle {ext {(1)}} qquad dU + delta W = delta Q = 0,}

куда $dU$ - изменение внутренней энергии системы и $δW$ работа сделана к система. Любая работа ( $δW$ ) делать надо за счет внутренней энергии $U$ , так как нет тепла $δQ$ подается из окрестностей. Давление – объемная работа $δW$ сделано к система определяется как

{displaystyle {ext {(2)}} qquad delta W = P, dV.}

Тем не мение, $п$ не остается постоянным во время адиабатического процесса, а вместо этого изменяется вместе с $V$ .

Желательно знать, как значения $dP$ и $dV$ связаны друг с другом по мере протекания адиабатического процесса. Для идеального газа (вспомните закон идеального газа $PV = nRT$ ) внутренняя энергия определяется выражением

{displaystyle {ext {(3)}} qquad U = alpha nRT = alpha PV,}

куда $α$ число степеней свободы, деленное на два, $р$ это универсальная газовая постоянная и $п$ - количество молей в системе (постоянная величина).

Дифференцируя уравнение (3), получаем

{displaystyle {ext {(4)}} qquad dU = alpha nR, dT = alpha, d (PV) = alpha (P, dV + V, dP).}

Уравнение (4) часто выражается как $dU = nC V dT$ потому что $C V = αR$ .

Теперь подставьте уравнения (2) и (4) в уравнение (1), чтобы получить

{displaystyle -P, dV = alpha P, dV + alpha V, dP,}

факторизовать $- P dV$ :

{displaystyle - (альфа +1) P, dV = альфа V, dP,}

и разделите обе стороны на $PV$ :

{displaystyle - (alpha +1) {frac {dV} {V}} = alpha {frac {dP} {P}}.}

После интеграции левой и правой частей из $V 0$ к $V$ и из $п 0$ к $п$ и меняя стороны соответственно,

{displaystyle ln left ({frac {P} {P_ {0}}} ight) = - {frac {alpha +1} {alpha}} ln left ({frac {V} {V_ {0}}} ight). }

Возводите в степень обе стороны, подставьте $α + 1 / α$ с $γ$ , коэффициент теплоемкости

{displaystyle left ({frac {P} {P_ {0}}} ight) = left ({frac {V} {V_ {0}}} ight) ^ {- gamma},}

и удалите отрицательный знак, чтобы получить

{displaystyle left ({frac {P} {P_ {0}}} ight) = left ({frac {V_ {0}} {V}} ight) ^ {gamma}.}

Следовательно,

{displaystyle left ({frac {P} {P_ {0}}} ight) left ({frac {V} {V_ {0}}} ight) ^ {gamma} = 1,}

и

{displaystyle P_ {0} V_ {0} ^ {gamma} = PV ^ {gamma} = имя оператора {константа}.}

Вывод п–Т соотношение для адиабатического нагрева и охлаждения

Подставляя закон идеального газа в вышеизложенное, получаем

{displaystyle Pleft ({frac {nRT} {P}} ight) ^ {gamma} = имя оператора {константа},}

что упрощает

{displaystyle P ^ {1-gamma} T ^ {gamma} = имя оператора {константа}.}

Вывод дискретной формулы и рабочего выражения

Изменение внутренней энергии системы, измеренное от состояния 1 к состоянию 2, равно

{displaystyle {ext {(1)}} qquad Delta U = alpha RnT_ {2} -alpha RnT_ {1} = alpha RnDelta T.}

В то же время работа, совершаемая изменением давления – объема в результате этого процесса, равна

{displaystyle {ext {(2)}} qquad W = int _ {V_ {1}} ^ {V_ {2}} P, dV.}

Поскольку мы требуем, чтобы процесс был адиабатическим, должно выполняться следующее уравнение

{displaystyle {ext {(3)}} qquad Delta U + W = 0.}

По предыдущему выводу,

{displaystyle {ext {(4)}} qquad PV ^ {gamma} = {ext {constant}} = P_ {1} V_ {1} ^ {gamma}.}

Перестановка (4) дает

{displaystyle P = P_ {1} left ({frac {V_ {1}} {V}} ight) ^ {gamma}.}

Подставляя это в (2), получаем

{displaystyle W = int _ {V_ {1}} ^ {V_ {2}} P_ {1} left ({frac {V_ {1}} {V}} ight) ^ {gamma}, dV.}

Интегрируя, получаем выражение для работы:

{displaystyle W = P_ {1} V_ {1} ^ {gamma} {frac {V_ {2} ^ {1-gamma} -V_ {1} ^ {1-gamma}} {1-gamma}} = {frac {P_ {2} V_ {2} -P_ {1} V_ {1}} {1-gamma}}.}

Подстановка $γ = α + 1 / α$ во второй срок,

{displaystyle W = -alpha P_ {1} V_ {1} ^ {gamma} left (V_ {2} ^ {1-gamma} -V_ {1} ^ {1-gamma} ight).}

Перестановка,

{displaystyle W = -alpha P_ {1} V_ {1} left (left ({frac {V_ {2}} {V_ {1}}} ight) ^ {1-gamma} -1ight).}

Используя закон идеального газа и предполагая постоянное молярное количество (как часто бывает на практике),

{displaystyle W = -alpha nRT_ {1} left (left ({frac {V_ {2}} {V_ {1}}} ight) ^ {1-gamma} -1ight).}

По непрерывной формуле

{displaystyle {frac {P_ {2}} {P_ {1}}} = left ({frac {V_ {2}} {V_ {1}}} ight) ^ {- gamma},}

или же

{displaystyle left ({frac {P_ {2}} {P_ {1}}} ight) ^ {- {frac {1} {gamma}}}} = {frac {V_ {2}} {V_ {1}}} .}

Подставляя в предыдущее выражение для $W$ ,

{displaystyle W = -alpha nRT_ {1} left (left ({frac {P_ {2}} {P_ {1}}} ight) ^ {frac {gamma -1} {gamma}} - 1ight).}

Подставляя это выражение и (1) в (3), получаем

{displaystyle alpha nR (T_ {2} -T_ {1}) = alpha nRT_ {1} left (left ({Frac {P_ {2}} {P_ {1}}} ight) ^ {frac {gamma -1}) {gamma}} - 1 ночь).}

Упрощение,

{displaystyle T_ {2} -T_ {1} = T_ {1} left (left ({frac {P_ {2}} {P_ {1}}} ight) ^ {frac {gamma -1} {gamma}}) - 1 ночь),}

{displaystyle {frac {T_ {2}} {T_ {1}}} - 1 = left ({frac {P_ {2}} {P_ {1}}} ight) ^ {frac {gamma -1} {gamma}) } -1,}

{displaystyle T_ {2} = T_ {1} left ({frac {P_ {2}} {P_ {1}}} ight) ^ {frac {gamma -1} {gamma}}.}

Графические адиабаты

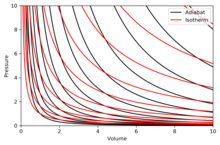
Адиабата - это кривая постоянного энтропия на диаграмме. Некоторые свойства адиабат на п–V схемы указаны. Эти свойства можно прочитать из классического поведения идеальных газов, за исключением области, где PV становится малым (низкая температура), где становятся важными квантовые эффекты.

Каждая адиабата асимптотически подходит как к V ось и п ось (как и изотермы ).
Каждая адиабата пересекает каждую изотерму ровно один раз.
Адиабата похожа на изотерму, за исключением того, что во время расширения адиабата теряет больше давления, чем изотерма, поэтому она имеет более крутой наклон (более вертикальный).
Если изотермы вогнуты в северо-восточном направлении (45 °), то адиабаты вогнуты в восточном северо-восточном направлении (31 °).
Если адиабаты и изотермы нанесены на график с регулярными интервалами энтропии и температуры, соответственно (например, высота на контурной карте), то по мере того, как глаз движется к осям (к юго-западу), он видит, что плотность изотерм остается постоянной, но он видит рост плотности адиабат. Исключение составляет очень близкий к абсолютному нулю, когда плотность адиабат резко падает, и они становятся редкими (см. Теорема Нернста ).^{[требуется разъяснение ]}

Правая диаграмма - это п–V диаграмма с наложением адиабат и изотерм:

Изотермы представляют собой красные кривые, а адиабаты - черные кривые.

Адиабаты изоэнтропичны.

Объем - по горизонтальной оси, а давление - по вертикальной оси.

Этимология

Период, термин адиабатический (/ˌædяəˈбæтɪk/) представляет собой англицизацию Греческий термин ἀδιάβατος «непроходимый» (используется Ксенофонт рек) .Это используется в термодинамическом смысле Ренкин (1866),^[11]^[12] и принят Максвелл в 1871 году (явно приписывая термин Рэнкину).^[13]Этимологическое происхождение здесь соответствует невозможности передача энергии в виде тепла и переноса материи через стену.

Греческое слово ἀδιάβατος образовано от приватный ἀ- («не») и διαβατός, «проходимый», в свою очередь происходящее от διά («через») и βαῖνειν («идти, идти, приходить»).^[14]

Концептуальное значение в термодинамической теории

Адиабатический процесс был важен для термодинамики с первых дней ее существования. Это было важно в работе Джоуля, поскольку позволяло почти напрямую связывать количество тепла и работы.

Энергия может входить или выходить из термодинамической системы, окруженной стенами, препятствующими массообмен только как тепло или работать. Следовательно, количество работы в такой системе может быть почти напрямую связано с эквивалентным количеством тепла в цикле двух конечностей. Первая часть представляет собой изохорный адиабатический рабочий процесс, увеличивающий внутренняя энергия; во-вторых, изохорный и неработающий теплообмен, возвращающий систему в исходное состояние. Соответственно, Ренкин измерял количество тепла в единицах работы, а не как калориметрическую величину.^[15] В 1854 году Ренкин использовал величину, которую он назвал «термодинамической функцией», которая позже была названа энтропией, и в то же время он написал также о «кривой отсутствия передачи тепла»,^[16] которую он позже назвал адиабатической кривой.^[11] Помимо двух изотермических ветвей, цикл Карно имеет два адиабатических элемента.

Для основ термодинамики концептуальную важность этого подчеркивал Брайан:^[17] от Каратеодори,^[1] и от Борна.^[18] Причина в том, что калориметрия предполагает тип температуры, который уже определен до утверждения первого закона термодинамики, например, основанный на эмпирических шкалах. Такое предположение включает различие между эмпирической температурой и абсолютной температурой. Скорее, определение абсолютной термодинамической температуры лучше оставить до тех пор, пока второй закон не станет доступным в качестве концептуальной основы.^[19]

В восемнадцатом веке закон сохранения энергии еще не был полностью сформулирован или установлен, а природа тепла обсуждалась. Один из подходов к этим проблемам заключался в том, чтобы рассматривать тепло, измеренное калориметрическим методом, как основное вещество, количество которого сохраняется. К середине девятнадцатого века он был признан формой энергии, и тем самым был признан закон сохранения энергии. Точка зрения, которая в конечном итоге утвердилась и в настоящее время считается правильной, состоит в том, что закон сохранения энергии является первичной аксиомой, и что тепло следует анализировать как следствие. В этом свете тепло не может быть составной частью общей энергии отдельного тела, потому что это не переменная состояния а, скорее, переменная, описывающая переход между двумя телами. Адиабатический процесс важен, потому что он является логической составляющей нынешней точки зрения.^[19]

Дивергентные употребления слова адиабатический

Настоящая статья написана с точки зрения макроскопической термодинамики, и слово адиабатический В этой статье используется традиционный метод термодинамики, введенный Рэнкином. В настоящей статье указывается, что, например, если сжатие газа происходит быстро, то для передачи тепла остается мало времени, даже если газ не адиабатически изолирован определенной стенкой. В этом смысле быстрое сжатие газа иногда приблизительно или в общих чертах называют адиабатический, хотя часто далеко от изоэнтропии, даже когда газ не адиабатически изолирован определенной стенкой.

Квантовая механика и квантовая статистическая механика однако используйте слово адиабатический в совсем другом смысле, который иногда может показаться почти противоположным классическому термодинамическому смыслу. В квантовой теории слово адиабатический может означать что-то, возможно, близкое к изоэнтропическому или, возможно, почти квазистатическое, но использование этого слова в этих двух дисциплинах сильно различается.

С одной стороны, в квантовой теории, если пертурбативный элемент сжимающей работы выполняется почти бесконечно медленно (то есть квазистатически), говорят, что он был выполнен. адиабатически. Идея состоит в том, что формы собственных функций меняются медленно и непрерывно, так что квантовый скачок не происходит, и изменение практически обратимо. Хотя числа заполнения не изменяются, тем не менее, есть изменение уровней энергии взаимно однозначных соответствующих собственных состояний до и после сжатия. Таким образом, пертурбативный элемент работы был выполнен без передачи тепла и без внесения случайных изменений в систему. Например, Макс Борн пишет: «На самом деле, это обычно« адиабатический »случай, с которым мы имеем дело: то есть предельный случай, когда внешняя сила (или реакция частей системы друг на друга) действует очень медленно. В этом случае, чтобы очень высокое приближение

{displaystyle c_ {1} ^ {2} = 1 ,,, c_ {2} ^ {2} = 0 ,,, c_ {3} ^ {2} = 0 ,, ... ,,}

то есть вероятность перехода отсутствует, и система находится в исходном состоянии после прекращения возмущения. Следовательно, такое медленное возмущение обратимо, как и в классическом смысле ".^[20]

С другой стороны, в квантовой теории, если пертурбативный элемент сжимающей работы выполняется быстро, он случайным образом изменяет числа заполнения собственных состояний, а также меняет их форму. В этой теории считается, что такое быстрое изменение недопустимо. адиабатический, и противоположное слово диабетический применяется к нему. Можно было бы предположить, что, возможно, Клаузиус, если бы он столкнулся с этим, на устаревшем языке, который он использовал в свое время, сказал бы, что «внутренняя работа» была сделана и что «тепло генерировалось, но не передавалось».^{[нужна цитата ]}

Более того, в атмосферной термодинамике диабатический процесс - это процесс, в котором происходит обмен теплом.^[21]

В классической термодинамике такое быстрое изменение все еще можно было бы назвать адиабатическим, потому что система адиабатически изолирована и нет передачи энергии в виде тепла. Сильная необратимость изменения из-за вязкости или другого производства энтропии не влияет на это классическое использование.

Таким образом, для массы газа в макроскопической термодинамике используются такие слова, что сжатие иногда в общих чертах или приблизительно называют адиабатическим, если оно достаточно быстрое, чтобы избежать передачи тепла, даже если система не является адиабатически изолированной. Но в квантовой статистической теории сжатие не называется адиабатическим, если оно быстрое, даже если система адиабатически изолирована в классическом термодинамическом смысле этого слова. Слова используются по-разному в этих двух дисциплинах, как указано выше.

Смотрите также

Связанные темы физики

Связанные термодинамические процессы

внешняя ссылка

СМИ, связанные с Адиабатические процессы в Wikimedia Commons

Статья в энциклопедии HyperPhysics

[Carathéodory-1] а ^б Каратеодори, К. (1909). "Untersuchungen über die Grundlagen der Thermodynamik". Mathematische Annalen. 67 (3): 355–386. Дои:10.1007 / BF01450409.. Перевод можно найти Вот В архиве 2019-10-12 в Wayback Machine. Также в основном надежный перевод должен быть найден в Кестин, Дж. (1976). Второй закон термодинамики. Страудсбург, Пенсильвания: Дауден, Хатчинсон и Росс.

[Bailyn_21-2] Байлын, М. (1994). Обзор термодинамики. Нью-Йорк, штат Нью-Йорк: Американский институт физики Press. п. 21. ISBN 0-88318-797-3.

[Bailyn_53-3] а ^б ^c ^d Байлин, М. (1994), стр. 52–53.

[4] «псевдоадиабатический процесс». Американское метеорологическое общество. Получено 3 ноября, 2018.

[5] Тиса, Л. (1966). Обобщенная термодинамика. Кембридж, Массачусетс: MIT Press. п. 48. (адиабатические перегородки препятствуют передаче тепла и массы)

[6] Мюнстер, А. (1970), стр. 48: «Масса - это адиабатически подавляемая переменная».

[7] Мюнстер, А. (1970). Классическая термодинамика. Перевод Хальберштадта, Э. С. Лондон: Wiley – Interscience. п. 45. ISBN 0-471-62430-6.

[Kavanagh-8] Kavanagh, J. L .; Спаркс, Р. С. Дж. (2009). «Температурные изменения восходящих кимберлитовых магм». Письма по науке о Земле и планетах. Эльзевир. 286 (3–4): 404–413. Bibcode:2009E и PSL.286..404K. Дои:10.1016 / j.epsl.2009.07.011. Получено 18 февраля 2012.

[9] Тюркотт и Шуберт (2002). Геодинамика. Кембридж: Издательство Кембриджского университета. стр.185. ISBN 0-521-66624-4.

[10] Адиабатические процессы.

[Rankine_1866-11] а ^б Рэнкин, У. Дж. МакКью. (1866 г.). По теории взрывных газовых двигателей, Инженер, 27 июля 1866 г .; на странице 467 перепечатки в Разные научные статьи, отредактированный У. Дж. Милларом, 1881, Чарльз Гриффин, Лондон.

[Partington_122-12] Партингтон, Дж. Р. (1949), Расширенный трактат по физической химии., 1, Основные принципы. Свойства газов, Лондон: Longmans, Green and Co., п. 122

[13] Максвелл, Дж. (1871), Теория тепла (первое изд.), Лондон: Longmans, Green and Co., п. 129

[14] Лидделл, Х., Скотт, Р. (1940). Греко-английский лексикон, Clarendon Press, Oxford UK.

[15] Рэнкин, У. Дж. МакКью. (1854 г.). «О геометрическом представлении расширяющего действия тепла и теории термодинамических двигателей». Proc. Рой. Soc. 144: 115–175. Разные научные статьи с. 339

[16] Рэнкин, У. Дж. МакКью. (1854 г.). «О геометрическом представлении расширяющего действия тепла и теории термодинамических двигателей». Proc. Рой. Soc. 144: 115–175. Разные научные статьи с. 341.

[17] Брайан, Г. (1907). Термодинамика. Вводный трактат, посвященный главным образом Первым принципам и их прямым приложениям. Лейпциг: Б. Г. Тойбнер.

[18] Родился М. (1949). «Естественная философия причины и случая». Лондон: Издательство Оксфордского университета. Цитировать журнал требует | журнал = (помощь)

[Bailyn_Ch_3-19] а ^б Байлын, М. (1994). "Глава 3". Обзор термодинамики. Нью-Йорк, штат Нью-Йорк: Американский институт физики. ISBN 0-88318-797-3.

[20] Родился М. (1927). «Физические аспекты квантовой механики». Природа. 119 (2992): 354–357. Bibcode:1927Натура.119..354Б. Дои:10.1038 / 119354a0. (Перевод Роберта Оппенгеймера.)

[21] «диабатический процесс». Американское метеорологическое общество. Получено 24 ноября 2020.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]