Ханойская башня - Tower of Hanoi



В Ханойская башня (также называемый Башня Брахмы или же Башня Лукаса[1] и иногда во множественном числе как Башни) это математическая игра или же головоломка. Он состоит из трех стержней и ряда дисков разного размера, которые могут надеваться на любую стержень. Головоломка начинается с дисков, собранных в аккуратную стопку в порядке возрастания размера на одном стержне, наименьшее наверху, таким образом получается конический форма.
Задача головоломки - переместить всю стопку на другой стержень, соблюдая следующие простые правила:
- Одновременно можно перемещать только один диск.
- Каждый ход состоит в том, чтобы взять верхний диск из одной из стопок и положить его поверх другой стопки или на пустой стержень.
- Диск большего размера нельзя ставить поверх диска меньшего размера.
С 3 дисками головоломку можно решить за 7 ходов. Минимальное количество ходов, необходимых для решения загадки Ханойской башни, - 2.п - 1, где п количество дисков.
Происхождение
Головоломка была изобретена Французский математик Эдуард Лукас в 1883 году. Практически сразу же возникли многочисленные мифы о древней и мистической природе головоломки.[2] Есть рассказ о Индийский храм в Каши Вишванатх в котором находится большая комната с тремя изношенными столбами, окруженная 64 золотыми дисками. Брамин С тех пор жрецы, выполняя приказ древнего пророчества, перемещали эти диски в соответствии с неизменными правилами Брахмы. Поэтому загадка также известна как Башня Брахма головоломка. Согласно легенде, когда будет завершен последний ход головоломки, наступит конец света.[3]
Если бы легенда была правдой и если бы священники могли перемещать диски со скоростью один в секунду, используя наименьшее количество ходов, им потребовалось бы 264 - 1 секунда или примерно 585 миллиард лет, чтобы закончить,[4] что примерно в 42 раза больше нынешнего возраста Вселенной.
Есть много вариаций этой легенды. Например, в некоторых рассказах храм - это монастырь, а священники монахи. Можно сказать, что храм или монастырь находятся в разных частях мира, включая Ханой, Вьетнам - и может быть связан с любым религия. В некоторых версиях представлены другие элементы, такие как тот факт, что башня была создана в начале мира, или что священники или монахи могут делать только один ход в день.
Решение
В головоломку можно играть с любым количеством дисков, хотя во многих версиях игрушек их от 7 до 9. Минимальное количество ходов, необходимых для решения загадки Ханойской башни, - 2.п - 1, где п количество дисков.[5] Это как раз то пth Число Мерсенна.
Итерационное решение

Простое решение для игрушечной головоломки - это чередовать ходы между самым маленьким и немалым кусочком. При перемещении самого маленького фрагмента всегда перемещайте его на следующую позицию в том же направлении (вправо, если начальное количество частей четное, влево, если начальное количество фигур нечетное). Если в выбранном направлении нет позиции башни, переместите фишку на противоположный конец, но затем продолжайте движение в правильном направлении. Например, если вы начали с трех частей, вы переместите самую маленькую часть на противоположный конец, а затем продолжите в левом направлении. Когда наступает очередь переместить не самую маленькую фигуру, возможен только один ход. Это завершит головоломку за наименьшее количество ходов.[6]
Более простая формулировка итеративного решения
Для четного количества дисков:
- сделать допустимый ход между колышками A и B (в любом направлении),
- сделать допустимое перемещение между колышками A и C (в любом направлении),
- сделать допустимый ход между колышками B и C (в любом направлении),
- повторять до завершения.
Для нечетного количества дисков:
- сделать допустимое перемещение между колышками A и C (в любом направлении),
- сделать допустимый ход между колышками A и B (в любом направлении),
- сделать допустимый ход между колышками B и C (в любом направлении),
- повторять до завершения.
В каждом случае всего 2п - Сделан 1 ход.
Эквивалентное итерационное решение
Другой способ сгенерировать уникальное оптимальное итеративное решение:
Пронумеруйте диски от 1 до п (от наибольшего к наименьшему).
- Если п нечетно, первый ход - от привязки A к привязке C.
- Если п четное, первый ход - от привязки A к привязке B.
Теперь добавьте эти ограничения:
- Нечетный диск нельзя размещать непосредственно на нечетном.
- Ни один четный диск не может быть помещен непосредственно на четный диск.
- Иногда возможны две привязки: на одной будут диски, а на другой - пусто. Установите диск на непустой колышек.
- Никогда не перемещайте диск дважды подряд.
Учитывая эти ограничения после первого хода, в каждый последующий ход возможен только один допустимый ход.
Последовательность этих уникальных ходов является оптимальным решением проблемы, эквивалентной итерационному решению, описанному выше.[7]
Рекурсивное решение
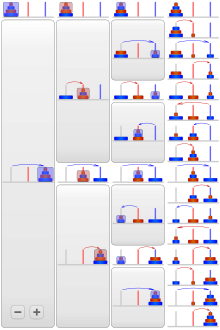
Ключом к рекурсивному решению проблемы является осознание того, что ее можно разбить на набор более мелких подзадач, для каждой из которых та же самая общая процедура решения, которую мы ищем применяется, и полное решение затем находится в некоторых просто путь от решений этих подзадач. Каждая из созданных таким образом подзадач «меньшего размера» гарантирует, что в конечном итоге будет достигнут базовый вариант (я). Оттуда для Ханойских башен:
- пометьте колышки A, B, C,
- позволять п общее количество дисков,
- пронумеруйте диски от 1 (самый маленький, самый верхний) до п (самый большой, самый нижний).
Предполагая, что все п диски распределяются между колышками в правильном порядке; предполагая, что есть м верхние диски на источник колышек, а все остальные диски больше, чем м, поэтому их можно спокойно игнорировать; двигаться м диски с привязки источника к цель привязать с помощью запасной колышек, не нарушая правил:
- Двигаться м - 1 диск из источник к запасной привязка, по та же общая процедура решения. Правила не нарушаются по предположениям. Это оставляет диск м как верхний диск на исходной привязке.
- Переместите диск м от источник к цель колышек, который гарантированно будет правильным ходом, исходя из предположений - простой шаг.
- Переместите м - 1 диск, который мы только что поместили в запасной, из запасной к цель привязать та же общая процедура решения, поэтому они размещаются сверху диска м не нарушая правил.
- Базовый вариант - переехать 0 диски (в шагах 1 и 3), то есть ничего не делают, что, очевидно, не нарушает правил.
Таким образом, полное решение Ханойской башни состоит из перемещения п диски от исходного стержня A к целевому стержню C, используя B в качестве резервного стержня.
Этот подход может быть подвергнут строгому математическому доказательству с помощью математическая индукция и часто используется как пример рекурсии при обучении программированию.
Логический анализ рекурсивного решения
Как и во многих математических головоломках, найти решение проще, если решить чуть более общую задачу: как переместить башню час (высота) диски от стартового колышка ж = А (из) на привязку назначения т = C (к), B оставшаяся третья привязка и предполагая т ≠ ж. Во-первых, заметьте, что проблема симметрична для перестановок имен колышков (симметричная группа S3 ). Если решение известно, переход от привязки А привязать C, затем, переименовав привязки, то же решение можно использовать для любого другого выбора начальной и конечной привязки. Если есть только один диск (или вообще нет), проблема тривиальна. Если час = 1, то просто переместите диск из колышка А привязать C. Если час > 1, то где-то в последовательности ходов нужно переместить самый большой диск из колышка А к другому стержню, желательно привязать C. Единственная ситуация, которая позволяет этот ход, - это когда все меньше час - 1 диск на колышке B. Следовательно, прежде всего час - 1 меньший диск должен выйти из А к B. Затем переместите самый большой диск и, наконец, переместите час - 1 меньший диск из колышка B привязать C. Наличие самого большого диска не мешает перемещению час - 1 диск меньшего размера и может быть временно проигнорирован. Теперь проблема сводится к переезду час - 1 диск с одного колышка на другой, сначала с А к B а затем из B к C, но оба раза можно использовать один и тот же метод, переименовав колышки. Эту же стратегию можно использовать для уменьшения час - 1 проблема на час − 2, час - 3 и так далее, пока не останется только один диск. Это называется рекурсией. Этот алгоритм можно схематически представить следующим образом.
Определите диски в порядке увеличения их размера натуральными числами от 0 до, но не включая час. Следовательно, диск 0 самый маленький, а диск час - 1 самый крупный.
Ниже приводится процедура перемещения башни из час диски из колышка А на колышек C, с B оставшаяся третья привязка:
- Если час > 1, затем сначала используйте эту процедуру, чтобы переместить час - 1 меньший диск из колышка А привязать B.
- Теперь самый большой диск, т.е. диск час можно сдвинуть с колышка А привязать C.
- Если час > 1, затем снова используйте эту процедуру, чтобы переместить час - 1 меньший диск из колышка B привязать C.
Посредством математическая индукция, легко доказывается, что описанная выше процедура требует минимально возможного числа ходов, и что полученное решение является единственным с таким минимальным количеством ходов. С помощью повторяющиеся отношения, точное количество ходов, необходимых для этого решения, можно рассчитать следующим образом: . Этот результат получается из того, что шаги 1 и 3 принимают движется, а шаг 2 занимает одно движение, давая .
Рекурсивная реализация
Следующее Python Код выделяет важную функцию рекурсивного решения, которую иначе можно неправильно понять или упустить. То есть на каждом уровне рекурсии первый рекурсивный вызов инвертирует цель и вспомогательный стеки, а во втором рекурсивном вызове источник и вспомогательный стеки перевернуты.
А = [3, 2, 1]B = []C = []def двигаться(п, источник, цель, вспомогательный): если п > 0: # Переместите n - 1 диск из источника во вспомогательный, чтобы они не мешали двигаться(п - 1, источник, вспомогательный, цель) # Перемещаем n-й диск из источника в цель цель.добавить(источник.поп()) # Показать наш прогресс Распечатать(А, B, C, '##############', сен=' п') # Переместите n - 1 диск, который мы оставили на вспомогательном устройстве, на целевой двигаться(п - 1, вспомогательный, цель, источник)# Инициируйте вызов от источника A к цели C с помощью вспомогательного Bдвигаться(3, А, C, B)Следующий код реализует больше рекурсивных функций для текстовой анимации:
импорт времяА = [я за я в классифицировать(5, 0, -1)]высота = len(А) - 1 # Стабильное значение высоты для анимацииB = []C = []def двигаться(п, источник, цель, вспомогательный): если п > 0: # Переместите n - 1 диск из источника во вспомогательный, чтобы они не мешали двигаться(п - 1, источник, вспомогательный, цель) # Перемещаем n-й диск из источника в цель цель.добавить(источник.поп()) # Отобразить наш прогресс, используя рекурсивную функцию, чтобы вывести его draw_disks(А, B, C, высота) Распечатать("") # Обеспечьте интервал время.спать(0.3) # Сделайте паузу, чтобы оживить # Переместите n - 1 диск, который мы оставили на вспомогательном устройстве, на целевой двигаться(п - 1, вспомогательный, цель, источник)def draw_disks(А, B, C, позиция, ширина=2 * int(Максимум(А))): # параметр ширины по умолчанию равен двойному размеру самого большого диска в начальной башне. если позиция >= 0: # Если A имеет значение в списке в данной позиции, создать диск в его позиции (высоте) valueInA = " " если позиция >= len(А) еще create_disk(А[позиция]) # То же самое для B и C valueInB = " " если позиция >= len(B) еще create_disk(B[позиция]) valueInC = " " если позиция >= len(C) еще create_disk(C[позиция]) # Распечатать каждую строку Распечатать("{0:^{ширина}}{1:^{ширина}}{2:^{ширина}}".формат(valueInA, valueInB, valueInC, ширина=ширина)) # Рекурсивно вызвать этот метод еще раз до следующей позиции (высоты) draw_disks(А, B, C, позиция - 1, ширина) еще: # Когда закончите с рекурсией, распечатать метки столбцов Распечатать("{0:^{ширина}}{1:^{ширина}}{2:^{ширина}}".формат("А", "B", "C", ширина=ширина))def create_disk(размер): "" "Простой рекурсивный метод создания наклонного диска." "" если размер == 1: возвращаться "/\\" еще: возвращаться "/" + create_disk(размер - 1) + "\\"# Инициируйте вызов от источника A к цели C с помощью вспомогательного Bдвигаться(len(А), А, C, B)Нерекурсивное решение
Составленный рекурсивным алгоритмом список перемещений башни с одного колышка на другой, имеет много закономерностей. При подсчете ходов, начиная с 1, порядковый номер диска, который будет перемещен во время хода м это количество раз м можно разделить на 2. Следовательно, каждый нечетный ход включает наименьший диск. Также можно заметить, что наименьший диск пересекает колышки. ж, т, р, ж, т, ри т.д. для нечетной высоты башни и пересекает колышки ж, р, т, ж, р, ти т.д. для равной высоты башни. Это обеспечивает следующий алгоритм, который проще выполнять вручную, чем рекурсивный алгоритм.
В альтернативных ходах:
- Переместите самый маленький диск на стержень, с которого он недавно не брался.
- Легально переместить другой диск (будет только одна возможность).
Для самого первого хода самый маленький диск устанавливается на колышек. т если час странно и привязано р если час даже.
Также обратите внимание, что:
- Диски, порядковые номера которых имеют четность, перемещаются в том же смысле, что и самый маленький диск.
- Диски, порядковые номера которых имеют нечетную четность, движутся в противоположном направлении.
- Если час четно, оставшаяся третья привязка во время последовательных ходов т, р, ж, т, р, ж, так далее.
- Если час нечетно, оставшаяся третья привязка во время последовательных ходов р, т, ж, р, т, ж, так далее.
Обладая этими знаниями, набор дисков в середине оптимального решения может быть восстановлен без дополнительной информации о состоянии, кроме позиций каждого диска:
- Назовите ходы, описанные выше, «естественным» ходом диска.
- Изучите самый маленький верхний диск, который не является диском 0, и отметьте, каким будет его единственный (законный) ход: если такого диска нет, то мы либо на первом, либо на последнем перемещении.
- Если это перемещение является «естественным» перемещением диска, то диск не перемещался с момента последнего перемещения диска 0, и это перемещение должно быть выполнено.
- Если это движение не является «естественным» движением диска, переместите диск 0.
Бинарное решение
Положение дисков может быть определено более непосредственно из двоичный (base-2) представление номера хода (начальное состояние - ход # 0, все цифры 0, а конечное состояние - все цифры 1), используя следующие правила:
- Есть одна двоичная цифра (кусочек ) для каждого диска.
- Самый старший (крайний левый) бит представляет собой самый большой диск. Значение 0 указывает, что самый большой диск находится на начальной привязке, а 1 указывает, что он находится на последней привязке (правая привязка, если количество дисков нечетное, и средняя привязка в противном случае).
- Строка битов читается слева направо, и каждый бит может использоваться для определения местоположения соответствующего диска.
- Бит с тем же значением, что и предыдущий, означает, что соответствующий диск размещен поверх предыдущего диска на той же привязке.
- (То есть: прямая последовательность единиц или нулей означает, что все соответствующие диски находятся на одной привязке.)
- Бит с другим значением по сравнению с предыдущим означает, что соответствующий диск находится на одну позицию слева или справа от предыдущего. Правильно оно или левое определяется этим правилом:
- Предположим, что начальный колышек находится слева.
- Также предположим "обертывание" - так что правый колышек считается как один колышек "левый" от левого колышка, и наоборот.
- Позволять п быть количеством больших дисков, которые расположены на той же привязке, что и их первый больший диск, и прибавить 1, если самый большой диск находится на левой привязке. Если п четный, диск расположен на один колышек вправо, если п нечетно, диск располагается на один колышек слева (в случае четного числа дисков и наоборот).
Например, в 8-дисковом Ханое:
- Переместите 0 = 00000000.
- Самый большой диск равен 0, поэтому он находится на левой (начальной) привязке.
- Все остальные диски тоже равны 0, поэтому они кладутся поверх него. Следовательно, все диски находятся на начальном штифте.
- Перемещение 28 − 1 = 11111111.
- Самый большой диск - 1, поэтому он находится на среднем (конечном) стержне.
- Все остальные диски тоже по 1, поэтому они ставятся на него стопкой. Следовательно, все диски находятся на последнем штифте, и загадка завершена.
- Двигаться 21610 = 11011000.
- Самый большой диск - 1, поэтому он находится на среднем (конечном) стержне.
- Второй диск тоже 1, поэтому он ставится на него сверху, на средний колышек.
- Третий диск равен 0, поэтому он находится на другом стержне. С п нечетный (п = 1), это один колышек слева, то есть на левом колышке.
- Четвертый диск равен 1, поэтому он находится на другом колышке. С п нечетный (п = 1), он находится на один колышек слева, то есть на правом колышке.
- Пятый диск тоже 1, поэтому он ставится на него, на правый колышек.
- Шестой диск равен 0, значит, он на другой привязке. С п даже (п = 2) диск находится на один колышек вправо, т.е. на левый колышек.
- Диски седьмой и восьмой тоже равны 0, поэтому они укладываются на него, на левый колышек.
Колышки источника и назначения для м-й ход также элегантно можно найти из двоичного представления м с помощью побитовые операции. Чтобы использовать синтаксис Язык программирования C, двигаться м из колышка (m & m - 1)% 3 привязать ((м | м - 1) + 1)% 3, где диски начинаются на привязке 0 и заканчиваются на привязке 1 или 2 в зависимости от того, четное или нечетное количество дисков. Другая формулировка взята из колышка (м - (м & -м))% 3 привязать (м + (м & -м))% 3.
Кроме того, диск, который нужно переместить, определяется количеством перемещений (м) можно разделить на 2 (т.е. количество нулевых битов справа), считая первый ход как 1 и идентифицируя диски числами 0, 1, 2 и т. д. в порядке увеличения размера. Это позволяет очень быстрой нерекурсивной компьютерной реализации находить положения дисков после m перемещений без ссылки на какое-либо предыдущее перемещение или распределение дисков.
Операция по подсчету количества последовательных нулей в конце двоичного числа дает простое решение проблемы: диски нумеруются с нуля, а при движении м, номер диска подсчитывать конечные нули перемещается на минимально возможное расстояние вправо (при необходимости возвращаясь влево).[8]
Решение с кодом Грея
Двоичная система счисления Коды Грея дает альтернативный способ решения головоломки. В системе Грея числа выражаются двоичной комбинацией нулей и единиц, а не стандартными. позиционная система счисления, Код Грея работает при условии, что каждое значение отличается от своего предшественника только на один (и ровно на один) измененный бит.
Если в коде Грея подсчитывается размер бита, равный количеству дисков в конкретной Ханойской башне, начинается с нуля и увеличивается, тогда бит, изменяемый при каждом перемещении, соответствует перемещаемому диску, где наименее значимый бит это самый маленький диск, а старший бит - самый большой.
- Подсчет ходов от 1 и идентификация дисков числами, начиная с 0 в порядке увеличения размера, порядковый номер диска, который будет перемещен во время перемещения м это количество раз м можно разделить на 2.
Этот метод определяет, какой диск переместить, но не определяет, куда его переместить. Для самого маленького диска всегда есть две возможности. Для других дисков всегда есть одна возможность, кроме случаев, когда все диски находятся на одной и той же привязке, но в этом случае либо это наименьший диск, который необходимо переместить, либо цель уже достигнута. К счастью, есть правило, которое говорит, куда переместить самый маленький диск. Позволять ж быть отправной точкой, т привязка назначения и р оставшийся третий колышек. Если количество дисков нечетное, наименьший диск проходит по колышкам в следующем порядке: ж → т → р → ж → т → ри т. д. Если количество дисков четное, это необходимо поменять местами: ж → р → т → ж → р → т, так далее.[9]
Положение смены бита в решении кода Грея дает размер диска, перемещаемого на каждом шаге: 1, 2, 1, 3, 1, 2, 1, 4, 1, 2, 1, 3, 1, 2, 1, ... (последовательность A001511 в OEIS ),[10] последовательность, также известная как функция линейки, или на единицу больше, чем степень двойки в числе ходов. в Язык Wolfram Language, IntegerExponent [Диапазон [2 ^ 8 - 1], 2] + 1 дает ходы для головоломки с 8 дисками.
Графическое представление
Игра может быть представлена неориентированный граф, узлы, представляющие распределения дисков и ребра, представляющие ходы. Для одного диска график представляет собой треугольник:

График для двух дисков представляет собой три треугольника, соединенных в углы большего треугольника.
Вторая буква добавляется для обозначения большего диска. Ясно, что изначально его нельзя переместить.
Самый верхний маленький треугольник теперь представляет одноходовые возможности с двумя дисками:

Узлы в вершинах крайнего треугольника представляют распределения со всеми дисками на одном стержне.
Для h + 1 дисков возьмите график из h дисков и замените каждый маленький треугольник графиком для двух дисков.
Для трех дисков график выглядит следующим образом:

- назовите колышки a, b и c
- перечислить позиции на диске слева направо в порядке увеличения размера
Стороны крайнего треугольника представляют собой кратчайшие пути перемещения башни с одного колышка на другой. Ребро в середине сторон самого большого треугольника представляет собой движение самого большого диска. Ребро в середине сторон каждого следующего меньшего треугольника представляет собой перемещение каждого следующего меньшего диска. Стороны самого маленького треугольника представляют собой движения самого маленького диска.

В общем, для пазла с п диски, есть 3п узлы в графе; каждый узел имеет три ребра по отношению к другим узлам, кроме трех угловых узлов, у которых их два: всегда можно переместить наименьший диск на один из двух других колышков, и можно переместить один диск между этими двумя колышками Кроме в ситуации, когда все диски уложены на одном колышке. Угловые узлы представляют три случая, когда все диски уложены на одном стержне. Диаграмма для п + 1 диск можно получить, взяв три копии п-дисковая диаграмма - каждая из них представляет все состояния и перемещения меньших дисков для одной конкретной позиции нового самого большого диска - и объединяет их по углам с тремя новыми краями, представляя единственные три возможности для перемещения самого большого диска. Таким образом, получившаяся фигура имеет 3п+1 узлов и по-прежнему имеет три угла и только два ребра.
По мере добавления дисков графическое представление игры будет напоминать фрактал фигура, Серпинский треугольник. Ясно, что подавляющее большинство позиций в головоломке никогда не будут достигнуты при использовании кратчайшего возможного решения; действительно, если жрецы легенды используют максимально долгое решение (без повторного посещения какой-либо позиции), им потребуется 364 - 1 ход или более 1023 годы.
Самый длинный неповторяющийся путь для трех дисков можно визуализировать, удалив неиспользуемые края:

Между прочим, этот самый длинный неповторяющийся путь можно получить, запретив все ходы из а к б.
В Гамильтонов цикл для трех дисков это:

Графики четко показывают, что:
- Из любого произвольного распределения дисков существует ровно один кратчайший способ переместить все диски на одну из трех опор.
- Между каждой парой произвольных распределений дисков существует один или два различных кратчайших пути.
- Из каждого произвольного распределения дисков существует один или два разных самых длинных несамопересекающихся пути для перемещения всех дисков на одну из трех опор.
- Между каждой парой произвольных распределений дисков есть один или два разных самых длинных несамопересекающихся пути.
- Позволять Nчас быть количеством несамопересекающихся путей для перемещения башни час диски с одного колышка на другой. Потом:
- N1 = 2
- Nчас+1 = (Nчас)2 + (Nчас)3
Это дает Nчас быть 2, 12, 1872, 6563711232, ... (последовательность A125295 в OEIS )
Вариации
Прилегающие колышки
Если все ходы должны быть между соседними колышками (т. Е. При данных колышках A, B, C нельзя перемещаться напрямую между колышками A и C), то перемещение стопки п дисков от штифта A к штифту C занимает 3п - 1 ход. В решении используются все 3п действительные позиции, всегда делая уникальный ход, который не отменяет предыдущий ход. Положение со всеми дисками на штифте B достигается на полпути, то есть после (3п - 1) / 2 хода.[нужна цитата ]
Циклический Ханой
В Cyclic Hanoi нам даются три колышка (A, B, C), которые расположены в виде круга, причем направления по часовой стрелке и против часовой стрелки определены как A - B - C - A и A - C - B - A соответственно. Направление движения диска должно быть по часовой стрелке.[11] Достаточно изобразить последовательность перемещаемых дисков. Решение можно найти с помощью двух взаимно рекурсивных процедур:
Двигаться п диски против часовой стрелки к соседнему целевому колышку:
- двигаться п - 1 диск против часовой стрелки к целевой привязке
- переместить диск #п один шаг по часовой стрелке
- двигаться п - 1 диск по часовой стрелке к стартовой привязке
- переместить диск #п один шаг по часовой стрелке
- двигаться п - 1 диск против часовой стрелки к целевой привязке
Двигаться п диски по часовой стрелке к соседнему целевому колышку:
- двигаться п - 1 диск против часовой стрелки на запасной колышек
- переместить диск #п один шаг по часовой стрелке
- двигаться п - 1 диск против часовой стрелки к целевой привязке
Пусть C (n) и A (n) представляют собой движущиеся n дисков по и против часовой стрелки, тогда мы можем записать обе формулы:
C (n) = A (n-1) n A (n-1) и A (n) = A (n-1) n C (n-1) n A (n-1).
Таким образом, C (1) = 1 и A (1) = 1 1, C (2) = 1 1 2 1 1 и A (2) = 1 1 2 1 2 1 1.
Решение для Cyclic Hanoi имеет несколько интересных свойств:
1) Схема перемещений при переносе башни дисков с колышка на другой колышек симметрична относительно центральных точек.
2) Самый маленький диск - это первый и последний диск, который нужно переместить.
3) Группы самых маленьких ходов диска чередуются с одиночными ходами других дисков.
4) Количество ходов дисков, заданное C (n) и A (n), минимально.
С четырьмя колышками и более
Хотя версия с тремя колышками имеет простое рекурсивное решение, давно известное, оптимальное решение проблемы Ханойской башни с четырьмя колышками (так называемая головоломка Рива) не было проверено Бушем до 2014 года.[12]
Однако в случае четырех или более привязок алгоритм Фрейма-Стюарта известен без доказательства оптимальности с 1941 года.[13]
Формальный вывод точного числа минимальных ходов, необходимых для решения задачи, с помощью алгоритма Фрейма – Стюарта (и других эквивалентных методов) см. В следующей статье.[14]
По поводу других вариантов задачи о Ханойской башне с четырьмя колышками см. Обзорную статью Пола Стокмейера.[15]
Алгоритм Фрейма – Стюарта
Алгоритм Фрейма-Стюарта описан ниже:
- Позволять быть количеством дисков.
- Позволять быть количеством колышков.
- Определять быть минимальным числом перемещений, необходимых для передачи n дисков с помощью r стержней.
Алгоритм можно описать рекурсивно:
- Для некоторых , , перенести верх диски к единственной привязке, кроме начальной или конечной, принимая движется.
- Не трогая колышек, на котором теперь находится верх диски, перенесите оставшиеся дисков к целевой привязке, используя только оставшиеся колышки, взяв движется.
- Наконец, перенесите верх диски на колышек назначения, взяв движется.
Весь процесс занимает движется. Следовательно, счет следует выбирать, для которого это количество минимально. В случае с 4 штифтами оптимальная равно , куда это ближайшая целочисленная функция.[16] Например, в курсе UPenn CIS 194 на Haskell первая страница задания[17] перечисляет оптимальное решение для случая с 15 дисками и 4 штифтами как 129 шагов, что получается для указанного выше значения k.
Предполагается, что этот алгоритм оптимален для любого количества привязок; его количество ходов 2Θ (п1/(р−2)) (для фиксированных р).
Общие кратчайшие пути и числа 466/885
Любопытное обобщение исходной цели головоломки состоит в том, чтобы начать с заданной конфигурации дисков, где все диски не обязательно находятся на одном стержне, и прийти за минимальное количество ходов в другую заданную конфигурацию. В общем, может быть довольно сложно вычислить кратчайшую последовательность ходов для решения этой проблемы. Решение было предложено Андреасом Хинцем и основано на наблюдении, что в кратчайшей последовательности перемещений нужно переместить самый большой диск (очевидно, можно игнорировать все самые большие диски, которые будут занимать одну и ту же точку в обоих начальных и окончательные конфигурации) переместятся либо ровно один раз, либо ровно дважды.
Математика, связанная с этой обобщенной проблемой, становится еще более интересной, если учесть средний количество ходов в кратчайшей последовательности ходов между двумя начальными и конечными конфигурациями диска, выбранными случайным образом. Хинц и Чан Тат-Хунг независимо друг от друга открыли[18][19] (смотрите также[20]:Глава 1, с. 14), что среднее количество ходов в башне из n дисков определяется следующей точной формулой:
Для достаточно больших п, только первое и второе слагаемые не сходятся к нулю, поэтому мы получаем асимптотическое выражение: , в качестве . Таким образом, интуитивно мы могли интерпретировать долю как представление соотношения усилий, которые необходимо выполнить при переходе от случайно выбранной конфигурации к другой случайно выбранной конфигурации, относительно сложности перехода «наиболее трудного» пути длины который включает в себя перемещение всех дисков с одного стержня на другой. Альтернативное объяснение появления константы 466/885, а также новый и несколько улучшенный алгоритм вычисления кратчайшего пути дал Ромик.[21]
Магнитный Ханой
В Magnetic Tower of Hanoi каждый диск имеет две различные стороны, северную и южную (обычно окрашены в красный и синий цвета). Диски нельзя ставить одинаковыми полюсами вместе - магниты на каждом диске предотвращают это незаконное движение. диск необходимо переворачивать при перемещении.

Двухцветные башни Ханоя
Этот вариант знаменитой головоломки Ханойская башня предлагался учащимся 3–6 классов 2ème Championnat de France des Jeux Mathématiques et Logiques состоялась в июле 1988 г.[22]

Правила головоломки по сути те же: диски передаются между колышками по одному. Ни в коем случае нельзя ставить больший диск поверх меньшего. Разница в том, что теперь для каждого размера есть два диска: черный и белый. Кроме того, теперь есть две башни дисков чередующихся цветов. Цель головоломки - сделать башни одноцветными (одного цвета). Предполагается, что самые большие диски в нижней части башен поменяются местами.
Ханойская башня
Разновидность головоломки была адаптирована как пасьянс с девятью игральными картами под названием Ханойская башня.[23][24] Неизвестно, намеренно или случайно изменено написание исходного названия.[25]
Приложения
Ханойская башня часто используется в психологических исследованиях решение проблем. Также существует вариант этой задачи под названием Башня Лондона для нейропсихологической диагностики и лечения исполнительных функций.
Чжан и Норман[27] использовали несколько изоморфных (эквивалентных) представлений игры для изучения влияния репрезентативного эффекта на дизайн задач. Они продемонстрировали влияние на производительность пользователей, изменив способ представления правил игры, используя вариации в физическом дизайне компонентов игры. Эти знания повлияли на разработку фреймворка TURF.[28] для представления взаимодействие человека с компьютером.
Ханойская башня также используется как схема ротации резервных копий при выполнении компьютерных данных резервные копии где задействовано несколько лент / носителей.
Как упоминалось выше, Ханойская башня популярна для обучения рекурсивным алгоритмам начинающих программистов. Наглядная версия этой головоломки запрограммирована в emacs редактор, доступ к которому можно получить, набрав M-x hanoi. Также существует образец алгоритма, написанный на Пролог.
Ханойская башня также используется нейропсихологами в качестве теста для оценки лобная доля дефицит.[29]
В 2010 году исследователи опубликовали результаты эксперимента, который показал, что вид муравьев Линепитема униженная смогли успешно решить 3-дисковую версию проблемы Ханойской башни с помощью нелинейной динамики и сигналов феромонов.[30]
In 2014, scientists synthesized multilayered palladium nanosheets with a Tower of Hanoi like structure.[26]
В популярной культуре
In the science fiction story "Now Inhale", by Eric Frank Russell,[31] a human is held prisoner on a planet where the local custom is to make the prisoner play a game until it is won or lost before his execution. The protagonist knows that a rescue ship might take a year or more to arrive, so he chooses to play Towers of Hanoi with 64 disks. (This story makes reference to the legend about the Buddhist monks playing the game until the end of the world.)
In the 1966 Доктор Кто история The Celestial Toymaker, то одноименный villain forces the Doctor to play a ten-piece 1,023-move Tower of Hanoi game entitled The Trilogic Game with the pieces forming a pyramid shape when stacked.
In 2007, the concept of the Towers Of Hanoi problem was used in Professor Layton and the Diabolical Box in puzzles 6, 83, and 84, but the disks had been changed to pancakes. The puzzle was based around a dilemma where the chef of a restaurant had to move a pile of pancakes from one plate to the other with the basic principles of the original puzzle (i.e. three plates that the pancakes could be moved onto, not being able to put a larger pancake onto a smaller one, etc.)
В фильме Rise of the Planet of the Apes (2011), this puzzle, called in the film the "Lucas Tower", is used as a test to study the intelligence of apes.
The puzzle is featured regularly in приключение и головоломка игры. Since it is easy to implement, and easily recognised, it is well-suited to use as a puzzle in a larger graphical game (e.g. Звездные войны: Рыцари Старой Республики и Массовый эффект ).[32] Some implementations use straight disks, but others disguise the puzzle in some other form. There is an arcade version by Sega.[33]
A 15-disk version of the puzzle appears in the game Sunless Sea as a lock to a tomb. The player has the option to click through each move of the puzzle in order to solve it, but the game notes that it will take 32767 moves to complete. If an especially dedicated player does click through to the end of the puzzle, it is revealed that completing the puzzle does not unlock the door.
В Yu-Gi-Oh! VRAINS, a hacking group called "Knight of Hanoi" create a structure named "Tower of Hanoi" within the eponymous VRAINS virtual reality network.
This was first used as a challenge in survivor Thailand in 2002 but rather than rings, the pieces were made to resemble a temple. Sook Jai threw the challenge to get rid of Jed even though Shii-Ann knew full well how to complete the puzzle.The problem is featured as part of a reward challenge in a 2011 episode of the American version of the Оставшийся в живых Сериал. Both players (Ozzy Lusth и Benjamin "Coach" Wade ) struggled to understand how to solve the puzzle and are aided by their fellow tribe members.
Смотрите также
| Часть серии по |
| Puzzles |
|---|
 |
Примечания
- ^ Hofstadter, Douglas R. (1985). Metamagical Themas : Questing for the Essence of Mind and Pattern. New York: Basic Books. ISBN 978-0-465-04540-2.
- ^ Hinz, Andreas M.; Klavžar, Sandi; Milutinović, Uroš; Petr, Ciril (2013-01-31). The Tower of Hanoi – Myths and Maths. ISBN 978-3034802369.
- ^ Spitznagel, Edward L. (1971). Selected topics in mathematics. Holt, Rinehart and Winston. п.137. ISBN 978-0-03-084693-9.
- ^ Moscovich, Ivan (2001). 1000 playthinks: puzzles, paradoxes, illusions & games. Workman. ISBN 978-0-7611-1826-8.
- ^ Petković, Miodrag (2009). Famous Puzzles of Great Mathematicians. AMS Bookstore. п. 197. ISBN 978-0-8218-4814-2.
- ^ Troshkin, M. "Doomsday Comes: A Nonrecursive Analysis of the Recursive Towers-of-Hanoi Problem". Фокус (на русском). 95 (2): 10–14.
- ^ Mayer, Herbert; Perkins, Don (1984). "Towers of Hanoi Revisited". SIGPLAN Notices. 19 (2): 80–84. Дои:10.1145/948566.948573. S2CID 2304761.
- ^ Warren, Henry S. (2003). "Section 5-4: Counting Trailing 0's.". Hacker's delight (1-е изд.). Boston MA: Addison-Wesley. ISBN 978-0-201-91465-8.
- ^ Miller, Charles D. (2000). "Ch. 4: Binary Numbers and the Standard Gray Code". Mathematical Ideas (9 ed.). Addison Wesley Longman. ISBN 978-0-321-07607-6. Archived from the original on 2004-08-21.CS1 maint: BOT: статус исходного URL-адреса неизвестен (связь)
- ^ Gros, L. (1872). Théorie du Baguenodier. Lyon: Aimé Vingtrinier.
- ^ Gedeon, T. D. (1996). "The Cyclic Towers of Hanoi: An Iterative Solution Produced by Transformation". The Computer Journal. 39 (4): 353–356. Дои:10.1093/comjnl/39.4.353.
- ^ Bousch, T. (2014). "La quatrieme tour de Hanoi" (PDF). Бык. Belg. Математика. Soc. Simon Stevin. 21: 895–912. Дои:10.36045/bbms/1420071861. S2CID 14243013.
- ^ Stewart, B. M.; Frame, J. S. (March 1941). "Solution to advanced problem 3819". American Mathematical Monthly. 48 (3): 216–9. Дои:10.2307/2304268. JSTOR 2304268.
- ^ Klavzar, Sandi; Milutinovi, Uro; Petrb, Ciril (2002). "Variations on the Four-Post Tower of Hanoi Puzzle" (Postscript). Congressus Numerantium. 102.
- ^ Stockmeyer, Paul (1994). "Variations on the Four-Post Tower of Hanoi Puzzle" (Postscript). Congressus Numerantium. 102: 3–12.
- ^ "University of Toronto CSC148 Slog". 5 апреля 2014 г.. Получено 22 июля, 2015.
- ^ "UPenn CIS 194 Introduction to Haskell Assignment 1" (PDF). Получено 31 января, 2016.
- ^ Hinz, A. (1989). "The Tower of Hanoi". L'Enseignement Mathématique. 35: 289–321. Дои:10.5169/seals-57378.
- ^ Chan, T. (1988). "A statistical analysis of the towers of Hanoi problem". Internat. J. Comput. Математика. 28 (1–4): 57–65. Дои:10.1080/00207168908803728.
- ^ Stewart, Ian (2004). Another Fine Math You've Got Me Into... Courier Dover. ISBN 978-0-7167-2342-4.
- ^ Romik, D. (2006). "Shortest paths in the Tower of Hanoi graph and finite automata". SIAM Journal on Discrete Mathematics. 20 (3): 610–622. arXiv:math/0310109. Дои:10.1137/050628660. S2CID 8342396.
- ^ Prasad Vithal Chaugule (2015). "A Recursive Solution to Bicolor Towers of Hanoi Problem" (PDF). Recreational Mathematics Magazine (4): 37–48. ISSN 2182-1976.
- ^ Arnold, Peter (2003-05-28). Card Games for One. Sterling Publishing Company. ISBN 978-0-600-60727-4.
- ^ Hedges, Sid G. (2018-03-06). Everybody's Book of Hobbies. Read Books Ltd. ISBN 978-1-5287-8344-6.
- ^ "Tower Of Hanoy Patience (AKA Tower Of Hanoi Patience)". bbcmicro.co.uk. Получено 2020-10-17.
- ^ а б Yin, Xi; Liu, Xinhong; Pan, Yung-Tin; Walsh, Kathleen A.; Yang, Hong (November 4, 2014). "Hanoi Tower-like Multilayered Ultrathin Palladium Nanosheets". Nano Letters. 14 (12): 7188–94. Bibcode:2014NanoL..14.7188Y. Дои:10.1021/nl503879a. PMID 25369350.
- ^ Zhang, J (1994). "Representations in distributed cognitive tasks" (PDF). Cognitive Science. 18: 87–122. Дои:10.1016/0364-0213(94)90021-3.
- ^ Zhang, Jiajie; Walji, Muhammad F. (2011). "TURF: Toward a unified framework of EHR usability". Journal of Biomedical Informatics. 44 (6): 1056–67. Дои:10.1016/j.jbi.2011.08.005. PMID 21867774.
- ^ Beers, S. R.; Rosenberg, D. R.; Dick, E. L.; Williams, T.; O'Hearn, K. M.; Birmaher, B.; Ryan, C. M. (1999). "Neuropsychological study of frontal lobe function in psychotropic-naive children with obsessive-compulsive disorder". The American Journal of Psychiatry. 156 (5): 777–9. Дои:10.1176/ajp.156.5.777 (inactive 2020-12-05). PMID 10327915.CS1 maint: DOI inactive as of December 2020 (связь)
- ^ Reid, C.R.; Sumpter, D.J.; Beekman, M. (January 2011). "Optimisation in a natural system: Argentine ants solve the Towers of Hanoi". J. Exp. Biol. 214 (Pt 1): 50–8. CiteSeerX 10.1.1.231.9201. Дои:10.1242/jeb.048173. PMID 21147968. S2CID 18819977.
- ^ Russell, Eric Frank (April 1959). "Now Inhale". Поразительная научная фантастика.
- ^ "Tower of Hanoi (video game concept)". Giantbomb.com. Получено 2010-12-05.
- ^ "Tower of Hanoi / Andamiro". Sega Amusements. Архивировано из оригинал on 2012-03-01. Получено 2012-02-26.




















