Сюръективная функция - Surjective function

В математика, а функция ж из набор Икс к набору Y является сюръективный (также известен как на, или сюрприз), если для каждого элемент у в codomain Y из ж, есть хотя бы один элемент Икс в домен Икс из ж такой, что ж(Икс) = у.^[1]^[2]^[3] Не требуется, чтобы Икс быть уникальный; функция ж может отображать один или несколько элементов Икс к тому же элементу Y.

Сюръективная функция из домен Икс к codomain Y. Функция сюръективна, потому что каждый элемент в кодомене является значением ж(Икс) хотя бы для одного элемента Икс в домене.

Период, термин сюръективный и связанные термины инъективный и биективный были представлены Николя Бурбаки,^[4]^[5] группа в основном Французский 20 век математики который под этим псевдонимом написал серию книг, представляющих изложение современной высшей математики, начиная с 1935 года. Французское слово сюр средства над или же над, и связано с тем, что изображение области определения сюръективной функции полностью покрывает область определения функции.

Любая функция индуцирует сюръекцию ограничение его кодомен к образу его домена. Каждая сюръективная функция имеет правый обратный, и каждая функция с правым обратным обязательно является сюръекцией. В сочинение сюръективных функций всегда сюръективно. Любую функцию можно разложить на сюръекцию и инъекцию.

Определение

А сюръективная функция это функция чей изображение равен своему codomain. Эквивалентно функция ${displaystyle f}$ с домен ${displaystyle X}$ и codomain ${displaystyle Y}$ сюръективно, если для каждого ${displaystyle y}$ в ${displaystyle Y}$ существует хотя бы один ${displaystyle x}$ в ${displaystyle X}$ с ${displaystyle f (x) = y}$ .^[2] Сюрприз иногда обозначают двуглавой стрелкой вправо (U + 21A0 ↠ ДВЕ СТРЕЛКА ВПРАВО),^[6] как в ${displaystyle fcolon X woheadrightarrow Y}$ .

Символично,

Если

{displaystyle fcolon Xightarrow Y}

, тогда

{displaystyle f}

называется сюръективным, если

{displaystyle forall yin Y ,, существует xin X, ;; f (x) = y}

.^[3]^[7]

Примеры

Несюръективная функция из домен Икс к codomain Y. Меньший желтый овал внутри Y это изображение (также называемый классифицировать ) из ж. Эта функция нет сюръективный, потому что изображение не заполняет весь кодомен. Другими словами, Y раскрашивается в два этапа: во-первых, для каждого Икс в Икс, смысл ж(Икс) окрашена в желтый цвет; Во-вторых, все остальные точки в Y, которые не являются желтыми, окрашены в синий цвет. Функция ж был бы сюръективным, только если бы не было синих точек.

Для любого набора Икс, то функция идентичности я бы_Икс на Икс сюръективно.
Функция ж : Z → {0,1} определяется ж(п) = п мод 2 (то есть четное целые числа отображаются в 0 и странный целых до 1) сюръективно.
Функция ж : р → р определяется ж(Икс) = 2Икс +1 сюръективен (и даже биективный ), потому что для каждого настоящий номер у, у нас есть Икс такой, что ж(Икс) = у: такой подходящий Икс является (у − 1)/2.
Функция ж : р → р определяется ж(Икс) = Икс³ − 3Икс сюръективно, потому что прообраз любого настоящий номер у - множество решений кубического полиномиального уравнения Икс³ − 3Икс − у = 0, и каждый кубический многочлен с действительными коэффициентами имеет хотя бы один действительный корень. Однако эта функция не инъективный (и, следовательно, не биективный ), поскольку, например, прообраз у = 2 равно {Икс = −1, Икс = 2}. (Фактически, прообраз этой функции для каждого у, −2 ≤ у ≤ 2 имеет более одного элемента.)
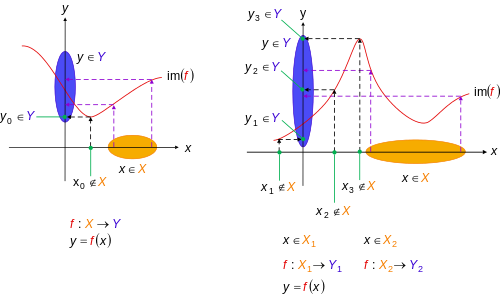
Функция грамм : р → р определяется грамм(Икс) = Икс² является нет сюръективный, поскольку нет действительного числа Икс такой, что Икс² = −1. Однако функция грамм : р → р₀⁺ определяется грамм(Икс) = Икс² (с ограниченным кодоменом) является сюръективно, поскольку для каждого у в неотрицательной реальной области Y, есть хотя бы один Икс в реальной области Икс такой, что Икс² = у.
В натуральный логарифм функция ln: (0, + ∞) → р является сюръективным и даже биективным (отображение множества положительных действительных чисел на множество всех действительных чисел). Его обратное, экспоненциальная функция, если он определен с набором действительных чисел в качестве домена, не является сюръективным (поскольку его диапазон - это набор положительных действительных чисел).
В матричная экспонента не сюръективен, когда рассматривается как карта из пространства всех п×п матрицы себе. Однако обычно ее определяют как карту из пространства всех п×п матрицы к общая линейная группа степени п (то есть группа из всех п×п обратимые матрицы ). Согласно этому определению, матричная экспонента сюръективна для комплексных матриц, но все же не сюръективна для реальных матриц.
В проекция из декартово произведение А × B к одному из его факторов сюръективно, если другой фактор не пуст.
В трехмерной видеоигре векторы проецируются на плоский двумерный экран с помощью сюръективной функции.

Интерпретация для сюръективные функции в декартовой плоскости, определяемой отображением ж : Икс → Y, куда у = ж(Икс), Икс = область действия, Y = диапазон функции. Каждый элемент в диапазоне отображается на элемент в домене по правилу ж. Может быть несколько элементов домена, которые соответствуют одному и тому же элементу диапазона. То есть каждый у в Y отображается из элемента Икс в Икс, больше одного Икс можно сопоставить с тем же у. Оставили: Показан только один домен, который делает ж сюръективный. Правильно: два возможных домена Икс₁ и Икс₂ показаны.

Несюръективные функции в декартовой плоскости. Хотя некоторые части функции сюръективны, где элементы у в Y имеют ценность Икс в Икс такой, что у = ж(Икс), некоторые части нет. Оставили: Есть у₀ в Y, но нет Икс₀ в Икс такой, что у₀ = ж(Икс₀). Правильно: Есть у₁, у₂ и у₃ в Y, но нет Икс₁, Икс₂, и Икс₃ в Икс такой, что у₁ = ж(Икс₁), у₂ = ж(Икс₂), и у₃ = ж(Икс₃).

Характеристики

Функция биективный тогда и только тогда, когда он одновременно сюръективен и инъективный.

Если (как это часто бывает) функция отождествляется с ее график, то сюръективность - это не свойство самой функции, а скорее свойство отображение.^[8] Это функция вместе с ее содоменом. В отличие от инъективности, сюръективность не может быть прочитана только по графику функции.

Сюрприз как правые обратимые функции

Функция грамм : Y → Икс считается правый обратный функции ж : Икс → Y если ж(грамм(у)) = у для каждого у в Y (грамм может быть отменено ж). Другими словами, грамм это правая инверсия ж если сочинение ж о грамм из грамм и ж в таком порядке функция идентичности на домене Y из грамм. Функция грамм не обязательно быть полным обратный из ж потому что композиция в другом порядке, грамм о ж, может не быть функцией идентификации в домене Икс из ж. Другими словами, ж можно отменить или "обеспечить регресс" грамм, но не может быть отменен им.

Каждая функция с правым обратным обязательно является сюръекцией. Утверждение, что каждая сюръективная функция имеет правый обратный, эквивалентно аксиома выбора.

Если ж : Икс → Y сюръективно и B это подмножество из Y, тогда ж(ж⁻¹(B)) = B. Таким образом, B можно восстановить из прообраз ж⁻¹(B).

Например, на первой иллюстрации выше есть функция грамм такой, что грамм(C) = 4. Еще есть функция ж такой, что ж(4) = C. Неважно, что грамм(C) также может равняться 3; имеет значение только то, что ж "переворачивает" грамм.

Сюръективная композиция: первая функция не обязательно должна быть сюръективной.
Еще одна сюръективная функция. (Это случайно биекция )
А не-сюръективная функция. (Это случайно инъекция )

Сюрпризы как эпиморфизмы

Функция ж : Икс → Y сюръективен тогда и только тогда, когда он право-отменяющий:^[9] учитывая любые функции грамм,час : Y → Z, в любое время грамм о ж = час о ж, тогда грамм = час. Это свойство сформулировано в терминах функций и их сочинение и может быть обобщен на более общее понятие морфизмы из категория и их состав. Право-сокращательные морфизмы называются эпиморфизмы. В частности, сюръективные функции - это в точности эпиморфизмы в категория наборов. Префикс эпи происходит от греческого предлога ἐπί смысл над, над, на.

Любой морфизм с правым обратным является эпиморфизмом, но в общем случае обратное неверно. Правый обратный грамм морфизма ж называется раздел из ж. Морфизм с правым обратным называется расщепленный эпиморфизм.

Сюрпризы как бинарные отношения

Любая функция с доменом Икс и codomain Y можно рассматривать как левый итог и право-уникальный бинарная связь между Икс и Y отождествляя его с его график функции. Сюръективная функция с областью определения Икс и codomain Y тогда является бинарным отношением между Икс и Y которая уникальна справа и как полная слева, так и правильный итог.

Мощность области сюръекции

В мощность области определения сюръективной функции больше или равно мощности ее области значений: если ж : Икс → Y является сюръективной функцией, то Икс имеет как минимум столько же элементов, сколько Y, в смысле Количественные числительные. (Доказательство обращается к аксиома выбора чтобы показать, что функцияграмм : Y → Икс удовлетворение ж(грамм(у)) = у для всех у в Y существуют. грамм легко видеть инъективным, поэтому формальное определение из |Y| ≤ |Икс| доволен.)

В частности, если оба Икс и Y находятся конечный с таким же количеством элементов, то ж : Икс → Y сюръективно тогда и только тогда, когда ж является инъективный.

Учитывая два набора Икс и Y, обозначение Икс ≤^* Y используется, чтобы сказать, что либо Икс пусто или что есть сюрприз от Y на Икс. Используя аксиому выбора, можно показать, что Икс ≤^* Y и Y ≤^* Икс вместе подразумевают, что |Y| = |Икс|, вариант Теорема Шредера – Бернштейна..

Состав и разложение

В сочинение сюръективных функций всегда сюръективно: если ж и грамм оба сюръективны, и область грамм совпадает с областью ж, тогда ж о грамм сюръективно. Наоборот, если ж о грамм сюръективно, то ж сюръективно (но грамм, функция, примененная первой, не обязательно). Эти свойства обобщаются из сюрпризов в категория наборов любому эпиморфизмы в любом категория.

Любую функцию можно разложить на сюръекцию и инъекция: Для любой функции час : Икс → Z есть сюрприз ж : Икс → Y и укол грамм : Y → Z такой, что час = грамм о ж. Чтобы увидеть это, определите Y быть набором прообразы час⁻¹(z) куда z в час(Икс). Эти прообразы непересекающийся и раздел Икс. потом ж несет каждый Икс к элементу Y который его содержит, и грамм несет каждый элемент Y в точку в Z которому час отправляет свои очки. потом ж сюръективно, так как это отображение проекции, и грамм инъективен по определению.

Индуцированная сюръекция и индуцированная биекция

Любая функция вызывает сюръекцию, ограничивая свой домен своим диапазоном. Любая сюръективная функция индуцирует биекцию, определенную на частное области его области путем свертывания всех сопоставлений аргументов с заданным фиксированным изображением. Точнее, каждое сюрприз ж : А → B может быть факторизован как проекция с последующей биекцией следующим образом. Позволять А/ ~ быть классы эквивалентности из А под следующими отношение эквивалентности: Икс ~ у если и только если ж(Икс) = ж(у). Эквивалентно, А/ ~ - множество всех прообразов под ж. Позволять п(~) : А → А/ ~ быть карта проекции который отправляет каждый Икс в А своему классу эквивалентности [Икс]_~, и разреши ж_п : А/~ → B - корректно определенная функция, задаваемая ж_п([Икс]_~) = ж(Икс). потом ж = ж_п о п(~).

Смотрите также

дальнейшее чтение

Бурбаки, Н. (2004) [1968]. Теория множеств. Элементы математики. 1. Springer. Дои:10.1007/978-3-642-59309-3. ISBN 978-3-540-22525-6. LCCN 2004110815.

[1] "Окончательный словарь высшего математического жаргона - Онто". Математическое хранилище. 2019-08-01. Получено 2019-12-07.

[:0-2] а ^б «Инъективный, сюръективный и биективный». www.mathsisfun.com. Получено 2019-12-07.

[:1-3] а ^б "Биекция, инъекция и сюрприз | Блестящая вики по математике и науке". brilliant.org. Получено 2019-12-07.

[4] Миллер, Джефф, «Инъекция, сюръекция и взаимная инъекция», Самые ранние случаи использования некоторых слов математики, Штатив.

[5] Машааль, Морис (2006). Бурбаки. American Mathematical Soc. п. 106. ISBN 978-0-8218-3967-6.

[Unicode_Arrows-6] «Стрелки - Юникод» (PDF). Получено 2013-05-11.

[7] Фарлоу, С. Дж. «Уколы, уколы и инъекции» (PDF). math.umaine.edu. Получено 2019-12-06.

[8] Апостол Т.М. (1981). Математический анализ. Эддисон-Уэсли. п. 35.

[9] Голдблатт, Роберт (2006) [1984]. Топои, категориальный анализ логики (Пересмотренная ред.). Dover Publications. ISBN 978-0-486-45026-1. Получено 2009-11-25.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]