Теория структурной инженерии - Structural engineering theory

Рисунок болт в срезать. Верхний рисунок иллюстрирует одинарный сдвиг, нижний рисунок - двойной сдвиг.

Строительная инженерия зависит от детального знания грузы, физика и материалы чтобы понять и спрогнозировать, как конструкции выдерживают и выдерживают собственный вес и приложенные нагрузки. Для успешного применения знаний инженерам-строителям потребуется детальное знание математика и соответствующих эмпирических и теоретических кодексов проектирования. Им также нужно будет знать о коррозия сопротивление материалов и конструкций, особенно когда эти конструкции подвергаются воздействию внешней среды.

Критериями, определяющими проектирование конструкции, являются либо эксплуатационная пригодность (критерии, которые определяют, способна ли конструкция адекватно выполнять свою функцию), либо прочность (критерии, которые определяют, способна ли конструкция безопасно поддерживать и противостоять расчетным нагрузкам). Инженер-строитель проектирует конструкцию так, чтобы сила и жесткость чтобы соответствовать этим критериям.

Нагрузки на конструкции поддерживаются силами, передаваемыми через элементы конструкции. Эти силы могут проявляться как напряжение (осевая сила), сжатие (осевая сила), срезать, и изгиб, или же изгиб (изгибающий момент - это сила, умноженная на расстояние или плечо рычага, что создает эффект поворота или крутящий момент ).

Сила

Сила зависит от свойств материала. Прочность материала зависит от его способности выдерживать осевое стресс, напряжение сдвига, изгиб и кручение. Прочность материала измеряется в силе на единицу площади (ньютоны на квадратный миллиметр или Н / мм², или эквивалентные мегапаскали или МПа в системе СИ и часто фунты на квадратный дюйм в системе обычных единиц США).

Конструкция не соответствует критерию прочности, когда стресс (сила, разделенная на площадь материала), вызванная нагрузкой, превышает способность конструкционного материала выдерживать нагрузку без разрушения, или когда напряжение (процентное расширение) настолько велико, что элемент больше не выполняет свою функцию (урожай ).

Смотрите также:

Смотрите также: Предел прочности, Прочность на сжатие, и Прочность на сдвиг

Жесткость

Жесткость зависит от свойств материала и геометрия. Жесткость конструктивного элемента из данного материала - это произведение материала Модуль для младших и элемент второй момент площади. Жесткость измеряется в силе на единицу длины (ньютонов на миллиметр или Н / мм) и эквивалентна «силовой постоянной» в Закон Гука.

В отклонение конструкции под нагрузкой зависит от ее жесткости. В динамический ответ конструкции к динамическим нагрузкам ( собственная частота конструкции) также зависит от ее жесткости.

В конструкции, состоящей из нескольких структурных элементов, где поверхность, распределяющая силы между элементами, является жесткой, элементы будут нести нагрузки, пропорциональные их относительной жесткости - чем жестче элемент, тем большую нагрузку он будет воспринимать. Это означает, что соотношение нагрузка / жесткость, которое является прогибом, остается неизменным в двух соединенных (сочлененных) элементах. В конструкции, в которой поверхность, распределяющая силы между элементами, является гибкой (например, конструкция с деревянным каркасом), элементы будут нести нагрузки пропорционально их относительной площади притока.

Считается, что конструкция не соответствует выбранным критериям эксплуатационной пригодности, если она недостаточно жесткая, чтобы иметь приемлемо малые размеры. отклонение или же динамичный ответ под нагрузкой.

Обратное значение жесткости равно гибкость.

Смотрите также: Метод гибкости и Метод прямой жесткости

Факторы безопасности

Безопасное проектирование конструкций требует подхода к проектированию, учитывающего статистический вероятность выхода конструкции из строя. Нормы проектирования конструкций основаны на предположении, что как нагрузки, так и прочность материала изменяются в зависимости от нормальное распределение.^{[нужна цитата ]}

Работа инженера-строителя состоит в том, чтобы гарантировать, что вероятность перекрытия между распределением нагрузок на конструкцию и распределением прочности материала конструкции является приемлемо малой (свести этот шанс к нулю невозможно).

Это нормально применять частичный коэффициент безопасности к нагрузкам и прочности материала, при проектировании с использованием 95-го процентиля (два Стандартное отклонение от иметь в виду ). Коэффициент запаса прочности, применяемый к нагрузке, обычно гарантирует, что в 95% случаев фактическая нагрузка будет меньше расчетной, в то время как коэффициент, применяемый к прочности, гарантирует, что в 95% раз фактическая прочность будет выше расчетной. .

Коэффициенты запаса прочности материала различаются в зависимости от материала и области его применения, а также от проектных норм, применяемых в стране или регионе.

Более сложный подход к моделированию структурной безопасности - полагаться на структурная надежность, в котором нагрузки и сопротивления моделируются как вероятностные переменные.^[1][2] Однако использование этого подхода требует детального моделирования распределения нагрузок и сопротивлений. Кроме того, его вычисления требуют больших вычислений.

Варианты нагрузки

А случай нагрузки представляет собой комбинацию различных типов нагрузок с примененными к ним запасами прочности. Конструкция проверяется на прочность и пригодность к эксплуатации при всех нагрузках, которые могут возникнуть в течение ее срока службы.

Типичные загружения для расчета прочности (предельные нагрузки; ULS):

1,2 х собственная нагрузка + 1,6 х динамическая нагрузка

1,2 x собственная нагрузка + 1,2 x действующая нагрузка + 1,2 x ветровая нагрузка

Типичный вариант нагружения для расчета эксплуатационной пригодности (характерные нагружения; SLS):

1,0 x собственная нагрузка + 1,0 x динамическая нагрузка

Для разных условий нагрузки будут использоваться разные загружения. Например, в случае пожарной конструкции вариант нагрузки 1,0 x собственная нагрузка + 0,8 x действующая нагрузка могут быть использованы, поскольку разумно предположить, что все покинули здание в случае пожара.

В многоэтажных зданиях нормально снижать общую временную нагрузку в зависимости от количества поддерживаемых этажей, поскольку вероятность приложения максимальной нагрузки ко всем этажам одновременно пренебрежимо мала.

Для больших зданий нередко требуется учитывать при проектировании сотни различных нагрузок.

Законы движения Ньютона

Основная статья: Законы движения Ньютона

Наиболее важные естественные законы для строительной инженерии: Законы движения Ньютона

Первый закон Ньютона гласит, что каждое тело остается в состоянии покоя или равномерного движения вперед, за исключением тех случаев, когда оно вынуждено изменить свое состояние под воздействием силы.

Второй закон Ньютона гласит, что скорость изменения количества движения тела пропорциональна результирующей силе, действующей на тело, и имеет то же направление. Математически F = ma (сила = масса x ускорение).

Третий закон Ньютона гласит, что все силы действуют парами, и эти две силы равны по величине и противоположны по направлению.

С помощью этих законов можно понять силы, действующие на структуру, и то, как эта структура будет им сопротивляться. Третий закон требует, чтобы конструкция была устойчивой, все внутренние и внешние силы должны быть внутри. равновесие. Это означает, что сумма всех внутренних и внешних сил на диаграмма свободного тела должно быть равно нулю:

• ${\displaystyle \sum {\vec {F}}=0}$: векторная сумма силы действие на тело равно нулю. Это означает

Σ ЧАС = 0: сумма горизонтальных составляющих сил равна нулю;

Σ V = 0: сумма вертикальных составляющих сил равна нулю;

• ${\displaystyle \sum {\vec {M}}=0}$: сумма моменты (около произвольной точки) всех сил равняется нулю.

Статическая определенность

Основная статья: Статически неопределенный

Инженер-строитель должен понимать внутренние и внешние силы структурной системы, состоящей из структурных элементов и узлов на их пересечении.

Статически детерминированная структура может быть полностью проанализирована, используя только рассмотрение равновесия, исходя из законов движения Ньютона.

Статически неопределенная структура имеет больше неизвестных, чем из соображений равновесия можно получить уравнения для (см. одновременные уравнения ). Такую систему можно решить, рассматривая уравнения совместимость между геометрией и прогибами в дополнение к уравнениям равновесия, или с помощью виртуальная работа.

Если система состоит из ${\displaystyle b}$ бары ${\displaystyle j}$ шарнирные соединения и ${\displaystyle r}$ опорных реакций, то его нельзя определить статически, если не соблюдаются следующие соотношения:

${\displaystyle r+b=2j}$

Даже если это соотношение действительно сохраняется, структура может быть устроена таким образом, чтобы быть статически неопределимой.^[3]

Эластичность

Основная статья: Эластичность

Смотрите также: Закон Гука

Многие инженерные разработки основаны на предположении, что материалы обладают упругими свойствами. Для большинства материалов это предположение неверно, но эмпирические данные показали, что проектирование с использованием этого предположения может быть безопасным. Упругие материалы подчиняются закону Гука, и пластичность не возникает.

Для систем, которые подчиняются закону Гука, производимое расширение прямо пропорционально нагрузке:

${\displaystyle {\vec {\mathbf {F} }}=k{\vec {\mathbf {x} }}\ }$

куда

Икс это расстояние, на которое пружина была растянута или сжата от положения равновесия, то есть положения, в котором пружина естественным образом остановится [обычно в метрах],

F это восстанавливающая сила, проявляемая материалом [обычно в ньютонах], и

k это силовая постоянная (или же жесткость пружины). Это жесткость весны. Константа имеет единицы силы на единицу длины (обычно в ньютоны на метр )

Пластичность

Сравнение критериев Трески и фон Мизеса

Основная статья: Пластичность

Некоторые конструкции основаны на предположении, что материалы будут вести себя пластически.^[4] Пластичный материал - это материал, который не подчиняется закону Гука, и поэтому деформация не пропорциональна приложенной нагрузке. Пластиковые материалы пластичный материалы. Теория пластичности может использоваться для некоторых железобетонных конструкций, предполагая, что они недостаточно армированы, что означает, что стальная арматура разрушается раньше, чем бетон.

Теория пластичности утверждает, что точка, в которой конструкция разрушается (достигает текучести), находится между верхней и нижней границей нагрузки, определяемой следующим образом:

• Если для данной внешней нагрузки можно найти распределение моментов, удовлетворяющее требованиям равновесия, с моментом, не превышающим момент текучести в любом месте, и если выполняются граничные условия, то данная нагрузка является нижняя граница на разрушение нагрузки.
• Если для небольшого приращения смещения внутренняя работа, выполняемая конструкцией, при условии, что момент на каждом пластическом шарнире равен моменту текучести и что граничные условия выполняются, равна внешней работе, совершаемой данной нагрузкой для то же самое небольшое приращение смещения, то эта нагрузка верхняя граница на разрушение нагрузки.

Если найдена правильная нагрузка на обрушение, оба метода дадут одинаковый результат для нагрузки обрушения.^[5]

Теория пластичности зависит от правильного понимания того, когда произойдет пластичность. Ряд различных моделей распределения напряжений и приближений к поверхность текучести из пластиковых материалов существуют:^[6]

• Круг Мора
• Критерий текучести фон Мизеса
• Анри Треска

Уравнение Эйлера-Бернулли для пучка

Прогиб консоли под точечной нагрузкой (f) в технике

Основная статья: Уравнение Эйлера-Бернулли для пучка

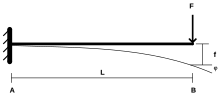
Уравнение Эйлера-Бернулли определяет поведение элемента балки (см. Ниже). Он основан на пяти предположениях:

1. Механика сплошной среды действительно для изгибаемой балки.
2. В стресс в поперечное сечение изменяется линейно в направлении изгиба и равна нулю на центроид каждого поперечное сечение.
3. Изгиб момент в конкретном поперечном сечении изменяется линейно со второй производной отклоненной формы в этом месте.
4. Балка состоит из изотропного материала.
5. Приложенная нагрузка ортогональна нейтральной оси балки и действует в уникальной плоскости.

Упрощенная версия уравнения Эйлера-Бернулли:

${\displaystyle {\frac {d^{2}}{dx^{2}}}\left(EI{\frac {d^{2}w}{dx^{2}}}\right)=q(x).\,}$

Здесь ${\displaystyle w}$ прогиб и ${\displaystyle q(x)}$ нагрузка на единицу длины. ${\displaystyle E}$ это модуль упругости и ${\displaystyle I}$ это второй момент площади, продукт этих жесткость на изгиб балки.

Это уравнение очень распространено в инженерной практике: оно описывает прогиб однородной статической балки.

Последовательные производные от ${\displaystyle w}$ имеют важное значение:

• ${\displaystyle \textstyle {w}\,}$ прогиб.

• ${\displaystyle \textstyle {\frac {dw}{dx}}\,}$ наклон балки.

• ${\displaystyle \textstyle {-EI{\frac {d^{2}w}{dx^{2}}}}\,}$ это изгибающий момент в луче.

• ${\displaystyle \textstyle {-{\frac {d}{dx}}\left(EI{\frac {d^{2}w}{dx^{2}}}\right)}\,}$ это сдвигающая сила в луче.

Изгибающий момент проявляется как сила растяжения и сила сжатия, действующие как пара в пучке. Напряжения, вызванные этими силами, могут быть представлены:

${\displaystyle \sigma ={\frac {My}{I}}=-Ey{\frac {d^{2}w}{dx^{2}}}\,}$

куда ${\displaystyle \sigma }$ это стресс, ${\displaystyle M}$ это изгибающий момент, ${\displaystyle y}$ это расстояние от нейтральная ось балки до рассматриваемой точки и ${\displaystyle I}$ это второй момент площади. Часто уравнение упрощается до момента, деленного на модуль сечения ${\displaystyle S}$, который ${\displaystyle I/y}$. Это уравнение позволяет инженеру-строителю оценить напряжение в элементе конструкции при воздействии изгибающего момента.

Коробление

Основная статья: Коробление

Столб под центрической осевой нагрузкой, демонстрирующий характерную деформацию коробления.

Под действием сжимающих сил элементы конструкции могут значительно деформироваться из-за дестабилизирующего воздействия этой нагрузки. Эффект может быть инициирован или усилен из-за возможных неточностей при изготовлении или конструкции.

Формула Эйлера определяет силу осевого сжатия, которая вызывает стойка (или столбец) не изгибается.

${\displaystyle F={\frac {\pi ^{2}EI}{(Kl)^{2}}}}$

куда

${\displaystyle F}$ = максимальный или критический сила (вертикальная нагрузка на колонну),

${\displaystyle E}$ = модуль упругости,

${\displaystyle I}$ = момент инерции площади, или второй момент площади

${\displaystyle l}$ = неподдерживаемая длина столбца,

${\displaystyle K}$ = коэффициент полезной длины колонны, значение которого зависит от условий концевой опоры колонны следующим образом.

На обоих концах шарнирные (шарнирные, свободно вращающиеся), ${\displaystyle K}$ = 1.0.

Для обоих концов зафиксировано, ${\displaystyle K}$ = 0.50.

Один конец закреплен, а другой закреплен штифтом, ${\displaystyle K\approx }$ 0.70.

Один конец зафиксирован, а другой конец свободно перемещается в боковом направлении, ${\displaystyle K}$ = 2.0.

Это значение иногда выражается для целей проектирования как критическая потеря устойчивости. стресс.

${\displaystyle \sigma ={\frac {\pi ^{2}E}{({\frac {Kl}{r}})^{2}}}}$

куда

${\displaystyle \sigma }$ = максимальный или критический стресс

${\displaystyle r}$ = наименьшее радиус вращения поперечного сечения

Другие формы продольного изгиба включают поперечный изгиб при кручении, когда сжатый фланец балки при изгибе будет изгибаться, и изгиб пластинчатых элементов в плоских балках из-за сжатия в плоскости пластины.

Смотрите также

• Структурный анализ
• Программное обеспечение для проектирования конструкций

Рекомендации

1. Мелчерз, Р. Э. (2002), «Анализ и прогнозирование структурной надежности», 2-е изд., Джон Вили, Чичестер, Великобритания..
2. Пирьонеси, Сайед Мадех; Таваколан, Мехди (9 января 2017 г.). «Модель математического программирования для решения задач оптимизации затрат и безопасности (CSO) при техническом обслуживании конструкций». KSCE Журнал гражданского строительства. 21 (6): 2226–2234. Дои:10.1007 / s12205-017-0531-z.
3. Дим, Клайв Л. (1997). Структурное моделирование и анализ. Издательство Кембриджского университета. п. 98. ISBN  0-521-49536-9.
4. Хейман, Жак (1998). Структурный анализ: исторический подход. Издательство Кембриджского университета. ISBN  0-521-62249-2.
5. Нильсон, Артур Х .; Дарвин, Дэвид; Долан, Чарльз В. (2004). Проектирование бетонных конструкций. McGraw-Hill Professional. п. 486. ISBN  0-07-248305-9.
6. Хейман, Жак (1999). Наука структурной инженерии. Imperial College Press. ISBN  1-86094-189-3.

• Кастильяно, Карло Альберто (переводчик: Эндрюс, Эварт С.) (1966). Теория равновесия упругих систем и ее приложения.. Dover Publications.
• Дим, Клайв Л. (1997). Структурное моделирование и анализ. Издательство Кембриджского университета. ISBN  0-521-49536-9.
• Дугас, Рене (1988). История механики. Courier Dover Publications. ISBN  0-486-65632-2.
• Хьюсон, Найджел Р. (2003). Предварительно напряженные бетонные мосты: проектирование и строительство. Томас Телфорд. ISBN  0-7277-2774-5.
• Хейман, Жак (1998). Структурный анализ: исторический подход. Издательство Кембриджского университета. ISBN  0-521-62249-2.
• Хейман, Жак (1999). Наука структурной инженерии. Imperial College Press. ISBN  1-86094-189-3.
• Хогнестад, Э. Исследование комбинированных изгибающих и осевых нагрузок в железобетонных элементах. Университет Иллинойса, Техническая экспериментальная станция, серия бюллетеней № 399.
• Дженнингс, Алан (2004) Структуры: от теории к практике. Тейлор и Фрэнсис. ISBN  978-0-415-26843-1.
• Леонхардт, А. (1964). Vom Caementum zum Spannbeton, Band III (от цемента до предварительно напряженного бетона). Bauverlag GmbH.
• МакНил, Ричард Х. (1994). Конечные элементы: их конструкция и характеристики. Марсель Деккер. ISBN  0-8247-9162-2.
• Мёрш Э. (Штутгарт, 1908). Der Eisenbetonbau, seine Theorie und Anwendung, (Железобетонная конструкция, ее теория и применение). Конрад Виттвер, 3-е издание.
• Nedwell, P.J .; Свами, Р.Н. (редактор) (1994). Ферроцемент: Материалы пятого международного симпозиума. Тейлор и Фрэнсис. ISBN  0-419-19700-1.
• Ньютон, Исаак; Лесер, Томас; Жакье, Франсуа (1822). Philosophiæ Naturalis Principia Mathematica. Оксфордский университет.
• Нильсон, Артур Х .; Дарвин, Дэвид; Долан, Чарльз В. (2004). Проектирование бетонных конструкций. McGraw-Hill Professional. ISBN  0-07-248305-9.
• Рожанская, Мариам; Левинова И. С. (1996). «Статика» в Morelon, Régis & Rashed, Roshdi (1996). Энциклопедия истории арабской науки, т. 2-3, Рутледж. ISBN  0-415-02063-8
• Schlaich, J., K. Schäfer, M. Jennewein (1987). "На пути к согласованному проектированию конструкционного бетона ". Журнал PCI, Специальный отчет, Том. 32, № 3.
• Скотт, Ричард (2001). По следам Такомы: подвесные мосты и поиски аэродинамической устойчивости. Публикации ASCE. ISBN  0-7844-0542-5.
• Тернер, Дж .; Clough, R.W .; Martin, H.C .; Топп, Л.Дж. (1956). «Жесткость и прогиб сложных конструкций». Журнал авиационной науки Выпуск 23.
• Вирди, К. (2000). Аномальные нагрузки на конструкции: экспериментальное и численное моделирование. Тейлор и Фрэнсис. ISBN  0-419-25960-0.