Коробление - Buckling

Для использования в других целях см. Buckling (значения).

Не путать с пряжка.

Кожаные вставки с пряжками на В-52 самолет. Панели из тонкой обшивки изгибаются при очень низких нагрузках. В показанном здесь случае вес передней конструкции фюзеляжа перед носовой частью шасси достаточен, чтобы вызвать прогиб панелей. Панели с пряжками по-прежнему эффективны в переносе сдвига при диагональном растяжении.^[1]

В Строительная инженерия, коробление это внезапное изменение формы (деформация ) из структурный компонент под нагрузка, например, поклон столбец под сжатие или сморщивание тарелки под срезать. Если конструкция подвергается постепенно возрастающей нагрузке, когда нагрузка достигает критического уровня, элемент может внезапно изменить форму, и говорят, что конструкция и компонент имеют пряжка.^[2] Критическая нагрузка Эйлера и Параболическая формула Джонсона используются для определения напряжения продольного изгиба в тонких колоннах.

Изгибание может произойти, даже если подчеркивает которые развиваются в структуре, намного ниже тех, которые необходимы, чтобы вызвать отказ в материале, из которого состоит конструкция. Дальнейшая нагрузка может вызвать значительные и несколько непредсказуемые деформации, что может привести к полной потере несущей способности элемента. Однако, если деформации, возникающие после изгиба, не вызывают полного разрушения этого элемента, элемент будет продолжать поддерживать нагрузку, вызвавшую его изгиб. Если изогнутый элемент является частью более крупного комплекса компонентов, такого как здание, любая нагрузка, приложенная к изогнутой части конструкции, сверх той, которая вызвала изгибание элемента, будет перераспределена внутри конструкции. Некоторые самолеты сконструированы для тонких панелей обшивки, чтобы продолжать нести нагрузку даже в изогнутом состоянии.

Формы коробления

Столбцы

Колонна под действием концентрической осевой нагрузки с характерной деформацией коробления.

Эксцентриситет осевой силы приводит к изгибающему моменту, действующему на балочный элемент.

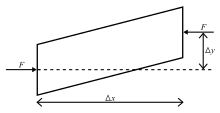
Отношение эффективной длины столбец в последнюю очередь радиус вращения его поперечного сечения называется коэффициент стройности (иногда обозначается греческой буквой лямбда, λ). Это соотношение дает возможность классифицировать колонны и их режимы отказа. Коэффициент гибкости важен с точки зрения дизайна. Все следующие значения являются приблизительными, используемыми для удобства.

Если нагрузка на колонну приложена через центр гравитации (центроид) его поперечного сечения, он называется осевой нагрузка. Нагрузка в любой другой точке поперечного сечения известна как эксцентричный нагрузка. Короткая колонна под действием осевой нагрузки выйдет из строя в результате прямого сжатия до того, как она прогнется, но длинная колонна, нагруженная таким же образом, выйдет из строя, внезапно отскочив наружу в боковом направлении (изгиб) в режиме изгиба. Режим прогиба с изгибом считается режимом разрушения и обычно возникает до того, как осевые сжимающие напряжения (прямое сжатие) могут вызвать разрушение материала из-за податливости или разрушения этого сжимающего элемента. Однако колонны средней длины выйдут из строя из-за сочетания прямого сжимающего напряжения и изгиба.

Особенно:

• Короткое стали столбец - тот, коэффициент гибкости которого не превышает 50; Стальная колонна промежуточной длины имеет коэффициент гибкости в диапазоне от примерно 50 до 200, и ее поведение определяется пределом прочности материала, в то время как длинная стальная колонна может иметь коэффициент гибкости более 200, и ее поведение является определяющим. по модулю упругости материала.
• Короткое конкретный Столбец - это столбец, имеющий отношение длины без опоры к наименьшему размеру поперечного сечения, равное или меньшее 10. Если отношение больше 10, оно считается длинным столбцом (иногда называемым тонким столбцом).
• Древесина Колонны могут быть классифицированы как короткие колонны, если отношение длины к наименьшему размеру поперечного сечения равно или меньше 10. Граница между колоннами из промежуточной и длинной древесины не может быть легко оценена. Один из способов определения нижнего предела длинных деревянных колонн состоит в том, чтобы установить его как наименьшее значение отношения длины к наименьшей площади поперечного сечения, которое просто превышает определенную константу K материала. Поскольку K зависит от модуль упругости и допустимое сжатие стресс параллельно волокну видно, что этот произвольный предел будет изменяться в зависимости от разновидность из древесины. Значение K указано в большинстве структурных справочников.

Теорию поведения колонн исследовал в 1757 году математик Леонард Эйлер. Он вывел формулу, формулу Эйлера, которая дает максимальную осевую нагрузку, которую длинная, тонкая, идеальная колонна может нести без потери устойчивости. Идеальная колонна - это колонна, которая идеально прямая, сделана из однородного материала и не подвержена начальным напряжениям. Когда приложенная нагрузка достигает нагрузки Эйлера, иногда называемой критической нагрузкой, колонна переходит в состояние нестабильности. равновесие. При такой нагрузке приложение малейшей поперечной силы вызовет отказ колонны из-за внезапного «прыжка» в новую конфигурацию, и говорят, что колонна изогнулась. Это то, что происходит, когда человек стоит на пустой алюминиевой банке, а затем кратковременно постукивает по сторонам, в результате чего она мгновенно раздавливается (вертикальные стороны банки можно понимать как бесконечную серию чрезвычайно тонких столбцов).^{[нужна цитата ]} Формула, полученная Эйлером для длинных тонких столбцов, приведена ниже.

${\displaystyle F={\frac {\pi ^{2}EI}{(KL)^{2}}}}$

Чтобы получить математическую демонстрацию, прочтите: Критическая нагрузка Эйлера

куда

${\displaystyle F}$, максимальный или критический сила (вертикальная нагрузка на колонну),

${\displaystyle E}$, модуль упругости,

${\displaystyle I}$, самый маленький момент инерции площади (второй момент площади) поперечного сечения колонны,

${\displaystyle L}$, неподдерживаемая длина столбца,

${\displaystyle K}$, коэффициент эффективной длины колонны, значение которого зависит от условий торцевой опоры колонны следующим образом.

На обоих концах шарнирные (шарнирные, свободно вращающиеся), ${\displaystyle K=1.0}$.

Для обоих концов зафиксировано, ${\displaystyle K=0.50}$.

Один конец закреплен, а другой закреплен штифтом, ${\displaystyle K={\sqrt {2}}/2\approx 0.7071}$.

Один конец зафиксирован, а другой конец свободно перемещается в боковом направлении, ${\displaystyle K=2.0}$.

${\displaystyle KL}$ - эффективная длина колонны.

Изучение этой формулы позволяет выявить следующие факты, касающиеся несущей способности тонких колонн.

• В эластичность материала колонны, а не сжимающего прочность материала длины колонны определяет нагрузку на изгиб колонны.
• Изгибающая нагрузка напрямую пропорциональный к второй момент площади поперечного сечения.
• Граничные условия оказывают значительное влияние на критическую нагрузку тонких колонн. Граничные условия определяют режим изгиба колонны и расстояние между точками перегиба на кривой смещения отклоненной колонны. Точки перегиба в форме прогиба колонны - это точки, в которых кривизна колонны меняет знак, а также точки, в которых внутренние изгибающие моменты колонны равны нулю. Чем ближе точки перегиба, тем больше результирующая осевая нагрузка (противодействие) колонны.

Демонстрационная модель, иллюстрирующая различные формы потери устойчивости "Эйлера". Модель показывает, как граничные условия влияют на критическую нагрузку тонкой колонны. Обратите внимание, что столбцы идентичны, за исключением граничных условий.

Вывод из вышеизложенного состоит в том, что нагрузку на продольный изгиб колонны можно увеличить, изменив ее материал на материал с более высоким модулем упругости (E) или изменив конструкцию поперечного сечения колонны, чтобы увеличить ее момент инерции. Последнее можно сделать без увеличения веса колонны, распределив материал как можно дальше от главной оси поперечного сечения колонны. Для большинства целей наиболее эффективным материалом колонны является материал трубчатой ​​секции.

Другой вывод, который можно почерпнуть из этого уравнения, - это влияние длины на критическую нагрузку. Увеличение длины колонны без опоры вдвое снижает допустимую нагрузку. Сдерживание, обеспечиваемое концевыми соединениями колонны, также влияет на ее критическую нагрузку. Если соединения абсолютно жесткие (не позволяют вращать его концы), критическая нагрузка будет в четыре раза больше, чем для аналогичной колонны, концы которой закреплены (позволяя вращение ее концов).

Поскольку радиус инерции определяется как квадратный корень из отношения момента инерции колонны относительно оси к площади ее поперечного сечения, приведенная выше формула Эйлера может быть переформатирована путем замены радиуса инерции ${\displaystyle Ar^{2}}$ за ${\displaystyle I}$:

${\displaystyle \sigma ={\frac {F}{A}}={\frac {\pi ^{2}E}{(l/r)^{2}}}}$

куда ${\displaystyle \sigma =F/A}$ напряжение, вызывающее изгиб колонны, и ${\displaystyle l/r}$ коэффициент стройности.

Поскольку несущие колонны обычно имеют промежуточную длину, формула Эйлера практически не применима для обычного проектирования. Проблемы, которые вызывают отклонения от чистого поведения колонны Эйлера, включают несовершенство геометрии колонны в сочетании с пластичностью / нелинейным напряжением и деформацией материала колонны. Следовательно, был разработан ряд формул для эмпирических столбцов, которые согласуются с данными испытаний, и все они отражают коэффициент гибкости. Из-за неопределенности в поведении колонн для расчета подходящих факторы безопасности вводятся в эти формулы. Одна из таких формул - Формула Перри Робертсона который оценивает критическую нагрузку потери устойчивости на основе предполагаемой малой начальной кривизны, следовательно, эксцентриситета осевой нагрузки. Формула Ренкина Гордона (названа в честь Уильям Джон Маккорн Ренкин и Perry Hugesworth Gordon (1899-1966)) также основан на экспериментальных результатах и ​​предполагает, что колонна изгибается при нагрузке F_{Максимум} предоставлено:

${\displaystyle {\frac {1}{F_{\max }}}={\frac {1}{F_{e}}}+{\frac {1}{F_{c}}}}$

куда ${\displaystyle F_{e}}$ - максимальная нагрузка Эйлера и ${\displaystyle F_{c}}$ максимальная сжимающая нагрузка. Эта формула обычно дает консервативную оценку ${\displaystyle F_{\max }}$.

Самопогибание

Чтобы получить математическую демонстрацию, прочтите: Самопогибание

Отдельно стоящая вертикальная колонна с плотностью ${\displaystyle \rho }$, Модуль для младших ${\displaystyle E}$, а площадь поперечного сечения ${\displaystyle A}$, будет прогибаться под собственным весом, если его высота превышает определенное критическое значение:^[3][4][5]

${\displaystyle h_{\text{crit}}=\left({\frac {9B^{2}}{4}}\,{\frac {EI}{\rho gA}}\right)^{\frac {1}{3}}}$

куда ${\displaystyle g}$ ускорение свободного падения, ${\displaystyle I}$ это второй момент площади поперечного сечения балки, и ${\displaystyle B}$ это первый ноль Функция Бесселя первого вида порядка −1/3, что равно 1,86635086…

Изгиб пластин

А пластина представляет собой трехмерную структуру, ширина которой сопоставима с ее длиной, а толщина очень мала по сравнению с двумя другими ее размерами. Подобно колоннам, тонкие пластины испытывают деформацию продольного изгиба вне плоскости при воздействии критических нагрузок; однако, в отличие от изгиба колонн, плиты под действием изгибающих нагрузок могут продолжать нести нагрузки, называемые местным изгибом. Это явление невероятно полезно во многих системах, так как позволяет проектировать системы для обеспечения большей грузоподъемности.

Для прямоугольной пластины, поддерживаемой вдоль каждого края и нагруженной однородной сжимающей силой на единицу длины, полученное основное уравнение может быть выражено следующим образом:^[6]

${\displaystyle {\frac {\partial ^{4}w}{\partial x^{4}}}+2{\frac {\partial ^{4}w}{\partial x^{2}\partial y^{2}}}+{\frac {\partial ^{4}w}{\partial y^{4}}}={\frac {12\left(1-\nu ^{2}\right)}{Et^{3}}}\left(-N_{x}{\frac {\partial ^{2}w}{\partial x^{2}}}\right)}$

куда

${\displaystyle w}$отклонение от плоскости

${\displaystyle N_{x}}$, равномерно распределенная сжимающая нагрузка

${\displaystyle \nu }$, Коэффициент Пуассона

${\displaystyle E}$, модуль упругости

${\displaystyle t}$, толщина

Решение отклонения может быть разложено на две показанные гармонические функции:^[6]

${\displaystyle w=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }w_{mn}\sin \left({\frac {m\pi x}{a}}\right)\sin \left({\frac {n\pi y}{b}}\right)}$

куда

${\displaystyle m}$, количество полусинусоидальных искривлений, возникающих вдоль

${\displaystyle n}$, количество полусинусоидальных искривлений, возникающих по ширине

${\displaystyle a}$, длина образца

${\displaystyle b}$, ширина образца

Предыдущее уравнение можно подставить в предыдущее дифференциальное уравнение, где ${\displaystyle n}$ равно 1. ${\displaystyle N_{x}}$ можно разделить, предоставив уравнение для критической сжимающей нагрузки пластины:^[6]

${\displaystyle N_{x,cr}=k_{cr}{\frac {\pi ^{2}Et^{3}}{12\left(1-\nu ^{2}\right)b^{2}}}}$

куда

${\displaystyle k_{cr}}$, коэффициент потери устойчивости, определяемый по формуле:^[6]

${\displaystyle k_{cr}=\left({\frac {mb}{a}}+{\frac {a}{mb}}\right)^{2}}$

Коэффициент потери устойчивости зависит от вида образца, ${\displaystyle a}$ / ${\displaystyle {b}}$, а также количество продольных изгибов. Для увеличивающегося числа таких кривизны соотношение сторон обеспечивает изменяющийся коэффициент потери устойчивости; но каждое отношение дает минимальное значение для каждого ${\displaystyle m}$. Это минимальное значение затем можно использовать как постоянное, независимо от соотношения сторон изображения и ${\displaystyle m}$.^[6]

Учитывая, что напряжение определяется нагрузкой на единицу площади, для критического напряжения находится следующее выражение:

${\displaystyle \sigma _{cr}=k_{cr}{\frac {\pi ^{2}E}{12\left(1-\nu ^{2}\right)\left({\frac {b}{t}}\right)^{2}}}}$

Из полученных уравнений можно увидеть близкое сходство между критическим напряжением для колонны и для плиты. По ширине ${\displaystyle b}$ при усадке пластина действует больше как колонна, поскольку увеличивает сопротивление короблению по ширине пластины. Увеличение ${\displaystyle a}$ позволяет увеличить количество синусоидальных волн, создаваемых продольным изгибом, но также увеличивает сопротивление продольному изгибу по ширине.^[6] Благодаря этому пластина предпочитает изгибаться таким образом, чтобы количество изгибов было одинаковым как по ширине, так и по длине. Из-за граничных условий, когда плита нагружена критическим напряжением и изгибается, края, перпендикулярные нагрузке, не могут деформироваться вне плоскости и, следовательно, будут продолжать нести напряжения. Это создает неоднородную сжимающую нагрузку по концам, где напряжения действуют на половину эффективной ширины с обеих сторон образца, определяемую следующим образом:^[6]

${\displaystyle {\frac {b_{\text{eff}}}{b}}\approx {\sqrt {{\frac {\sigma _{cr}}{\sigma _{y}}}\left(1-1.022{\sqrt {\frac {\sigma _{cr}}{\sigma _{y}}}}\right)}}}$

куда

${\displaystyle b_{\text{eff}}}$, полезная ширина

${\displaystyle \sigma _{y}}$, давая напряжение

По мере увеличения нагруженного напряжения эффективная ширина продолжает уменьшаться; если напряжения на концах когда-либо достигнут предела текучести, пластина выйдет из строя. Это то, что позволяет изогнутой конструкции продолжать выдерживать нагрузки. Когда осевая нагрузка, превышающая критическую, отображается в зависимости от смещения, отображается основной путь. Демонстрирует сходство плиты с колонной при изгибе; однако после потери устойчивости основной путь раздваивается на вторичный путь, который изгибается вверх, обеспечивая возможность подвергаться более высоким нагрузкам, превышающим критическую нагрузку.

Изгиб-крутильный изгиб

Изгиб-скручивание можно описать как комбинацию реакции элемента на изгиб и скручивание при сжатии. Такой режим отклонения необходимо учитывать при проектировании. В основном это происходит в колоннах с «открытыми» поперечными сечениями и, следовательно, имеющих низкую жесткость на кручение, таких как каналы, конструкционные тройники, формы с двойным углом и одноугольные с равными опорами. Круглые поперечные сечения не испытывают такой формы потери устойчивости.

Боковое продольное изгибание

Продольный изгиб двутавра с вертикальной силой в центре: а) продольный вид, б) поперечное сечение возле опоры, в) поперечное сечение в центре с поперечно-крутильным изгибом

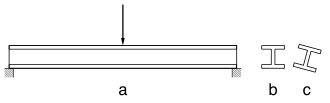
Когда балка без опоры загружается в изгиб, верхняя сторона в сжатие, а нижняя сторона - в напряжение. Если балка не поддерживается в боковом направлении (т. Е. Перпендикулярно плоскости изгиба), а изгибная нагрузка возрастает до критического предела, балка будет испытывать боковое отклонение сжатой полки, поскольку она локально изгибается. Боковое отклонение сжатой полки ограничивается стенкой балки и натяжной полкой, но для открытого участка режим скручивания более гибкий, поэтому балка как скручивается, так и отклоняется в сторону в режиме отказа, известном как продольный изгиб. В широкополочных профилях (с высокой жесткостью на боковой изгиб) режим прогиба будет в основном скрученным при кручении. В секциях с узкими полками жесткость на изгиб ниже, а прогиб колонны будет ближе к таковому в режиме поперечного изгиба.

Использование закрытых участков, например, квадратного полый профиль смягчат эффекты продольного изгиба при кручении за счет их высокой крутильная жесткость.

C_б коэффициент модификации, используемый в уравнении для номинального предел прочности при изгибе при определении продольно-крутильного изгиба. Причина этого фактора состоит в том, чтобы учесть неоднородные диаграммы моментов, когда концы сегмента балки скреплены. Консервативное значение для C_б может приниматься равным 1, независимо от конфигурации балки или нагрузки, но в некоторых случаях может быть чрезмерно консервативным. C_б всегда равно или больше 1, но не меньше. За консоли или выступы, свободный конец которых не закреплен, C_б равно 1. Таблицы значений C_б для просто поддерживаемых балок существуют.

Если подходящее значение C_б в таблицах не приводится, его можно получить по следующей формуле:

${\displaystyle C_{b}={\frac {12.5M_{\max }}{2.5M_{\max }+3M_{A}+4M_{B}+3M_{C}}}}$

куда

${\displaystyle M_{\max }}$, абсолютное значение максимального момента на свободном участке,

${\displaystyle M_{A}}$, абсолютное значение максимального момента в четверти свободного участка,

${\displaystyle M_{B}}$, абсолютное значение максимального момента на средней линии свободного сегмента,

${\displaystyle M_{C}}$, абсолютное значение максимального момента в трех четвертях свободного участка,

Результат одинаков для всех систем единиц.

Пластиковая коробочка

Прочность элемента на изгиб при изгибе меньше, чем прочность на изгиб при упругом изгибе конструкции, если материал элемента подвергается напряжению за пределами диапазона упругости материала и в диапазоне нелинейного (пластического) поведения материала. Когда сжимающая нагрузка близка к нагрузке продольного изгиба, конструкция будет значительно изгибаться, и материал колонны будет отклоняться от линейного поведения напряжения-деформации. Напряженно-деформированное поведение материалов не является строго линейным даже ниже предела текучести, следовательно, модуль упругости уменьшается по мере увеличения напряжения и значительно уменьшается по мере приближения напряжений к пределу текучести материала. Эта уменьшенная жесткость материала снижает сопротивление продольному изгибу конструкции и приводит к нагрузке при продольном изгибе, меньшей, чем прогнозируется в предположении линейного упругого поведения.

Более точное приближение нагрузки при продольном изгибе может быть получено с помощью тангенциального модуля упругости E_т, который меньше модуля упругости вместо модуля упругости. Касательная равна модулю упругости, а затем уменьшается сверх пропорционального предела. Касательный модуль - это линия, касательная к кривой напряжения-деформации при определенном значении деформации (в упругом участке кривой зависимости напряжения от деформации касательный модуль равен модулю упругости). Графики касательного модуля упругости для различных материалов доступны в стандартных справочных материалах.

Калечащий

Секции, состоящие из пластин с фланцами, например швеллер, могут по-прежнему нести нагрузку в углах после локального изгиба фланцев. Калечащий сбой - это сбой всего раздела.^[1]

Диагональное натяжение

Из-за тонкой обшивки, обычно используемой в аэрокосмической отрасли, обшивка может деформироваться при низких уровнях нагрузки. Однако, однажды изогнутые, вместо того, чтобы передавать поперечные силы, они все еще способны переносить нагрузку через диагональное напряжение (DT) напряжения в сети. Это приводит к нелинейному поведению несущей способности этих деталей. Отношение фактической нагрузки к нагрузке, при которой возникает коробление, известно как коэффициент продольного изгиба листа.^[1] Высокий коэффициент изгиба может привести к чрезмерному сморщиванию листов, которое затем может выйти из строя. уступающий от морщин. Хотя они могут коробиться, тонкие листы не деформируются постоянно и не возвращаются в расстегнутое состояние после снятия приложенной нагрузки. Повторяющееся коробление может привести к усталость неудачи.

Листы, находящиеся под диагональным растяжением, поддерживаются ребрами жесткости, которые в результате продольного изгиба несут распределенную нагрузку по всей своей длине, что, в свою очередь, может привести к разрушению этих конструктивных элементов при изгибе.

Более толстые пластины могут лишь частично образовывать диагональное поле растяжения и могут продолжать нести часть нагрузки за счет сдвига. Это известно как неполное диагональное натяжение (IDT). Это поведение было изучено Вагнером, и эти лучи иногда называют лучами Вагнера.^[1]

Диагональное натяжение также может привести к растягиванию любых крепежных деталей, таких как заклепки, которые используются для крепления полотна к опорным элементам. Крепежные детали и листы должны быть спроектированы так, чтобы их нельзя было сорвать с опор.

Динамическое изгибание

Если колонна нагружается внезапно, а затем нагрузка сбрасывается, колонна может выдержать гораздо более высокую нагрузку, чем ее статическая (медленно прикладываемая) нагрузка изгиба. Это может произойти в длинной колонне без опоры, используемой в качестве отбойного молотка. Продолжительность сжатия на ударном конце - это время, необходимое для того, чтобы волна напряжения прошла вдоль колонны до другого (свободного) конца и вернулась вниз в виде волны разгрузки. Максимальное продольное изгибание происходит около ударного конца при длине волны, намного меньшей, чем длина стержня, и при напряжении, во много раз превышающем напряжение продольного изгиба статически нагруженной колонны. Критическим условием для того, чтобы амплитуда продольного изгиба оставалась менее чем примерно в 25 раз превышающей эффективную прямолинейность стержня на длине волны изгиба, является

${\displaystyle \sigma L=\rho c^{2}h}$

куда ${\displaystyle \sigma }$ ударное напряжение, ${\displaystyle L}$ длина стержня, ${\displaystyle c}$ - скорость упругой волны, а ${\displaystyle h}$ - меньший поперечный размер прямоугольного стержня. Поскольку длина волны пряжки зависит только от ${\displaystyle \sigma }$ и ${\displaystyle h}$, эта же формула верна для тонких цилиндрических оболочек толщиной ${\displaystyle h}$.^[7]

Теория

Энергетический метод

Часто очень сложно определить точную нагрузку на продольный изгиб в сложных конструкциях с помощью формулы Эйлера из-за трудности определения постоянной K.Таким образом, максимальная нагрузка при продольном изгибе часто приближается с использованием энергосбережения и называется энергетическим методом в структурном анализе.

Первый шаг в этом методе - принять режим смещения и функцию, которая представляет это смещение. Эта функция должна удовлетворять наиболее важным граничным условиям, таким как смещение и вращение. Чем точнее функция смещения, тем точнее будет результат.

Метод предполагает, что система (колонна) является консервативной системой, в которой энергия не рассеивается в виде тепла, следовательно, энергия, добавленная к колонне за счет приложенных внешних сил, сохраняется в колонне в виде энергии деформации.

${\displaystyle U_{\text{applied}}=U_{\text{strain}}}$

В этом методе используются два уравнения (для малых деформаций) для аппроксимации энергии «деформации» (потенциальная энергия, запасенная в виде упругой деформации конструкции) и «приложенной» энергии (работа, совершаемая в системе внешними силами).

${\displaystyle {\begin{aligned}U_{\text{strain}}&={\frac {E}{2}}\int I(x)(w_{xx}(x))^{2}\,dx\\U_{\text{applied}}&={\frac {P_{\text{crit}}}{2}}\int (w_{x}(x))^{2}\,dx\end{aligned}}}$

куда ${\displaystyle w(x)}$ - функция смещения, а индексы ${\displaystyle x}$ и ${\displaystyle xx}$ относятся к первой и второй производным смещения.

Модели с одной степенью свободы

Используя концепцию полная потенциальная энергия, ${\displaystyle V}$, можно выделить четыре основные формы потери устойчивости, обнаруженные в моделях конструкций с одной степенью свободы. Начнем с выражения

${\displaystyle V=U-P\Delta }$

куда ${\displaystyle U}$ энергия деформации, запасенная в конструкции, ${\displaystyle P}$ применяется консервативный нагрузка и ${\displaystyle \Delta }$ расстояние, пройденное на ${\displaystyle P}$ в его направлении. Используя аксиомы теории упругой неустойчивости, а именно, что равновесие - это любая точка, в которой ${\displaystyle V}$ является стационарным относительно координаты, измеряющей степень (ы) свободы, и что эти точки устойчивы только в том случае, если ${\displaystyle V}$ является локальным минимумом и нестабильным в противном случае (например, максимум или точка перегиба).^[8]

Эти четыре формы упругого изгиба являются бифуркация седло-узел или же предельная точка; то сверхкритический или же стабильно-симметричный бифуркация; то субкритический или же неустойчиво-симметричный бифуркация; и транскритический или же асимметричный бифуркация. Все эти примеры, кроме первого, представляют собой форму вилы раздвоение. Простые модели для каждого из этих типов поведения потери устойчивости показаны на рисунках ниже вместе с соответствующими бифуркационными диаграммами.

Модели жестких звеньев с одной степенью свободы (SDoF), отображающие четыре различных типа явления потери устойчивости. Пружина в каждой модели не напряжена, когда ${\displaystyle q=0}$.

Предельная точка	Стабильно-симметричная бифуркация	Неустойчиво-симметричная бифуркация	Асимметричная бифуркация
Модель связанной фермы с наклонными звеньями и горизонтальной пружиной.	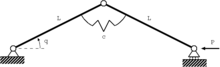Модель звена с вращающейся пружиной	Модель звена с поперечной пружиной	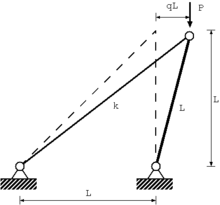Модель звена с наклонной пружиной

Бифуркационные диаграммы (синие) для вышеуказанных моделей с анимированной функцией энергии (красный) при различных значениях нагрузки, ${\displaystyle P}$ (чернить). Обратите внимание, нагрузка находится на вертикальной оси. Все графики представлены в безразмерном виде.

	${\displaystyle P^{C}=c/(2L)}$	${\displaystyle P^{C}=kL/2}$	${\displaystyle P^{C}=kL/2}$

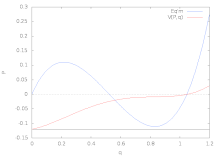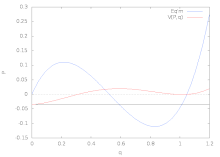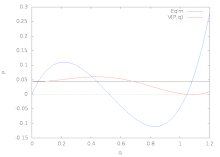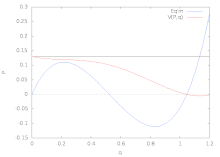Примеры инженерной мысли

Велосипедные колеса

Обычный велосипедное колесо состоит из тонкого обода, который выдерживает высокое сжимающее напряжение за счет (примерно нормального) тяги внутрь большого количества спиц. Его можно рассматривать как нагруженную колонну, согнутую по кругу. Если натяжение спиц превышает безопасный уровень или если часть обода подвергается определенной боковой силе, колесо самопроизвольно принимает характерную седловидную форму (иногда ее называют тако или тако).пронзить "), как трехмерная колонна Эйлера. Если это чисто упругая деформация, обод вернется в правильную плоскую форму, если будет уменьшено натяжение спиц или будет приложена поперечная сила с противоположного направления.

Дороги

Изгиб также является режимом отказа в тротуар материалы, в первую очередь бетон, так как асфальт более гибкий. Лучистое тепло от солнце впитывается в дорожное покрытие, вызывая расширять, заставляя соседние части прижиматься друг к другу. Если напряжение достаточно велико, тротуар может внезапно подняться и потрескаться. Переступать через секцию с пряжкой может быть очень неприятно. автомобиль драйверы, описанные как работающие над горка на скоростях шоссе.

Рельсовые пути

Железнодорожные пути в Нидерланды подвержены изгибу Солнца.

По аналогии, железнодорожные пути также расширяться при нагревании, и может выйти из строя из-за деформации, явление, называемое изгиб солнца. Рельсы чаще перемещаются в боковом направлении, часто натягивая нижележащие связи (спит) вместе.

Эти несчастные случаи были сочтены связанными с солнечным перегибом (дополнительная информация доступна на Список железнодорожных аварий (2000–2009 гг.) ):

• 18 апреля 2002 г. Amtrak Авто-поезд крушение, от CSX треки, рядом Кресент-Сити, Флорида.
• 29 июля 2002 г. Amtrak Capitol Limited крушение, от CSX треки, рядом Кенсингтон, Мэриленд.
• 8 июля 2010 г. Крушение поезда CSX в г. Уокшоу, Северная Каролина.
• 6 июля 2012 г. WMATA Metrorail крушение поезда рядом Станция West Hyattsville, Мэриленд.^[9]

Трубы и сосуды под давлением

Трубы и сосуды высокого давления подвергаются внешнему избыточному давлению, вызванному, например, охлаждением пара внутри трубы и конденсацией в воду с последующим значительным падением давления, риск потери устойчивости из-за сжатия кольцевые напряжения. Правила расчета необходимой толщины стенок или армирующих колец приведены в различных нормах для трубопроводов и сосудов высокого давления.

Смотрите также

• Критическая нагрузка Эйлера
• Формула Перри Робертсона
• Напряжение рельсов
• Придание жесткости
• Метод дерева
• Йошимура коробление

Рекомендации

1. Брун, Э. Ф. (1973). Анализ и проектирование конструкций летательных аппаратов. Индианаполис: Джейкобс.
2. Елисаков, И. Ли И-З. и Starnes, J.H. Мл., Неклассические задачи теории упругой устойчивости, Cambridge University Press, 2001, XVI + стр. 336; ISBN  0-521-78210-4
3. Като, К. (1915). "Математические исследования механических проблем линии передачи". Журнал Японского общества инженеров-механиков. 19: 41.
4. Ратцерсдорфер, Юлиус (1936). Die Knickfestigkeit von Stäben und Stabwerken [Сопротивление изгибу элементов и рам] (на немецком). Вайн, Австрия: J. Springer. С. 107–109. ISBN  978-3-662-24075-5.
5. Кокс, Стивен Дж .; К. Мейв Маккарти (1998). «Форма самой высокой колонны». Журнал СИАМ по математическому анализу. 29 (3): 547–554. Дои:10.1137 / s0036141097314537.
6. Булсон, П. С. (1970). Теория плоских пластин. Чатто и Виндус, Лондон.
7. Lindberg, H.E .; Флоренс, А. Л. (1987). Динамическое искривление пульса. Издательство Martinus Nijhoff. С. 11–56, 297–298.
8. Thompson, J.M.T .; Хант, Г. (1973). Общая теория упругой устойчивости. Лондон: Джон Вили. ISBN  9780471859918.
9. Лусеро, Кэт (07.07.2012). "Смещение пути из-за возможной причины перегрева в сходе с рельсов зеленой линии". DCist. Радио Американского университета. Архивировано из оригинал на 2018-02-04. Получено 2019-01-21.

дальнейшее чтение

• Тимошенко, С.; Гир, Дж. М. (1961). Теория упругой устойчивости. (2-е изд.). Макгроу-Хилл.
• Ненезич, М. (2004). «Механика термопластической сплошной среды». Журнал аэрокосмических структур. 4.
• Койтер, В. Т. (1945). Устойчивость упругого равновесия. (PDF) (Кандидатская диссертация).
• Раджеш, Дхакал; Маэкава, Коичи (2002). «Устойчивость арматуры и разрушение бетонного покрытия в железобетонных элементах». Журнал структурной инженерии. 128 (10): 1253–1262. Дои:10.1061 / (ASCE) 0733-9445 (2002) 128: 10 (1253). HDL:10092/4229.
• Сегуи, Виллиан Т. (2007). Стальной дизайн (Четвертое изд.). США: Томсон. ISBN  0-495-24471-6.
• Брун, Э. Ф. (1973). Анализ и проектирование конструкций летательных аппаратов. Индианаполис: Джейкобс.
• Елисаков, И. (2004). Разрешение загадки двадцатого века в области упругой устойчивости. Сингапур: World Scientific / Imperial College Press. ISBN  978-981-4583-53-4.

внешняя ссылка

• Полная теория и примеры экспериментальных результатов для длинных столбцов доступны в виде 39-страничного PDF-документа по адресу http://lindberglce.com/tech/buklbook.htm
• «Боковое продольное изгибание» (PDF). Архивировано из оригинал (PDF) 1 апреля 2010 г.`