Полиномиальная интерполяция - Polynomial interpolation

В числовой анализ, полиномиальная интерполяция это интерполяция данного набор данных посредством многочлен минимально возможной степени, которая проходит через точки набора данных.^[1]

Приложения

Полиномы можно использовать для аппроксимации сложных кривых, например формы букв в типография,^{[нужна цитата ]} дали несколько баллов. Соответствующее приложение - это оценка натуральный логарифм и тригонометрические функции: выберите несколько известных точек данных, создайте Справочная таблица, и интерполировать между этими точками данных. Это приводит к значительно более быстрым вычислениям.^{[уточнить ]} Полиномиальная интерполяция также составляет основу алгоритмов в числовая квадратура и числовые обыкновенные дифференциальные уравнения и Безопасные многосторонние вычисления, Обмен секретами схемы.

Полиномиальная интерполяция также необходима для выполнения субквадратичного умножения и возведения в квадрат, например Умножение Карацубы и Умножение Тоома – Кука, где интерполяция по точкам многочлена, определяющего продукт, дает само произведение. Например, учитывая а = ж(Икс) = а₀Икс⁰ + а₁Икс¹ + ... и б = грамм(Икс) = б₀Икс⁰ + б₁Икс¹ + ..., товар ab эквивалентно W(Икс) = ж(Икс)грамм(Икс). Поиск точек вдоль W(Икс) путем замены Икс для малых значений в ж(Икс) и грамм(Икс) дает точки на кривой. Интерполяция, основанная на этих точках, даст условия W(Икс) и впоследствии продукт ab. В случае умножения Карацубы этот метод значительно быстрее, чем квадратное умножение, даже для входов небольшого размера. Это особенно актуально при использовании параллельного оборудования.

Определение

Учитывая набор п + 1 точки данных (Икс_я, у_я) где нет двух Икс_я одинаковы, многочлен ${\displaystyle p:\mathbb {R} \rightarrow \mathbb {R} }$ говорят интерполировать данные, если ${\displaystyle p(x_{j})=y_{j}}$ для каждого ${\displaystyle j\in \{0,1,\dotsc ,n\}}$.

Теорема интерполяции

Данный ${\displaystyle n+1}$ отдельные точки ${\displaystyle x_{0},x_{1},\dotsc ,x_{n}}$ и соответствующие значения ${\displaystyle y_{0},y_{1},\dotsc ,y_{n}}$, существует единственный полином степени не выше ${\displaystyle n}$ который интерполирует данные ${\displaystyle \{(x_{0},y_{0}),\dotsc ,(x_{n},y_{n})\}}$.^[2]

Доказательство

Рассмотрим базисные функции Лагранжа:

${\displaystyle L_{n,j}(x)=\prod _{k\neq j}{\frac {x-x_{k}}{x_{j}-x_{k}}}}$.

Заметь ${\displaystyle L_{n,j}}$ является многочленом степени ${\displaystyle n}$. Кроме того, для каждого ${\displaystyle x_{k}}$ у нас есть ${\displaystyle L_{n,j}(x_{k})=\delta _{jk}}$, куда ${\displaystyle \delta _{jk}}$ это Дельта Кронекера. Отсюда следует, что линейная комбинация

${\displaystyle p(x)=\sum _{j=0}^{n}y_{j}L_{n,j}(x)}$

- интерполирующий полином степени ${\displaystyle n}$.

Чтобы доказать единственность, предположим, что существует другой интерполирующий многочлен ${\displaystyle q}$ степени не более ${\displaystyle n}$. С ${\displaystyle p(x_{k})=q(x_{k})}$ для всех ${\displaystyle k=0,\dotsc ,n}$, следует, что многочлен ${\displaystyle p-q}$ имеет ${\displaystyle n+1}$ отличные нули. Однако, ${\displaystyle p-q}$ имеет степень не выше ${\displaystyle n}$ и, по основная теорема алгебры^[3], может иметь самое большее ${\displaystyle n}$ нули; следовательно, ${\displaystyle p=q}$.

Следствие

Интересным следствием интерполяционной теоремы является то, что если ${\displaystyle f}$ является многочленом степени не выше ${\displaystyle n}$, то интерполяционный многочлен от ${\displaystyle f}$ в ${\displaystyle n+1}$ отдельные точки ${\displaystyle f}$ сам.

Теорема единственности

Учитывая набор п + 1 точки данных (Икс_я, у_я) где нет двух Икс_я одинаковы, ищется многочлен п степени не более п с собственностью

${\displaystyle p(x_{i})=y_{i},\qquad i=0,\ldots ,n.}$

В неразрывность Теорема утверждает, что такой многочлен п существует и единственна и может быть доказана Матрица Вандермонда, как описано ниже.

Теорема утверждает, что для п + 1 узлы интерполяции (Икс_я), полиномиальная интерполяция определяет линейную биекция

${\displaystyle L_{n}:\mathbb {K} ^{n+1}\to \Pi _{n}}$

где Π_п это векторное пространство многочленов (определенных на любом интервале, содержащем узлы) степени не выше п.

Построение интерполяционного полинома

Основная статья: Полином Лагранжа

Красные точки обозначают точки данных (Икс_k, у_k), а синяя кривая показывает полином интерполяции.

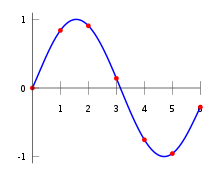
Предположим, что интерполяционный полином имеет вид

${\displaystyle p(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_{2}x^{2}+a_{1}x+a_{0}.\qquad (1)}$

Заявление о том, что п интерполирует точки данных означает, что

${\displaystyle p(x_{i})=y_{i}\qquad {\mbox{for all }}i\in \left\{0,1,\dots ,n\right\}.}$

Если мы подставим сюда уравнение (1), мы получим система линейных уравнений в коэффициентах а_k. Система в матрично-векторной форме читает следующее умножение:

${\displaystyle {\begin{bmatrix}x_{0}^{n}&x_{0}^{n-1}&x_{0}^{n-2}&\ldots &x_{0}&1\\x_{1}^{n}&x_{1}^{n-1}&x_{1}^{n-2}&\ldots &x_{1}&1\\\vdots &\vdots &\vdots &&\vdots &\vdots \\x_{n}^{n}&x_{n}^{n-1}&x_{n}^{n-2}&\ldots &x_{n}&1\end{bmatrix}}{\begin{bmatrix}a_{n}\\a_{n-1}\\\vdots \\a_{0}\end{bmatrix}}={\begin{bmatrix}y_{0}\\y_{1}\\\vdots \\y_{n}\end{bmatrix}}.}$

Мы должны решить эту систему за а_k построить интерполянт п(Икс). Матрица слева обычно называется Матрица Вандермонда.

В номер условия матрицы Вандермонда может быть большой,^[4] вызывая большие ошибки при вычислении коэффициентов а_я если система уравнений решается с использованием Гауссово исключение.

Поэтому несколько авторов предложили алгоритмы, которые используют структуру матрицы Вандермонда для вычисления численно устойчивых решений в O (п²) вместо операций O (п³), требуемого методом исключения Гаусса.^[5][6][7] Эти методы основаны на построении сначала Интерполяция Ньютона полинома, а затем преобразовав его в мономиальная форма над.

В качестве альтернативы мы можем записать многочлен сразу через Полиномы Лагранжа:

${\displaystyle {\begin{aligned}p(x)&={\frac {(x-x_{1})(x-x_{2})\cdots (x-x_{n})}{(x_{0}-x_{1})(x_{0}-x_{2})\cdots (x_{0}-x_{n})}}y_{0}+{\frac {(x-x_{0})(x-x_{2})\cdots (x-x_{n})}{(x_{1}-x_{0})(x_{1}-x_{2})\cdots (x_{1}-x_{n})}}y_{1}+\ldots +{\frac {(x-x_{0})(x-x_{1})\cdots (x-x_{n-1})}{(x_{n}-x_{0})(x_{n}-x_{1})\cdots (x_{n}-x_{n-1})}}y_{n}\\&=\sum _{i=0}^{n}\left(\prod _{\stackrel {\!0\leq j\leq n}{j\neq i}}{\frac {x-x_{j}}{x_{i}-x_{j}}}\right)y_{i}\end{aligned}}}$

Для матричных аргументов эта формула называется Формула Сильвестра а матричнозначные полиномы Лагранжа - Коварианты Фробениуса.

Единственность интерполирующего полинома

Доказательство 1

Предположим, мы интерполируем через п + 1 точки данных с не более чем п многочлен степени п(Икс) (нам нужно как минимум п + 1 точки данных, иначе полином не может быть полностью решен). Предположим также, что существует еще один многочлен также степени не выше п который также интерполирует п + 1 точки; назови это q(Икс).

Учитывать ${\displaystyle r(x)=p(x)-q(x)}$. Мы знаем,

1. р(Икс) - многочлен
2. р(Икс) имеет степень не выше п, поскольку п(Икс) и q(Икс) не выше этого значения, и мы их просто вычитаем.
3. На п + 1 точки данных, ${\displaystyle r(x_{i})=p(x_{i})-q(x_{i})=y_{i}-y_{i}=0}$. Следовательно, р(Икс) имеет п + 1 корни.

Но р(Икс) - многочлен степени ≤ п. У него один корень слишком много. Формально, если р(Икс) - любой ненулевой многочлен, он должен быть записан как ${\displaystyle r(x)=A(x-x_{0})(x-x_{1})\cdots (x-x_{n})}$, для некоторой постоянной А. По распределительности п + 1 Икс's умножить вместе, чтобы получить главный член ${\displaystyle Ax^{n+1}}$, т.е. на один градус выше установленного нами максимума. Так что единственный способ р(Икс) может существовать, если А = 0, или эквивалентно, р(Икс) = 0.

${\displaystyle r(x)=0=p(x)-q(x)\implies p(x)=q(x)}$

Так q(Икс) (который может быть любым полиномом, если он интерполирует точки) идентичен п(Икс), и q(Икс) уникален.

Доказательство 2

Учитывая матрицу Вандермонда, использованную выше для построения интерполянта, мы можем настроить систему

${\displaystyle Va=y}$

Чтобы доказать, что V является неособый используем формулу определителя Вандермонда:

${\displaystyle \det(V)=\prod _{i,j=0,i<j}^{n}(x_{i}-x_{j})}$

так как п + 1 точки различны, детерминант не может быть нулем как ${\displaystyle x_{i}-x_{j}}$ никогда не равно нулю, поэтому V неособа и система имеет единственное решение.

В любом случае это означает, что независимо от того, какой метод мы используем для интерполяции: прямой, Лагранж и т. д. (при условии, что мы можем делать все наши вычисления идеально), мы всегда будем получать один и тот же полином.

Решения, не связанные с Vandermonde

Мы пытаемся построить наш уникальный интерполяционный полином в векторном пространстве Π_п многочленов степени п. При использовании мономиальный базис для Π_п мы должны решить матрицу Вандермонда, чтобы построить коэффициенты а_k для интерполяционного полинома. Это может быть очень дорогостоящей операцией (если считать в тактовых циклах компьютера, пытающегося выполнить эту работу). Выбирая другую основу для Π_п мы можем упростить вычисление коэффициентов, но тогда нам придется провести дополнительные вычисления, когда мы хотим выразить интерполяционный полином через мономиальный базис.

Один из способов - записать полином интерполяции в Форма Ньютона и использовать метод разделенные различия для построения коэффициентов, например Алгоритм Невилла. Стоимость составляет O (п²) операций, а исключение Гаусса стоит O (п³) операции. Кроме того, вам нужно всего лишь O (п) дополнительная работа, если к набору данных добавлена ​​дополнительная точка, тогда как для других методов вам придется повторить все вычисления.

Другой метод - использовать Форма Лагранжа интерполяционного полинома. Полученная формула сразу показывает, что интерполяционный полином существует при условиях, сформулированных в приведенной выше теореме. Формула Лагранжа предпочтительнее формулы Вандермонда, когда нас интересует не вычисление коэффициентов многочлена, а вычисление значения п(Икс) в данном Икс нет в исходном наборе данных. В этом случае мы можем снизить сложность до O (п²).^[8]

В Форма Бернштейна был использован в конструктивном доказательстве Аппроксимационная теорема Вейерштрасса к Бернштейн и приобрел большое значение в компьютерной графике в виде Кривые Безье.

Линейное сочетание заданных значений

В Форма Лагранжа интерполирующего полинома представляет собой линейную комбинацию заданных значений. Во многих сценариях эффективная и удобная полиномиальная интерполяция линейная комбинация заданных значений, используя ранее известные коэффициенты. Учитывая набор ${\displaystyle k+1}$ точки данных ${\displaystyle (x_{0},y_{0}),\ldots ,(x_{j},y_{j}),\ldots ,(x_{k},y_{k})}$ где каждая точка данных представляет собой пару (положение, значение) и где нет двух позиций ${\displaystyle x_{j}}$ одинаковы, интерполяционный многочлен в форме Лагранжа является линейная комбинация

${\displaystyle y(x):=\sum _{j=0}^{k}y_{j}c_{j}(x)}$

данных значений ${\displaystyle y_{j}}$ с каждым коэффициентом ${\displaystyle c_{j}(x)}$ дается вычислением соответствующего базисного полинома Лагранжа с использованием данного ${\displaystyle k+1}$ позиции ${\displaystyle x_{j}}$.

${\displaystyle c_{j}(x)=\ell _{j}(x,x_{0},x_{1},\ldots ,x_{k}):=\prod _{\begin{smallmatrix}0\leq m\leq k\\m\neq j\end{smallmatrix}}{\frac {x-x_{m}}{x_{j}-x_{m}}}={\frac {(x-x_{0})}{(x_{j}-x_{0})}}\cdots {\frac {(x-x_{j-1})}{(x_{j}-x_{j-1})}}{\frac {(x-x_{j+1})}{(x_{j}-x_{j+1})}}\cdots {\frac {(x-x_{k})}{(x_{j}-x_{k})}}.}$

Геометрическая интерпретация кубической интерполяции черной точки с равномерно расположенными абсциссами.^[9]

Каждый коэффициент ${\displaystyle c_{j}(x)}$ в линейной комбинации зависит от заданных позиций ${\displaystyle x_{j}}$ и желаемое положение ${\displaystyle x}$, но не на заданных значениях ${\displaystyle y_{j}}$. Для каждого коэффициента, вставляя значения заданных позиций ${\displaystyle x_{j}}$ и упрощение дает выражение ${\displaystyle c_{j}(x)}$, который зависит только от ${\displaystyle x}$. Таким образом, те же выражения коэффициентов ${\displaystyle c_{j}(x)}$ может использоваться в полиномиальной интерполяции данного второго набора ${\displaystyle k+1}$ точки данных ${\displaystyle (x_{0},v_{0}),\ldots ,(x_{j},v_{j}),\ldots ,(x_{k},v_{k})}$ на тех же должностях ${\displaystyle x_{j}}$, где вторые заданные значения ${\displaystyle v_{j}}$ отличаются от первых заданных значений ${\displaystyle y_{j}}$. Используя те же выражения коэффициентов ${\displaystyle c_{j}(x)}$ что касается первого набора точек данных, полином интерполяции второго набора точек данных представляет собой линейную комбинацию

${\displaystyle v(x):=\sum _{j=0}^{k}v_{j}c_{j}(x).}$

Для каждого коэффициента ${\displaystyle c_{j}(x)}$ в линейной комбинации выражение, полученное из базисного полинома Лагранжа ${\displaystyle \ell _{j}(x,x_{0},x_{1},\ldots ,x_{k})}$ зависит только от относительных пробелов между данными позициями, а не от индивидуального значения какой-либо позиции. Таким образом, те же выражения коэффициентов ${\displaystyle c_{j}(x)}$ может использоваться в полиномиальной интерполяции данного третьего набора ${\displaystyle k+1}$ точки данных

${\displaystyle (t_{0},w_{0}),\ldots ,(t_{j},w_{j}),\ldots ,(t_{k},w_{k})}$

где каждая позиция ${\displaystyle t_{j}}$ относится к соответствующей позиции ${\displaystyle x_{j}}$ в первом наборе ${\displaystyle t_{i}=a*x_{i}+b}$ и желаемые позиции связаны соотношением ${\displaystyle t=a*x+b}$, для постоянного масштабного коэффициента а и постоянный сдвиг б для всех позиций. Используя те же выражения коэффициентов ${\displaystyle c_{j}(t)}$ что касается первого набора точек данных, полином интерполяции третьего набора точек данных представляет собой линейную комбинацию

${\displaystyle w(t):=\sum _{j=0}^{k}w_{j}c_{j}(t).}$

Во многих приложениях полиномиальной интерполяции заданный набор ${\displaystyle k+1}$ точки данных находятся на одинаковом расстоянии друг от друга. В этом случае может быть удобно определить Икс-оси позиций такие, что ${\displaystyle x_{i}=i}$. Например, заданный набор из 3 равноотстоящих точек данных ${\displaystyle (x_{0},y_{0}),(x_{1},y_{1}),(x_{2},y_{2})}$ затем ${\displaystyle (0,y_{0}),(1,y_{1}),(2,y_{2})}$.

Интерполяционный полином в форме Лагранжа - это линейная комбинация

${\displaystyle {\begin{aligned}y(x):=\sum _{j=0}^{2}y_{j}c_{j}(x)=y_{0}{\frac {(x-1)(x-2)}{(0-1)(0-2)}}+y_{1}{\frac {(x-0)(x-2)}{(1-0)(1-2)}}+y_{2}{\frac {(x-0)(x-1)}{(2-0)(2-1)}}\\=y_{0}{\frac {(x-1)(x-2)}{2}}+y_{1}{\frac {(x-0)(x-2)}{-1}}+y_{2}{\frac {(x-0)(x-1)}{2}}.\end{aligned}}}$

Эта квадратичная интерполяция действительна для любой позиции. Икс, рядом или далеко от заданных позиций. Итак, учитывая 3 равноотстоящих точки данных в ${\displaystyle x=0,1,2}$ определение квадратичного полинома в желаемой позиции примера ${\displaystyle x=1.5}$, интерполированное значение после упрощения имеет вид ${\displaystyle y(1.5)=y_{1.5}=(-y_{0}+6y_{1}+3y_{2})/8}$

Это квадратичная интерполяция, обычно используемая в многосеточном методе. Снова даны 3 равноотстоящие точки данных на ${\displaystyle x=0,1,2}$ определяющий квадратичный многочлен в следующей равноотстоящей позиции ${\displaystyle x=3}$, интерполированное значение после упрощения имеет вид

${\displaystyle y(3)=y_{3}=y_{0}-3y_{1}+3y_{2}}$

В приведенных выше полиномиальных интерполяциях с использованием линейной комбинации заданных значений коэффициенты определялись с использованием метода Лагранжа. В некоторых сценариях коэффициенты легче определить с помощью других методов. Примеры приведены ниже.

Согласно метод конечных разностей, для любого полинома степени d или меньше, любая последовательность ${\displaystyle d+2}$ значения в равноотстоящих позициях имеет ${\displaystyle (d+1)}$-я разность точно равна 0. Элемент s_{d + 1} из Биномиальное преобразование такой ${\displaystyle (d+1)}$-я разница. Здесь исследуется эта территория.^[10] В биномиальное преобразование, Т, последовательности значений {v_п}, это последовательность {s_п} определяется

${\displaystyle s_{n}=\sum _{k=0}^{n}(-1)^{k}{n \choose k}v_{k}.}$

Игнорирование знакового термина ${\displaystyle (-1)^{k}}$, то ${\displaystyle n+1}$ коэффициенты элемента s_п соответствующие ${\displaystyle n+1}$ элементы ряда п треугольника Паскаля. В треугольник коэффициентов биномиального преобразования похож на треугольник Паскаля. Запись в пй ряд и kстолбец треугольника BTC ${\displaystyle (-1)^{k}{\tbinom {n}{k}}}$ для любого неотрицательного целого числа п и любое целое число k от 0 до п. Это приводит к следующим примерам строк п = 0 через п = 7, сверху вниз, для треугольника BTC:

								1									Ряд n = 0
							1		−1								Строка n = 1 или d = 0
						1		−2		1							Ряд n = 2 или d = 1
					1		−3		3		−1						Ряд n = 3 или d = 2
				1		−4		6		−4		1					Ряд n = 4 или d = 3
			1		−5		10		−10		5		−1				Ряд n = 5 или d = 4
		1		−6		15		−20		15		−6		1			Ряд n = 6 или d = 5
	1		−7		21		−35		35		−21		7		−1		Ряд n = 7 или d = 6

Для удобства каждый ряд п в приведенном выше примере треугольник BTC также имеет метку ${\displaystyle d=n-1}$. Таким образом, для любого полинома степени d или меньше, любая последовательность ${\displaystyle d+2}$ значения в равноотстоящих позициях имеет линейная комбинация результат 0, при использовании ${\displaystyle d+2}$ элементы ряда d как соответствующие линейные коэффициенты.

Например, 4 равноотстоящих точки данных квадратичного многочлена подчиняются линейное уравнение задано строкой ${\displaystyle d=2}$ треугольника BTC. ${\displaystyle 0=y_{0}-3y_{1}+3y_{2}-y_{3}}$ Это то же линейное уравнение, которое получено выше с использованием метода Лагранжа.

Треугольник BTC также можно использовать для получения других полиномиальных интерполяций. Например, приведенная выше квадратичная интерполяция

${\displaystyle y(1.5)=y_{1.5}=(-y_{0}+6y_{1}+3y_{2})/8}$

может быть получено за 3 простых шага следующим образом. Равноотстоящие точки квадратичного многочлена подчиняются строкам треугольника BTC с ${\displaystyle d=2}$ или выше. Во-первых, ряд ${\displaystyle d=3}$ охватывает заданные и желаемые точки данных ${\displaystyle y_{0},y_{1},y_{1.5},y_{2}}$ с линейным уравнением

${\displaystyle 0=1y_{0}-4y_{0.5}+6y_{1}-4y_{1.5}+1y_{2}}$

Во-вторых, нежелательная точка данных ${\displaystyle y_{0.5}}$ заменяется выражением с точки зрения требуемых точек данных. Ряд ${\displaystyle d=2}$ дает линейное уравнение с членом ${\displaystyle 1y_{0.5}}$, что приводит к термину ${\displaystyle 4y_{0.5}}$ умножив линейное уравнение на 4. ${\displaystyle 0=1y_{0.5}-3y_{1}+3y_{1.5}-1y_{2}=4y_{0.5}-12y_{1}+12y_{1.5}-4y_{2}}$ В-третьих, два вышеуказанных линейных уравнения добавляются, чтобы получить линейное уравнение, эквивалентное приведенной выше квадратичной интерполяции для ${\displaystyle y_{1.5}}$. ${\displaystyle 0=(1+0)y_{0}+(-4+4)y_{0.5}+(6-12)y_{1}+(-4+12)y_{1.5}+(1-4)y_{2}=y_{0}-6y_{1}+8y_{1.5}-3y_{2}}$

Как и в других случаях использования линейных уравнений, приведенный выше вывод масштабирует и добавляет векторы коэффициентов. При полиномиальной интерполяции как линейной комбинации значений элементы вектора соответствуют непрерывной последовательности регулярно расположенных позиций. В п ненулевые элементы вектора - это п коэффициентов в линейном уравнении, которому подчиняется любая последовательность п точки данных с любой степенью d полином на любой регулярной сетке, где d отмечается индексом вектора. Для любого вектора коэффициентов индекс подчиняется ${\displaystyle d\leq p-2}$. При добавлении векторов с различными значениями нижнего индекса для результирующего вектора применяется самый нижний индекс. Итак, начиная с вектора строки ${\displaystyle d=3}$ и вектор строки ${\displaystyle d=2}$ треугольника BTC, приведенная выше квадратичная интерполяция для ${\displaystyle y_{1.5}}$ выводится вычислением вектора

${\displaystyle (1,-4,6,-4,1)_{3}+4*(0,1,-3,3,-1)_{2}=(1,0,-6,+8,-3)_{2}}$

Аналогичным образом, кубическая интерполяция, типичная для Многосеточный метод,

${\displaystyle y_{1.5}=(-y_{0}+9y_{1}+9y_{2}-y_{3})/16,}$

может быть получено вычислением вектора, начиная с вектора строки ${\displaystyle d=5}$ и вектор строки ${\displaystyle d=3}$ треугольника BTC.

${\displaystyle (1,-6,15,-20,15,-6,1)_{5}+6*(0,1,-4,6,-4,1,0)_{3}=(1,0,-9,16,-9,0,1)_{3}}$

Ошибка интерполяции

При интерполяции заданной функции ж полиномом степени п в узлах Икс₀,...,Икс_п мы получаем ошибку

${\displaystyle f(x)-p_{n}(x)=f[x_{0},\ldots ,x_{n},x]\prod _{i=0}^{n}(x-x_{i})}$

куда

${\displaystyle f[x_{0},\ldots ,x_{n},x]}$

это обозначение для разделенные различия.

Если ж является п + 1 раз, непрерывно дифференцируемые на отрезке я и ${\displaystyle p_{n}(x)}$ является многочленом степени не выше п что интерполирует ж в п + 1 отдельные точки {Икс_я} (я= 0,1, ..., n) в этом интервале, то для каждого x в интервале существует ξ в том интервале, что

${\displaystyle f(x)-p_{n}(x)={\frac {f^{(n+1)}(\xi )}{(n+1)!}}\prod _{i=0}^{n}(x-x_{i}).}$

Приведенная выше граница ошибки предлагает выбрать точки интерполяции Икс_я так что продукт ${\displaystyle \left|\prod (x-x_{i})\right|,}$ как можно меньше. В Чебышевские узлы добиться этого.

Доказательство

Задайте срок ошибки как

${\displaystyle R_{n}(x)=f(x)-p_{n}(x)}$

и настроить вспомогательную функцию:

${\displaystyle Y(t)=R_{n}(t)-{\frac {R_{n}(x)}{W(x)}}W(t)}$

куда

${\displaystyle W(t)=\prod _{i=0}^{n}(t-x_{i})}$

С Икс_я корни ${\displaystyle R_{n}(t)}$ и ${\displaystyle W(t)}$, у нас есть Y(Икс) = Y(Икс_я) = 0, что значит Y имеет по крайней мере п + 2 корни. Из Теорема Ролля, ${\displaystyle Y^{\prime }(t)}$ имеет по крайней мере п + 1 корни, тогда ${\displaystyle Y^{(n+1)}(t)}$ имеет хотя бы один корень ξ, куда ξ находится в интервале я.

Итак, мы можем получить

${\displaystyle Y^{(n+1)}(t)=R_{n}^{(n+1)}(t)-{\frac {R_{n}(x)}{W(x)}}\ (n+1)!}$

С ${\displaystyle p_{n}(x)}$ является многочленом степени не выше п, тогда

${\displaystyle R_{n}^{(n+1)}(t)=f^{(n+1)}(t)}$

Таким образом

${\displaystyle Y^{(n+1)}(t)=f^{(n+1)}(t)-{\frac {R_{n}(x)}{W(x)}}\ (n+1)!}$

С ξ это корень ${\displaystyle Y^{(n+1)}(t)}$, так

${\displaystyle Y^{(n+1)}(\xi )=f^{(n+1)}(\xi )-{\frac {R_{n}(x)}{W(x)}}\ (n+1)!=0}$

Следовательно,

${\displaystyle R_{n}(x)=f(x)-p_{n}(x)={\frac {f^{(n+1)}(\xi )}{(n+1)!}}\prod _{i=0}^{n}(x-x_{i})}$.

Таким образом, остаточный член в форме Лагранжа Теорема Тейлора является частным случаем ошибки интерполяции, когда все узлы интерполяции Икс_я идентичны.^[11] Обратите внимание, что ошибка будет равна нулю, когда ${\displaystyle x=x_{i}}$ для любого я. Таким образом, максимальная ошибка произойдет в некоторый момент в интервале между двумя последовательными узлами.

Для равномерных интервалов

В случае равноотстоящих узлов интерполяции, когда ${\displaystyle x_{i}=a+ih}$, за ${\displaystyle i=0,1,\ldots ,n,}$ и где ${\displaystyle h=(b-a)/n,}$ член продукта в формуле ошибки интерполяции может быть ограничен как^[12]

${\displaystyle \left|\prod _{i=0}^{n}(x-x_{i})\right|=\prod _{i=0}^{n}\left|x-x_{i}\right|\leq {\frac {n!}{4}}h^{n+1}}$.

Таким образом, граница ошибки может быть задана как

${\displaystyle \left|R_{n}(x)\right|\leq {\frac {h^{n+1}}{4(n+1)}}\max _{\xi \in [a,b]}\left|f^{(n+1)}(\xi )\right|}$

Однако это предполагает, что ${\displaystyle f^{(n+1)}(\xi )}$ преобладают ${\displaystyle h^{n+1}}$, т.е. ${\displaystyle f^{(n+1)}(\xi )h^{n+1}\ll 1}$. В некоторых случаях это неверно, и ошибка фактически увеличивается по мере того, как п → ∞ (видеть Феномен Рунге ). Этот вопрос рассматривается в раздел Свойства сходимости.

Константы Лебега

Смотрите основную статью: Постоянная Лебега.

Закрепляем узлы интерполяции Икс₀, ..., Икс_п и интервал [а, б], содержащий все узлы интерполяции. Процесс интерполяции отображает функцию ж к многочлену п. Это определяет отображение Икс из космоса C([а, б]) всех непрерывных функций на [а, б] себе. Карта Икс линейна, и это проекция на подпространстве Π_п многочленов степени п или менее.

Постоянная Лебега L определяется как норма оператора из Икс. Один имеет (частный случай Лемма Лебега ):

${\displaystyle \|f-X(f)\|\leq (L+1)\|f-p^{*}\|.}$

Другими словами, интерполяционный полином не более чем множитель (L +1) хуже наилучшего возможного приближения. Это говорит о том, что мы ищем набор узлов интерполяции, который делает L маленький. В частности, для Чебышевские узлы:

${\displaystyle L\leq {\frac {2}{\pi }}\log(n+1)+1.}$

Мы снова заключаем, что узлы Чебышева - очень хороший выбор для полиномиальной интерполяции, так как рост п экспоненциально для равноудаленных узлов. Однако эти узлы не оптимальны.

Свойства сходимости

Естественно спросить, для каких классов функций и для каких узлов интерполяции последовательность интерполирующих полиномов сходится к интерполированной функции как п → ∞? Конвергенцию можно понимать по-разному, например: поточечно, равномерно или в некоторой интегральной норме.

Ситуация довольно плохая для равноудаленных узлов, поскольку равномерная сходимость не гарантируется даже для бесконечно дифференцируемых функций. Один классический пример, из-за Карла Рунге, - функция ж(Икс) = 1 / (1 + Икс²) на интервале [−5, 5]. Ошибка интерполяции || ж − п_п||_∞ растет без ограничений, как п → ∞. Другой пример - функция ж(Икс) = |Икс| на интервале [−1, 1], для которых интерполирующие полиномы даже не сходятся поточечно, кроме трех точек Икс = ±1, 0.^[13]

Можно подумать, что лучшие свойства сходимости можно получить, выбирая разные узлы интерполяции. Следующий результат, кажется, дает довольно обнадеживающий ответ:

Теорема. Для любой функции ж(Икс) непрерывна на отрезке [а,б] существует таблица узлов, для которых последовательность интерполирующих многочленов ${\displaystyle p_{n}(x)}$ сходится к ж(Икс) равномерно на [а,б].

Доказательство. Понятно, что последовательность полиномов наилучшего приближения ${\displaystyle p_{n}^{*}(x)}$ сходится к ж(Икс) равномерно (за счет Аппроксимационная теорема Вейерштрасса ). Осталось только показать, что каждый ${\displaystyle p_{n}^{*}(x)}$ может быть получен путем интерполяции на определенных узлах. Но это верно из-за особого свойства многочленов наилучшего приближения, известного из теорема о равных колебаниях. В частности, мы знаем, что такие многочлены должны пересекаться ж(Икс) по меньшей мере п + 1 раз. Выбирая точки пересечения в качестве узлов интерполяции, мы получаем интерполирующий полином, совпадающий с полиномом наилучшего приближения.

Однако недостатком этого метода является то, что узлы интерполяции должны вычисляться заново для каждой новой функции. ж(Икс), но алгоритм сложно реализовать численно. Существует ли единая таблица узлов, для которой последовательность интерполирующих полиномов сходится к любой непрерывной функции ж(Икс)? К сожалению, ответ отрицательный:

Теорема. Для любой таблицы узлов существует непрерывная функция ж(Икс) на интервале [а, б], для которого последовательность интерполяционных многочленов расходится на [а,б].^[14]

Доказательство существенно использует оценку снизу константы Лебега, которую мы определили выше как операторную норму Икс_п (куда Икс_п - оператор проектирования на Π_п). Теперь ищем таблицу узлов, для которых

${\displaystyle \lim _{n\to \infty }X_{n}f=f,{\text{ for every }}f\in C([a,b]).}$

Из-за Теорема Банаха – Штейнгауза, это возможно только при соблюдении норм Икс_п равномерно ограничены, что не может быть истинным, поскольку мы знаем, что

${\displaystyle \|X_{n}\|\geq {\tfrac {2}{\pi }}\log(n+1)+C.}$

Например, если в качестве узлов интерполяции выбраны эквидистантные точки, функция из Феномен Рунге демонстрирует расхождение такой интерполяции. Заметим, что эта функция не только непрерывна, но даже бесконечно дифференцируема на [−1, 1]. К лучшему Чебышевские узлы Однако найти такой пример гораздо сложнее из-за следующего результата:

Теорема. Для каждого абсолютно непрерывный функционировать на [−1, 1] последовательность интерполяционных многочленов, построенная на чебышевских узлах, сходится кж(Икс) равномерно.^[15]

Связанные понятия

Феномен Рунге показывает, что для высоких значений п, полином интерполяции может сильно колебаться между точками данных. Эта проблема обычно решается с помощью сплайн-интерполяция. Здесь интерполянт не полином, а сплайн: цепочка из нескольких полиномов более низкой степени.

Интерполяция периодические функции к гармонический функции выполняются преобразование Фурье. Это можно рассматривать как форму полиномиальной интерполяции с гармоническими базовыми функциями, см. тригонометрическая интерполяция и тригонометрический полином.

Эрмита интерполяция проблемы - это те, где не только значения многочлена п в узлах даны, а также все производные до заданного порядка. Это оказывается эквивалентным системе одновременных полиномиальных сравнений и может быть решено с помощью Китайская теорема об остатках для полиномов. Интерполяция Биркгофа является дальнейшим обобщением, в котором предписаны только производные некоторых порядков, а не обязательно всех порядков от 0 до k.

Методы коллокации для решения дифференциальных и интегральных уравнений основаны на полиномиальной интерполяции.

Техника моделирование рациональных функций является обобщением, которое рассматривает отношения полиномиальных функций.

Наконец, многомерная интерполяция для более высоких измерений.

Смотрите также

• Серия Ньютон
• Полиномиальная регрессия

Примечания

1. Тиман, Джером Дж. (Май – июнь 1981 г.). «Полиномиальная интерполяция». Новости ввода / вывода. 1 (5): 16. ISSN  0274-9998. Получено 3 ноября 2017.
2. Хамферис, Джеффри; Джарвис, Тайлер Дж. (2020). «9.2 - Интерполяция». Основы прикладной математики Том 2: алгоритмы, аппроксимация, оптимизация. Общество промышленной и прикладной математики. п. 418. ISBN  978-1-611976-05-2.
3. Хамферис, Джеффри; Джарвис, Тайлер Дж .; Эванс, Эмили Дж. (2017). «15.3: Основная теорема арифметики». Основы прикладной математики Том 1: Математический анализ. Общество промышленной и прикладной математики. п. 591. ISBN  978-1-611974-89-8.
4. Гаучи, Уолтер (1975). "Оценки норм для инверсий матриц Вандермонда". Numerische Mathematik. 23 (4): 337–347. Дои:10.1007 / BF01438260.
5. Хайэм, Н. Дж. (1988). «Быстрое решение систем типа Вандермонда, содержащих ортогональные многочлены». Журнал численного анализа IMA. 8 (4): 473–486. Дои:10.1093 / imanum / 8.4.473.
6. Björck, Å; В. Перейра (1970). «Решение систем уравнений Вандермонда». Математика вычислений. Американское математическое общество. 24 (112): 893–903. Дои:10.2307/2004623. JSTOR  2004623.
7. Кальветти, Д.; Райхель, Л. (1993). «Быстрое обращение матриц типа Вандермонда, содержащих ортогональные многочлены». КУСОЧЕК. 33 (33): 473–484. Дои:10.1007 / BF01990529.
8. Р. Бевилаква, Д. Бини, М. Каповани и О. Менчи (2003). Appunti di Calcolo Numerico. Глава 5, с. 89. Редакционная служба Университарио Пизы - Региональная Азиенда Диритто алло Студия Университарио.
9. Кубическая интерполяция не уникальна: эта модель, использующая сплайн Катмулла-Рома и базисные полиномы Лагранжа, проходит через все четыре точки. Примечание. В левой трети желтое расстояние по горизонтали отрицательное, поскольку черная точка находится слева от желтой точки; в правой трети зеленое расстояние по горизонтали отрицательное, поскольку черная точка находится справа от зеленой точки.
10. Бояджиев, Бояд (2012). "Близкие встречи с вторым числом Стирлинга" (PDF). Математика. Mag. 85: 252–266.
11. «Ошибки полиномиальной интерполяции» (PDF).
12. «Заметки о полиномиальной интерполяции» (PDF).
13. Уотсон (1980, п. 21) приписывает последний пример Бернштейн (1912).
14. Уотсон (1980, п. 21) относит эту теорему к Фабер (1914).
15. Крылов, В. И. (1956). "Сходимость алгебраического интерполирования покорням многочленов Чебышева для непрерывных функций и функций с ограниченным изменением" [Сходимость алгебраической интерполяции относительно корней полинома Чебышева для абсолютно непрерывных функций и функций ограниченной вариации]. Доклады Академии Наук СССР (Н.С.) (на русском). 107: 362–365. MR 18-32.

Рекомендации

• Бернштейн, Сергей Н. (1912). "Sur l'ordre de la meilleure приближение функций продолжается par les polynômes de degré donné" [О порядке наилучшего приближения непрерывных функций многочленами заданной степени]. Mem. Акад. Рой. Бельг. (На французском). 4: 1–104.
• Фабер, Георг (1914). "Über die interpolatorische Darstellung stetiger Funktionen" [Об интерполяции непрерывных функций]. Deutsche Math. Яр. (на немецком). 23: 192–210.
• Уотсон, Дж. Алистер (1980). Теория приближений и численные методы.. Джон Вили. ISBN  0-471-27706-1.

дальнейшее чтение

• Аткинсон, Кенделл А. (1988). "Глава 3.". Введение в численный анализ (2-е изд.). Джон Уайли и сыновья. ISBN  0-471-50023-2.
• Брутман, Л. (1997). «Функции Лебега для полиномиальной интерполяции - обзор». Анна. Нумер. Математика. 4: 111–127.
• Пауэлл, М. Дж. Д. (1981). "Глава 4". Теория и методы приближения. Издательство Кембриджского университета. ISBN  0-521-29514-9.
• Шацман, Мишель (2002). "Глава 4". Численный анализ: математическое введение. Оксфорд: Clarendon Press. ISBN  0-19-850279-6.
• Шюли, Эндре; Майерс, Дэвид (2003). "Глава 6". Введение в численный анализ. Издательство Кембриджского университета. ISBN  0-521-00794-1.

внешняя ссылка

• «Процесс интерполяции», Энциклопедия математики, EMS Press, 2001 [1994]
• АЛГЛИБ имеет реализации на C ++ / C #.
• GSL имеет полиномиальный интерполяционный код в C
• Демонстрация полиномиальной интерполяции.