Феномен Рунджеса - Runges phenomenon

Функция Рунге (красный, самый высокий центральный пик); интерполирующий полином 5-го порядка с равноотстоящими точками интерполяции (синий, нижний центральный пик); и интерполирующий полином 9-го порядка с равноотстоящими точками интерполяции (зеленый, средний центральный пик)

в математический поле числовой анализ, Феномен Рунге (Немецкий: [ˈʁʊŋə]) - проблема колебаний на краях интервала, возникающая при использовании полиномиальная интерполяция с многочленами высокой степени по набору равноотстоящих точек интерполяции. Это было обнаружено Карл Давид Толме Рунге (1901) при исследовании поведения ошибок при использовании полиномиальной интерполяции для приближения определенных функций.^[1]Открытие было важным, потому что оно показывает, что получение более высоких степеней не всегда улучшает точность. Явление похоже на Феномен Гиббса в приближении рядов Фурье.

Вступление

В Аппроксимационная теорема Вейерштрасса заявляет, что для каждого непрерывная функция ж(Икс), определенные на интервал [а,б] существует набор многочлен функции п_п(Икс) за п= 0, 1, 2,…, каждая степени не выше п, что приближает ж(Икс) с равномерное схождение над [а,б] в качестве п стремится к бесконечности, то есть

${\displaystyle \lim _{n\rightarrow \infty }\left(\max _{a\leq x\leq b}\left|f(x)-P_{n}(x)\right|\right)=0.}$

Рассмотрим случай, когда хочется интерполировать через п+1 точка функции через равные промежутки ж(Икс) с использованием п-степень полином п_п(Икс), который проходит через эти точки. Естественно, из теоремы Вейерштрасса можно было ожидать, что использование большего количества точек приведет к более точному восстановлению ж(Икс). Однако это частности набор полиномиальных функций п_п(Икс) свойство равномерной сходимости не гарантируется; теорема только утверждает, что существует набор полиномиальных функций, не обеспечивая общий метод поиска.

В п_п(Икс), произведенный таким образом, может фактически отличаться от ж(Икс) в качестве п увеличивается; обычно это происходит в виде колеблющегося шаблона, который увеличивается около концов точек интерполяции. Это явление приписывают Рунге.^[2]

Проблема

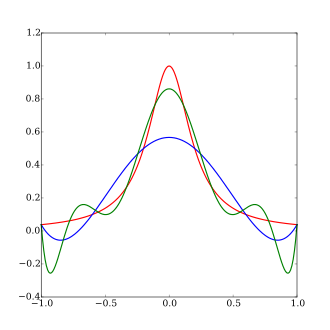
Рассмотрим Функция Рунге

${\displaystyle f(x)={\frac {1}{1+25x^{2}}}\,}$

(масштабная версия Ведьма Агнези Ранжем обнаружил, что если эта функция интерполированный в равноудаленных точках Икс_я от −1 до 1 такое, что:

${\displaystyle x_{i}={\frac {2i}{n}}-1,\quad i\in \left\{0,1,\dots ,n\right\}}$

с многочлен п_п(Икс) степени ≤п, результирующая интерполяция колеблется к концу интервала, то есть близко к -1 и 1. Можно даже доказать, что ошибка интерполяции увеличивается (неограниченно), когда степень полинома увеличивается:

${\displaystyle \lim _{n\rightarrow \infty }\left(\max _{-1\leq x\leq 1}|f(x)-P_{n}(x)|\right)=\infty .}$

Это показывает, что полиномиальная интерполяция высокой степени в равноотстоящих точках может быть проблематичной.

Причина

Феномен Рунге является следствием двух свойств этой проблемы.

• Величина п-го порядка этой функции быстро растет, когда п увеличивается.
• Эквидистантность между точками приводит к Постоянная Лебега что быстро увеличивается, когда п увеличивается.

Это явление графически очевидно, потому что оба свойства в совокупности увеличивают величину колебаний.

Ошибка между производящей функцией и интерполирующим полиномом порядка п дан кем-то

${\displaystyle f(x)-P_{n}(x)={\frac {f^{(n+1)}(\xi )}{(n+1)!}}\prod _{i=0}^{n}(x-x_{i})}$

для некоторых ${\displaystyle \xi }$ в (−1, 1). Таким образом,

${\displaystyle \max _{-1\leq x\leq 1}|f(x)-P_{n}(x)|\leq \max _{-1\leq x\leq 1}{\frac {\left|f^{(n+1)}(x)\right|}{(n+1)!}}\max _{-1\leq x\leq 1}\prod _{i=0}^{n}|x-x_{i}|}$.

Обозначим через ${\displaystyle w_{n}(x)}$ узловая функция

${\displaystyle w_{n}(x)=(x-x_{0})(x-x_{1})\cdots (x-x_{n})}$

и разреши ${\displaystyle W_{n}}$ быть максимумом величины ${\displaystyle w_{n}}$ функция:

${\displaystyle W_{n}=\max _{-1\leq x\leq 1}|w_{n}(x)|}$.

Элементарно доказать, что при равноудаленных узлах

${\displaystyle W_{n}\leq n!h^{n+1}}$

куда ${\displaystyle h=2/n}$ размер шага.

Кроме того, предположим, что (п+1) -я производная от ${\displaystyle f}$ ограничен, т.е.

${\displaystyle \max _{-1\leq x\leq 1}|f^{(n+1)}(x)|\leq M_{n+1}}$.

Следовательно,

${\displaystyle \max _{-1\leq x\leq 1}|f(x)-P_{n}(x)|\leq M_{n+1}{\frac {h^{n+1}}{(n+1)}}}$.

Но величина (п+1) -я производная функции Рунге возрастает при п увеличивается, поскольку ${\displaystyle M_{n+1}\leq (n+1)!5^{n+1}}$. Как следствие, полученная верхняя оценка ${\displaystyle (10/n)^{n+1}n!}$, стремится к бесконечности, когда п стремится к бесконечности.

Хотя это часто используется для объяснения феномена Рунге, тот факт, что верхняя граница ошибки уходит в бесконечность, не обязательно означает, конечно, что сама ошибка также расходится с п.

Смягчение проблемы

Изменение точек интерполяции

Колебания можно минимизировать, используя узлы, которые более плотно распределены по краям интервала, в частности, с асимптотической плотностью (на интервале [-1,1]), задаваемой формулой^[3]${\displaystyle 1/{\sqrt {1-x^{2}}}}$. Стандартный пример такого набора узлов: Чебышевские узлы, для которого максимальная ошибка аппроксимации функции Рунге гарантированно уменьшается с увеличением полиномиального порядка. Это явление демонстрирует, что полиномы высокой степени обычно не подходят для интерполяции с равноудаленными узлами.

Алгоритм S-Рунге без передискретизации

Когда необходимо использовать эквидистантные выборки, потому что повторная выборка на наборах узлов с хорошим поведением невозможна, можно рассмотреть алгоритм S-Рунге.^[4] В этом подходе исходный набор узлов отображается на набор Чебышевские узлы, обеспечивающий устойчивую полиномиальную реконструкцию. Особенность этого метода в том, что нет необходимости в передискретизации отображаемых узлов, которые также называются поддельные узлы. А Python реализацию этой процедуры можно найти здесь.

Использование кусочных полиномов

Проблему можно избежать, используя сплайновые кривые которые являются кусочно-полиномами. При попытке уменьшить ошибку интерполяции можно увеличить количество полиномиальных частей, которые используются для построения сплайна, вместо увеличения степени используемых полиномов.

Ограниченная минимизация

Можно также подобрать полином более высокой степени (например, с ${\displaystyle n}$ точки используют полином порядка ${\displaystyle N=n^{2}}$ вместо ${\displaystyle n+1}$), и подобрать интерполяционный полином, первая (или вторая) производная которого имеет минимальное ${\displaystyle L^{2}}$ норма.

Аналогичный подход заключается в минимизации ограниченной версии ${\displaystyle L^{p}}$ расстояние между полиномами ${\displaystyle m^{\mathrm {th} }}$ производная и среднее значение ее ${\displaystyle m^{\mathrm {th} }}$ производная. Явно, чтобы минимизировать

${\displaystyle V_{p}=\int _{a}^{b}\left|{\frac {\operatorname {d} ^{m}P_{N}(x)}{\operatorname {d} x^{m}}}-{\frac {1}{b-a}}\int _{a}^{b}{\frac {\operatorname {d} ^{m}P_{N}(z)}{\operatorname {d} z^{m}}}\operatorname {d} z\right|^{p}\operatorname {d} x-\sum _{i=1}^{n}\lambda _{i}\,\left(P_{N}(x_{i})-f(x_{i})\right),}$

куда ${\displaystyle N\geq n-1}$ и ${\displaystyle m<N}$, относительно полиномиальных коэффициентов и Множители Лагранжа, ${\displaystyle \lambda _{i}}$. Когда ${\displaystyle N=n-1}$, уравнения связи, порождаемые множителями Лагранжа, уменьшают ${\displaystyle P_{N}(x)}$ к минимальному многочлену, проходящему через все ${\displaystyle n}$ точки. На противоположном конце ${\displaystyle \lim _{N\rightarrow \infty }P_{N}(x)}$ приблизится к форме, очень похожей на приближение кусочно-полиномов. Когда ${\displaystyle m=1}$, особенно, ${\displaystyle \lim _{N\rightarrow \infty }P_{N}(x)}$ приближается к линейным кусочно-полиномам, т. е. соединяя точки интерполяции прямыми линиями.

Роль, которую играет ${\displaystyle p}$ в процессе минимизации ${\displaystyle V_{p}}$ состоит в том, чтобы контролировать важность размера отклонений от среднего значения. Чем больше ${\displaystyle p}$ то есть более сильные колебания наказываются по сравнению с небольшими. Наибольшее преимущество евклидовой нормы, ${\displaystyle p=2}$, заключается в том, что он допускает аналитические решения и гарантирует, что ${\displaystyle V_{p}}$ будет только один минимум. Когда ${\displaystyle p\neq 2}$ может быть несколько минимумов в ${\displaystyle V_{p}}$, что затрудняет обеспечение того, чтобы конкретный найденный минимум был глобальный минимум вместо местного.

Подгонка наименьших квадратов

Другой метод - подгонка полинома более низкой степени с использованием метода наименьших квадратов. Обычно при использовании ${\displaystyle m}$ равноудаленные точки, если ${\displaystyle N<2{\sqrt {m}}}$ тогда приближение наименьших квадратов ${\displaystyle P_{N}(x)}$ хорошо кондиционируется.^[5]

Полином Бернштейна

С помощью Многочлены Бернштейна, можно равномерно аппроксимировать каждую непрерывную функцию на отрезке, хотя этот метод довольно затратный в вычислительном отношении.^{[нужна цитата ]}

Связанные заявления от теория приближения

Для каждой предопределенной таблицы узлов интерполяции существует непрерывная функция, для которой последовательность полиномов интерполяции на этих узлах расходится.^[6] Для каждой непрерывной функции существует таблица узлов, на которых сходится процесс интерполяции.^{[нужна цитата ]} Чебышевская интерполяция (т.е. Чебышевские узлы ) сходится равномерно для любой абсолютно непрерывной функции.

Смотрите также

• Сравните с Феномен Гиббса для синусоидальных базисных функций
• Серия Тейлор
• Чебышевские узлы
• Теорема Стоуна – Вейерштрасса

Рекомендации

1. Рунге, Карл (1901), "Über empirische Funktionen und die Interpolation zwischen äquidistanten Ordinaten", Zeitschrift für Mathematik und Physik, 46: 224–243. доступны на www.archive.org
2. Эпперсон, Джеймс (1987). «На примере Рунге». Амер. Математика. Ежемесячно. 94: 329–341. Дои:10.2307/2323093.
3. Беррут, Жан-Поль; Trefethen, Ллойд Н. (2004), "Барицентрическая интерполяция Лагранжа", SIAM Обзор, 46 (3): 501–517, CiteSeerX  10.1.1.15.5097, Дои:10.1137 / S0036144502417715, ISSN  1095-7200
4. Де Марчи, Стефано; Маркетти, Франческо; Перраккионе, Эмма; Поджиали, Давиде (2020), «Полиномиальная интерполяция с помощью отображенных баз без повторной выборки», J. Comput. Appl. Математика., 364, Дои:10.1016 / j.cam.2019.112347, ISSN  0377-0427
5. Дальквист, Гермунд; Бьорк, Оке (1974), «4.3.4. Эквидистантная интерполяция и феномен Рунге», Численные методы, стр.101–103, ISBN  0-13-627315-7
6. Чейни, Уорд; Свет, Воля (2000), Курс теории приближений, Брукс / Коул, стр. 19, ISBN  0-534-36224-9