Преобразование Гильберта - Hilbert transform

В математика И в обработка сигналов, то Преобразование Гильберта это конкретный линейный оператор который принимает функцию, ты(т) реальной переменной и производит другую функцию реальной переменной ЧАС(ты)(т). Этот линейный оператор задается формулой свертка с функцией ${\displaystyle 1/(\pi t)}$:

${\displaystyle H(u)(t)={\frac {1}{\pi }}\int _{-\infty }^{\infty }{\frac {u(\tau )}{t-\tau }}\,d\tau ,}$

то несобственный интеграл понимается в основная стоимость смысл. Преобразование Гильберта имеет особенно простое представление в виде частотная область: Придает сдвиг фазы −90 ° на каждую фурье-компоненту функции. Например, преобразование Гильберта ${\displaystyle \cos(\omega t)}$, куда ω> 0, является ${\displaystyle \cos(\omega t-\pi /2)}$.

Преобразование Гильберта важно при обработке сигналов, поскольку оно позволяет получить аналитическое представление сигнала с действительным знаком ты(т). В частности, преобразование Гильберта ты это его гармоническое сопряжение v, функция действительной переменной т так что сложный -значная функция ты + я в допускает расширение комплекса верхняя полуплоскость удовлетворение Уравнения Коши – Римана. Преобразование Гильберта было впервые введено Дэвид Гильберт в этой настройке, чтобы решить частный случай Проблема Римана – Гильберта для аналитических функций.

Вступление

Преобразование Гильберта ты можно рассматривать как свертка из ты(т) с функцией час(т) = 1/ π т, известный как Ядро Коши. Потому что¹⁄_т не является интегрируемый через т = 0 , интеграл, определяющий свертку, не всегда сходится. Вместо этого преобразование Гильберта определяется с использованием Главное значение Коши (здесь обозначается p.v.). Явно преобразование Гильберта функции (или сигнала) ты(т) дан кем-то

${\displaystyle H(u)(t)={\frac {1}{\,\pi \,}}\,\operatorname {p.v.} \int _{-\infty }^{+\infty }{\frac {u(\tau )}{\;t-\tau \;}}\;\mathrm {d} \tau ~,}$

при условии, что этот интеграл существует как главное значение. Это как раз свертка ты с умеренное распределение p.v. 1/ π т (из-за Шварц (1950); видеть Панди (1996), Глава 3)). В качестве альтернативы, изменяя переменные, интеграл главного значения может быть записан явно (Зигмунд 1968, §XVI.1) ошибка harv: цель отсутствует: CITEREFZygmund1968 (помощь) в качестве

${\displaystyle H(u)(t)=-{\frac {1}{\,\pi \,}}\,\lim _{\varepsilon \to 0}\,\int _{\varepsilon }^{\infty }{\frac {\,u(t+\tau )-u(t-\tau )\,}{\tau }}\;\mathrm {d} \tau ~.}$

Когда преобразование Гильберта применяется дважды подряд к функции ты, результат отрицательный ты:

${\displaystyle H{\big (}\,H(u)\,{\big )}(t)=-u(t)~,}$

при условии, что интегралы, определяющие обе итерации, сходятся в подходящем смысле. В частности, обратное преобразование имеет вид −ЧАС . Этот факт легче всего увидеть, рассмотрев влияние преобразования Гильберта на преобразование Фурье ты(т) (видеть Связь с преобразованием Фурье, ниже).

Для аналитическая функция в верхняя полуплоскость, преобразование Гильберта описывает связь между действительной и мнимой частью граничных значений. То есть, если ж (z) аналитична в верхней полукомплексной плоскости {z : ℐ_м z > 0 } , и ты(т) = ℛ_е ж ( т + 0·я ) , тогда ℐ_м ж ( т + 0·я ) = ЧАС(ты)(т) с точностью до аддитивной константы, если существует это преобразование Гильберта.

Обозначение

В обработка сигналов преобразование Гильберта ты(т) обычно обозначается как ${\displaystyle {\hat {u}}(t)}$ (например., Брэндвуд 2003, п. 87 Ошибка harvnb: цель отсутствует: CITEREFBrandwood2003 (помощь)). Однако в математике это обозначение уже широко используется для обозначения преобразования Фурье ты(т) (например., Штайн и Вайс, 1971 г. ). Иногда преобразование Гильберта можно обозначить как ${\displaystyle {\tilde {u}}(t)}$. Кроме того, многие источники определяют преобразование Гильберта как отрицательное по сравнению с определенным здесь (например, Bracewell 2000, п. 359).

История

Преобразование Гильберта возникло в 1905 году в работе Гильберта над проблемой, поставленной Риманом относительно аналитических функций (Кресс (1989); Бицадзе (2001) Ошибка harvtxt: нет цели: CITEREFBitsadze2001 (помощь)), который стал известен как Проблема Римана – Гильберта. Работа Гильберта в основном была связана с преобразованием Гильберта для функций, определенных на окружности (Хведелидзе 2001 Ошибка harvnb: цель отсутствует: CITEREFKhvedelidze2001 (помощь); Гильберт 1953 ). Некоторые из его более ранних работ, связанных с дискретным преобразованием Гильберта, восходят к лекциям, которые он читал. Гёттинген. Результаты были позже опубликованы Германом Вейлем в его диссертации (Харди, Литтлвуд и Поля 1952, §9.1). Шур улучшил результаты Гильберта о дискретном преобразовании Гильберта и распространил их на интегральный случай (Харди, Литтлвуд и Поля 1952, §9.2). Эти результаты были ограничены пространствами L² и ℓ². В 1928 г. Марсель Рис доказал, что преобразование Гильберта можно определить для ты в L ^п(ℝ) за 1 < п < ∞ , что преобразование Гильберта является ограниченный оператор на L ^п(ℝ) за 1 < п < ∞ , и что аналогичные результаты верны для преобразования Гильберта на окружности, а также для дискретного преобразования Гильберта (Рис 1928 ). Преобразование Гильберта было вдохновляющим примером для Антони Зигмунд и Альберто Кальдерон во время изучения сингулярные интегралы (Кальдерон и Зигмунд 1952 ). Их исследования сыграли фундаментальную роль в современном гармоническом анализе. Различные обобщения преобразования Гильберта, такие как билинейные и трилинейные преобразования Гильберта, все еще являются активными областями исследований сегодня.

Связь с преобразованием Фурье

Преобразование Гильберта - это оператор множителя (Duoandikoetxea 2000, Глава 3). Множитель ЧАС является σ_ЧАС(ω) = −я sgn (ω) , куда sgn это сигнум функция. Следовательно:

${\displaystyle {\mathcal {F}}{\bigl (}H(u){\bigr )}(\omega )=-i\operatorname {sgn}(\omega )\cdot {\mathcal {F}}(u)(\omega )~,}$

куда ${\displaystyle {\mathcal {F}}}$ обозначает преобразование Фурье. С sgn (Икс) = sgn (2πИкс) , следует, что этот результат применим к трем общим определениям ${\displaystyle {\mathcal {F}}}$.

К Формула Эйлера,

${\displaystyle \sigma _{H}(\omega )={\begin{cases}~~i=e^{+{\frac {i\pi }{2}}},&{\text{for }}\omega <0,\\~~0,&{\text{for }}\omega =0,\\-i=e^{-{\frac {i\pi }{2}}},&{\text{for }}\omega >0.\end{cases}}}$

Следовательно, ЧАС(ты)(т) имеет эффект сдвига фазы отрицательная частота компоненты ты(т) на + 90 ° (^π⁄₂ радиан) и фазу положительных частотных составляющих на −90 °. И я·ЧАС(ты)(т) имеет эффект восстановления положительных частотных составляющих при сдвиге отрицательных частотных составляющих еще на + 90 °, что приводит к их отрицанию (то есть умножению на -1).

Когда преобразование Гильберта применяется дважды, фаза отрицательной и положительной частотных составляющих ты(т) сдвинуты соответственно на + 180 ° и -180 °, что эквивалентно. Сигнал отменен; т.е. ЧАС(ЧАС(ты)) = −ты , потому что

${\displaystyle {\bigl (}\sigma _{H}(\omega ){\bigr )}^{2}=e^{\pm i\pi }=-1\quad {\text{for }}\omega \neq 0~.}$

Таблица избранных преобразований Гильберта

В следующей таблице частота параметр ${\displaystyle \omega }$ реально.

Сигнал ${\displaystyle \,u(t)\,}$	Преобразование Гильберта[fn 1] ${\displaystyle \,H(u)(t)\,}$
${\displaystyle \sin(\omega t)}$ [fn 2]	${\displaystyle \operatorname {sgn}(\omega )\sin \left(\omega t-{\tfrac {\pi }{2}}\right)=-\operatorname {sgn}(\omega )\cos(\omega t)}$
${\displaystyle \cos(\omega t)}$ [fn 2]	${\displaystyle {\begin{aligned}\operatorname {sgn}(\omega )\cos \left(\omega t-{\tfrac {\pi }{2}}\right)&=\operatorname {sgn}(\omega )\sin(\omega t)\\&=\sin(|\omega |t)\end{aligned}}}$
${\displaystyle e^{i\omega t}}$	${\displaystyle \operatorname {sgn}(\omega )e^{i\left(\omega t-{\tfrac {\pi }{2}}\right)}=-i\cdot \operatorname {sgn}(\omega )e^{i\omega t}}$
${\displaystyle 1 \over t^{2}+1}$	${\displaystyle t \over t^{2}+1}$
${\displaystyle e^{-t^{2}}}$	${\displaystyle {\frac {2}{\sqrt {\pi \,}}}F(t)}$ (видеть Функция Доусона )
Функция Sinc ${\displaystyle \sin(t) \over t}$	${\displaystyle 1-\cos(t) \over t}$
Прямоугольная функция ${\displaystyle \sqcap (t)}$	${\displaystyle {1 \over \pi }\ln \left\vert {t+{1 \over 2} \over t-{1 \over 2}}\right\vert }$
Дельта-функция Дирака ${\displaystyle \delta (t)}$	${\displaystyle {1 \over \pi t}}$
Характеристика Функция ${\displaystyle \chi _{[a,b]}(t)}$	${\displaystyle {{\frac {1}{\pi }}\ln \left\vert {\frac {t-a}{t-b}}\right\vert }}$

Примечания

1. Некоторые авторы (например, Брейсвелл) используют наш -ЧАС как их определение прямого преобразования. Как следствие, правая колонка этой таблицы будет инвертирована.
2. Преобразование Гильберта функций sin и cos можно определить, взяв главное значение интеграла на бесконечности. Это определение согласуется с результатом определения преобразования Гильберта по распределению.

Доступна обширная таблица преобразований Гильберта (Король 2009b Отметим, что преобразование Гильберта константы равно нулю.

Область определения

Ни в коем случае не очевидно, что преобразование Гильберта вообще правильно определено, поскольку определяющий его несобственный интеграл должен сходиться в подходящем смысле. Однако преобразование Гильберта хорошо определено для широкого класса функций, а именно для функций из L ^п(ℝ) за 1 < п < ∞ .

Точнее, если ты в L ^п(ℝ) за 1 < п < ∞ , то предел, определяющий несобственный интеграл

${\displaystyle H(u)(t)=-{\frac {1}{\pi }}\lim _{\varepsilon \rightarrow 0}\int _{\epsilon }^{\infty }{\frac {u(t+\tau )-u(t-\tau )}{\tau }}\,d\tau }$

существует для почти каждый т . Функция предела также находится в L ^п(ℝ) и фактически также является пределом в среднем несобственного интеграла. То есть,

${\displaystyle -{\frac {1}{\pi }}\int _{\epsilon }^{\infty }{\frac {u(t+\tau )-u(t-\tau )}{\tau }}\,d\tau \to H(u)(t)}$

в качестве ε → 0 в L ^п норме, а также поточечно почти всюду Теорема Титчмарша (Титчмарш 1948, Глава 5) ошибка harv: цель отсутствует: CITEREFTitchmarsh1948 (помощь).

В случае L = 1 преобразование Гильберта по-прежнему сходится поточечно почти всюду, но само может не быть интегрируемым даже локально (Титчмарш 1948, §5.14) ошибка harv: цель отсутствует: CITEREFTitchmarsh1948 (помощь). В частности, сходимости в среднем в этом случае вообще не происходит. Преобразование Гильберта L¹ функция сходится, однако, в L¹-слабым, а преобразование Гильберта является ограниченным оператором из L¹ к L^{1, Вт} (Штайн и Вайс, 1971 г., Лемма V.2.8). (В частности, поскольку преобразование Гильберта также является оператором множителя на L², Интерполяция Марцинкевича и аргумент двойственности предоставляет альтернативное доказательство того, что ЧАС ограничен L ^п.)

Характеристики

Ограниченность

Если 1 < п < ∞ , то преобразование Гильберта на L ^п(ℝ) это ограниченный линейный оператор, что означает, что существует постоянная C_п такой, что

${\displaystyle \|Hu\|_{p}\leq C_{p}\|u\|_{p}}$

для всех ты ∈ L ^п(ℝ) . Эта теорема связана с Рисс (1928 г., VII); смотрите также Титчмарш (1948, Теорема 101) Ошибка harvtxt: нет цели: CITEREFTitchmarsh1948 (помощь).

Лучшая константа ${\displaystyle C_{p}}$ дан кем-то

${\displaystyle C_{p}={\begin{cases}\tan {\frac {\pi }{2p}}&{\text{ for }}1<p\leq 2\\\cot {\frac {\pi }{2p}}&{\text{ for }}2<p<\infty \end{cases}}}$

Этот результат обусловлен (Пихориды 1972 ); смотрите также Графакос (2004 г., Замечание 4.1.8). Простой способ найти лучшее ${\displaystyle C_{p}}$ за ${\displaystyle p}$ степень двойки обусловлена ​​так называемой идентичностью Котлара, которая ${\displaystyle (Hf)^{2}=f^{2}+2H(fHf)}$ для всех действительных f. Те же самые лучшие константы верны для периодического преобразования Гильберта.

Из ограниченности преобразования Гильберта следует L ^п(ℝ) сходимость симметричного оператора частичной суммы

${\displaystyle S_{R}f=\int _{-R}^{R}{\hat {f}}(\xi )e^{2\pi ix\xi }\,d\xi }$

к ж в L ^п(ℝ)см. например (Duoandikoetxea 2000, п. 59).

Антисамосопряженность

Преобразование Гильберта является анти-самосопряженный оператор относительно двойственности пары между L ^п(ℝ) и двойное пространство L^q(ℝ), куда п и q находятся Конъюгаты Гёльдера и 1 < п, q < ∞ . Символично,

${\displaystyle \langle Hu,v\rangle =\langle u,-Hv\rangle }$

за ты ∈ L ^п(ℝ) и v ∈ L^q(ℝ)(Титчмарш 1948, Теорема 102) ошибка harv: цель отсутствует: CITEREFTitchmarsh1948 (помощь).

Обратное преобразование

Преобразование Гильберта - это антиинволюция (Титчмарш 1948, п. 120) ошибка harv: цель отсутствует: CITEREFTitchmarsh1948 (помощь), означающий, что

${\displaystyle H(H(u))=-u}$

при условии, что каждое преобразование четко определено. С ЧАС сохраняет пространство L ^п(ℝ), из этого, в частности, следует обратимость преобразования Гильберта на L ^п(ℝ), и это

${\displaystyle H^{-1}=-H}$

Сложная структура

Потому что   ЧАС² = −Ⅰ   (“ Ⅰ " это оператор идентификации ) на реальном Банахово пространство из настоящий-значные функции в L ^п(ℝ)преобразование Гильберта определяет линейная сложная структура на этом банаховом пространстве. В частности, когда   п = 2 ,   преобразование Гильберта дает гильбертово пространство действительных функций в L²(ℝ) структура сложный Гильбертово пространство.

Комплекс) собственные состояния преобразования Гильберта допускают представления в виде голоморфные функции в верхней и нижней полуплоскостях в Харди космос ЧАС² посредством Теорема Пэли – Винера..

Дифференциация

Формально производная преобразования Гильберта является преобразованием Гильберта производной, то есть эти два линейных оператора коммутируют:

${\displaystyle H\left({\frac {du}{dt}}\right)={\frac {d}{dt}}H(u)}$

Повторяя эту личность,

${\displaystyle H\left({\frac {d^{k}u}{dt^{k}}}\right)={\frac {d^{k}}{dt^{k}}}H(u)}$

Это строго верно, как указано при условии ты и его первый k производные принадлежат L ^п(ℝ) (Панди 1996, §3.3). Это легко проверить в частотной области, где дифференцирование превращается в умножение на ω.

Свертки

Преобразование Гильберта формально можно реализовать как свертка с умеренное распределение (Duistermaat & Kolk 2010, п. 211)

${\displaystyle h(t)=\operatorname {p.v.} {\frac {1}{\;\pi \,t\;}}}$

Таким образом, формально

${\displaystyle H(u)=h*u}$

Тем не мение, априори это может быть определено только для ты распределение компактная опора. С этим можно работать несколько строго, поскольку функции с компактным носителем (которые являются распределениями a fortiori) находятся плотный в L ^п . В качестве альтернативы можно использовать тот факт, что час(т) это производная по распределению функции бревно остроумие

${\displaystyle H(u)(t)={\frac {d}{dt}}\left({\frac {1}{\,\pi \,}}(u*\log |\cdot |)(t)\right)}$

Для большинства операционных целей преобразование Гильберта можно рассматривать как свертку. Например, в формальном смысле преобразование Гильберта свертки - это свертка преобразования Гильберта, примененного к только один любого из факторов:

${\displaystyle H(u*v)=H(u)*v=u*H(v)}$

Это строго верно, если ты и v являются распределениями с компактным носителем, поскольку в этом случае

${\displaystyle h*(u*v)=(h*u)*v=u*(h*v)}$

Таким образом, переходя к соответствующему пределу, это также верно, если   ты ∈ L ^п   и   v ∈ L^q   при условии, что

${\displaystyle 1<{\frac {1}{\,p\,}}+{\frac {1}{\,q\,}}}$

из теоремы в силу Титчмарш (1948, Теорема 104) Ошибка harvtxt: нет цели: CITEREFTitchmarsh1948 (помощь).

Инвариантность

Преобразование Гильберта обладает следующими свойствами инвариантности на L²(ℝ).

• Он общается с переводчиками. То есть коммутирует с операторами Т_а ж (Икс) = ж (Икс + а) для всех а в ℝ.
• Он коммутирует с положительными расширениями. То есть коммутирует с операторами M_λ ж (Икс) = ж (λ x) для всех λ > 0 .
• Это антикоммуты с отражением R f (Икс) = ж (-X) .

С точностью до мультипликативной константы преобразование Гильберта является единственным ограниченным оператором на L² с этими свойствами (Штейн 1970, §III.1).

На самом деле существует более широкий набор операторов, которые коммутируют с преобразованием Гильберта. Группа SL (2, ℝ) действует унитарными операторами U_грамм на пространстве L²(ℝ) по формуле

${\displaystyle \operatorname {U} _{g}^{-1}f(x)={\frac {1}{\,cx+d\,}}\,f\left({\frac {ax+b}{cx+d}}\right)\,,\qquad g={\begin{bmatrix}a&b\\c&d\end{bmatrix}}\,,\qquad {\text{ for }}~ad-bc=\pm 1~.}$

Этот унитарное представительство является примером представление основной серии из SL (2, ℝ). В этом случае оно приводимо, разбиваясь как ортогональная сумма двух инвариантных подпространств, Харди космос ЧАС²(ℝ) и его сопряженный. Это пространства L² граничные значения голоморфных функций на верхней и нижней полуплоскостях. ЧАС²(ℝ) и его сопряжение состоит именно из тех L² функции с преобразованием Фурье, исчезающим на отрицательной и положительной частях вещественной оси соответственно. Поскольку преобразование Гильберта равно ЧАС = −я (2п − Ⅰ) , с п ортогональная проекция из L²(ℝ) на ЧАС²(ℝ), и Ⅰ то оператор идентификации, следует, что ЧАС²(ℝ) а его ортогональные - собственные подпространства ЧАС для собственных значений ±я. Другими словами, ЧАС коммутирует с операторами U_грамм. Ограничения операторов U_грамм к ЧАС²(ℝ) и его сопряженные дают неприводимые представления SL (2, ℝ) - так называемой предел представлений дискретной серии.^[1]

Расширение области определения

Преобразование Гильберта распределений

Кроме того, можно распространить преобразование Гильберта на некоторые пространства распределения (Панди 1996, Глава 3). Поскольку преобразование Гильберта коммутирует с дифференцированием и является ограниченным оператором на L ^п, ЧАС ограничивает непрерывное преобразование обратный предел из Соболевские пространства:

${\displaystyle {\mathcal {D}}_{L^{p}}={\underset {n\to \infty }{\underset {\longleftarrow }{\lim }}}W^{n,p}(\mathbb {R} )}$

Тогда преобразование Гильберта можно определить на двойственном пространстве к ${\displaystyle {\mathcal {D}}_{L^{p}}}$, обозначенный ${\displaystyle {\mathcal {D}}_{L^{p}}'}$, состоящий из L ^п раздачи. Это достигается за счет спаривания дуальности:
За ${\displaystyle u\in {\mathcal {D}}'_{L^{p}}}$, определять:

${\displaystyle H(u)\in {\mathcal {D}}'_{L^{p}}=\langle Hu,v\rangle \ \triangleq \ \langle u,-Hv\rangle ,\ {\text{for all}}\ v\in {\mathcal {D}}_{L^{p}}.}$

Можно определить преобразование Гильберта на пространстве умеренные распределения а также подходом из-за Гельфанд и Шилов (1968), но требуется гораздо больше осторожности из-за особенности в интеграле.

Преобразование Гильберта ограниченных функций

Преобразование Гильберта можно определить для функций из L^∞(ℝ) также, но это требует некоторых изменений и оговорок. При правильном понимании преобразование Гильберта отображает L^∞(ℝ) к Банахово пространство из ограниченное среднее колебание (BMO) классы.

Наивно интерпретируемое преобразование Гильберта ограниченной функции явно неверно определено. Например, с ты = sgn (Икс), интеграл, определяющий ЧАС(ты) расходится почти везде, чтобы ±∞. Чтобы облегчить такие трудности, преобразование Гильберта L^∞ функция поэтому определяется следующим упорядоченный форма интеграла

${\displaystyle H(u)(t)=\operatorname {p.v.} \int _{-\infty }^{\infty }u(\tau )\left\{h(t-\tau )-h_{0}(-\tau )\right\}\,d\tau }$

где как указано выше час(Икс) = 1/ π Икс  и

${\displaystyle h_{0}(x)={\begin{cases}0&{\text{ for }}~|x|<1\\{\frac {1}{\,\pi \,x\,}}&{\text{ for }}~|x|\geq 1\end{cases}}}$

Модифицированное преобразование ЧАС согласуется с исходным преобразованием функций компактного носителя из общего результата Кальдерон и Зигмунд (1952); видеть Фефферман (1971). Кроме того, полученный интеграл поточечно сходится почти всюду и относительно нормы BMO к функции ограниченного среднего колебания.

А глубокий результат из Фефферман (1971) и Фефферман и Штейн (1972) состоит в том, что функция имеет ограниченное среднее колебание тогда и только тогда, когда она имеет вид ж + ЧАС(грамм) для некоторых ж, грамм ∈ L^∞(ℝ) .

Сопряженные функции

Преобразование Гильберта можно понять в терминах пары функций ж (Икс) и грамм(Икс) так что функция

${\displaystyle F(x)=f(x)+i\,g(x)}$

граничное значение голоморфная функция F(z) в верхней полуплоскости (Титчмарш 1948, Глава V) ошибка harv: цель отсутствует: CITEREFTitchmarsh1948 (помощь). В этих условиях, если ж и грамм достаточно интегрируемы, то одно является преобразованием Гильберта другого.

Предположим, что ж ∈ L ^п(ℝ) . Тогда по теории Интеграл Пуассона, ж допускает единственное гармоническое продолжение в верхнюю полуплоскость, и это продолжение дается формулой

${\displaystyle u(x+iy)=u(x,y)={\frac {1}{\,\pi \,}}\int _{-\infty }^{\infty }f(s)\;{\frac {y}{(x-s)^{2}+y^{2}}}\;ds}$

что является сверткой ж с Ядро Пуассона

${\displaystyle P(x,y)={\frac {y}{\,\pi \,(x^{2}+y^{2})\,}}}$

Кроме того, существует уникальная гармоническая функция v определенная в верхней полуплоскости такая, что F(z) = ты(z) + я в(z) голоморфен и

${\displaystyle \lim _{y\to \infty }v\,(x+i\,y)=0}$

Эта гармоническая функция получается из ж взяв свертку с сопряженное ядро ​​Пуассона

${\displaystyle Q(x,y)={\frac {x}{\,\pi \,(x^{2}+y^{2})\,}}~.}$

Таким образом

${\displaystyle v(x,y)={\frac {1}{\pi }}\int _{-\infty }^{\infty }f(s)\;{\frac {x-s}{\,(x-s)^{2}+y^{2}\,}}\;ds}$

Действительно, действительная и мнимая части ядра Коши равны

${\displaystyle {\frac {i}{\,\pi \,z\,}}=P(x,y)+i\,Q(x,y)}$

так что F = ты + я в голоморфен Интегральная формула Коши.

Функция v получен из ты таким образом называется гармоническое сопряжение из ты. Граничный (не касательный) предел v(Икс,у) в качестве у → 0 преобразование Гильберта ж. Таким образом, кратко,

${\displaystyle H(f)=\lim _{y\to 0}Q(-,y)\star f}$

Теорема Титчмарша

Теорема Титчмарша (названная в честь E.C. Титчмарш включивший его в свою работу 1937 г.) уточняет связь между граничными значениями голоморфных функций в верхней полуплоскости и преобразованием Гильберта (Титчмарш 1948, Теорема 95) ошибка harv: цель отсутствует: CITEREFTitchmarsh1948 (помощь). Он дает необходимые и достаточные условия для комплекснозначного интегрируемый с квадратом функция F(Икс) на действительной прямой как граничное значение функции в Харди космос ЧАС²(U) голоморфных функций в верхней полуплоскости U.

Теорема утверждает, что следующие условия для комплекснозначной квадратично интегрируемой функции F : ℝ → ℂ эквивалентны:

• F(Икс) это предел как z → Икс голоморфной функции F(z) в верхней полуплоскости такая, что

${\displaystyle \int _{-\infty }^{\infty }|F(x+i\,y)|^{2}\;dx<K}$

• Реальная и мнимая части F(Икс) являются преобразованиями Гильберта друг друга.
• В преобразование Фурье ${\displaystyle {\mathcal {F}}(F)(x)}$ исчезает для Икс < 0 .

Более слабый результат верен для функций класса L ^п за п > 1 (Титчмарш 1948, Теорема 103) ошибка harv: цель отсутствует: CITEREFTitchmarsh1948 (помощь). В частности, если F(z) голоморфная функция такая, что

${\displaystyle \int _{-\infty }^{\infty }|F(x+i\,y)|^{p}\;dx<K}$

для всех у, то существует комплексная функция F(Икс) в L ^п(ℝ) такой, что F(Икс + я у) → F(Икс) в L ^п норма как у → 0 (а также удерживая точечно почти всюду ). Более того,

${\displaystyle F(x)=f(x)-i\,g(x)}$

куда ж является вещественной функцией в L ^п(ℝ) и грамм - преобразование Гильберта (класса L ^п) из ж.

Это не так в случае п = 1 . Фактически, преобразование Гильберта L¹ функция ж не обязательно сходиться в среднем к другому L¹ функция. Тем не менее, (Титчмарш 1948, Теорема 105) ошибка harv: цель отсутствует: CITEREFTitchmarsh1948 (помощь)преобразование Гильберта ж сходится почти всюду к конечной функции грамм такой, что

${\displaystyle \int _{-\infty }^{\infty }{\frac {\;|g(x)|^{p}\,}{\;1+x^{2}\;}}\;dx<\infty }$

Этот результат прямо аналогичен результату Андрей Колмогоров для функций Харди на диске (Дюрен 1970, Теорема 4.2). Хотя этот результат обычно называют теоремой Титчмарша, результат объединяет многие работы других авторов, в том числе Харди, Пэли и Винера (см. Теорема Пэли – Винера. ), а также работы Рисса, Хилле и Тамаркина (см. раздел 4.22 в Король (2009a) ).

Проблема Римана – Гильберта

Одна форма Проблема Римана – Гильберта стремится идентифицировать пары функций F₊ и F₋ такой, что F₊ является голоморфный в верхней полуплоскости и F₋ голоморфна в нижней полуплоскости, так что при Икс вдоль действительной оси,

${\displaystyle F_{+}(x)-F_{-}(x)=f(x)}$

куда ж (Икс) некоторая заданная действительная функция от Икс ∈ ℝ . Левую часть этого уравнения можно понимать либо как разность пределов F_± из соответствующих полуплоскостей или как гиперфункция распределение. Две функции этого вида являются решением проблемы Римана – Гильберта.

Формально, если F_± решить проблему Римана – Гильберта

${\displaystyle f(x)=F_{+}(x)-F_{-}(x)}$

то преобразование Гильберта ж (Икс) дан кем-то

${\displaystyle H(f)(x)=-i{\Bigl (}F_{+}(x)+F_{-}(x){\Bigr )}~}$ (Панди 1996, Глава 2).

Преобразование Гильберта на окружности

Смотрите также: Харди космос

Для периодической функции ж определяется круговое преобразование Гильберта:

${\displaystyle {\tilde {f}}(x)\triangleq {\frac {1}{\,2\pi \,}}\operatorname {p.v.} \int _{0}^{2\pi }f(t)\,\cot \left({\frac {\,x-t\,}{2}}\right)\,dt}$

Круговое преобразование Гильберта используется при описании пространства Харди и при изучении сопряженной функции в рядах Фурье. Ядро,

${\displaystyle \cot \left({\frac {\,x-t\,}{2}}\right)}$

известен как Ядро Гильберта поскольку именно в этой форме преобразование Гильберта было первоначально изучено (Хведелидзе 2001 ) ошибка harv: цель отсутствует: CITEREFKhvedelidze2001 (помощь).

Ядро Гильберта (для кругового преобразования Гильберта) можно получить, сделав ядро ​​Коши¹⁄_Икс периодический. Точнее, для Икс ≠ 0

${\displaystyle {\frac {1}{\,2\,}}\cot \left({\frac {\,x\,}{2}}\right)={\frac {1}{\,x\,}}+\sum _{n=1}^{\infty }\left({\frac {1}{\,x+2n\pi \,}}+{\frac {1}{\,x-2n\pi \,}}\right)}$

Многие результаты о круговом преобразовании Гильберта могут быть получены из соответствующих результатов для преобразования Гильберта из этого соответствия.

Еще одна более прямая связь обеспечивается преобразованием Кэли C(Икс) = ( Икс – я ) / ( Икс + я ) , который переносит действительную прямую на окружность и верхнюю полуплоскость на единичный диск. Он индуцирует унитарное отображение

${\displaystyle U\,f(x)={\frac {1}{\;(x+i)\,{\sqrt {\pi \;}}\,}}\,f\left(\,C\left(x\right)\,\right)}$

из L²(Т) на L²(ℝ). Оператор U несет пространство Харди ЧАС²(Т) на пространство Харди ЧАС²(ℝ).^[2]

Преобразование Гильберта в обработке сигналов

Теорема Бедросяна

Теорема Бедросяна утверждает, что преобразование Гильберта продукта сигнала нижних частот и сигналов верхних частот с неперекрывающимися спектрами задается произведением сигнала нижних частот и преобразования Гильберта сигнала верхних частот, или

${\displaystyle H(f_{LP}(t)f_{HP}(t))=f_{LP}(t)H(f_{HP}(t))}$

куда ж_LP и ж_HP - сигналы нижних и верхних частот соответственно (Schreier & Scharf 2010, 14).

Сигналы с амплитудной модуляцией моделируются как продукт ограниченный диапазон форма волны "сообщения", ты_м(т), и синусоидальный «носитель»:

${\displaystyle u(t)=u_{m}(t)\cdot \cos(\omega t+\phi )}$

Когда ты_м(т) не имеет частотного содержания выше несущей частоты, ${\displaystyle {\frac {\omega }{2\pi }}{\text{ Hz }},}$ затем по теореме Бедросяна:

${\displaystyle H(u)(t)=u_{m}(t)\cdot \sin(\omega t+\phi )}$ (Бедросян 1962 )

Аналитическое представление

Основная статья: аналитический сигнал

В контексте обработки сигналов интерпретация сопряженной функции преобразования Гильберта, обсужденная выше, дает аналитическое представление сигнала ты(т):

${\displaystyle u_{a}(t)=u(t)+i\cdot H(u)(t)}$

который является голоморфная функция в верхней полуплоскости.

Для узкополосной модели (см. Выше) аналитическое представление:

${\displaystyle {\begin{aligned}u_{a}(t)&=u_{m}(t)\cdot \cos(\omega t+\phi )+i\cdot u_{m}(t)\cdot \sin(\omega t+\phi )\\&=u_{m}(t)\cdot \left[\cos(\omega t+\phi )+i\cdot \sin(\omega t+\phi )\right]\end{aligned}}}$

${\displaystyle =u_{m}(t)\cdot e^{i(\omega t+\phi )}\,}$ (к Формула Эйлера )

(Уравнение 1)

Этот комплекс гетеродин операция сдвигает все частотные составляющие ты_м(т) выше 0 Гц. В этом случае мнимая часть результата является преобразованием Гильберта действительной части. Это косвенный способ получения преобразований Гильберта.

Угловая (фазовая / частотная) модуляция

Форма:

${\displaystyle u(t)=A\cdot \cos(\omega t+\phi _{m}(t))}$

называется угловая модуляция, который включает как фазовая модуляция и модуляция частоты. В мгновенная частота является${\displaystyle \omega +\phi _{m}^{\prime }(t).}$ Для достаточно больших ω, в сравнении с ${\displaystyle \,\phi _{m}^{\prime }\,}$:

${\displaystyle H(u)(t)\approx A\cdot \sin(\omega t+\phi _{m}(t))}$

и:

${\displaystyle u_{a}(t)\approx A\cdot e^{i(\omega t+\phi _{m}(t))}}$

Модуляция с одной боковой полосой (SSB)

Основная статья: Однополосная модуляция

Когда ты_м(т) вУравнение 1 является также аналитическое представление (формы волны сообщения), то есть:

${\displaystyle u_{m}(t)=m(t)+i\cdot {\widehat {m}}(t)}$

результат односторонняя полоса модуляция:

${\displaystyle u_{a}(t)=(m(t)+i\cdot {\widehat {m}}(t))\cdot e^{i(\omega t+\phi )}}$

переданный компонент которого:

${\displaystyle {\begin{aligned}u(t)&=\operatorname {Re} \{u_{a}(t)\}\\&=m(t)\cdot \cos(\omega t+\phi )-{\widehat {m}}(t)\cdot \sin(\omega t+\phi )\end{aligned}}}$

Причинно-следственная связь

Функция час с час(т) = 1/ π т это беспричинный фильтр и поэтому не может быть реализован как есть, когда ты сигнал, зависящий от времени. Если ты является функцией вневременной переменной (например, пространственной), отсутствие причинности может не быть проблемой. Фильтр тоже бесконечный поддерживать, что может быть проблемой в некоторых приложениях. Другая проблема связана с тем, что происходит с нулевой частотой (DC), чего можно избежать, если s не содержит DC-компонента.

Практическая реализация во многих случаях подразумевает, что для аппроксимации вычислений используется фильтр с конечной поддержкой, который, кроме того, становится причинным с помощью подходящей задержки. Приближение также может означать, что только определенный частотный диапазон подвержен характерному фазовому сдвигу, связанному с преобразованием Гильберта. Смотрите также квадратурный фильтр.

Дискретное преобразование Гильберта

Рисунок 1: Фильтр, частотная характеристика которого ограничена примерно до 95% частоты Найквиста.

фигура 2: Фильтр преобразования Гильберта с высокочастотной характеристикой

Рисунок 3.

Рисунок 4. Преобразование Гильберта cos (ωt) является грех (ωt). Этот рисунок показывает грех (ωt) и два приближенных преобразования Гильберта, вычисленные библиотечной функцией MATLAB, hilbert (·)

Рисунок 5. Дискретные преобразования Гильберта косинусной функции с использованием кусочной свертки

Для дискретной функции ${\displaystyle \,u[n]\,,}$ с преобразование Фурье с дискретным временем (DTFT), ${\displaystyle \,U(\omega )\,,}$ и дискретное преобразование Гильберта ${\displaystyle \,{\hat {u}}[n]\,,}$ ДВПФ ${\displaystyle \,{\hat {u}}[n]\,}$ в регионе −π <ω < π дан кем-то:

${\displaystyle \operatorname {DTFT} \displaystyle ({\hat {u}})=U(\omega )\cdot (-i\cdot \operatorname {sgn}(\omega )).}$

Обратный ДВПФ с использованием теорема свертки, является:

${\displaystyle {\begin{aligned}{\hat {u}}[n]&=\scriptstyle {\mathrm {DTFT} }^{-1}\displaystyle (U(\omega ))\ *\ \scriptstyle {\mathrm {DTFT} }^{-1}\displaystyle (-i\cdot \operatorname {sgn}(\omega ))\\&=u[n]\ *\ {\frac {1}{2\pi }}\int _{-\pi }^{\pi }(-i\cdot \operatorname {sgn}(\omega ))\cdot e^{i\omega n}\,d\omega \\&=u[n]\ *\ \underbrace {{\frac {1}{2\pi }}\left[\int _{-\pi }^{0}i\cdot e^{i\omega n}\,d\omega -\int _{0}^{\pi }i\cdot e^{i\omega n}\,d\omega \right]} _{h[n]},\end{aligned}}}$

куда

${\displaystyle h[n]\ \triangleq \ {\begin{cases}0,&{\text{for }}n{\text{ even}}\\{\frac {2}{\pi n}}&{\text{for }}n{\text{ odd}},\end{cases}}}$

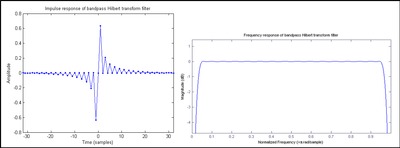
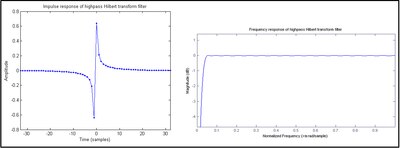
который представляет собой бесконечную импульсную характеристику (БИХ). Когда свертка выполняется численно, FIR приближение заменяется на час[п], как показано в Рисунок 1. КИХ-фильтр с нечетным числом антисимметричных коэффициентов называется типом III, который по своей природе демонстрирует отклики нулевой величины на частотах 0 и Найквиста, что в данном случае приводит к форме полосового фильтра. Схема типа IV (четное число антисимметричных коэффициентов) показана на фигура 2. Поскольку амплитудная характеристика на частоте Найквиста не пропадает, он немного лучше приближает идеальный преобразователь Гильберта, чем фильтр с нечетным ответвлением. тем не мение

• Типичный (т.е. правильно отфильтрованный и отобранный) ты[п] последовательность не имеет полезных компонентов на частоте Найквиста.
• Для импульсной характеристики IV типа требуется¹⁄₂ сдвиг образца в час[п] последовательность. Это приводит к тому, что коэффициенты с нулевым значением становятся ненулевыми, как показано на фигура 2. Таким образом, конструкция типа III потенциально вдвое эффективнее, чем тип IV.
• Групповая задержка конструкции типа III - это целое число отсчетов, что облегчает выравнивание ${\displaystyle \,{\hat {u}}[n]\,}$ с ${\displaystyle \,u[n]\,,}$ создать аналитический сигнал. Групповая задержка типа IV находится на полпути между двумя сэмплами.

В MATLAB функция гильберт (u, N), сворачивает последовательность u [n] с периодическое суммирование:^[3]

${\displaystyle h_{N}[n]\ \triangleq \sum _{m=-\infty }^{\infty }h[n-mN]}$     ^[4]

и возвращает один цикл (N выборки) периодического результата в мнимой части комплексной выходной последовательности. Свертка реализуется в частотной области как произведение массива${\displaystyle \scriptstyle {\mathrm {DFT} }\displaystyle \left(u[n]\right)}$ с образцами −я sgn (ω) распределение (чьи действительные и мнимые компоненты равны 0 или±1). Рисунок 3 сравнивает полупериод час_N[п] с частью эквивалентной длины час[п]. Учитывая приближение FIR для ${\displaystyle \,h[n]\,,}$ обозначается ${\displaystyle \,{\tilde {h}}[n]\,,}$ замена ${\displaystyle \,\scriptstyle {\mathrm {DFT} }\displaystyle \left({\tilde {h}}[n]\right)\,}$ для −я sgn (ω) samples дает FIR-версию свертки.

Действительная часть выходной последовательности - это исходная входная последовательность, так что комплексный выход представляет собой аналитическое представление из ты[п]. Когда вход представляет собой сегмент чистого косинуса, результирующая свертка для двух разных значений N изображен в Рисунок 4 (красные и синие участки). Краевые эффекты не позволяют результату быть чистой синусоидальной функцией (зеленый график). С час_N[п] не является FIR-последовательностью, теоретическая степень воздействия - это вся выходная последовательность. Но отличия от синусоидальной функции уменьшаются по мере удаления от краев. Параметр N - длина выходной последовательности. Если он превышает длину входной последовательности, входные данные изменяются путем добавления элементов с нулевым значением. В большинстве случаев это уменьшает величину различий. Но их продолжительность определяется временем нарастания и спада час[п] импульсивный ответ.

Понимание краевых эффектов важно, когда метод, называемый перекрытие-сохранение используется для выполнения свертки на длинном ты[п] последовательность. Сегменты длины N свёртываются с периодической функцией:

${\displaystyle {\tilde {h}}_{N}[n]\ \triangleq \sum _{m=-\infty }^{\infty }{\tilde {h}}[n-mN].}$

Когда длительность ненулевых значений ${\displaystyle \,{\tilde {h}}[n]\,}$ является ${\displaystyle \,M<N\,,}$ выходная последовательность включает N − M + 1 образцы ${\displaystyle \,{\hat {u}}\,.}$ M − 1 выходы отбрасываются из каждого блока N, и входные блоки перекрываются на это количество, чтобы предотвратить пробелы.

Рисунок 5 является примером использования функции Гильберта (·) БИХ и приближения КИХ. В этом примере синусоидальная функция создается путем вычисления дискретного преобразования Гильберта косинусной функции, которая была обработана в четырех перекрывающихся сегментах и ​​снова собрана вместе. Как показывает результат КИХ (синий), искажения, заметные в результате КИХ (красный), не вызваны разницей между час[п] и час_N[п] (зеленый и красный в Рисунок 3). Дело в том, что час_N[п] конический (оконный) действительно полезен в этом контексте. Настоящая проблема в том, что у него недостаточно окон. Фактически, M = N , тогда как метод сохранения перекрытия требует M < N .

Теоретико-числовое преобразование Гильберта

Теоретико-числовое преобразование Гильберта является расширением (Как 1970 ) дискретного преобразования Гильберта к целым по модулю подходящего простого числа. Здесь следует обобщение дискретное преобразование Фурье к теоретико-числовым преобразованиям. Теоретико-числовое преобразование Гильберта можно использовать для генерации наборов ортогональных дискретных последовательностей (Как 2014 ).

Смотрите также

• Аналитический сигнал
• Гармонический конъюгат
• Гильбертова спектроскопия
• Преобразование Гильберта в комплексной плоскости
• Преобразование Гильберта – Хуанга
• Соотношение Крамерса – Кронига
• Преобразование Рисса
• Однополосный сигнал
• Сингулярные интегральные операторы типа свертки

Рекомендации

1. Видеть:
   • Баргманн 1947
   • Lang 1985
   • Сугиура 1990
2. Розенблюм и Ровняк 1997, п. 92
3. видеть Теорема свертки
4. Для четных значений N, эквивалентная закрытая форма:${\displaystyle h_{N}[n]={\begin{cases}{\frac {2}{N\tan(n\pi /N)}}&{\text{for }}n{\text{ odd}},\\0,&{\text{for }}n{\text{ even}},\end{cases}}}$
   Видеть http://www.rle.mit.edu/dspg/documents/HilbertComplete.pdf экв. (17), (18) и немеченое уравнение ниже (18).

Источники

• Баргманн, В. (1947). «Неприводимые унитарные представления группы Лоренца». Анна. математики. 48 (3): 568–640. Дои:10.2307/1969129. JSTOR  1969129.

• Бедросян, Э. (декабрь 1962 г.). Теорема произведения для преобразований Гильберта (PDF) (Отчет). Rand Corporation. RM-3439-PR.

• Бенедетто, Джон Дж. (1996). Гармонический анализ и его приложения. Бока-Ратон, Флорида: CRC Press. ISBN  0849378796.

• Бицадзе, А. (2001) [1994], «Краевые задачи теории аналитических функций», Энциклопедия математики, EMS Press

• Bracewell, R. (2000). Преобразование Фурье и его приложения (3-е изд.). Макгроу – Хилл. ISBN  0-07-116043-4.

• Кальдерон, А.; Зигмунд, А. (1952). «О существовании некоторых сингулярных интегралов». Acta Mathematica. 88 (1): 85–139. Дои:10.1007 / BF02392130.

• Карлсон; Крилли и Ратледж (2002). Системы связи (4-е изд.). ISBN  0-07-011127-8.

• Duoandikoetxea, J. (2000). Фурье-анализ. Американское математическое общество. ISBN  0-8218-2172-5.

• Duistermaat, J.J .; Колк, J.A.C. (2010). Распределения. Birkhäuser. Дои:10.1007/978-0-8176-4675-2. ISBN  978-0-8176-4672-1.

• Дурен, П. (1970). Теория ${\displaystyle H^{p}}$-Пространства. Нью-Йорк, Нью-Йорк: Academic Press.

• Фефферман, К. (1971). «Характеристики ограниченного среднего колебания». Бюллетень Американского математического общества. 77 (4): 587–588. Дои:10.1090 / S0002-9904-1971-12763-5. МИСТЕР  0280994.

• Fefferman, C .; Штейн, E.M. (1972). "ЧАС^п пространства нескольких переменных ». Acta Mathematica. 129: 137–193. Дои:10.1007 / BF02392215. МИСТЕР  0447953.

• Гельфанд, И.; Шилов, Г. (1968). Обобщенные функции. 2. Академическая пресса. С. 153–154. ISBN  0-12-279502-4.

• Графакос, Лукас (1994). «Элементарное доказательство суммируемости квадратов дискретного преобразования Гильберта». Американский математический ежемесячный журнал. Математическая ассоциация Америки. 101 (5): 456–458. Дои:10.2307/2974910. JSTOR  2974910.

• Графакос, Лукас (2004). Классический и современный анализ Фурье. Pearson Education. С. 253–257. ISBN  0-13-035399-X.

• Харди, Г.; Литтлвуд, Дж.; Поля, Г. (1952). Неравенства. Кембридж, Великобритания: Издательство Кембриджского университета. ISBN  0-521-35880-9.

• Гильберт, Дэвид (1953) [1912]. Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen [Основы общей теории линейных интегральных уравнений] (на немецком). Лейпциг и Берлин, Германия (1912 г.); Нью-Йорк, штат Нью-Йорк (1953): Б.Г. Тойбнер (1912); Chelsea Pub. Co. (1953). ISBN  978-3-322-00681-3. OCLC  988251080. Получено 2020-12-18 - через archive.org.

• Как, Субхаш (1970). «Дискретное преобразование Гильберта». Proc. IEEE. 58 (4): 585–586. Дои:10.1109 / PROC.1970.7696.

• Как, Субхаш (2014). "Теоретико-числовое преобразование Гильберта". Схемы Системы Обработки сигналов. 33 (8): 2539–2548. arXiv:1308.1688. Дои:10.1007 / s00034-014-9759-8. S2CID  21226699.

• Хведелидзе, Б.В. (2001) [1994], «Преобразование Гильберта», Энциклопедия математики, EMS Press

• Кинг, Фредерик В. (2009a). Преобразования Гильберта. 1. Кембридж, Великобритания: Издательство Кембриджского университета.

• Кинг, Фредерик В. (2009b). Преобразования Гильберта. 2. Кембридж, Великобритания: Издательство Кембриджского университета. п. 453. ISBN  978-0-521-51720-1.

• Кресс, Райнер (1989). Линейные интегральные уравнения. Нью-Йорк, штат Нью-Йорк: Springer-Verlag. п. 91. ISBN  3-540-50616-0.

• Ланг, Серж (1985). SL (2, ℝ). Тексты для выпускников по математике. 105. Нью-Йорк, штат Нью-Йорк: Springer-Verlag. ISBN  0-387-96198-4.

• Панди, Дж. (1996). Преобразование Гильберта распределений Шварца и приложения. Wiley-Interscience. ISBN  0-471-03373-1.

• Пихоридес, С. (1972). «О наилучшем значении констант в теоремах Рисса, Зигмунда и Колмогорова». Studia Mathematica. 44 (2): 165–179. Дои:10.4064 / см-44-2-165-179.

• Рис, Марсель (1928). "Sur les fonctions contuguées". Mathematische Zeitschrift. 27 (1): 218–244. Дои:10.1007 / BF01171098. S2CID  123261514.

• Розенблюм, Марвин; Ровняк, Джеймс (1997). Классы Харди и теория операторов. Дувр. ISBN  0-486-69536-0.

• Шварц, Лоран (1950). Теория распределений. Париж, Франция: Германн.

• Schreier, P .; Шарф, Л. (2010). Статистическая обработка комплексных данных: теория несобственных и некруглых сигналов. Кембридж, Великобритания: Издательство Кембриджского университета.

• Штейн, Элиас (1970). Сингулярные интегралы и свойства дифференцируемости функций. Издательство Принстонского университета. ISBN  0-691-08079-8.

• Штейн, Элиас; Вайс, Гвидо (1971). Введение в анализ Фурье на евклидовых пространствах. Издательство Принстонского университета. ISBN  0-691-08078-X.

• Сугиура, Мицуо (1990). Унитарные представления и гармонический анализ: введение. Математическая библиотека Северной Голландии. 44 (2-е изд.). Эльзевир. ISBN  0444885935.

• Титчмарш, Э. (1926). «Взаимные формулы с участием рядов и интегралов». Mathematische Zeitschrift. 25 (1): 321–347. Дои:10.1007 / BF01283842. S2CID  186237099.

• Титчмарш, Э. (1986) [1948]. Введение в теорию интегралов Фурье (2-е изд.). Оксфорд, Великобритания: Clarendon Press. ISBN  978-0-8284-0324-5.

• Зигмунд, Антони (1988) [1968]. Тригонометрический ряд (2-е изд.). Кембридж, Великобритания: Издательство Кембриджского университета. ISBN  978-0-521-35885-9.

внешняя ссылка

• Вывод ограниченности преобразования Гильберта.
• Mathworld преобразование Гильберта - Содержит таблицу преобразований
• Аналитические сигналы и фильтры преобразования Гильберта
• Вайсштейн, Эрик В. "Теорема Титчмарша". MathWorld.
• Йоханссон, Матиас. «Преобразование Гильберта» (PDF). Архивировано из оригинал (PDF) на 2012-02-05. резюме уровня студента преобразования Гильберта.
• "GS256 Лекция 3: Преобразование Гильберта" (PDF). Архивировано из оригинал (PDF) 27 февраля 2012 г. введение начального уровня в преобразование Гильберта.