Графеновая нанолента - Graphene nanoribbon

Графеновые наноленты (GNR, также называемый ленты из нанографена или же ленты из нанографита) являются полосками графен шириной менее 50 нм. Графеновые ленты были введены в качестве теоретической модели Мицутака Фудзита и соавторы исследовали краевой и наноразмерный размерный эффект в графене.[2][3][4]
Производство
Нанотомия
Большое количество ГНЛ с регулируемой шириной может быть произведено с помощью графитовой нанотомии,[5] где нанесение острого алмазного ножа на графит приводит к образованию наноблоков графита, которые затем можно расслаивать с образованием ГНЛ. GNR также можно изготавливать путем «расстегивания» или разрезания в осевом направлении. нанотрубки.[6] В одном из таких способов многослойные углеродные нанотрубки были распакованы в растворе действием перманганат калия и серная кислота.[7] В другом методе ГНЛ были получены плазменное травление нанотрубок, частично погруженных в полимер фильм.[8] Совсем недавно графеновые наноленты были выращены на Карбид кремния (SiC) подложки с использованием ионная имплантация с последующим вакуумным или лазерным отжигом.[9][10][11] Последний метод позволяет писать любой рисунок на подложках SiC с точностью до 5 нм.[12]
Эпитаксия
ЗНЛ выращивались на краях трехмерных структур, вытравленных в Карбид кремния вафли. Когда пластины нагреваются примерно до 1000 ° C (1270 K; 1830 ° F), кремний предпочтительно отталкивается по краям, образуя наноленты, структура которых определяется рисунком трехмерной поверхности. Ленты имели идеально гладкие края, отожженные в процессе изготовления. Измерения подвижности электронов, превышающие один миллион, соответствуют сопротивление листа 1 Ом на квадрат - на два порядка меньше, чем в двумерном графене.[13]
Химическое осаждение из паровой фазы
Наноленты шириной более 10 нм, выращенные на германий пластины действуют как полупроводники, демонстрируя запрещенная зона. Внутри реакционной камеры с помощью химическое осаждение из паровой фазы, метан используется для осаждения углеводородов на поверхности пластины, где они реагируют друг с другом, образуя длинные ленты с гладкими краями. Ленты были использованы для создания прототипа. транзисторы.[14] При очень низкой скорости роста кристаллы графена естественным образом превращаются в длинные наноленты на определенной германий хрустальная грань. Контролируя скорость роста и время роста, исследователи достигли контроля над шириной наноленты.[15]
Недавно исследователи из SIMIT (Шанхайский институт микросистем и информационных технологий Китайской академии наук) сообщили о стратегии выращивания графеновых нанолент с контролируемой шириной и гладкими краями непосредственно на диэлектрике. гексагональный нитрид бора (h-BN) субстраты.[16] Команда использует наночастицы никеля для травления канавок глубиной в один слой нанометров в h-BN, а затем заполняет их графеном, используя химическое осаждение из паровой фазы. Изменение параметров травления позволяет настраивать ширину канавки до менее 10 нм, и получаемые в результате ленты размером менее 10 нм демонстрируют ширину запрещенной зоны почти 0,5 эВ. Интегрируя эти наноленты в полевой транзистор устройств показывает соотношение включения и выключения более 104 при комнатной температуре, а также высокой подвижности носителей ~ 750 см2 V−1 s−1.
Многоступенчатый синтез наноленты
Был исследован восходящий подход.[17][18] В 2017 г. методом сухого контактного переноса аппликатор из стекловолокна, покрытый порошком графеновых нанолент атомарной точности, был прижат к пассивированной водородом поверхности Si (100) под вакуум. 80 из 115 GNR визуально закрывали решетку подложки со средней видимой высотой 0,30 нм. GNR не выравниваются по решетке Si, что указывает на слабую связь. Средняя ширина запрещенной зоны по 21 GNR составила 2,85 эВ со стандартным отклонением 0,13 эВ.[19]
Метод непреднамеренно перекрывает некоторые наноленты, что позволяет изучать многослойные ЗНЛ. Такие перекрытия могут быть созданы намеренно путем манипулирования сканирующий туннельный микроскоп. Депассивация водорода не оставила запрещенной зоны. Ковалентные связи между поверхностью Si и ГНЛ приводят к металлическому поведению. Поверхностные атомы Si движутся наружу, и ГНЛ изменяется от плоской до искаженной, при этом некоторые атомы C движутся к поверхности Si.[19]
Электронная структура
Электронные состояния ГНЛ во многом зависят от краевых структур (кресло или зигзаг). В зигзагообразных краях каждый последующий сегмент края находится под углом, противоположным предыдущему. В краях кресел каждая пара сегментов представляет собой поворот предыдущей пары на 120 / -120 градусов. Зигзагообразные края обеспечивают краевое локализованное состояние с несвязывающими молекулярными орбиталями вблизи энергии Ферми. Ожидается, что они будут иметь большие изменения в оптических и электронных свойствах от квантование.
Расчеты, основанные на теории сильной связи, предсказывают, что зигзагообразные ГНЛ всегда металлические, в то время как кресла могут быть металлическими или полупроводниковыми, в зависимости от их ширины. Тем не мение, теория функционала плотности Расчеты (DFT) показывают, что кресельные наноленты являются полупроводниками с масштабом запрещенной зоны, обратным ширине ГНР.[20] Эксперименты подтвердили, что энергетические щели увеличиваются с уменьшением ширины ГНЛ.[21] Графеновые наноленты с контролируемой ориентацией краев были изготовлены сканирующий туннельный микроскоп (СТМ) литография.[22] Сообщалось о разрыве энергии до 0,5 эВ в кресельной ленте шириной 2,5 нм.
Наноленты кресла бывают металлическими или полупроводниковыми и присутствуют спин поляризованный края. Их зазор открывается благодаря необычной антиферромагнитной связи между магнитные моменты на противоположных краях атомов углерода. Размер зазора обратно пропорционален ширине ленты.[23][24] и его поведение можно проследить до свойств пространственного распределения волновых функций краевых состояний и преимущественно локального характера обменного взаимодействия, порождающего спиновую поляризацию. Следовательно, квантовое ограничение, межрайний суперобмен и внутрикраевое прямое обменное взаимодействие в зигзагообразном ГНЛ важны для его магнетизма и запрещенной зоны. Краевой магнитный момент и ширина запрещенной зоны зигзагообразного ГНР обратно пропорциональны концентрации электронов / дырок, и ими можно управлять с помощью щелочного адатомы.[25]
Их двухмерная структура, высокая электрическая и теплопроводность и низкий уровень шума также делают GNR возможной альтернативой меди для межсоединений интегральных схем. Исследования изучают создание квантовых точек путем изменения ширины GNR в выбранных точках вдоль ленты, создавая квантовое ограничение.[26] Были реализованы гетеропереходы внутри отдельных графеновых нанолент, среди которых было показано, что структуры функционируют как туннельные барьеры.
Наноленты графена обладают полупроводниковый свойств и может быть технологической альтернативой кремниевые полупроводники[27] способный выдержать микропроцессор тактовые частоты в районе 1 ТГц[28] полевые транзисторы шириной менее 10 нм были созданы с помощью GNR - "GNRFETs" - с буквой I.на/Явыключенный соотношение> 106 при комнатной температуре.[29][30]
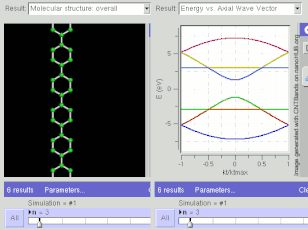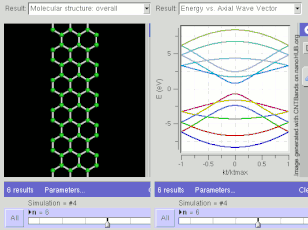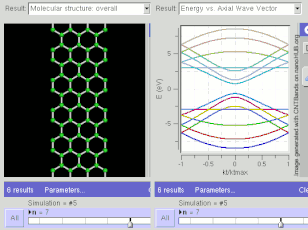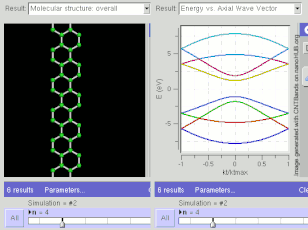
Структура ленты GNR для кресельного типа. Расчеты жесткой привязки показывают, что кресло может быть полупроводниковым или металлическим, в зависимости от ширины (хиральности).

Структура полосы ГНР для типа зигзаг. Расчеты жесткой привязки предсказывают, что зигзагообразный тип всегда металлический.

ТЕМ микрофотографии ЗНЛ (a) w = 15, (b) w = 30, (c) w = 40 (расслаивание) и (d) w = 60 нм, нанесенных на сетку из кружевного углерода 400 меш и (e) микрофотография FESEM Лента 600 нм. (f) Электронно-микроскопические изображения 120-нм графеновых лент (FESEM), (g) квадратные GQD 50 нм (FESEM), (h, i) прямоугольные GQD 25 × 100 нм2 (FESEM) и (j) 8 ° - угловой конический GNR (или треугольный GQD) (FESEM)). Большие плотности квадратных и прямоугольных GQD (g) показали обширную складчатость (белые стрелки). Размеры стержней = (а) 250 нм, (б, ж, и) 50 нм, (в, г) 500 нм и (з) 1 мкм.[5]
Механические свойства
Хотя трудно приготовить графеновые наноленты с точной геометрией для проведения реальных Тест на растяжку из-за предельного разрешения в нанометровом масштабе механические свойства двух наиболее распространенных графеновых нанолент (зигзагообразной и кресельной) были исследованы с помощью компьютерного моделирования с использованием теория функционала плотности, молекулярная динамика, и метод конечных элементов. Поскольку двумерный графен лист с прочным склеиванием, как известно, является одним из самых жестких материалов, графеновых нанолент Модуль для младших также имеет значение более 1 ТПа.[31][32][33]
Модуль Юнга, модуль сдвига и Коэффициент Пуассона Графеновые наноленты различаются размерами (длиной и шириной) и формами. Эти механические свойства являются анизотропными и обычно обсуждаются в двух направлениях в плоскости, параллельном и перпендикулярном одномерному периодическому направлению. Механические свойства здесь будут немного отличаться от двухмерных графеновых листов из-за отличной геометрии, длины связи и прочности связи, особенно на краях графеновых нанолент.[31] Эти наномеханические свойства можно регулировать с помощью дальнейшего химического легирования, чтобы изменить среду связывания на краю графеновых нанолент.[32] При увеличении ширины графеновых нанолент механические свойства будут приближаться к значению, измеренному на листах графена.[31][32] В одном из анализов методом молекулярной динамики был предсказан высокий модуль Юнга для кресельных графеновых нанолент, составляющий около 1,24 ТПа.[31] Они также показали нелинейное упругое поведение с членами более высокого порядка в напряжение-деформация изгиб. В области более высоких деформаций потребуется еще более высокий порядок (> 3) для полного описания нелинейного поведения. Другие ученые также сообщили о нелинейной упругости методом конечных элементов и обнаружили, что модуль Юнга, предел прочности, и пластичность Графеновых нанолент кресел все больше, чем у зигзагообразных графеновых нанолент.[34] Другой отчет предсказал линейную упругость для деформации от -0,02 до 0,02 на зигзагообразных графеновых нанолентах с помощью модели теории функционала плотности.[32] В линейной области электронные свойства будут относительно стабильными при незначительном изменении геометрии. Энергетические щели увеличиваются с -0,02 эВ до 0,02 эВ для деформации от -0,02 до 0,02, что обеспечивает возможности для будущих инженерных приложений.
В предел прочности кресельной графеновой наноленты составляет 175 ГПа с большой пластичностью 30,26% перелом напряжение,[31] который показывает более высокие механические свойства по сравнению с величиной 130 ГПа и 25%, экспериментально измеренной на однослойном графене.[35] Как и ожидалось, графеновые наноленты с меньшей шириной будут полностью разрушаться быстрее, так как доля более слабых краевых связей увеличивается. В то время как растягивающая деформация графеновых нанолент достигла своего максимума, связи C-C начнут разрываться, а затем образуются кольца гораздо большего размера, что сделает материалы более слабыми до разрушения.[31]
Оптические свойства
Первые численные результаты по оптическим свойствам графеновых нанолент были получены Лином и Шю в 2000 году.[36] Разные правила отбора для оптических переходов в графеновых нанолентах с креслом и зигзагообразными краями. Эти результаты были дополнены сравнительным исследованием зигзагообразных нанолент с одностенным креслом. углеродные нанотрубки Сюй и Райхль в 2007.[37] Было продемонстрировано, что правила отбора в зигзагообразных лентах отличаются от правил отбора в углеродных нанотрубках, а собственные состояния в зигзагообразных лентах можно классифицировать как симметричные или антисимметричные. Также было предсказано, что краевые состояния должны играть важную роль в оптическом поглощении зигзагообразных нанолент. Оптические переходы между краевым и объемным состояниями должны обогатить область низких энергий ( эВ) спектра поглощения сильными пиками поглощения. Аналитический вывод численно полученных правил отбора был представлен в 2011 году.[38][39] Правило отбора для падающего света, поляризованного продольно оси зигзагообразной ленты, таково: нечетно, где и пронумеровать энергетические зоны, а для перпендикулярной поляризации даже. Внутризонные (межподзонные) переходы между проводимостью (валентностью) поддиапазоны также разрешены, если даже.

Для графеновых нанолент с кресельными краями правило выбора: . Подобно переходам в трубках, межподзонные переходы запрещены для кресельных графеновых нанолент. Несмотря на разные правила отбора в одностенных кресельных углеродных нанотрубках и зигзагообразных графеновых нанолентах, предсказывается скрытая корреляция пиков поглощения.[40] Корреляция пиков поглощения в трубках и лентах должна иметь место, когда число атомов в элементарной ячейке трубки связано с числом атомов в элементарной ячейке зигзагообразной ленты следующее: , которое является так называемым условием согласования периодических и жестких граничных условий. Вышеупомянутые результаты были получены в приближении ближайших соседей модели сильной связи без учета экситонных эффектов.
Расчеты из первых принципов с квазичастичными поправками и многочастичными эффектами исследовали электронные и оптические свойства материалов на основе графена.[41] С помощью расчета GW точно исследуются свойства материалов на основе графена, включая графеновые наноленты,[42] Графеновые наноленты с функционализированными краями и поверхностью кресла[43] и масштабирующие свойства в кресельных графеновых нанолентах.[44]
Анализирует
Наноленты графена можно анализировать с помощью сканирующего туннельного микроскопа, рамановской спектроскопии,[45][46] ИК-спектроскопия,[47][48] и рентгеновская фотоэлектронная спектроскопия.[49] Например, изгибающая вибрация вне плоскости одного C-H на одном бензольном кольце, называемая SOLO, которая похожа на зигзагообразный край, на зигзагообразных GNR, как сообщается, появляется на расстоянии 899 см.−1, в то время как два C-H на одном бензольном кольце, называемом DUO, который похож на край кресла, на кресельных GNR, как сообщается, появляется на расстоянии 814 см.−1 как результат расчетных ИК-спектров.[48] Однако анализ графеновой наноленты на подложках затруднен с использованием инфракрасной спектроскопии даже с использованием метода спектрометрии отраженного поглощения. Таким образом, для анализа инфракрасной спектроскопии необходимо большое количество графеновой наноленты.
Реактивность
Зигзагообразные края, как известно, более реактивны, чем края кресел, что наблюдается по реактивности дегидрирования между компаундом с зигзагообразными краями (тетрацен) и краями кресла (хризен).[50] Кроме того, зигзагообразные края обычно более окисляются, чем края кресел без газификации.[51] Зигзагообразные края с большей длиной могут быть более реактивными, как это видно из зависимости длины аценов от реакционной способности.[52]
Приложения
Полимерные нанокомпозиты
Наноленты графена и их окисленные аналоги, называемые нанолентами оксида графена, были исследованы в качестве нанонаполнителей для улучшения механических свойств полимерных нанокомпозитов. Наблюдалось повышение механических свойств эпоксидных композитов при нагружении графеновых нанолент.[53] Повышение механических свойств биоразлагаемых полимерных нанокомпозитов из полипропиленфумарата при низком весовом процентном содержании было достигнуто за счет загрузки оксидированных графеновых нанолент, изготовленных для инженерии костной ткани.[54]
Контрастный агент для биовизуализации
Гибридные методы визуализации, такие как фотоакустическая (PA) томография (PAT) и термоакустическая (ТА) томография (ТАТ) были разработаны для биовизуализация Приложения. PAT / TAT сочетает в себе преимущества чистого УЗИ и чисто оптическая визуализация /радиочастота (RF), обеспечивая хорошее пространственное разрешение, большую глубину проникновения и высокий контраст мягких тканей. ГНР синтезируется распаковкой одностенных и многостенных углеродные нанотрубки были зарегистрированы как контрастные вещества для фотоакустической и термоакустической визуализации и томография.[55]
Смотрите также
- Графен
- Графитовый
- Бумага из оксида графена
- Углеродная нанотрубка
- Мицутака Фудзита
- Кацунори Вакабаяси
- Силицен, которые также могут образовывать наноленты
- Графеновая электроника
Рекомендации
- ^ Кавай, Шигеки; Сайто, Шохей; Осуми, Шиничиро; Ямагути, Сигехиро; Фостер, Адам С .; Спайкер, Питер; Мейер, Эрнст (2015). «Атомно-контролируемое замещающее легирование бором графеновых нанолент». Nature Communications. 6: 8098. Bibcode:2015НатКо ... 6.8098K. Дои:10.1038 / ncomms9098. ЧВК 4560828. PMID 26302943.
- ^ Fujita M .; Wakabayashi K .; Nakada K .; Кусакабэ К. (1996). «Своеобразное локализованное состояние на краю зигзагообразного графита». Журнал Физического общества Японии. 65 (7): 1920. Bibcode:1996JPSJ ... 65.1920F. Дои:10.1143 / JPSJ.65.1920.
- ^ Nakada K .; Fujita M .; Dresselhaus G .; Дрессельхаус М.С. (1996). «Краевое состояние в графеновых лентах: размерный эффект нанометра и зависимость формы края». Физический обзор B. 54 (24): 17954–17961. Bibcode:1996ПхРвБ..5417954Н. Дои:10.1103 / PhysRevB.54.17954. PMID 9985930.
- ^ Wakabayashi K .; Fujita M .; Ajiki H .; Сигрист М. (1999). «Электронные и магнитные свойства нанографитовых лент». Физический обзор B. 59 (12): 8271–8282. arXiv:cond-mat / 9809260. Bibcode:1999PhRvB..59.8271W. Дои:10.1103 / PhysRevB.59.8271. S2CID 119523846.
- ^ а б Моханти, Нихар; Мур, Дэвид; Сюй, Чжипин; Sreeprasad, T.S .; Нагараджа, Ашвин; Родригес, Альфредо Александр; Берри, Викас (2012). «Производство переносимых и диспергируемых графеновых наноструктур контролируемой формы и размера на основе нанотомии» (PDF). Nature Communications. 3 (5): 844. Bibcode:2012 НатКо ... 3E.844M. Дои:10.1038 / ncomms1834. PMID 22588306.
- ^ Брамфил, Г. (2009). «Нанотрубки, разрезанные на ленты. Новые технологии открывают углеродные трубки для создания лент». Природа. Дои:10.1038 / новости.2009.367.
- ^ Косынкин, Дмитрий В .; Хиггинботам, Аманда Л .; Синицкий, Александр; Ломеда, Джей Р .; Димиев, Айрат; Прайс, Б. Кэтрин; Тур, Джеймс М. (2009). «Продольное расстегивание углеродных нанотрубок с образованием графеновых нанолент». Природа. 458 (7240): 872–6. Bibcode:2009Натура.458..872K. Дои:10.1038 / природа07872. HDL:10044/1/4321. PMID 19370030. S2CID 2920478.
- ^ Лиин Цзяо; Ли Чжан; Синьран Ван; Георгий Дианков; Хунцзе Дай (2009). «Узкие графеновые наноленты из углеродных нанотрубок». Природа. 458 (7240): 877–80. Bibcode:2009Натура.458..877J. Дои:10.1038 / природа07919. PMID 19370031. S2CID 205216466.
- ^ "Написание графеновых схем ионными перьями'". ScienceDaily. 27 марта 2012 г.. Получено 29 августа 2012.
- ^ "Основные новости физики AIP 27 марта 2012 г.". Американский институт физики (AIP). 2012-03-28. Получено 29 августа 2012.
- ^ Тонгай, S .; Lemaitre, M .; Fridmann, J .; Hebard, A. F .; Gila, B.P .; Эпплтон, Б. Р. (2012). «Нанесение графеновых нанолент на SiC методом ионной имплантации». Appl. Phys. Латыш. 100 (73501): 073501. Bibcode:2012АпФЛ.100г3501Т. Дои:10.1063/1.3682479.
- ^ "Написание графеновых схем ионными перьями'". Американский институт физики. Новости Nanowerk. 27 марта 2012 г.. Получено 29 августа 2012.
- ^ «Новая форма графена позволяет электронам вести себя как фотоны». kurzweilai.net. 6 февраля 2014 г.. Получено 11 октября, 2015.
- ^ Оркатт, Майк (13 августа 2015 г.). «Новая техника дает графеновым транзисторам необходимое преимущество | Обзор технологий MIT». Обзор технологий MIT. Получено 2015-10-11.
- ^ "'Конструкция кресла с нанолентой делает графен масштабируемым полупроводником | KurzweilAI ". www.kurzweilai.net. 19 августа 2015 г.. Получено 2015-10-13.
- ^ Чен, Линсю; Он, Ли; Ван, Хуэйшань (2017). «Ориентированные графеновые наноленты, внедренные в канавки гексагонального нитрида бора». Nature Communications. 8: 14703. arXiv:1703.03145. Bibcode:2017НатКо ... 814703C. Дои:10.1038 / ncomms14703. ЧВК 5347129. PMID 28276532.
- ^ Ян, X .; Доу, X .; Rouhanipour, A .; Zhi, L .; Räder, H.J .; Мюллен, К. (2008). «Двумерные графеновые наноленты». Журнал Американского химического общества. 130 (13): 4216–4217. Дои:10.1021 / ja710234t. PMID 18324813.
- ^ Dössel, L .; Gherghel, L .; Feng, X .; Мюллен, К. (2011). «Графеновые наноленты от химиков: нанометровые, растворимые и бездефектные». Angewandte Chemie International Edition. 50 (11): 2540–3. Дои:10.1002 / anie.201006593. PMID 21370333.
- ^ а б «Институт Форсайта» Блог »Чистое размещение графеновых нанолент атомарной точности». www.foresight.org. Получено 2017-02-15.
- ^ Barone, V .; Hod, O .; Скузерия, Г. Э. (2006). «Электронная структура и стабильность полупроводниковых графеновых нанолент». Нано буквы. 6 (12): 2748–54. Bibcode:2006NanoL ... 6.2748B. Дои:10.1021 / nl0617033. PMID 17163699.
- ^ Han., M.Y .; Özyilmaz, B .; Zhang, Y .; Ким, П. (2007). "Энергетическая ширина запрещенной зоны графеновых нанолент". Письма с физическими проверками. 98 (20): 206805. arXiv:cond-mat / 0702511. Bibcode:2007ПхРвЛ..98т6805Н. Дои:10.1103 / PhysRevLett.98.206805. PMID 17677729. S2CID 6309177.
- ^ Tapasztó, Левенте; Добрик, Гергей; Ламбен, Филипп; Биро, Ласло П. (2008). «Настройка атомной структуры графеновых нанолент с помощью литографии на сканирующем туннельном микроскопе». Природа Нанотехнологии. 3 (7): 397–401. arXiv:0806.1662. Дои:10.1038 / nnano.2008.149. PMID 18654562. S2CID 20231725.
- ^ Сын Ю.-З .; Cohen M. L .; Луи С. Г. (2006). «Энергетические щели в графеновых нанолентах». Письма с физическими проверками. 97 (21): 216803. arXiv:cond-mat / 0611602. Bibcode:2006ПхРвЛ..97у6803С. Дои:10.1103 / PhysRevLett.97.216803. PMID 17155765. S2CID 536865.
- ^ Юнг. J .; Pereg-Barnea T .; Макдональд А. Х. (2009). "Теория сверхобмена в зигзагообразном магнетизме". Письма с физическими проверками. 102 (22): 227205. arXiv:0812.1047. Bibcode:2009PhRvL.102v7205J. Дои:10.1103 / PhysRevLett.102.227205. PMID 19658901. S2CID 6539197.
- ^ Хуанг, Лян Фэн; Чжан, Го Жэнь; Чжэн, Сяо Хун; Гонг, Пэн Лай; Цао, Дэн Фэй; Цзэн, Чжи (2013). «Понимание и настройка эффекта ограничения квантов и краевого магнетизма в зигзагообразной графеновой наноленте». J. Phys .: Condens. Иметь значение. 25 (5): 055304. Bibcode:2013JPCM ... 25e5304H. Дои:10.1088/0953-8984/25/5/055304. PMID 23300171.
- ^ Wang, Z. F .; Shi, Q.W .; Li, Q .; Ван, X .; Hou, J. G .; Zheng, H .; Yao, Y .; Чен, Дж. (2007). «Z-образное устройство с квантовыми точками из графеновой наноленты». Письма по прикладной физике. 91 (5): 053109. arXiv:0705.0023. Bibcode:2007ApPhL..91e3109W. Дои:10.1063/1.2761266.
- ^ Буллис, Кевин (28 января 2008 г.). «Графеновые транзисторы». Обзор технологий. Кембридж: Массачусетский технологический институт Technology Review, Inc. Получено 2008-02-18.
- ^ Буллис, Кевин (25 февраля 2008 г.). «TR10: графеновые транзисторы». Обзор технологий. Кембридж: Массачусетский технологический институт Technology Review, Inc. Получено 2008-02-27.
- ^ Ван, Синьрань; Оуян, Ицзянь; Ли, Сяолинь; Ван, Хайлянь; Го, Цзин; Дай, Хунцзе (2008). "Полупроводниковые полупроводниковые полевые транзисторы с нанолентой и графеном толщиной менее 10 нм при комнатной температуре". Письма с физическими проверками. 100 (20): 206803. arXiv:0803.3464. Bibcode:2008PhRvL.100t6803W. Дои:10.1103 / PhysRevLett.100.206803. PMID 18518566. S2CID 12833620.
- ^ Баллон, М. С. (28 мая 2008 г.). Углеродные наноленты позволяют создавать более компактные и быстрые компьютерные чипы. Стэнфордский отчет
- ^ а б c d е ж Бу, Хао; Чен, Юньфэй; Цзоу, Мин; Йи, Хун; Би, Кедонг; Ни, Чжунхуа (22 июля 2009 г.). «Атомистическое моделирование механических свойств графеновых нанолент». Письма о физике A. 373 (37): 3359–3362. Дои:10.1016 / j.physleta.2009.07.048.
- ^ а б c d Фаччо, Рикардо; Денис, Пабло; Пардо, Елена; Гойенола, Сесилия; Момбру, Альваро (19 июня 2009 г.). «Механические свойства графеновых нанолент». Журнал физики: конденсированное вещество. 21 (28): 285304. arXiv:0905.1440. Дои:10.1088/0953-8984/21/28/285304. PMID 21828517. S2CID 5099613 - через IOPscience.
- ^ Георганцинос, С.К .; Giannopoulos, G.I .; Анифантис, Н. (Декабрь 2010 г.). «Численное исследование упругих механических свойств графеновых структур». Материалы и дизайн. 31 (10): 4646–4654. Дои:10.1016 / j.matdes.2010.05.036.
- ^ Георганцинос, С.К .; Giannopoulos, G.I .; Katsareas, D.E .; Kakavas, P.A .; Анифантис, Н. (Май 2011 г.). «Нелинейные механические свойства графеновых нанолент в зависимости от размера». Вычислительное материаловедение. 50 (7): 2057–2062. Дои:10.1016 / j.commatsci.2011.02.008.
- ^ Чангу, Ли; Вэй, Сяодин; Кайсар, Джеффри; Хон, Джеймс (18 июля 2008 г.). «Измерение упругих свойств и внутренней прочности однослойного графена». Наука. 321 (5887): 385–388. Bibcode:2008Sci ... 321..385L. Дои:10.1126 / science.1157996. PMID 18635798. S2CID 206512830.
- ^ Линь, Мин-Фа; Шю, Фэн-Линь (2000). «Оптические свойства нанографитовых лент». J. Phys. Soc. JPN. 69 (11): 3529. Bibcode:2000JPSJ ... 69.3529L. Дои:10.1143 / JPSJ.69.3529.
- ^ Сюй, Хан; Райхль, Л. (2007). «Правило выбора оптического поглощения графеновых нанолент». Phys. Ред. B. 76 (4): 045418. Bibcode:2007PhRvB..76d5418H. Дои:10.1103 / PhysRevB.76.045418.
- ^ Chung, H.C .; Lee, M. H .; Chang, C.P .; Линь М.Ф. (2011). «Исследование краевых оптических правил отбора для графеновых нанолент». Оптика Экспресс. 19 (23): 23350–63. arXiv:1104.2688. Bibcode:2011OExpr..1923350C. Дои:10.1364 / OE.19.023350. PMID 22109212.
- ^ Сасаки, К.-И .; Като, К .; Tokura, Y .; Огури, К .; Согава, Т. (2011). «Теория оптических переходов в графеновых нанолентах». Phys. Ред. B. 84 (8): 085458. arXiv:1107.0795. Дои:10.1103 / PhysRevB.84.085458. S2CID 119091338.
- ^ Сарока, В. А .; Шуба, М. В .; Портной, М. Э. (2017). «Правила оптического отбора зигзагообразных графеновых нанолент». Phys. Ред. B. 95 (15): 155438. arXiv:1705.00757. Bibcode:2017PhRvB..95o5438S. Дои:10.1103 / PhysRevB.95.155438.
- ^ Онида, Джованни; Рубио, Ангел (2002). «Электронные возбуждения: подходы с функцией плотности и функции Грина для многих тел». Ред. Мод. Phys. 74 (2): 601. Bibcode:2002RvMP ... 74..601O. Дои:10.1103 / RevModPhys.74.601. HDL:10261/98472.
- ^ Преззи, Дебора; Варсано, Даниэле; Руини, Алиса; Марини, Андреа; Молинари, Элиза (2008). «Оптические свойства графеновых нанолент: роль многочастичных эффектов». Физический обзор B. 77 (4): 041404. arXiv:0706.0916. Bibcode:2008PhRvB..77d1404P. Дои:10.1103 / PhysRevB.77.041404. S2CID 73518107.
Ян, Ли; Коэн, Марвин Л .; Луи, Стивен Г. (2007). «Экситонные эффекты в оптических спектрах графеновых нанолент». Nano Lett. 7 (10): 3112–5. arXiv:0707.2983. Bibcode:2007NanoL ... 7.3112Y. Дои:10.1021 / nl0716404. PMID 17824720. S2CID 16943236.
Ян, Ли; Коэн, Марвин Л .; Луи, Стивен Г. (2008). "Магнитные экситоны краевого состояния в зигзагообразных графеновых нанолентах". Письма с физическими проверками. 101 (18): 186401. Bibcode:2008PhRvL.101r6401Y. Дои:10.1103 / PhysRevLett.101.186401. PMID 18999843. - ^ Чжу, Си; Су, Хайбин (2010). «Экситоны краевых и поверхностных функционализированных графеновых нанолент». J. Phys. Chem. C. 114 (41): 17257. Дои:10.1021 / jp102341b.
- ^ Чжу, Си; Су, Хайбин (2011). "Масштабирование экситонов в графеновых нанолентах с краями в форме кресла". Журнал физической химии А. 115 (43): 11998–12003. Bibcode:2011JPCA..11511998Z. Дои:10.1021 / jp202787h. PMID 21939213.
- ^ Цай, Цзиньминь; Паскаль Руффье; Рачед Джаафар; Марко Бьери; и другие. (22 июля 2010 г.). «Производство графеновых нанолент с атомарной точностью снизу вверх». Природа. 466 (7305): 470–473. Bibcode:2010Натура.466..470C. Дои:10.1038 / природа09211. PMID 20651687. S2CID 4422290.
- ^ Ким, Юнгпил; Ли, Нодо; Мин, Ён Хван; Но, Сохван; Ким, Нам-Ку; Юнг, Соквон; Джу, Минхо; Ямада, Ясухиро (2018-12-31). «Определение зигзагообразных и кресельных краев графеновых нанолент с помощью рентгеновской фотоэлектронной и рамановской спектроскопии». СКУД Омега. 3 (12): 17789–17796. Дои:10.1021 / acsomega.8b02744. ISSN 2470-1343. ЧВК 6643467. PMID 31458375.
- ^ Сасаки, Тацуя; Ясухиро Ямада; Сатоши Сато (6 августа 2018 г.). «Количественный анализ кромок зигзага и кресел на углеродных материалах с пятиугольниками и без них с помощью инфракрасной спектроскопии». Аналитическая химия. 90 (18): 10724–10731. Дои:10.1021 / acs.analchem.8b00949. PMID 30079720.
- ^ а б Ямада, Ясухиро; Масаки, Сиори; Сато, Сатоши (01.08.2020). «Бромированные позиции на графеновой наноленте проанализированы с помощью инфракрасной спектроскопии». Журнал материаловедения. 55 (24): 10522–10542. Дои:10.1007 / s10853-020-04786-1. ISSN 1573-4803. S2CID 218624238.
- ^ Ким, Юнгпил; Ли, Нодо; Мин, Ён Хван; Но, Сохван; Ким, Нам-Ку; Юнг, Соквон; Джу, Минхо; Ямада, Ясухиро (2018-12-31). «Определение зигзагообразных и кресельных краев на графеновых нанолентах с помощью рентгеновской фотоэлектронной и рамановской спектроскопии». СКУД Омега. 3 (12): 17789–17796. Дои:10.1021 / acsomega.8b02744. ISSN 2470-1343. ЧВК 6643467. PMID 31458375.
- ^ Ямада, Ясухиро; Каваи, Мики; Ёримицу, Хидеки; Оцука, Шинья; Таканаши, Мотохару; Сато, Сатоши (28.11.2018). «Углеродные материалы с зигзагообразными и кресельными краями». Прикладные материалы и интерфейсы ACS. 10 (47): 40710–40739. Дои:10.1021 / acsami.8b11022. ISSN 1944-8244.
- ^ Ямада, Ясухиро; Каваи, Мики; Ёримицу, Хидеки; Оцука, Шинья; Таканаши, Мотохару; Сато, Сатоши (28.11.2018). «Углеродные материалы с зигзагообразными и кресельными краями». Прикладные материалы и интерфейсы ACS. 10 (47): 40710–40739. Дои:10.1021 / acsami.8b11022. ISSN 1944-8244.
- ^ Zade, Sanjio S .; Бендиков, Михаил (2012). «Реакционная способность аценов: механизмы и зависимость от длины аценов». Журнал физической органической химии. 25 (6): 452–461. Дои:10.1002 / poc.1941. ISSN 1099-1395.
- ^ Райфи, Мохаммад; Вэй Лу; Абхай В. Томас; Ардаван Зандиаташбар; Джавад Рафи; Джеймс М. Тур (16 ноября 2010 г.). «Композиты из графеновых нанолент». САУ Нано. 4 (12): 7415–7420. Дои:10.1021 / nn102529n. PMID 21080652.
- ^ Лалвани, Гаурав; Аллан М. Хенсли; Бехзад Фаршид; Лянцзюнь Линь; Ф. Куртис Каспер; И-Сянь Цинь; Антониос Г. Микос; Баладжи Ситхараман (2013). "Двумерные биоразлагаемые полимерные нанокомпозиты, усиленные наноструктурами, для инженерии костной ткани". Биомакромолекулы. 14 (3): 900–9. Дои:10.1021 / BM301995s. ЧВК 3601907. PMID 23405887.
- ^ Лалвани, Гаурав; Синь Цай; Извещение Не; Лихонг В. Ван; Баладжи Ситхараман (декабрь 2013 г.). «Контрастные вещества на основе графена для фотоакустической и термоакустической томографии». Фотоакустика. 1 (3–4): 62–67. Дои:10.1016 / j.pacs.2013.10.001. ЧВК 3904379. PMID 24490141.Полный текст PDF.











