Окончательная звездчатость икосаэдра - Final stellation of the icosahedron

Окончательная звездчатость икосаэдра
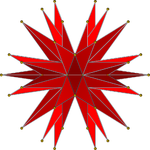Два симметричных орфографические проекции
Группа симметрии	икосаэдр (ячас)
Тип	Звездчатый икосаэдр, 8 из 59
Символы	Du Val ЧАС Веннингер: W42
Элементы (Как звездный многогранник)	F = 20, E = 90 V = 60 (χ = −10)
Элементы (Как простой многогранник)	F = 180, E = 270, V = 92 (χ = 2)
Характеристики (Как звездный многогранник)	Вершинно-транзитивный, лицо переходный
Звездчатая диаграмма Звездчатость основной Выпуклый корпус Икосаэдр усеченный икосаэдр

В геометрия, то полный или же окончательная звездчатость икосаэдра^[1][2] самый внешний звездчатость из икосаэдр, и является "полным" и "окончательным", потому что включает все ячейки в икосаэдре звездчатая диаграмма. То есть каждые три пересекающиеся плоскости граней ядра икосаэдра пересекаются либо в вершине этого многогранника, либо внутри него.

Этот многогранник семнадцатый звездчатость из икосаэдр, и задано как Индекс модели Веннингера 42.

Как геометрическая фигура, она имеет две интерпретации, описанные ниже:

• Как нерегулярный звездный (самопересекающийся) многогранник с 20 идентичными самопересекающимися эннеаграмматический граней, 90 ребер, 60 вершин.
• Как простой многогранник с 180 треугольными гранями (60 равнобедренных, 120 разносторонних), 270 ребер и 92 вершины. Эта интерпретация полезна для модель многогранника строительство.

Иоганн Кеплер исследовали звездчатые образования, образующие правильные звездные многогранники ( Многогранники Кеплера-Пуансо ) в 1619 г., но полный икосаэдр с неправильными гранями был впервые изучен в 1900 г. Макс Брюкнер.

История

Модель Брюкнера (Таф. XI, рис. 14, 1900 г.)[3]

Ехидна

• 1619: В Harmonices Mundi, Иоганн Кеплер впервые применил звездчатый процесс, признав малый звездчатый додекаэдр и большой звездчатый додекаэдр как правильные многогранники.^[4]
• 1809: Луи Пуансо заново открыл многогранники Кеплера и еще два, большой икосаэдр и большой додекаэдр как правильные звездные многогранники, теперь называемые Многогранники Кеплера – Пуансо.^[5]
• 1812: Огюстен-Луи Коши сделал дальнейшее перечисление звездных многогранников, доказав, что существует только 4 правильных звездных многогранника.^[6]
• 1900: Макс Брюкнер расширил теорию звездчатости за пределы регулярных форм и идентифицировал десять звездчатых образов икосаэдра, включая полная звездчатость.^[3]
• 1924: А.Х. Уиллер в 1924 году опубликовал список из 20 звездчатых форм (22 включая светоотражающие копии), в том числе полная звездчатость.^[7]
• 1938: В их книге 1938 года Пятьдесят девять икосаэдров, Х. С. М. Коксетер, П. Дю Валь, Г. Т. Флатер и Дж. Ф. Петри сформулировали набор правил звездчатости для правильного икосаэдра и дали систематический перечень пятидесяти девяти звездчатых форм, которые соответствуют этим правилам. Полная звездчатая форма упоминается как восьмая в книге.
• 1974: В Веннингер книга 1974 года Модели многогранников, последняя звездчатая форма икосаэдра включена как 17-я модель звездчатых икосаэдров с порядковым номером W₄₂.
• 1995: Эндрю Хьюм назвал это в своей Netlib многогранная база данных как ехиднаэдр^[8] (в ехидна, или колючий муравьед - маленький млекопитающее что покрыто грубым волосы и шипы и которая сворачивается в клубок, чтобы защитить себя).

Интерпретации

Звездчатая диаграмма икосаэдра с пронумерованными ячейками. Полный икосаэдр состоит из всех ячеек звездчатой ​​формы, но видны только самые внешние области, обозначенные на схеме цифрой «13».

3D-модель финальной звездчатой ​​формы икосаэдра

Как звездочка

Основная статья: Пятьдесят девять икосаэдров

В звездчатость многогранника расширяет грани многогранника на бесконечные плоскости и порождает новый многогранник, который ограничен этими плоскостями как гранями и пересечениями этих плоскостей как ребрами. Пятьдесят девять икосаэдров перечисляет звёздчатые формы регулярных икосаэдр, в соответствии с набором правил, выдвинутых Дж. С. П. Миллер, в том числе полная звездчатость. Символ Дю Валя полной звездчатой ​​формы - ЧАС, поскольку он включает все ячейки на звездчатой ​​диаграмме до самого внешнего слоя «h» включительно.^[6]

Как простой многогранник

А многогранная модель может быть построен из 12 наборов граней, каждая из которых сложена в группу из пяти пирамид.

В виде простого многогранника с видимой поверхностью внешняя форма конечной звездообразной формы состоит из 180 треугольных граней, которые являются крайними треугольными областями на звездчатой ​​диаграмме. Они соединяются по 270 ребрам, которые, в свою очередь, пересекаются в 92 вершинах с Эйлерова характеристика из 2.^[9]

92 вершины лежат на поверхностях трех концентрических сфер. Самая внутренняя группа из 20 вершин образует вершины правильного додекаэдра; следующий слой из 12 образуют вершины правильного икосаэдра; а внешний слой из 60 образуют вершины неоднородного усеченного икосаэдра. Радиусы этих сфер находятся в соотношении^[10]

${\displaystyle {\sqrt {{\frac {3}{2}}\left(3+{\sqrt {5}}\right)}}\,:\,{\sqrt {{\frac {1}{2}}\left(25+11{\sqrt {5}}\right)}}\,:\,{\sqrt {{\frac {1}{2}}\left(97+43{\sqrt {5}}\right)}}\,.}$

Выпуклые оболочки каждой сферы вершин

Внутренний	Середина	Внешний	Все три
20 вершин	12 вершин	60 вершин	92 вершины
Додекаэдр	Икосаэдр	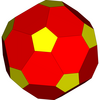Неоднородный усеченный икосаэдр	Полный икосаэдр

При рассмотрении как трехмерного твердого объекта с длиной ребер а, φа, φ²а и φ²а√2 (где φ - Золотое сечение ) полный икосаэдр имеет площадь поверхности^[10]

${\displaystyle S={\frac {1}{20}}(13211+{\sqrt {174306161}})a^{2}\,,}$

и объем^[10]

${\displaystyle V=(210+90{\sqrt {5}})a^{3}\,.}$

Как звездный многогранник

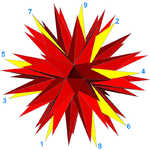Двадцать 9 граней многоугольника (одна грань нарисована желтым с 9 отмеченными вершинами).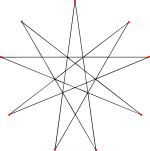

2-изогональный 9 лиц

Полную звездчатую форму можно также рассматривать как самопересекающийся звездный многогранник имеющий 20 граней, соответствующих 20 граням нижележащего икосаэдра. Каждое лицо - неправильное 9/4 звездный многоугольник, или же эннеаграмма.^[6] Поскольку три грани пересекаются в каждой вершине, он имеет 20 × 9/3 = 60 вершин (это самый внешний слой видимых вершин и образуют концы «шипов») и 20 × 9/2 = 90 ребер (каждый край ребра звездный многогранник включает и соединяет два из 180 видимых ребер).

Если рассматривать звездный икосаэдр, вся звездчатость благородный многогранник, потому что это оба равногранный (лицо-переходное) и изогональный (вершинно-транзитивный).

Смотрите также

• Многогранник Кеплера – Пуансо
• Список моделей многогранников Веннингера

Примечания

1. Coxeter et al. (1938), стр 30–31
2. Веннингер, Модели многогранников, п. 65.
3. Брюкнер, Макс (1900)
4. Вайсштейн, Эрик В. "Кеплер-Пуансо Солид". MathWorld.
5. Луи Пуансо, Воспоминания о многоугольниках и многогранниках. J. de l'École Polytechnique 9, стр. 16–48, 1810.
6. Кромвель (1999) (стр. 259)
7. Уиллер (1924)
8. Название ехиднаэдр можно приписать Эндрю Хьюму, разработчик из netlib база данных многогранников:
   «... и несколько необычных тел, включая ехиднаэдр (мое имя; на самом деле это последняя звездчатая форма икосаэдра)». geometry.research; "база данных многогранников"; 30 августа 1995 г., 12:00.
   
9. Ехиднаэдр В архиве 2008-10-07 на Wayback Machine на polyhedra.org
10. Вайсштейн, Эрик В. «Ехиднаэдр». MathWorld.

Рекомендации

• Брюкнер, Макс (1900). Vielecke und Vielflache: Theorie und Geschichte. Лейпциг: B.G. Treubner. ISBN  978-1-4181-6590-1. (на немецком) WorldCat Английский: Многоугольники и многогранники: теория и история. Фотографии моделей: Тафель VIII (табл. VIII), так далее. Высокое разрешение. сканы.
• А. Х. Уиллер, Некоторые формы икосаэдра и способ получения и обозначения высших многогранников, Proc. Междунар. Математика. Конгресс, Торонто, 1924 г., т. 1. С. 701–708.
• H.S.M. Coxeter, Правильные многогранники, (3-е издание, 1973 г.), Дуврское издание, ISBN  0-486-61480-8, 3.6 6.2 Звездчатые тела Платоновых тел, стр. 96–104
• Кокстер, Гарольд Скотт Макдональд; Du Val, P .; Flather, H.T .; Петри, Дж. Ф. (1999), Пятьдесят девять икосаэдров (3-е изд.), Тарквин, ISBN  978-1-899618-32-3, МИСТЕР  0676126 (1-й Эднский университет Торонто (1938))
• Веннингер, Магнус Дж., Модели многогранников; Издательство Кембриджского университета, 1-е изд. (1983), Ppbk (2003). ISBN  978-0-521-09859-5. (Модель 42, стр. 65, Окончательная звездчатость икосаэдра)
• Кромвель, Питер Р. (1997). Многогранники. Издательство Кембриджского университета. ISBN  0-521-66405-5.
• Дженкинс, Джеральд и Магдалина Медведь. Последняя звездчатая форма икосаэдра: продвинутая математическая модель, которую нужно вырезать и склеить. Норфолк, Англия: Tarquin Publications, 1985. ISBN  978-0-906212-48-6.

внешняя ссылка

• С инструкциями по построению модели ехиднаэдра (.doc ) Ральфом Джонсом
• К звёздчатому икосаэдру и огранке додекаэдра Гай Инчбальд
• Вайсштейн, Эрик В. «Пятьдесят девять звёздчатых икосаэдров». MathWorld.
  • Вайсштейн, Эрик В. «Ехиднаэдр». MathWorld.
• Звёздчатые формы икосаэдра
• 59 Звёздчатые формы Икосаэдра
• VRML модель: http://www.georgehart.com/virtual-polyhedra/vrml/echidnahedron.wrl
• Netlib: База данных многогранников, модель 141

Примечательный звёздчатые формы икосаэдра
Обычный	Униформа двойников			Обычные соединения			Обычная звезда	Другие
(Выпуклый) икосаэдр	Малый триамбический икосаэдр	Медиальный триамбический икосаэдр	Большой триамбический икосаэдр	Соединение пяти октаэдров	Соединение пяти тетраэдров	Соединение десяти тетраэдров	Большой икосаэдр	Раскопанный додекаэдр	Окончательная звездчатость
Процесс образования звезд на икосаэдре создает ряд связанных многогранники и соединения с икосаэдрическая симметрия.