Соотношение сторон - Aspect ratio

Для использования в других целях см. Соотношение сторон (значения).

В соотношение сторон из геометрический форма это соотношение его размеров в разных размерах. Например, соотношение сторон экрана прямоугольник это отношение его длинной стороны к короткой - отношение ширины к высоте,^[1][2] когда прямоугольник ориентирован как «пейзаж».

Соотношение сторон чаще всего выражается двумя целыми числами, разделенными двоеточием (x: y), реже - простым или десятичным числом. дробная часть. Значения x и y представляют не фактическую ширину и высоту, а скорее соотношение между шириной и высотой. Например, 8: 5, 16:10, 1,6: 1,⁸⁄₅ и 1.6 - все способы представления одного и того же соотношения сторон.

В объектах более двух измерений, таких как гипер прямоугольники, соотношение сторон можно определить как отношение самой длинной стороны к самой короткой стороне.

Приложения и использование

Этот термин чаще всего используется в отношении:

• Графика / изображение
  • Соотношение сторон изображения
  • Соотношение сторон дисплея
  • Размер бумаги
  • Стандартные форматы фотопечати
  • Форматы кинофильмов
  • Стандартный размер объявления
  • Соотношение сторон пикселей
  • Фотолитография: соотношение сторон вытравленной или осажденной структуры - это отношение высоты ее вертикальной боковой стенки к ее ширине.
• HARMST Высокое соотношение сторон позволяет создавать высокие микроструктуры без уклона.
• Код шины
• Размер шин
• Турбокомпрессор размер рабочего колеса
• Соотношение сторон крыла самолета или птицы
• Астигматизм из оптическая линза
• Размеры наностержня
• Фактор формы (анализ изображений и микроскопия)

Соотношение сторон простых форм

Прямоугольники

Основная статья: Соотношение сторон (изображение)

Для прямоугольника соотношение сторон обозначает отношение ширины к высоте прямоугольника. А квадрат имеет наименьшее возможное соотношение сторон 1: 1.

Примеры:

• 4:3 = 1.3: Некоторые (не все) компьютерные мониторы 20-го века (VGA, XGA, так далее.), телевидение стандартной четкости
• ${\displaystyle {\sqrt {2}}:1=1.414...}$: международные форматы бумаги (ISO 216 )
• 3:2 = 1.5: 35-мм фотопленка, iPhone (до того как iPhone 5 ) отображает
• 16:10 = 1,6: обычно используется широкоформатный компьютерные дисплеи (WXGA )
• Φ: 1 = 1,618 ...: Золотое сечение, близко к 16:10
• 5:3 = 1.6: супер 16 мм, стандарт пленка во многих странах Европы
• 16:9 = 1.7: широкоформатный телевидение
• 2:1 = 2: домино
• 64:27 = 2.370: сверхширокоформатный, 21:9
• 32:9 = 3.5: супер сверхширокий экран

Эллипсы

Для эллипса соотношение сторон обозначает соотношение сторон большая ось к малая ось. Эллипс с соотношением сторон 1: 1 - это круг.

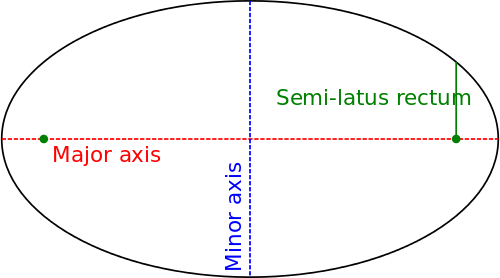
Соотношение сторон общих форм

В геометрия, есть несколько альтернативных определений соотношения сторон общего компактные наборы в d-мерном пространстве:^[3]

• Отношение диаметра к ширине (DWAR) компактного набора - это отношение его диаметра к его ширине. У круга минимальный DWAR равен 1. У квадрата есть DWAR ${\displaystyle {\sqrt {2}}}$.
• Соотношение сторон кубического объема (CVAR) компактного набора - это dкорень -й степени отношения d-объем наименьших охватывающих осей-параллельны d-куб в свой набор d-объем. Квадрат имеет минимальный CVAR, равный 1. У круга CVAR равен ${\displaystyle {\sqrt {2}}}$. Прямоугольник шириной, параллельный оси W и высота ЧАС, куда W>ЧАС, имеет CVAR ${\displaystyle {\sqrt {W^{2}/WH}}={\sqrt {W/H}}}$.

Если размер d фиксировано, то все разумные определения соотношения сторон эквивалентны с точностью до постоянных коэффициентов.

Обозначения

Соотношение сторон математически выражается как Икс:у (произносится как «х-к-у»).

Кинематографические соотношения сторон обычно обозначаются как (округленное) десятичное число, кратное ширине и единице высоты, в то время как фотографические и видеографические соотношения сторон обычно определяются и обозначаются целочисленными отношениями ширины к высоте. В цифровые изображения есть тонкое различие между отображать соотношение сторон (изображение, как показано) и место хранения соотношение сторон (соотношение размеров пикселей); видеть Отличия.

Смотрите также

• Осевое соотношение
• Соотношение
• Равномерный соотношения в 3D
• Список форматов фильмов
• Сжать карту
• Масштаб (соотношение)
• Вертикальная ориентация

Рекомендации

1. Роуз, Маргарет (сентябрь 2005 г.). "Что такое соотношение сторон?". Что?. TechTarget. Получено 3 февраля 2013.
2. Роуз, Маргарет (сентябрь 2002 г.). «Дисплей с широким соотношением сторон». отображать. E3displays. Получено 18 февраля 2020.
3. Smith, W. D .; Вормальд, Н. С. (1998). «Геометрические теоремы о разделителях и приложения». Материалы 39-го ежегодного симпозиума по основам компьютерных наук (каталожный номер 98CB36280). п. 232. Дои:10.1109 / sfcs.1998.743449. ISBN  0-8186-9172-7.