Стандартный гравитационный параметр - Standard gravitational parameter

Тело	μ [м^3 s^−2]
солнце	1.32712440018(9)×10^20[1]
Меркурий	2.2032(9)×10^13[2]
Венера	3.24859(9)×10^14
земной шар	3.986004418(8)×10^14[3]
Луна	4.9048695(9)×10^12
Марс	4.282837(2)×10^13[4]
Церера	6.26325×10^10[5][6][7]
Юпитер	1.26686534(9)×10^17
Сатурн	3.7931187(9)×10^16
Уран	5.793939(9)×10^15[8]
Нептун	6.836529(9)×10^15
Плутон	8.71(9)×10^11[9]
Эрис	1.108(9)×10^12[10]

В небесная механика, то стандартный гравитационный параметр μ из небесное тело продукт гравитационная постоянная грамм и масса M тела.

${\displaystyle \mu =GM\ }$

Для нескольких объектов в Солнечная система, значение μ известен с большей точностью, чем любой грамм или же M.^[11] В SI единицы стандартного гравитационного параметра м³ s⁻². Однако единицы км³ s⁻² часто используются в научной литературе и в навигации космических аппаратов.

Определение

Маленькое тело, вращающееся вокруг центрального тела

Связь между свойствами массы и соответствующими физическими константами. Считается, что каждый массивный объект обладает всеми пятью свойствами. Однако из-за очень больших или очень маленьких констант, как правило, невозможно проверить более двух или трех свойств для любого объекта.

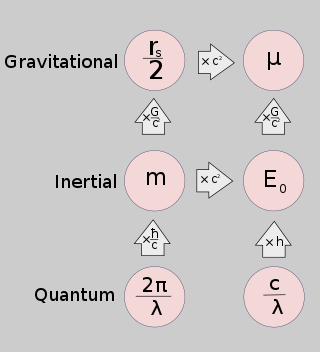
• В Радиус Шварцшильда (р_s) представляет собой способность массы вызывать искривление пространства и времени.
• В стандартный гравитационный параметр (μ) представляет собой способность массивного тела воздействовать на другие тела ньютоновскими силами тяготения.
• Инерционный масса (м) представляет собой ньютоновский отклик массы на силы.
• Энергия отдыха (E₀) представляет собой способность массы превращаться в другие формы энергии.
• В Комптоновская длина волны (λ) представляет собой квантовый отклик массы на локальную геометрию.

В центральный орган в орбитальной системе может быть определена как та, масса которой (M) намного больше, чем масса вращающееся тело (м), или же M ≫ м. Это приближение стандартно для планет, вращающихся вокруг солнце или большинство лун и значительно упрощает уравнения. Под Закон всемирного тяготения Ньютона, если расстояние между телами р, сила, действующая на меньшее тело, равна:

${\displaystyle F={\frac {GMm}{r^{2}}}={\frac {\mu m}{r^{2}}}}$

Таким образом, для предсказания движения меньшего тела необходимо только произведение G и M. И наоборот, измерения орбиты меньшего тела дают информацию только о продукте μ, а не о G и M по отдельности. Гравитационная постоянная G трудно измерить с высокой точностью.^[12] в то время как орбиты, по крайней мере в Солнечной системе, можно измерить с большой точностью и использовать для определения μ с такой же точностью.

Для круговая орбита вокруг центрального тела:

${\displaystyle \mu =rv^{2}=r^{3}\omega ^{2}={\frac {4\pi ^{2}r^{3}}{T^{2}}}\ }$

куда р это орбита радиус, v это орбитальная скорость, ω это угловая скорость, и Т это орбитальный период.

Это можно обобщить на эллиптические орбиты:

${\displaystyle \mu ={\frac {4\pi ^{2}a^{3}}{T^{2}}}\ }$

куда а это большая полуось, который Третий закон Кеплера.

За параболические траектории rv² постоянна и равна 2μ. Для эллиптических и гиперболических орбит μ = 2а|ε|, куда ε это удельная орбитальная энергия.

Общий случай

В более общем случае, когда тела не обязательно должны быть большими и маленькими, например а двойная звезда системы, мы определяем:

• вектор р положение одного тела относительно другого
• р, v, а в случае эллиптическая орбита, то большая полуось а, определены соответственно (отсюда р это расстояние)
• μ = Gm₁ + Gm₂ = μ₁ + μ₂, куда м₁ и м₂ - массы двух тел.

Потом:

• за круговые орбиты, rv² = р³ω² = 4π²р³/Т² = μ
• за эллиптические орбиты, 4π²а³/Т² = μ (с а выражено в AU; Т в годы и M общая масса относительно массы Солнца, мы получаем а³/Т² = M)
• за параболические траектории, rv² постоянна и равна 2μ
• для эллиптических и гиперболических орбит, μ в два раза больше большой полуоси, умноженной на отрицательное значение удельная орбитальная энергия, где последняя определяется как полная энергия системы, деленная на уменьшенная масса.

В маятнике

Стандартный гравитационный параметр можно определить с помощью маятник колеблется над поверхностью тела как:^[13]

${\displaystyle \mu \approx {\frac {4\pi ^{2}r^{2}L}{T^{2}}}}$

куда р - радиус гравитирующего тела, L - длина маятника, а Т это период маятника (по поводу аппроксимации см. Маятник в математике ).

Солнечная система

Дальнейшая информация: Гауссова гравитационная постоянная

Геоцентрическая гравитационная постоянная

Дальнейшая информация: Масса Земли

граммM_⊕, гравитационный параметр для земной шар как центральное тело, называется геоцентрическая гравитационная постоянная. Это равно (3.986004418±0.000000008)×10¹⁴ м³ s⁻².^[3]

Значение этой константы стало важным с началом космический полет в 1950-х годах, и в течение 1960-х годов были приложены большие усилия, чтобы определить его как можно точнее. Загитов (1969) приводит ряд значений, полученных в результате высокоточных измерений 1960-х годов, с относительной погрешностью порядка 10⁻⁶.^[14]

В течение 1970-1980-х годов все большее количество искусственные спутники на околоземной орбите дополнительно способствовало высокоточным измерениям, а относительная погрешность была уменьшена еще на три порядка, до примерно 2×10⁻⁹ (1 из 500 миллионов) по состоянию на 1992 год. Измерения включают в себя наблюдения расстояний от спутников до земных станций в разное время, которые могут быть получены с высокой точностью с помощью радара или лазерной локации.^[15]

Гелиоцентрическая гравитационная постоянная

Дальнейшая информация: Солнечная масса

граммM_☉, гравитационный параметр для солнце как центральное тело, называется гелиоцентрическая гравитационная постоянная или же геопотенциал Солнца и равно (1.32712440042±0.0000000001)×10²⁰ м³ s⁻².^[16]

Относительная неопределенность в граммM_☉, цитируется ниже 10⁻¹⁰ по состоянию на 2015 г. меньше неопределенности в граммM_⊕ потому что граммM_☉ определяется дальностью межпланетных зондов, и абсолютная погрешность измерения расстояния до них примерно такая же, как и у измерения дальности спутников Земли, в то время как абсолютные расстояния намного больше^{[нужна цитата ]}.

Смотрите также

• Астрономическая система единиц
• Планетная масса

Рекомендации

1. «Астродинамические константы». НАСА /JPL. 27 февраля 2009 г.. Получено 27 июля 2009.
2. Андерсон, Джон Д .; Коломбо, Джузеппе; Эспозито, Паскуале Б.; Lau, Eunice L .; Трагер, Гейл Б. (сентябрь 1987 г.). «Масса, гравитационное поле и эфемериды Меркурия». Икар. 71 (3): 337–349. Bibcode:1987Icar ... 71..337A. Дои:10.1016/0019-1035(87)90033-9.
3. «Числовые стандарты фундаментальной астрономии». maia.usno.navy.mil. Рабочая группа IAU. Получено 31 октября 2017.со ссылкой на Ries, J.C., Eanes, R.J., Shum, C.K. и Watkins, M.M., 1992, «Прогресс в определении гравитационного коэффициента Земли», Geophys. Res. Lett., 19 (6), стр. 529-531.
4. «Марс Гравитационная Модель 2011 (MGM2011)». Группа геодезии Западной Австралии. Архивировано из оригинал на 2013-04-10.
5. "Файл ядра SPICE астероида Ceres P_constants (PcK)". Получено 5 ноября 2015.
6. Е.В. Питьевой (2005). «Высокоточные эфемериды планет - EPM и определение некоторых астрономических констант» (PDF). Исследования Солнечной Системы. 39 (3): 176. Bibcode:2005СоСыР..39..176П. Дои:10.1007 / s11208-005-0033-2.
7. Д. Т. Бритт; Д. Йоманс; К. Хаусен; Г. Консольманьо (2002). «Плотность, пористость и структура астероидов» (PDF). У В. Боттке; А. Челлино; П. Паолички; Р.П. Бинзель (ред.). Астероиды III. Университет Аризоны Press. п. 488.
8. Р.А. Якобсон; J.K. Кэмпбелл; А. Х. Тейлор; С.П. Синнотт (1992). «Массы Урана и его основных спутников из данных слежения« Вояджер »и данных наземных спутников Урана». Астрономический журнал. 103 (6): 2068–2078. Bibcode:1992AJ .... 103.2068J. Дои:10.1086/116211.
9. M.W. Buie; W.M. Гранди; Э.Ф. Янг; Л.А. Янг; и другие. (2006). «Орбиты и фотометрия спутников Плутона: Харон, S / 2005 P1 и S / 2005 P2». Астрономический журнал. 132 (1): 290–298. arXiv:astro-ph / 0512491. Bibcode:2006AJ .... 132..290B. Дои:10.1086/504422.
10. М.Е. Браун; E.L. Шаллер (2007). «Масса карликовой планеты Эрида». Наука. 316 (5831): 1586. Bibcode:2007Научный ... 316.1585B. Дои:10.1126 / science.1139415. PMID  17569855.
11. Это в основном потому, что μ можно измерить только с помощью наблюдательной астрономии, как это было на протяжении столетий. Разъединяя его на грамм и M должны быть выполнены путем измерения силы тяжести в чувствительных лабораторных условиях, как это было впервые сделано в Кавендиш эксперимент.
12. Джордж Т. Гиллис (1997), «Ньютоновская гравитационная постоянная: недавние измерения и связанные исследования», Отчеты о достижениях физики, 60 (2): 151–225, Bibcode:1997RPPh ... 60..151G, Дои:10.1088/0034-4885/60/2/001. Длинный подробный обзор.
13. Леваль, Филипп; Димино, Тони (2014), Измерение гравитационной постоянной Земли с помощью маятника (PDF), п. 1
14. Загитов М. У. «Современное состояние определений гравитационной постоянной и массы Земли». Советская астрономия, Vol. 13 (1970), 712-718, пер. С Астрономический журнал Vol. 46, № 4 (июль – август 1969 г.), 907–915.
15. Lerch, Francis J .; Лаубшер, Рой Э .; Клоско, Стивен М .; Смит, Дэвид Э .; Коленкевич, Рональд; Путни, Барбара Х .; Марш, Джеймс Дж .; Браун, Джозеф Э. (декабрь 1978 г.). «Определение геоцентрической гравитационной постоянной по лазерной локации на околоземных спутниках». Письма о геофизических исследованиях. 5 (12): 1031–1034. Bibcode:1978GeoRL ... 5.1031L. Дои:10.1029 / GL005i012p01031.
16. Питьева, Э. В. (сентябрь 2015 г.). «Определение значения гелиоцентрической гравитационной постоянной из современных наблюдений планет и космических аппаратов». Журнал физических и химических справочных данных. 44 (3): 031210. Bibcode:2015JPCRD..44c1210P. Дои:10.1063/1.4921980.