Фазировка орбиты - Orbit phasing

Угол фазы

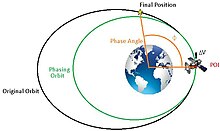В астродинамике фазировка орбиты - это корректировка временного положения космического корабля на его орбите, обычно описываемая как корректировка истинной аномалии орбитального космического корабля.^[1] Орбитальная фазировка в основном используется в сценариях, когда космический аппарат на данной орбите должен быть перемещен в другое место на той же орбите. Изменение положения на орбите обычно определяется как фазовый угол ϕ, и это изменение истинной аномалии, требуемой между текущим положением космического корабля и конечным положением.

Фазовый угол можно преобразовать во времени с помощью уравнения Кеплера:^[2]

${\displaystyle t={\frac {T_{1}}{2\pi }}(E-e_{1}\sin E)}$

${\displaystyle E=2\arctan({\sqrt {\frac {1-e_{1}}{1+e_{1}}}}\tan {\frac {\phi }{2}})}$

куда

т определяется как время, необходимое для покрытия фазового угла на исходной орбите

Т₁ определяется как период первоначальной орбиты

E определяется как изменение Эксцентрическая аномалия между космическим кораблем и конечной позицией

е₁ определяется как Орбитальный эксцентриситет исходной орбиты

Φ определяется как изменение истинная аномалия между космическим кораблем и конечной позицией

Фазовая орбита
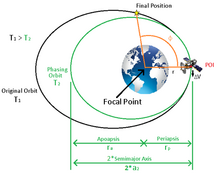Если космический корабль отстает от конечной позиции на той же орбите, космический корабль должен замедлиться, чтобы выйти на меньшую, более быструю фазирующую орбиту, чтобы догнать конечное положение.

Это время, полученное из фазового угла, и есть необходимое время, которое космический аппарат должен получить или проиграть, чтобы оказаться в конечном положении на орбите. Чтобы выиграть или проиграть это время, космический корабль должен быть подвергнут простой двухимпульсной передаче Хомана, которая уводит космический корабль с исходной орбиты, а затем обратно. Первый импульс для изменения орбиты космического корабля выполняется в определенной точке исходной орбиты (точка импульса, POI), как правило, на исходной орбите. перицентр или же апоапсис. Импульс создает новую орбиту, называемую «фазирующей орбитой», которая больше или меньше исходной орбиты, в результате чего период времени отличается от исходной орбиты. Разница во времени между исходной и фазовой орбитами будет равна времени, преобразованному из фазового угла. По завершении одного периода фазирующей орбиты космический аппарат вернется в точку POI, и космический корабль снова будет подвергнут второму импульсу, равному и противоположному первому импульсу, чтобы вернуть его на исходную орбиту. По завершении космический корабль окажется в намеченной конечной позиции в исходном некрологе.

Чтобы найти некоторые параметры фазирующей орбиты, сначала необходимо найти требуемый период фазирующей орбиты, используя следующее уравнение.

${\displaystyle T_{2}=T_{1}-t}$

куда

Т₁ определяется как период первоначальной орбиты

Т₂ определяется как период фазирования орбиты

т определяется как время, необходимое для покрытия фазового угла на исходной орбите

После определения периода фазовой орбиты фазовая орбита большая полуось может быть получено из формулы периода:^[3]

${\displaystyle a_{2}=({\frac {{\sqrt {\mu }}T_{2}}{2\pi }})^{\frac {2}{3}}}$

куда

а₂ определяется как большая полуось фазовой орбиты

Т₂ определяется как период фазирования орбиты

μ определяется как Стандартный гравитационный параметр

По большой полуоси можно рассчитать апогей и перигей фазовой орбиты:

${\displaystyle 2a_{2}=r_{a}+r_{p}}$

куда

а₂ определяется как большая полуось фазовой орбиты

р_а определяется как апогей фазовой орбиты

р_п определяется как перигей фазирующей орбиты

Наконец, угловой момент фазирующей орбиты можно найти из уравнения:

${\displaystyle h_{2}={\sqrt {2\mu }}{\sqrt {\frac {r_{a}r_{p}}{r_{a}+r_{p}}}}}$

куда

час₂ определяется как момент количества движения фазирующей орбиты

р_а определяется как апогей фазовой орбиты

р_п определяется как перигей фазирующей орбиты

μ определяется как Стандартный гравитационный параметр

Чтобы найти импульс, необходимый для изменения космического аппарата с его исходной орбиты на фазирующую орбиту, изменение скорости космического корабля,∆V, в точке POI необходимо рассчитывать по формуле момента количества движения:

${\displaystyle \Delta V=v_{2}-v_{1}={\frac {h_{2}}{r}}-{\frac {h_{1}}{r}}}$

куда

∆V изменение скорости между фазированием и исходной орбитой в точке интереса

v₁ определяется как скорость космического корабля в точке нахождения на исходной орбите.

v₂ определяется как скорость космического аппарата в точке нахождения на фазированной орбите

р определяется как радиус космического корабля от фокуса орбиты до точки интереса

час₁ определяется как угловой момент исходной орбиты

час₂ определяется как момент количества движения фазирующей орбиты

Коорбитальное рандеву
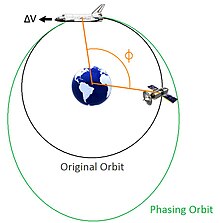Если цель (спутник) находится позади космического корабля (шаттла) на той же орбите, космический корабль должен разогнаться, чтобы выйти на большую, более медленную фазирующую орбиту, чтобы позволить цели догнать.

Помните, что это изменение скорости, ∆V, это только сумма, необходимая для перевода космического аппарата с исходной орбиты на фазирующую орбиту. Второе изменение скорости, равное величине, но противоположное по направлению первому, должно быть выполнено после того, как космический корабль пройдет один период фазовой орбиты, чтобы вернуть космический корабль с фазирующей орбиты на исходную орбиту. Общее изменение скорости, необходимое для маневра фазирования, равно двум разам. ∆V.

Фазирование орбиты также можно назвать коорбитальным сближением. ^[4] как успешный подход к космической станции в маневре стыковки. Здесь два космических аппарата на одной орбите, но с разными истинными аномалиями сближаются, когда один или оба космических корабля выходят на фазирующие орбиты, что заставляет их одновременно возвращаться на исходную орбиту с одной и той же истинной аномалией.

Фазовые маневры также обычно используются геостационарными спутниками для выполнения маневров по удержанию станции для поддержания их орбиты выше определенной долготы или для изменения долготы в целом.

Смотрите также

• Космический портал

• Орбитальный маневр
• Переходная орбита Хомана
• Уравнения Клохесси-Уилтшира для анализа совместной орбиты
• Космическое рандеву

Рекомендации

1. «Архивная копия». Архивировано из оригинал на 2013-12-16. Получено 2013-12-13.
2. Кертис, Ховард Д. (2014). Орбитальная механика для студентов инженерных специальностей (Третье издание). Баттерворт-Хайнеманн. п. 312-316. ISBN  978-0-08-097747-8.
3. Фрэнсис, Хейл Дж (1994). Введение в космический полет. Prentice-Hall, Inc .. стр. 33. ISBN  0-13-481912-8.
4. Продавцы, Джерри Джон (2005). Понимание космоса Введение в астронавтику (третье издание). Макгроу-Хилл. п. 213-214. ISBN  978-0-07-340775-3.

Общий

• Кертис, Ховард Д. (2014). Орбитальная механика для студентов инженерных специальностей (Третье изд.). Баттерворт-Хайнеманн. ISBN  978-0-08-097747-8.
• Фрэнсис, Хейл Дж (1994). Введение в космический полет. Prentice-Hall, Inc. ISBN  0-13-481912-8.
• Продавцы, Джерри Джон; Мэрион, Джерри Б. (2005). Понимание космоса Введение в астронавтику (Третье изд.). Макгроу-Хилл. ISBN  978-0-07-340775-3.
• http://arc.aiaa.org/doi/pdf/10.2514/2.6921^{[постоянная мертвая ссылка ]} Минимальное время орбитальных маневров фазирования - AIAA, CD Hall - 2003
• Фазовый маневр