Проекция (математика) - Projection (mathematics)
Эта статья не цитировать любой источники. (Октябрь 2014 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
В математика, а проекция является отображением набор (или другой математическая структура ) в подмножество (или подструктуру), которое равно его квадрату для составление карт (или, другими словами, что идемпотент ). В ограничение в подпространство проекции также называется проекция, даже если свойство идемпотентности потеряно. Обычным примером проекции является отбрасывание тени на плоскость (лист бумаги). Проекция точки - это ее тень на листе бумаги. Тень точки на листе бумаги и есть сама эта точка (идемпотентность). Тень трехмерной сферы - это замкнутый диск. Первоначально понятие проекции было введено в Евклидова геометрия для обозначения проекции Евклидово пространство трех измерений на плоскость в нем, как в примере с тенью. Двумя основными проекциями такого рода являются:
- В проекция из точки на плоскость или же центральная проекция: Если C это точка, называемая центр проекции, то проекция точки п отличается от C на плоскость, не содержащую C это пересечение линии CP с самолетом. Точки п так что линия CP параллельна плоскости не имеет никакого изображения проекцией, но часто говорят, что они проецируются в бесконечно удаленную точку плоскости (см. проективная геометрия для формализации этой терминологии). Проекция точки C сам не определяется.
- В проекция, параллельная направлению D, на плоскость или же параллельная проекция: Изображение точки п - пересечение с плоскостью прямой, параллельной D проходя через п. Видеть Аффинное пространство § Проекция для точного определения, обобщенного для любого измерения.
Концепция чего-либо проекция в математика очень старый, скорее всего, уходит корнями в феномен теней, отбрасываемых реальными объектами на землю. Эта элементарная идея была уточнена и абстрагирована сначала в геометрическом контексте, а затем в других разделах математики. Со временем развивались разные версии концепции, но сегодня, в достаточно абстрактной обстановке, мы можем объединить эти варианты.
В картография, а картографическая проекция - это карта части поверхности Земли на плоскость, которая в некоторых случаях, но не всегда, является ограничением проекции в указанном выше смысле. В 3D проекции также лежат в основе теории перспектива.
Необходимость объединения двух видов проекций и определения изображения центральной проекцией любой точки, отличной от центра проекции, лежит в основе проективная геометрия. Однако проективное преобразование это биекция проективного пространства, свойство нет поделился с прогнозы этой статьи.
Определение
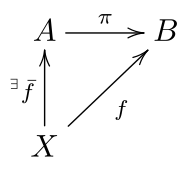
В абстрактном контексте мы обычно можем сказать, что проекция является отображением набор (или математическая структура ) который идемпотент, что означает, что проекция равна своему сочинение с собой. А проекция может также относиться к отображению, которое имеет обратный справа. Оба понятия тесно связаны между собой следующим образом. Позволять п быть идемпотентом карта из набора А в себя (таким образом п ∘ п = п) и B = п(А) быть изображением п. Если обозначить через π карта п рассматривается как карта из А на B и по я в инъекция из B в А (так что п = я ∘ π), то имеем π ∘ я = IdB (так что π имеет правую инверсию). Наоборот, если π имеет правый обратный, то π ∘ я = IdB подразумевает, что я ∘ π идемпотентно.
Приложения
Первоначальное понятие проекции было расширено или обобщено на различные математические ситуации, часто, но не всегда, связанные с геометрией, например:
- В теория множеств:
- Операция, типичная для j th карта проекции, письменный проектj , который принимает элемент Икс = (Икс1, ..., Иксj , ..., Иксk) из декартово произведение Икс1 × … × Иксj × … × Иксk к стоимости проектаj (Икс) = Иксj . Эта карта всегда сюръективный.
- Отображение, которое приводит элемент к его класс эквивалентности под данным отношение эквивалентности известен как каноническая проекция.
- Карта оценки отправляет функцию ж к значению ж(Икс) для фиксированного Икс. Пространство функций YИкс можно отождествить с декартовым произведением , а оценочная карта - это карта проекции из декартова произведения.
- За реляционные базы данных и языки запросов, то проекция это унарная операция написано как куда представляет собой набор имен атрибутов. Результат такой проекции определяется как набор что получается, когда все кортежи в р ограничены набором . р это отношение к базе данных.
- В сферическая геометрия, проекция шара на плоскость использовалась Птолемей (~ 150) в его Planisphaerium. Метод называется стереографическая проекция и использует плоскость, касательную к сфере и столб C диаметрально противоположно точке касания. Любая точка п на сфере кроме C определяет линию CP пересечение плоскости в проектируемой точке для п. Соответствие делает сферу одноточечная компактификация для самолета, когда точка в бесконечности включен, чтобы соответствовать C, который в противном случае не имеет проекции на плоскость. Распространенным примером является комплексная плоскость где компактификация соответствует Сфера Римана. В качестве альтернативы полушарие часто проецируется на плоскость с помощью гномоническая проекция.
- В линейная алгебра, а линейное преобразование который остается неизменным, если применяется дважды (п(ты) = п(п(ты))), другими словами, идемпотент оператор. Например, отображение, которое берет точку (Икс, у, z) в трех измерениях до точки (Икс, у, 0) на плоскости является проекцией. Этот тип проекции естественно обобщается на любое количество измерений. п для источника и k ≤ п для цели отображения. Видеть ортогональная проекция, проекция (линейная алгебра). В случае ортогональных проекций пространство допускает разложение как произведение, и оператор проекции также является проекцией в этом смысле.
- В дифференциальная топология, любой пучок волокон включает карту проекции как часть своего определения. По крайней мере, локально эта карта выглядит как проекционная карта в смысле топологии продукта и поэтому является открытой и сюръективной.
- В топология, а втягивание это непрерывное отображение р: Икс → Икс который ограничивается картой идентичности на его изображении. Это удовлетворяет аналогичному условию идемпотентности р2 = р и может считаться обобщением карты проекции. Изображение ретракции называется ретрактом исходного пространства. Опровержение, которое гомотопный к личности известен как ретракция деформации. Этот термин также используется в теории категорий для обозначения любого расщепленного эпиморфизма.
- В скалярная проекция (или решительный) одного вектор на другой.
- В теория категорий, указанное выше понятие декартового произведения множеств можно обобщить на произвольные категории. В товар некоторых объектов имеет каноническая проекция морфизм к каждому фактору. Эта проекция примет множество форм в разных категориях. Проекция из Декартово произведение из наборы, то топология продукта из топологические пространства (что всегда сюръективно и открыто ) или из прямой продукт из группы и т. д. Хотя эти морфизмы часто эпиморфизмы и даже сюръективными они не должны быть.
дальнейшее чтение
- Томас Крейг (1882) Трактат о проекциях из университет Мичигана Исторический математический сборник.




