Споры об исчислении Лейбница – Ньютона - Leibniz–Newton calculus controversy

Статуи Исаака Ньютона и Готфрида Вильгельма Лейбница во дворе Музей естественной истории Оксфордского университета, коллаж

В споры о исчислении (Немецкий: Prioritätsstreit, "приоритетный спор") был спор между математики Исаак Ньютон и Готфрид Вильгельм Лейбниц над тем, кто первым изобрел исчисление. Этот вопрос был серьезным интеллектуальным спором, который разгорелся в 1699 году и разгорелся в полную силу в 1711 году. Лейбниц первым опубликовал свою работу, но сторонники Ньютона обвинили Лейбница в плагиате неопубликованных идей Ньютона. Лейбниц умер в немилости в 1716 году после того, как его покровитель, курфюрст Георг Людвиг Ганноверский, стал Король Георг I Великобритании в 1714 году. Современное мнение состоит в том, что эти двое мужчин разработали свои идеи независимо.

Ньютон утверждал, что начал работу над формой исчисления (которую он назвал "метод флюсов и флюентов ") в 1666 году, в возрасте 23 лет, но не опубликовал его, за исключением небольшой аннотации в конце одной из своих публикаций десятилетия спустя (соответствующая рукопись Ньютона от октября 1666 года теперь опубликована среди его математических статей.[1]). Готфрид Лейбниц начал работать над своим вариантом исчисления в 1674 году, а в 1684 году опубликовал свою первую статью, в которой он использовался ».Nova Methodus pro Maximis et Minimis ". L'Hôpital опубликовал текст по исчислению Лейбница в 1696 г. (в котором он признал, что Principia 1687 г. был «почти полностью посвящен этому исчислению»). Между тем, Ньютон, хотя и объяснил свою (геометрическую) форму исчисления в Разделе I Книги I Principia 1687 г.,[2] не объяснил его возможный текучий обозначение для исчисления[3] в печати до 1693 г. (частично) и 1704 г. (полностью).

Научный приоритет в 17 веке

В XVII веке, как и в настоящее время, вопрос о научный приоритет имел большое значение для ученых. Однако в этот период научные журналы только начали появляться, а общепринятый механизм фиксации приоритета путем публикации информации об открытии еще не сформировался. Среди методов, использованных учеными, были: анаграммы, запечатанные конверты, помещенные в безопасное место, переписка с другими учеными или личное сообщение. Письмо основателю Французская Академия Наук, Марин Мерсенн для французского ученого или секретаря Лондонское королевское общество, Генри Ольденбург для английского практически имеет статус опубликованной статьи. Первооткрыватель, помимо обретения славы, избавился от необходимости доказывать, что его результат не был получен с помощью плагиат. Также практическое значение могло иметь приоритет, если бы оно было связано с изобретением новых технических устройств. Широко распространенная стратегия нападения на приоритет заключалась в том, чтобы объявить открытие или изобретение не главным достижением, а всего лишь улучшением, используя известные всем техники и, следовательно, не требующие значительного мастерства их автора.[4]

С этим именем связана серия громких споров о научном приоритете 17 века - эпохи, которую американский историк науки Д. Мели назвал «золотым веком грязных споров о приоритетах». Лейбниц. Первый из них произошел в начале 1673 года, во время его первого визита в Лондон, когда в присутствии известного математика Джон Пелл он представил свой метод аппроксимация ряда разностями. На замечание Пелла, что это открытие уже было сделано Франсуа Рено и опубликовано в 1670 году в Лион к Габриэль Мутон - ответил Лейбниц на следующий день.[5][6] В письме в Ольденбург он написал, что, просмотрев книгу Мутона, он признает, что Пелл был прав, но в свою защиту он может предоставить свои черновые записи, которые содержат нюансы, не обнаруженные Рено и Мутоном. Таким образом, была доказана честность Лейбница, но в данном случае его вспомнили позже.[7][8] Во время того же визита в Лондон Лейбниц был в противоположной позиции. 1 февраля 1673 г. на заседании Лондонского королевского общества он продемонстрировал свое механический калькулятор. Куратор экспериментов Общества Роберт Хук внимательно осмотрел устройство и даже снял для этого заднюю крышку. Несколько дней спустя, в отсутствие Лейбница, Хук раскритиковал машину немецкого ученого, заявив, что он может сделать более простую модель. Лейбниц, узнав об этом, вернулся в Париж и категорически отверг утверждение Гука в письме в Ольденбург и сформулировал принципы правильного научного поведения: «Мы знаем, что респектабельные и скромные люди предпочитают, когда они думают о чем-то, что согласуется с тем, что кто-то сделал. другие открытия приписывают первооткрывателю свои собственные улучшения и дополнения, чтобы не вызывать подозрений в интеллектуальной нечестности, и стремление к истинной щедрости должно преследовать их вместо лживой жажды нечестной выгоды ". Чтобы проиллюстрировать правильное поведение, Лейбниц приводит пример Николя-Клод Фабри де Пайреск и Пьер Гассенди, который выполнил астрономические наблюдения, аналогичные тем, которые ранее проводил Галилео Галилей и Иоганнес Гевелиус, соответственно. Узнав, что они не сделали свои открытия первыми, французские ученые передали свои данные первооткрывателям.[9]

Подход Ньютона к проблеме приоритета можно проиллюстрировать на примере открытия закон обратных квадратов применительно к динамике тел, движущихся под действием сила тяжести. На основе анализа Законы Кеплера и его собственные расчеты, Роберт Гук сделал предположение, что движение в таких условиях должно происходить по орбитам, подобным эллиптический. Не имея возможности строго доказать это утверждение, он сообщил об этом Ньютону. Не вступая далее в переписку с Гуком, Ньютон решил эту проблему, а также обратную к ней, доказав, что закон обратных квадратов следует из эллиптичности орбит. Это открытие было изложено в его знаменитой работе. Philosophiæ Naturalis Principia Mathematica без указания имени Гук. По настоянию астронома Эдмунд Галлей, которому рукопись была передана для редактирования и публикации, в текст была включена фраза о том, что соответствие первого закона Кеплера закону обратных квадратов «независимо подтверждено Крапивник, Гук и Галлей ".[10]

По замечанию Владимир Арнольд Ньютон, выбирая между отказом в публикации своих открытий и постоянной борьбой за приоритет, выбрал оба из них. [11]


Фон

Изобретение дифференциального и интегрального исчисления

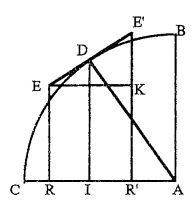
Основная статья: История исчисления
Дифференциальный треугольник Паскаля

Ко времени Ньютона и Лейбница европейские математики уже внесли значительный вклад в формирование идей математического анализа. Голландец Саймон Стевин (1548-1620), итальянец Лука Валерио (1553-1618), немец Иоганн Кеплер (1571-1630) занимались разработкой античных "метод истощения »для расчета площадей и объемов. На идеи последнего, видимо, повлияли - прямо или через Галилео Галилей - на "метод неделимых " разработан Бонавентура Кавальери (1598-1647).[12]

Последние годы жизни Лейбница, 1710–1716 гг., Были озлоблены долгими спорами с Джон Кейл, Ньютон и другие, о том, открыл ли Лейбниц исчисление независимо от Ньютона, или он просто изобрел другую систему обозначений для идей, которые в основе своей принадлежали Ньютону. Ни один участник не сомневался, что Ньютон уже разработал свой метод флюсии когда Лейбниц начал работать над дифференциальным исчислением, по-видимому, не было никаких доказательств, кроме слов Ньютона. Он опубликовал расчет касательной с примечанием: «Это только частный случай общего метода, с помощью которого я могу рассчитывать кривые и определять максимумы, минимумы и центры тяжести». Как это было сделано, он объяснил ученику целых 20 лет спустя, когда статьи Лейбница уже были начитаны. Рукописи Ньютона стали известны только после его смерти.

Исчисление бесконечно малых может быть выражено либо в нотации флюксий, либо в нотации дифференциалы, или, как отмечалось выше, это было также выражено Ньютоном в геометрической форме, как в Principia 1687 г. Ньютон использовал флюксии еще в 1666 г., но не публиковал отчет о своих обозначениях до 1693 г. Самое раннее использование дифференциалов в записных книжках Лейбница можно проследить до 1675 г. Он использовал это обозначение в письме 1677 г. Ньютону. Дифференциальная запись также появилась в мемуарах Лейбница 1684 года.

Утверждение, что Лейбниц изобрел исчисление независимо от Ньютона, основывается на том, что Лейбниц:

  1. опубликовал описание своего метода за несколько лет до того, как Ньютон напечатал что-либо о флюксиях,
  2. всегда называл это открытие его собственным изобретением (это утверждение оставалось неизменным в течение нескольких лет),
  3. пользовался сильным предположением, что действовал добросовестно, и
  4. продемонстрировал в своих частных статьях свое развитие идей исчисления способом, независимым от пути, избранного Ньютоном.

По словам недоброжелателей Лейбница, тот факт, что претензии Лейбница не оспаривались в течение нескольких лет, несущественен. Чтобы опровергнуть этот случай, достаточно показать, что он:

  • видел некоторые работы Ньютона по этому поводу до 1675 года или до 1677 года, и
  • получил основные идеи исчисления из этих работ.

Не было предпринято никаких попыток опровергнуть № 4, который не был известен в то время, но который предоставляет наиболее убедительные доказательства того, что Лейбниц пришел к исчислению независимо от Ньютона. Это свидетельство, однако, все еще вызывает сомнения на основании открытия, сделанного в ходе расследования и после того, что Лейбниц как задним числом, так и изменил основы своих «оригинальных» заметок, не только в этом интеллектуальном конфликте, но и в нескольких других.[13] Он также опубликовал «анонимные» клеветы на Ньютона относительно их разногласий, в которых он сначала пытался заявить, что не является автором.[13]

Однако, если все же предполагается добросовестность, записи Лейбница, представленные в ходе дознания, первыми оказались интеграция, который он видел как обобщение суммирования бесконечных рядов, тогда как Ньютон начал с производных. Однако, если рассматривать развитие исчисления как полностью независимое от работ Ньютона и Лейбница, упускается из виду, что оба они имели некоторое представление о методах друг друга (хотя Ньютон действительно разработал большинство основных принципов до того, как начал Лейбниц) и фактически работали вместе над несколько аспектов, в частности степенной ряд, как показано в письме к Генри Ольденбург от 24 октября 1676 г., где Ньютон отмечает, что Лейбниц разработал ряд методов, один из которых был для него новым.[14] И Лейбниц, и Ньютон могли видеть из этого обмена письмами, что другой был далеко продвинулся к исчислению (Лейбниц, в частности, упоминает об этом), но только Лейбниц тем самым подтолкнул к публикации.

То, что Лейбниц видел некоторые рукописи Ньютона, всегда было вероятным. В 1849 г. К. И. Герхардт, просматривая рукописи Лейбница, нашел выдержки из De Analysi per Equationes Numero Terminorum Infinitas (опубликовано в 1704 г. в составе De Quadratura Curvarum но также ранее распространялся среди математиков, начиная с Ньютона, давшего копию Исаак Барроу в 1669 году, и Барроу отправил его в Джон Коллинз[15]) почерком Лейбница, о существовании которого ранее не подозревали, вместе с примечаниями, повторно выражающими содержание этих отрывков в дифференциальной нотации Лейбница. Следовательно, когда эти экстракты были сделаны, становится очень важным. Известно, что копия рукописи Ньютона была отправлена ​​в Эренфрид Вальтер фон Чирнхаус в мае 1675 года, когда он и Лейбниц сотрудничали; не исключено, что эти выписки были сделаны тогда. Также возможно, что они были сделаны в 1676 году, когда Лейбниц обсуждал анализ, проведенный бесконечная серия с Коллинзом и Ольденбургом. Вполне вероятно, что тогда они показали бы ему рукопись Ньютона на эту тему, копия которой наверняка была у одного или обоих. С другой стороны, можно предположить, что Лейбниц сделал выдержки из печатной копии в 1704 году или после него. Незадолго до своей смерти Лейбниц признался в письме к Аббат Антонио Шинелла Конти, что в 1676 году Коллинз показал ему некоторые работы Ньютона, но Лейбниц также подразумевал, что они мало или совсем не представляют ценности. Предположительно, он имел в виду письма Ньютона от 13 июня и 24 октября 1676 г., а также письмо от 10 декабря 1672 г. о методе касательные, выписки из которого сопровождались письмом от 13 июня.

Использовал ли Лейбниц рукопись, из которой он скопировал отрывки, или он ранее изобрел исчисление, - это вопросы, по которым в настоящее время нет прямых доказательств. Однако стоит отметить, что неопубликованные Портсмутские документы показывают, что, когда Ньютон в 1711 году внимательно рассмотрел весь спор, он выбрал эту рукопись как рукопись, которая, вероятно, каким-то образом попала в руки Лейбница. В то время не было прямых доказательств того, что Лейбниц видел рукопись Ньютона до того, как она была напечатана в 1704 году; следовательно, гипотеза Ньютона не была опубликована. Но открытие Герхардтом копии, сделанной Лейбницем, подтверждает ее точность. Те, кто сомневается в добросовестности Лейбница, утверждают, что для человека с его способностями рукопись, особенно если она была дополнена письмом от 10 декабря 1672 г., была достаточной, чтобы дать ему ключ к пониманию методов вычисления. Поскольку рассматриваемая работа Ньютона действительно использовала флюксионную нотацию, любому, кто опирается на эту работу, пришлось бы изобрести нотацию, но некоторые это отрицают.

Разработка

Ссора была ретроспективным делом. В 1696 году, уже через несколько лет после событий, ставших предметом ссоры, позиция все еще выглядела потенциально мирной: Ньютон и Лейбниц ограниченно признали работу друг друга, а книгу Л'Опиталь 1696 года об исчислении, написанную одним из лейбницевцев. Точка зрения также признала опубликованную работу Ньютона 1680-х годов как «почти все об этом исчислении» («Presque tout de ce Calcul"), отдавая предпочтение удобству Обозначения Лейбница.[3]

Сначала не было оснований подозревать добросовестность Лейбница. В 1699 г. Николя Фатио де Дуйе, швейцарский математик, известный своими работами по проблеме зодиакального света, обвинил Лейбница в плагиат Ньютон.[16] Лишь в 1704 г. был опубликован анонимный обзор трактата Ньютона о квадратура, обзор, подразумевающий, что Ньютон заимствовал идею флюксного исчисления у Лейбница, что любой ответственный математик сомневался, что Лейбниц изобрел исчисление независимо от Ньютона. Что касается обзора квадратурной работы Ньютона, все признают, что не было никакого оправдания или авторитета для сделанных в ней утверждений, которые справедливо приписывались Лейбницу. Но последующее обсуждение привело к критическому рассмотрению всего вопроса, и возникли сомнения. Унаследовал ли Лейбниц основную идею исчисления от Ньютона? Дело против Лейбница, как казалось друзьям Ньютона, было подытожено в Commercium Epistolicum 1712 г., в котором упоминались все обвинения. Этот документ был тщательно обработан Ньютоном.

Такого резюме (с фактами, датами и ссылками) по делу Лейбница его друзья не опубликовали; но Иоганн Бернулли попытался косвенно ослабить свидетельство, нападая на личный характер Ньютона в письме от 7 июня 1713 года. Когда Бернулли настаивал на объяснении, он самым торжественным образом отрицал, что написал это письмо. Принимая опровержение, Ньютон добавил в частном письме Бернулли следующие замечания, заявленные Ньютоном причины его участия в споре. Он сказал: «Я никогда не цеплялся за славу среди чужих народов, но я очень хочу сохранить свой честолюбивый характер, который автор этого послания, как будто авторитетом великого судьи, пытался вырвать у меня. Теперь, когда я состарился, я мало получаю удовольствия от математических занятий и никогда не пытался распространять свои мнения по всему миру, но я скорее позаботился о том, чтобы не ввязываться в споры из-за них ".

Лейбниц в письме Конти от 9 апреля 1716 г. объяснил свое молчание следующим образом:

Чтобы ответить по пунктам на все работы, опубликованные против меня, мне пришлось бы вдаваться в множество мелочей, имевших место тридцать, сорок лет назад, из которых я мало что помню: мне пришлось бы поискать свои старые письма, многие из которых потерял. Более того, в большинстве случаев у меня не было копии, а когда я держал, копия закопана в огромную кучу бумаг, с которыми я мог разобраться только со временем и терпением. Я получил мало удовольствия от досуга, так как в последнее время был так загружен занятиями совершенно иного характера.

Хотя смерть Лейбница временно положила конец спорам, споры продолжались много лет.

Для стойких сторонников Ньютона это был случай, когда Лейбниц сказал, что противоречит ряду противоречивых и подозрительных деталей. Его непризнанное владение копией части одной из рукописей Ньютона можно объяснить; но оказывается, что не раз Лейбниц намеренно изменял или добавлял важные документы (например, письмо от 7 июня 1713 г. Charta Volans, а от 8 апреля 1716 г. Acta Eruditorum ), прежде чем опубликовать их, и сфальсифицировал дату на рукописи (1675 год заменен на 1673 год). Все это ставит под сомнение его показания.

Принимая во внимание интеллектуальную доблесть Лейбница, продемонстрированную другими его достижениями, он обладал более чем необходимой способностью изобрести математические вычисления. То, что он якобы получил, было скорее рядом предложений, чем отчетом о расчетах; возможно, поскольку он не публиковал свои результаты за 1677 г. до 1684 г. и поскольку дифференциальная система обозначений была его изобретением, Лейбниц через 30 лет свел к минимуму любую выгоду, которую он мог бы получить от чтения рукописи Ньютона. Более того, он, возможно, считал вопрос о том, кто создал исчисление, несущественным, если сравнивать его с выразительной силой его обозначений.

В любом случае предвзятость в пользу Ньютона с самого начала испортила все дело. В Королевское общество, президентом которой в то время был Исаак Ньютон, в ответ на письмо, полученное от Лейбница, учредили комитет для вынесения решения по спору о приоритете. Этот комитет никогда не просил Лейбница дать свою версию событий. Отчет комитета, вынесенный в пользу Ньютона, был написан и опубликован Ньютоном как «Commercium Epistolicum» (упомянутый выше) в начале 1713 года. Но Лейбниц не видел его до осени 1714 года.

Преобладающее мнение в 18 веке было против Лейбница (в Великобритании, а не в немецкоязычном мире). Сегодня все согласны с тем, что Лейбниц и Ньютон независимо изобрели и описали исчисление в Европе в 17 веке.

Безусловно, Исаак Ньютон первым изобрел новое исчисление бесконечно малых и превратил его в широко расширяемый алгоритм, возможности которого он полностью понимал; равная достоверность, дифференциальное и интегральное исчисление, кладезь великих достижений, непрерывно текущих с 1684 года до наших дней, был независимо создан Готфридом Лейбницем.

— Зал 1980: 1

Один автор назвал спор о «совершенно разных» методах:

Несмотря на… точки сходства, методы [Ньютона и Лейбница] глубоко различаются, поэтому делать приоритетную строку бессмысленным.

— Граттан-Гиннесс 1997: 247

С другой стороны, другие авторы подчеркивали эквивалентность и взаимную переводимость методов: здесь N Guicciardini (2003), похоже, подтверждает L'Hôpital (1696) (уже цитируется):

школы Ньютона и Лейбница разделяли общий математический метод. Они приняли два алгоритма, аналитический метод флюксий, а также дифференциальное и интегральное исчисление, которые можно было преобразовать один в другой.

— Гвиччардини 2003, стр. 250[17]

Ссылки в художественной литературе

Споры о математических вычислениях - главная тема в Нил Стивенсон набор исторические романы Барочный цикл (2003–04).

Антагонистический характер спора играет роль в Грег Киз Стимпанк из серии альтернативной истории Эпоха безрассудства.

Кратко упоминается Уолтер Бишоп в Сезон 1 серия из Челка, озаглавленный "Уравнение ".

На самом деле это не так уж и удивительно. Любопытные умы часто сходятся на одном и том же. Ньютон и Лейбниц независимо друг от друга, не зная друг друга, изобрели исчисление. Соответствующий вопрос: что это?

Это противоречие упоминается в записи третьего сезона Эпические рэп-баталии истории с участием Исаак Ньютон (изображаемый "Странный Эл" Янкович ) выполнение рэп баттл против Билл Най (Хороший Питер ) и Нил де Грасс Тайсон (Чали 2на ). Тайсон произносит рэп, в котором говорится, что Ньютон был занят «вонзанием кинжалов в Лейбница».

В эпизоде Теория большого взрыва[который? ], Леонарда обвиняют в том, что он не хотел бюст Исаак Ньютон в верхней части Рождественская елка Шелдоном, говоря, что это потому, что он человек Лейбница.

Смотрите также

Рекомендации

  1. ^ Д. Т. Уайтсайд (редактор), Математические статьи Исаака Ньютона (Том 1), (Cambridge University Press, 1967), часть 7 «Октябрьский трактат 1666 года о флюксиях», на странице 400, перепечатка 2008 г..
  2. ^ Раздел I Книги I Principia, объясняя «метод первых и последних отношений», геометрическую форму исчисления бесконечно малых, признанную как во времена Ньютона, так и в наше время - см. цитаты выше Л'Оспиталя (1696), Трусделла (1968) и Уайтсайда (1970) - доступен онлайн в английском переводе 1729 г., на странице 41.
  3. ^ а б Маркиз де л'Опиталь оригинальные слова о «Началах»: «lequel est presque tout de ce calc»: см. предисловие к его Анализируйте des Infiniment Petits (Париж, 1696 г.). В Principia также в наше время называли «книгой, насыщенной теорией и применением исчисления бесконечно малых»: см. Clifford Truesdell, Очерки истории механики (Берлин, 1968), стр. 99; аналогичную точку зрения другого современного ученого см. также Уайтсайд, Д. Т. (1970). «Математические принципы, лежащие в основе Principia Mathematica Ньютона». Журнал истории астрономии. 1 (2): 116–138, особенно на стр. 120. Bibcode:1970JHA ..... 1..116Вт. Дои:10.1177/002182867000100203.
  4. ^ Мели Д. Б. (1993). Эквивалентность и приоритет: Ньютон против Лейбница: включая неопубликованные рукописи Лейбница о Началах. Кларендон Пресс. п. 4. ISBN  0-19-850143-9.
  5. ^ http://www.math.rutgers.edu/courses/436/Honors02/leibniz.html
  6. ^ Николас Джолли, Лейбниц (2005), стр. 17.
  7. ^ Отчет Ольденбурга об этом инциденте содержится в бумагах Ньютона, но неизвестно, придавал ли он ему значение.
  8. ^ Зал 1980, п. 55.
  9. ^ Мели 1993, стр. 5–6.
  10. ^ Арнольд 1989 С. 16—20.
  11. ^ Арнольд 1989, п. 33.
  12. ^ Бойер 1949 С. 99—112.
  13. ^ а б Бланк, Брайан Э. (май 2009 г.). «Исчислительные войны, обзор Брайана Э. Бланка» (PDF). Уведомления Американского математического общества. 56 (5): 602–610.
  14. ^ Рукопись, написанная преимущественно на латыни, имеет номер Add. 3977,4; он содержится в библиотеке Кембриджского университета. Видеть эта страница Больше подробностей.
  15. ^ Гьертсен, Д. (1986). Справочник Ньютона. Лондон: Рутледж и Кеган Пол. п. 149.
  16. ^ Г. В. Койн, стр. 112; Руперт Холл, Философы на войне, страницы 106–107; Дэвид Брюстер, Жизнь сэра Исаака Ньютона, стр. 185
  17. ^ Никколо Гвиччардини, "Чтение принципов: дебаты о математических методах Ньютона для естественной философии с 1687 по 1736 год", (Cambridge University Press, 2003), на странице 250.

Источники

внешняя ссылка