Метод Гойнса - Heuns method

В математика и вычислительная наука, Метод Хойна может относиться к улучшенный^[1] или же модифицированный метод Эйлера (это явное правило трапеции^[2]), или аналогичный двухступенчатый Метод Рунге – Кутты. Он назван в честь Карл Хойн и является числовой процедура решения обыкновенные дифференциальные уравнения (ODE) с заданным Первоначальный значение. Оба варианта можно рассматривать как расширение Метод Эйлера в двухэтапные методы Рунге – Кутты второго порядка.

Процедура расчета численного решения начальной задачи:

${\displaystyle y'(t)=f(t,y(t)),\qquad \qquad y(t_{0})=y_{0},}$

с помощью метода Хойна - сначала вычислить промежуточное значение ${\displaystyle {\tilde {y}}_{i+1}}$ а затем окончательное приближение ${\displaystyle y_{i+1}}$ в следующей точке интеграции.

${\displaystyle {\tilde {y}}_{i+1}=y_{i}+hf(t_{i},y_{i})}$

${\displaystyle y_{i+1}=y_{i}+{\frac {h}{2}}[f(t_{i},y_{i})+f(t_{i+1},{\tilde {y}}_{i+1})],}$

куда ${\displaystyle h}$ это размер шага и ${\displaystyle t_{i+1}=t_{i}+h}$.

Описание

Метод Эйлера лежит в основе метода Хойна. Метод Эйлера использует касательную к функции в начале интервала в качестве оценки наклона функции на интервале, предполагая, что, если размер шага мал, ошибка будет небольшой. Однако даже при использовании очень малых размеров шага на большом количестве шагов начинает накапливаться ошибка, и оценка расходится с фактическим функциональным значением.

Если кривая решения вогнута вверх, ее касательная линия будет недооценивать вертикальную координату следующей точки, и наоборот для решения вогнутой вниз. Идеальная линия прогноза попадет в кривую в следующей прогнозируемой точке. На самом деле нет способа узнать, является ли решение вогнутым или вогнутым вниз, и, следовательно, будет ли следующая предсказанная точка переоценена или недооценена его вертикальное значение. Вогнутость кривой также не может быть гарантирована, чтобы оставаться согласованной, и прогноз может переоценивать или недооценивать в разных точках области решения. Метод Хеуна решает эту проблему, рассматривая интервал, охватываемый сегментом касательной прямой в целом. В примере с вогнутой вверх линия прогнозирования касательной к левому краю занижает наклон кривой для всей ширины интервала от текущей точки до следующей прогнозируемой точки. Если рассматривать касательную в правой конечной точке (которую можно оценить с помощью метода Эйлера), возникает противоположная проблема.^[3]Точки, расположенные вдоль касательной к левой конечной точке, имеют вертикальные координаты, которые недооценивают те, которые лежат на кривой решения, включая правую конечную точку рассматриваемого интервала. Решение состоит в том, чтобы немного увеличить уклон. Метод Хойна рассматривает касательные линии к кривой решения в точке обе концы интервала, тот, который переоценивает, и тот, который недооценивает идеальные вертикальные координаты. Линия прогноза должна быть построена только на основе наклона касательной к правой конечной точке, аппроксимированной с использованием метода Эйлера. Если этот наклон проходит через левую конечную точку интервала, результат, очевидно, будет слишком крутым, чтобы его можно было использовать в качестве идеальной линии прогноза, и переоценка идеальной точки. Следовательно, идеальная точка находится примерно посередине между ошибочной переоценкой и недооценкой, средним из двух наклонов.

Диаграмма, изображающая использование метода Хойна для поиска менее ошибочного прогноза по сравнению с методом Эйлера более низкого порядка

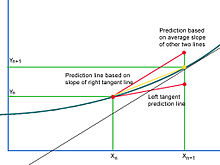
Метод Эйлера используется для грубой оценки координат следующей точки в решении, и с этим знанием исходная оценка повторно предсказывается или исправлено.^[4] Предполагая, что количество ${\displaystyle \textstyle f(x,y)}$ в правой части уравнения можно рассматривать как наклон решения, искомого в любой точке ${\displaystyle \textstyle (x,y)}$, это можно объединить с оценкой Эйлера для следующей точки, чтобы получить наклон касательной в правой конечной точке. Затем используется среднее значение обоих уклонов для нахождения исправленных координат правого конечного интервала.

Вывод

${\displaystyle {\text{Slope}}_{\text{left}}=f(x_{i},y_{i})}$

${\displaystyle {\text{Slope}}_{\text{right}}=f(x_{i}+h,y_{i}+hf(x_{i},y_{i}))}$

${\displaystyle {\text{Slope}}_{\text{ideal}}=(1/2)({\text{Slope}}_{\text{left}}+{\text{Slope}}_{\text{right}})}$

Используя принцип, согласно которому наклон линии равен подъему / спуску, координаты в конце интервала можно найти по следующей формуле:

${\displaystyle {\text{Slope}}_{\text{ideal}}={\frac {\Delta y}{h}}}$

${\displaystyle \Delta y=h({\text{Slope}}_{\text{ideal}})}$

${\displaystyle x_{i+1}=x_{i}+h}$, ${\displaystyle \textstyle y_{i+1}=y_{i}+\Delta y}$

${\displaystyle y_{i+1}=y_{i}+h{\text{Slope}}_{\text{ideal}}}$

${\displaystyle y_{i+1}=y_{i}+{\frac {1}{2}}h({\text{Slope}}_{\text{left}}+{\text{Slope}}_{\text{right}})}$

${\displaystyle y_{i+1}=y_{i}+{\frac {h}{2}}(f(x_{i},y_{i})+f(x_{i}+h,y_{i}+hf(x_{i},y_{i})))}$

Точность метода Эйлера улучшается только линейно с уменьшением размера шага, тогда как метод Хойна улучшает точность квадратично.^[5] Схему можно сравнить с скрытый трапециевидный метод, но с ${\displaystyle f(t_{i+1},y_{i+1})}$ заменен на ${\displaystyle f(t_{i+1},{\tilde {y}}_{i+1})}$ чтобы сделать это явным. ${\displaystyle {\tilde {y}}_{i+1}}$ является результатом одного шага Метод Эйлера по той же задаче начального значения. Итак, метод Хойна - это метод предиктора-корректора с форвардом Метод Эйлера как предсказатель и трапециевидный метод как корректор.

Метод Рунге – Кутты

Усовершенствованный метод Эйлера представляет собой двухэтапный Метод Рунге – Кутты, и может быть записан с использованием Таблица мясника (после Джон С. Батчер ):

	0
	1	1
		1/2	1/2

Другой метод, называемый методом Хойна (также известный как метод Ральстона), имеет таблицу Мясника:^[6]

	0
	2/3	2/3
		1/4	3/4

Этот метод минимизирует ошибку усечения.

Рекомендации

1. Сули, Эндре; Майерс, Дэвид (2003), Введение в численный анализ, Издательство Кембриджского университета, ISBN  0-521-00794-1.
2. Ascher, Uri M .; Петцольд, Линда Р. (1998), Компьютерные методы решения обыкновенных дифференциальных и дифференциально-алгебраических уравнений, Филадельфия: Общество промышленной и прикладной математики, ISBN  978-0-89871-412-8.
3. «Численные методы решения дифференциальных уравнений». Колледж Сан-Хоакин Дельта. Архивировано из оригинал на 2009-02-12.
4. Chen, Wenfang .; Ки, Дэниел Д. (2003), Высшая математика для инженерии и науки, Массачусетс, США: World Scientific, ISBN  981-238-292-5.
5. «Метод Эйлера-Хойна» (PDF). LiveToad.org. Архивировано из оригинал (PDF) на 2018-10-14.
6. Лидер, Джеффри Дж. (2004), Численный анализ и научные вычисления, Бостон: Эддисон-Уэсли, ISBN  0-201-73499-0.