Формула обратной дифференциации - Backward differentiation formula

В формула обратного дифференцирования (BDF) - это семейство неявных методов для численное интегрирование обыкновенных дифференциальных уравнений. Они есть линейные многоступенчатые методы чтобы для данной функции и времени аппроксимировать производную этой функции, используя информацию из уже вычисленных моментов времени, тем самым увеличивая точность приближения. Эти методы особенно используются для решения жесткие дифференциальные уравнения. Впервые методы были представлены Чарльз Ф. Кертисс и Джозеф О. Хиршфельдер в 1952 г.^[1]

Общая формула

BDF используется для решения проблема начального значения

${\displaystyle y'=f(t,y),\quad y(t_{0})=y_{0}.}$

Общая формула для BDF может быть записана как ^[2]

${\displaystyle \sum _{k=0}^{s}a_{k}y_{n+k}=h\beta f(t_{n+s},y_{n+s}),}$

куда ${\displaystyle h}$ обозначает размер шага и ${\displaystyle t_{n}=t_{0}+nh}$. С ${\displaystyle f}$ оценивается для неизвестного ${\displaystyle y_{n+s}}$, Методы BDF скрытый и, возможно, потребуют решения нелинейных уравнений на каждом шаге. Коэффициенты ${\displaystyle a_{k}}$ и ${\displaystyle \beta }$ выбираются так, чтобы метод достигал порядка ${\displaystyle s}$, что является максимально возможным.

Вывод коэффициентов

Исходя из формулы ${\textstyle y'(t_{n+s})=f(t_{n+s},y(t_{n+s}))}$ один приближается ${\displaystyle y(t_{n+s})\approx y_{n+s}}$ и ${\displaystyle y'(t_{n+s})\approx p_{n,s}'(t_{n+s})}$, куда ${\displaystyle p_{n,s}(t)}$ это Интерполяционный полином Лагранжа для очков ${\displaystyle (t_{n},y_{n}),\ldots ,(t_{n+s},y_{n+s})}$. Используя это ${\displaystyle t_{n}=t_{0}+nh}$ и умножение на ${\displaystyle h}$ приходит метод заказа BDF ${\displaystyle s}$.

Конкретные формулы

В s-шаговые BDFs с s <7 являются:^[3]

• BDF1: ${\displaystyle y_{n+1}-y_{n}=hf(t_{n+1},y_{n+1})}$ (это обратный метод Эйлера )
• BDF2: ${\displaystyle y_{n+2}-{\tfrac {4}{3}}y_{n+1}+{\tfrac {1}{3}}y_{n}={\tfrac {2}{3}}hf(t_{n+2},y_{n+2})}$
• BDF3: ${\displaystyle y_{n+3}-{\tfrac {18}{11}}y_{n+2}+{\tfrac {9}{11}}y_{n+1}-{\tfrac {2}{11}}y_{n}={\tfrac {6}{11}}hf(t_{n+3},y_{n+3})}$
• BDF4: ${\displaystyle y_{n+4}-{\tfrac {48}{25}}y_{n+3}+{\tfrac {36}{25}}y_{n+2}-{\tfrac {16}{25}}y_{n+1}+{\tfrac {3}{25}}y_{n}={\tfrac {12}{25}}hf(t_{n+4},y_{n+4})}$
• BDF5: ${\displaystyle y_{n+5}-{\tfrac {300}{137}}y_{n+4}+{\tfrac {300}{137}}y_{n+3}-{\tfrac {200}{137}}y_{n+2}+{\tfrac {75}{137}}y_{n+1}-{\tfrac {12}{137}}y_{n}={\tfrac {60}{137}}hf(t_{n+5},y_{n+5})}$
• BDF6: ${\displaystyle y_{n+6}-{\tfrac {360}{147}}y_{n+5}+{\tfrac {450}{147}}y_{n+4}-{\tfrac {400}{147}}y_{n+3}+{\tfrac {225}{147}}y_{n+2}-{\tfrac {72}{147}}y_{n+1}+{\tfrac {10}{147}}y_{n}={\tfrac {60}{147}}hf(t_{n+6},y_{n+6})}$

Методы с s > 6 не нулевой стабильный поэтому их нельзя использовать.^[4]

Стабильность

Устойчивость численных методов решения жесткие уравнения обозначается их областью абсолютной стабильности. Для методов BDF эти области показаны на графиках ниже.

В идеале область содержит левую половину комплексной плоскости, и в этом случае метод называется A-устойчивым. Тем не мение, линейные многоступенчатые методы с порядком больше 2 не может быть А-стабильный. Область устойчивости методов BDF более высокого порядка содержит большую часть левой полуплоскости и, в частности, всю отрицательную действительную ось. Методы BDF являются наиболее эффективными линейными многоступенчатыми методами такого рода.^[4]

Розовая область показывает область стабильности методов BDF.

• 

  BDF1

• 

  BDF2

• 

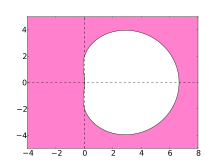
  BDF3

• 

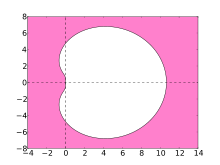
  BDF4

• 

  BDF5

• 

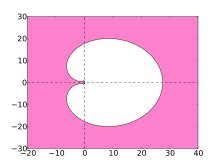
  BDF6

Рекомендации

Цитаты

1. Кертисс, К. Ф., и Хиршфельдер, Дж. О. (1952). Интегрирование жестких уравнений. Слушания Национальной академии наук, 38 (3), 235-243.
2. Ашер и Петцольд 1998, §5.1.2, с. 129
3. Изерлес 1996, п. 27 (для s = 1, 2, 3); Сюли и Майерс 2003, п. 349 (для всех s)
4. Сюли и Майерс 2003, п. 349

Упомянутые работы

• Ascher, U.M .; Петцольд, Л. (1998), Компьютерные методы решения обыкновенных дифференциальных и дифференциально-алгебраических уравнений, СИАМ, Филадельфия, ISBN  0-89871-412-5.
• Изерлес, Арье (1996), Первый курс численного анализа дифференциальных уравнений, Издательство Кембриджского университета, ISBN  978-0-521-55655-2.
• Сули, Эндре; Майерс, Дэвид (2003), Введение в численный анализ, Издательство Кембриджского университета, ISBN  0-521-00794-1.

дальнейшее чтение

• Методы BDF в вики SUNDIALS (SUNDIALS - это библиотека, реализующая методы BDF и подобные алгоритмы).