Эпициклическая передача - Epicyclic gearing

Для кольцевой шестерни, используемой в стартерах, см. Зубчатый венец стартера.

Эта планетарная зубчатая передача состоит из солнечной шестерни (желтая), планетарных шестерен (синяя), поддерживаемых водилом (зеленая) и кольцевой шестерни (розовая). Красные метки показывают относительное смещение солнечной шестерни и водила, когда водило повернуто на 45 ° по часовой стрелке и коронная шестерня остается неподвижной.

An планетарный редуктор (также известный как планетарная передача) состоит из двух шестерни установлен так, чтобы центр одной шестерни вращался вокруг центра другой. Водило соединяет центры двух шестерен и вращается, чтобы нести одну шестерню, называемую планетарная передача или же шестерня планеты, вокруг другой, называется солнечная шестерня или же солнечное колесо. Планетарная и солнечная шестерни входят в зацепление, так что их круги поля катиться без скольжения. Точка на делительной окружности планетарной передачи указывает на эпициклоида изгиб. В этом упрощенном случае солнечная шестерня зафиксирована, а планетарные шестерни вращаются вокруг солнечной шестерни.

Эпициклическая зубчатая передача может быть собрана таким образом, чтобы планетарная шестерня катилась по внутренней части делительной окружности фиксированного внешнего зубчатого колеса или кольцевой шестерни, иногда называемой кольцевая передача. В этом случае кривая, очерченная точкой на делительной окружности планеты, представляет собой гипоциклоида.

Комбинация зубчатых передач эпицикла с планетарной передачей, включающей солнечную шестерню и коронную шестерню, называется планетарная передача.^[1][2] В этом случае коронная шестерня обычно фиксируется, а солнечная шестерня приводится в движение.

Обзор

Эпициклическая передача или же планетарная передача это механизм система, состоящая из одного или нескольких внешних, или планета, шестерни или шестерни, вращаясь вокруг центрального солнечная шестерня или же солнечное колесо.^[3][4] Обычно планетарные шестерни устанавливаются на подвижном рычаге или перевозчик, которая сама может вращаться относительно солнечной шестерни. В планетарных зубчатых передачах также используется внешний звенеть снаряжение или кольцо, который входит в зацепление с планетарными шестернями. Планетарные передачи (или планетарные передачи) обычно классифицируются как простые или составные планетарные передачи. Простые планетарные шестерни имеют одно солнце, одно кольцо, одно водило и один комплект планетарной передачи. Составные планетарные шестерни включают в себя один или несколько из следующих трех типов структур: сетчатая планета (есть по крайней мере еще две планеты, сцепленные друг с другом в каждой цепочке планет), ступенчатая планета (существует соединение валов между двумя планетами в каждый планетарный поезд) и многоступенчатые структуры (система содержит два или более набора планет). По сравнению с простыми планетарными передачами составные планетарные передачи имеют преимущества большего передаточного числа, более высокого отношения крутящего момента к массе и более гибких конфигураций.

Оси всех шестерен обычно параллельны, но для особых случаев, таких как точилки и дифференциалы, их можно разместить под углом, вводя элементы коническая передача (Смотри ниже). Кроме того, солнце, водило планеты и оси кольца обычно коаксиальный.

Книжное колесо, от Агостино Рамелли Разнообразная и искусственная машина, 1588

Также доступна эпициклическая передача, которая состоит из солнца, водила и двух планет, которые сцепляются друг с другом. Одна планета находится в зацеплении с солнечной шестерней, а вторая планета зацепляется с коронной шестерней. В этом случае, когда водило зафиксировано, коронная шестерня вращается в том же направлении, что и солнечная шестерня, обеспечивая реверсирование направления по сравнению со стандартной планетарной передачей.

История

Около 500 г. до н.э. греки изобрели идею эпициклов, кругов, движущихся по круговым орбитам. С этой теорией Клавдий Птолемей в Альмагест в 148 году нашей эры смог предсказать орбитальные траектории планет. В Антикитерский механизм, около 80 г. до н.э., имел зубчатую передачу, которая могла приблизительно соответствовать эллиптическому пути Луны через небеса и даже корректировать девятилетнюю прецессию этого пути.^[5] (Греки видели бы это не как эллиптическое, а как эпициклическое движение.)

В трактате II века нашей эры Альмагест, Птолемей используется вращающийся деферент и эпициклы которые образуют эпициклические зубчатые передачи, чтобы предсказывать движения планет. Точные предсказания движения Солнца, Луны и пяти планет, Меркурия, Венеры, Марса, Юпитера и Сатурна, по небу предполагали, что каждая из них следовала траектории, отслеживаемой точкой на планетарной шестерне планетарной зубчатой ​​передачи. Эта кривая называется эпитрохоид.^{[нужна цитата ]}

Эпициклическая передача использовалась в Антикитерский механизм около 80 г. до н.э., чтобы настроить отображаемое положение луны для эллиптичность его орбиты, и даже для апсидальная прецессия своей орбиты. Две передние шестерни вращались вокруг немного разных центров, и одна приводила в движение другую не с зацеплением зубьев, а со штифтом, вставленным в прорезь на втором. Когда паз приводил в движение вторую передачу, радиус движения изменялся, вызывая ускорение и замедление ведомой шестерни на каждом обороте.^{[нужна цитата ]}

В 11 веке нашей эры планетарная передача была изобретена заново. Ибн Халаф аль-Муради в Аль-Андалус. Его снаряженный водяные часы использовал комплекс зубчатая передача механизм, включающий как сегментную, так и планетарную передачу.^[6][7]

Ричард Уоллингфорд, английский настоятель монастыря Святого Олбана, позже описал планетарную передачу для астрономические часы в 14 веке.^[8] В 1588 г. итальянский военный инженер Агостино Рамелли изобрел книжное колесо, вертикально вращающийся книжный шкаф, содержащий планетарную передачу с двумя уровнями планетарных шестерен для поддержания правильной ориентации книг.^[8][9]

Передаточное отношение стандартной планетарной передачи

В этом примере водило (зеленый) остается неподвижным, а солнечная шестерня (желтая) используется в качестве входного сигнала. Анализ предполагает общий расчетный модуль зубчатой ​​передачи. Планетарные шестерни (синие) вращаются в соотношении, определяемом количеством зубьев каждой шестерни. Здесь соотношение составляет -24/16 или -3/2; каждая планетарная шестерня вращается на 3/2 скорости солнечной шестерни в противоположном направлении.

В передаточное число планетарной зубчатой ​​передачи несколько не интуитивно понятен, особенно потому, что есть несколько способов, которыми входное вращение может быть преобразовано в выходное вращение. Три основных компонента планетарной передачи:

• солнце: Центральная передача
• Перевозчик: Вмещает одно или несколько периферийных Планета шестерни, все одного размера, зацепленные с солнечной шестерней
• Кольцо или кольцевое пространство: Наружное кольцо с обращенными внутрь зубьями, которые входят в зацепление с планетарной шестерней или шестернями.

Общее передаточное число простой планетарной передачи можно рассчитать с помощью следующих двух уравнений:^[1] представляющие взаимодействия солнце-планета и планета-кольцо соответственно:

${\displaystyle {\begin{aligned}{\text{N}}_{\text{s}}\omega _{\text{s}}+{\text{N}}_{\text{p}}\omega _{\text{p}}-({\text{N}}_{\text{s}}+{\text{N}}_{\text{p}})\omega _{\text{c}}&=0\\{\text{N}}_{\text{r}}\omega _{\text{r}}-{\text{N}}_{\text{p}}\omega _{\text{p}}-({\text{N}}_{\text{r}}-{\text{N}}_{\text{p}})\omega _{\text{c}}&=0\end{aligned}}}$

куда

${\displaystyle {\omega _{\text{r}}},{\omega _{\text{s}}},{\omega _{\text{p}}},{\omega _{\text{c}}}}$ это угловая скорость из Звенеть, Солнечная шестерня, Планетарные шестерни и планета носитель соответственно, и

${\displaystyle {{\text{N}}_{\text{r}}},{{\text{N}}_{\text{s}}},{{\text{N}}_{\text{p}}}}$ количество зубьев Звенеть, то Солнечная шестерня и каждый Планетарная передача соответственно.

из чего мы можем получить следующее:

${\displaystyle {\text{N}}_{\text{s}}\omega _{\text{s}}+{\text{N}}_{\text{r}}\omega _{\text{r}}=({\text{N}}_{\text{s}}+{\text{N}}_{\text{r}})\omega _{\text{c}}}$

${\displaystyle \omega _{\text{s}}={\frac {{\text{N}}_{\text{s}}+{\text{N}}_{\text{r}}}{{\text{N}}_{\text{s}}}}\omega _{\text{c}}-{\frac {{\text{N}}_{\text{r}}}{{\text{N}}_{\text{s}}}}\omega _{\text{r}}}$

${\displaystyle \omega _{\text{r}}={\frac {{\text{N}}_{\text{s}}+{\text{N}}_{\text{r}}}{{\text{N}}_{\text{r}}}}\omega _{\text{c}}-{\frac {{\text{N}}_{\text{s}}}{{\text{N}}_{\text{r}}}}\omega _{\text{s}}}$

${\displaystyle \omega _{\text{c}}={\frac {{\text{N}}_{\text{s}}}{{\text{N}}_{\text{s}}+{\text{N}}_{\text{r}}}}\omega _{\text{s}}+{\frac {{\text{N}}_{\text{r}}}{{\text{N}}_{\text{s}}+{\text{N}}_{\text{r}}}}\omega _{\text{r}}}$

и

${\displaystyle -{\frac {{\text{N}}_{\text{r}}}{{\text{N}}_{\text{s}}}}={\frac {\omega _{\text{s}}-\omega _{\text{c}}}{\omega _{\text{r}}-\omega _{\text{c}}}}}$

Учитывая ${\displaystyle \omega _{\text{r}}\neq \omega _{\text{c}}}$.^[10]

В качестве альтернативы, если количество зубьев каждой шестерни соответствует соотношению ${\displaystyle N_{\text{r}}=N_{\text{s}}+2N_{\text{p}}}$, это уравнение можно переписать в следующем виде:

${\displaystyle n\omega _{\text{s}}+(2+n)\omega _{\text{r}}-2(1+n)\omega _{\text{c}}=0}$

куда

${\displaystyle n=N_{\text{s}}/N_{\text{p}}}$

Эти отношения могут быть использованы для анализа любой эпициклической системы, включая такие, как трансмиссии гибридных транспортных средств, где два компонента используются как входы с третьим предоставлением выход относительно двух входов.^[11]

Во многих планетарных зубчатых передачах один из этих трех основных компонентов остается неподвижным; один из двух оставшихся компонентов - Вход, обеспечивая питание системы, а последний компонент - выход, получая питание от системы. Отношение входного вращения к выходному вращению зависит от количества зубьев в каждой шестерне и от того, какой компонент удерживается в неподвижном состоянии.

В одном варианте водило планетарной передачи (зеленое) удерживается в неподвижном состоянии, а солнечная шестерня (желтая) используется в качестве входной. В этом случае планетарные шестерни просто вращаются вокруг своих осей (т. Е. Вращаются) со скоростью, определяемой количеством зубьев каждой шестерни. Если солнечная шестерня Ns зубьев, и каждая планетарная шестерня имеет Np зубьев, то соотношение равно -N_s/N_п. Например, если солнечная шестерня имеет 24 зуба, а каждая планетарная передача имеет 16 зубцов, то передаточное число равно −24/16 или −3/2; это означает, что один по часовой стрелке оборот солнечной шестерни дает 1,5 против часовой стрелки повороты каждой планетарной шестерни вокруг своей оси.

Это вращение планетарных шестерен, в свою очередь, может приводить в движение коронную шестерню (не изображенную на схеме) в соответствующем передаточном числе. Если коронная шестерня имеет N_р зубьев, то кольцо будет вращаться на N_п/N_р оборотов за каждый оборот планетарной передачи. Например, если коронная шестерня имеет 64 зубца, а планетарные шестерни - 16, один оборот планетарной шестерни по часовой стрелке приводит к 16/64 или 1/4 оборота по часовой стрелке кольцевой шестерни. Расширение этого случая от случая выше:

• Один оборот солнечной шестерни приводит к ${\displaystyle -N_{\text{s}}/N_{\text{p}}}$ повороты планет
• Один оборот планетарной передачи приводит к ${\displaystyle N_{\text{p}}/N_{\text{r}}}$ обороты зубчатого венца

Таким образом, при заблокированном водиле планетарной передачи один оборот солнечной шестерни приводит к ${\displaystyle -N_{\text{s}}/N_{\text{r}}}$ обороты коронной шестерни.

Кольцевая шестерня также может удерживаться неподвижной, с входом в водило планетарной шестерни; выходное вращение затем производится солнечной шестерней. Эта конфигурация приведет к увеличению передаточного числа, равному 1+.N_р/N_s.^{[нужна цитата ]}

Если коронная шестерня удерживается неподвижно, а солнечная шестерня используется в качестве входной, водило планетарной передачи будет выходным. Передаточное число в этом случае будет 1 / (1 +N_р/N_s), который также можно записать как 1: (1 +N_р/N_s). Это самое низкое передаточное число, достижимое с планетарной зубчатой ​​передачей. Этот тип зубчатой ​​передачи иногда используется в тракторы и строительное оборудование для обеспечения высокого крутящего момента на ведущие колеса.

На велосипеде ступичные шестерни Солнце обычно неподвижно, привязано к оси или даже обработано прямо на ней. Водило планетарной передачи используется в качестве входного. В этом случае передаточное число просто определяется как (N_s+N_р)/N_р. Количество зубьев планетарной шестерни значения не имеет.

Составные планеты Sturmey-Archer Ступица велосипеда AM (зубчатый венец снят)

Ускорения стандартной планетарной передачи

Из приведенных выше формул мы также можем получить ускорения солнца, кольца и носителя, которые равны:

${\displaystyle \alpha _{\text{s}}={\frac {{\text{N}}_{\text{s}}+{\text{N}}_{\text{r}}}{{\text{N}}_{\text{s}}}}\alpha _{\text{c}}-{\frac {{\text{N}}_{\text{r}}}{{\text{N}}_{\text{s}}}}\alpha _{\text{r}}}$

${\displaystyle \alpha _{\text{r}}={\frac {{\text{N}}_{\text{s}}+{\text{N}}_{\text{r}}}{{\text{N}}_{\text{r}}}}\alpha _{\text{c}}-{\frac {{\text{N}}_{\text{s}}}{{\text{N}}_{\text{r}}}}\alpha _{\text{s}}}$

${\displaystyle \alpha _{\text{c}}={\frac {{\text{N}}_{\text{s}}}{{\text{N}}_{\text{s}}+{\text{N}}_{\text{r}}}}\alpha _{\text{s}}+{\frac {{\text{N}}_{\text{r}}}{{\text{N}}_{\text{s}}+{\text{N}}_{\text{r}}}}\alpha _{\text{r}}}$

Передаточные числа стандартной планетарной передачи

В планетарных передачах необходимо знать две скорости, чтобы определить третью скорость. Однако в установившемся режиме должен быть известен только один крутящий момент, чтобы определить два других крутящих момента. Уравнения, определяющие крутящий момент:

${\displaystyle \tau _{r}=\tau _{s}{\frac {N_{r}}{N_{s}}}}$

${\displaystyle \tau _{r}=-\tau _{c}{\frac {N_{r}}{N_{r}+N_{s}}}}$

${\displaystyle \tau _{c}=-\tau _{r}{\frac {N_{r}+N_{s}}{N_{r}}}}$

${\displaystyle \tau _{c}=-\tau _{s}{\frac {N_{r}+N_{s}}{N_{s}}}}$

${\displaystyle \tau _{s}=\tau _{r}{\frac {N_{s}}{N_{r}}}}$

${\displaystyle \tau _{s}=-\tau _{c}{\frac {N_{s}}{N_{r}+N_{s}}}}$

куда: ${\displaystyle \tau _{r}}$ - крутящий момент кольца (затрубного пространства), ${\displaystyle \tau _{s}}$ - крутящий момент солнца, ${\displaystyle \tau _{c}}$- Крутящий момент несущей. Для всех трех это крутящие моменты, прилагаемые к механизму (входные крутящие моменты). Выходные крутящие моменты имеют обратный знак входным крутящим моментам.

В случаях, когда шестерни ускоряются или для учета трения, эти уравнения необходимо изменить.

Коэффициент фиксированного состава перевозчика

Удобный подход к определению различных передаточных чисел, доступных в планетарной зубчатой ​​передаче, начинается с рассмотрения передаточного числа зубчатой ​​передачи, когда водило удерживается неподвижным. Это известно как фиксированное передаточное число несущей.^[2]

В случае простой планетарной зубчатой ​​передачи, образованной водилом, поддерживающим планетарную шестерню, зацепленную с солнечной и коронной шестернями, фиксированное передаточное число водила вычисляется как передаточное число зубчатая передача образуется солнечной, планетарной и коронной шестернями на неподвижном водиле. Это дается

${\displaystyle R={\frac {\omega _{s}}{\omega _{r}}}=-{\frac {N_{r}}{N_{s}}}.}$

В этом расчете планетарная шестерня является промежуточной шестерней.

Основная формула планетарной зубчатой ​​передачи с вращающимся водилом получается из признания того, что эта формула остается верной, если угловые скорости солнца, планетарной передачи и зубчатого венца вычисляются относительно угловой скорости водила. Это становится,

${\displaystyle R={\frac {\omega _{s}-\omega _{c}}{\omega _{r}-\omega _{c}}}.}$

Эта формула обеспечивает простой способ определения передаточных чисел простой планетарной зубчатой ​​передачи в различных условиях:

1. Держатель удерживается неподвижным, ω_c=0,

${\displaystyle {\frac {\omega _{s}}{\omega _{r}}}=R,\quad {\mbox{so}}\quad {\frac {\omega _{s}}{\omega _{r}}}=-{\frac {N_{r}}{N_{s}}}.}$

2. Зубчатый венец удерживается неподвижным, ω_р=0,

${\displaystyle {\frac {\omega _{s}-\omega _{c}}{-\omega _{c}}}=R,\quad {\mbox{or}}\quad {\frac {\omega _{s}}{\omega _{c}}}=1-R,\quad {\mbox{so}}\quad {\frac {\omega _{s}}{\omega _{c}}}=1+{\frac {N_{r}}{N_{s}}}.}$

3. Солнечная шестерня удерживается неподвижно, ω_s=0,

${\displaystyle {\frac {-\omega _{c}}{\omega _{r}-\omega _{c}}}=R,\quad {\mbox{or}}\quad {\frac {\omega _{r}}{\omega _{c}}}=1-{\frac {1}{R}},\quad {\mbox{so}}\quad {\frac {\omega _{r}}{\omega _{c}}}=1+{\frac {N_{s}}{N_{r}}}.}$

Каждое из передаточных чисел, доступных для простой планетарной зубчатой ​​передачи, может быть получено с помощью ленточных тормозов для удержания и освобождения водила, солнечной или кольцевой шестерни по мере необходимости. Это обеспечивает базовую структуру для автоматическая коробка передач.

Дифференциал цилиндрической шестерни

Дифференциал с цилиндрической зубчатой ​​передачей, созданный путем зацепления планетарных шестерен двух соосных планетарных зубчатых передач. Кожух является водилом планетарной зубчатой ​​передачи.

А прямозубый дифференциал состоит из двух идентичных коаксиальных планетарных зубчатых передач, собранных с одним водилом, так что их планетарные шестерни входят в зацепление. Это формирует планетарную зубчатую передачу с фиксированным передаточным числом несущей р = −1.

В этом случае основная формула планетарной зубчатой ​​передачи дает

${\displaystyle {\frac {\omega _{s}-\omega _{c}}{\omega _{r}-\omega _{c}}}=-1,}$

или же

${\displaystyle \omega _{c}={\frac {1}{2}}(\omega _{s}+\omega _{r}).}$

Таким образом, угловая скорость водила дифференциала прямозубой шестерни представляет собой среднее значение угловых скоростей солнечной и коронной шестерен.

При обсуждении дифференциала прямозубой шестерни употребление термина кольцевая шестерня - это удобный способ отличить солнечные шестерни двух планетарных зубчатых передач. Вторая солнечная шестерня служит той же цели, что и коронная шестерня простой планетарной зубчатой ​​передачи, но явно не имеет внутреннего зубчатого сопряжения, типичного для кольцевой шестерни.^[1]

Передаточное число реверсивной планетарной передачи

CSS-анимации планетарной передачи с заблокированной коронной шестерней на 56 зубьев (1), солнечной шестерней на 24 зуба заблокированной (2), водило с заблокированной шестерней планетарной передачи на 16 зубьев (3) и прямым приводом (4) - числа обозначают относительную угловую скорость

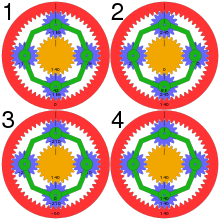
В некоторых планетарных зубчатых передачах используются две планетарные шестерни, которые зацепляются друг с другом. Одна из этих планет находится в зацеплении с солнечной шестерней, другая - с коронной шестерней. Это приводит к тому, что планетарная система генерирует разные соотношения. Основное уравнение становится:

${\displaystyle (R-1)\omega _{\text{c}}=R\omega _{\text{r}}-\omega _{\text{s}}}$

куда ${\displaystyle R=N_{\text{r}}/N_{\text{s}}}$

что приводит к:

${\displaystyle \omega _{\text{r}}=\omega _{\text{s}}(1/R)}$ когда носитель заблокирован,

${\displaystyle \omega _{\text{r}}=\omega _{\text{c}}(R-1)/R}$ когда солнце закрыто,

${\displaystyle \omega _{\text{s}}=-\omega _{\text{c}}(R-1)}$ когда зубчатый венец заблокирован.

Составные планетарные передачи

Ступенчатая планета серии Rohloff Speedhub ступица велосипеда с внутренним редуктором при этом меньшая серия планет зацепляется с солнечным колесом, а большая серия планет зацепляется с коронной шестерней

«Составная планетарная передача» - это общее понятие, и оно относится к любым планетарным передачам, включающим один или несколько из следующих трех типов структур: сетчатая планета (в каждой цепочке планет есть не менее двух или более планет, сцепленных друг с другом), ступенчатая планета (существует соединение вала между двумя планетами в каждом планетном поезде), и многоступенчатые конструкции (система содержит два и более набора планет).

В некоторых конструкциях используется «ступенчатая планета», в которой на обоих концах общего вала установлены две шестерни разного размера. Малый конец касается солнца, а большой конец - зубчатого венца. Это может быть необходимо для достижения меньших ступенчатых изменений передаточного числа, когда общий размер упаковки ограничен. Составные планеты имеют «временные метки» (или, в техническом выражении, «относительную фазу зубчатого зацепления»). Условия сборки составных планетарных шестерен более жесткие, чем простых планетарных передач,^[12] и они должны быть собраны в правильной начальной ориентации относительно друг друга, иначе их зубья не будут одновременно взаимодействовать с солнцем и коронной шестерней на противоположных концах планетарной передачи, что приведет к очень плохой работе и короткому сроку службы. Составные планетарные шестерни могут легко достичь большего передаточного числа при равном или меньшем объеме. Например, составные планеты с зубьями в соотношении 2: 1 с коронной шестерней 50 зубьев дадут тот же эффект, что и коронная шестерня 100 зубьев, но с половиной фактического диаметра.

Дополнительные планетарные и солнечные редукторы могут быть последовательно размещены в одном корпусе (где выходной вал первой ступени становится входным валом следующей ступени), обеспечивая большее (или меньшее) передаточное число. Это самый способ автоматические трансмиссии работай. В некоторых случаях несколько ступеней могут даже использовать одну и ту же коронную шестерню, которая может быть удлинена по длине трансмиссии или даже быть структурной частью корпуса меньших коробок передач.

В течение Вторая Мировая Война, была разработана специальная разновидность планетарной передачи для переносных радар передача, где требовалось очень высокое передаточное число в небольшом корпусе. У него было две шестерни с наружным кольцом, каждая из которых была вдвое меньше остальных шестерен. Одно из этих двух зубчатых венцов было неподвижным и имело на один зуб меньше, чем на другое. Таким образом, несколько оборотов «солнечной» шестерни заставляли «планетарные» шестерни совершить один оборот, что, в свою очередь, заставляло вращающуюся коронную шестерню вращаться на один зуб, как Циклоидальный привод.^{[нужна цитата ]}

Преимущества

Механизм точилка со стационарной коронной шестерней и вращающимся водилом планетарной передачи на входе. Планетарные передачи превращены в цилиндрические фрезы, вращающиеся вокруг карандаша, расположенного на солнечной оси. Оси планетарных шестерен стыкуются под углом заточки карандаша.

Планетарные зубчатые передачи обеспечивают высокую удельную мощность по сравнению со стандартными зубчатыми передачами с параллельными осями. Они обеспечивают уменьшение объема, несколько кинематических комбинаций, чисто крутильные реакции и соосный вал. К недостаткам можно отнести высокие нагрузки на подшипники, постоянные требования к смазке, недоступность и сложность конструкции.^[13][14]

Потеря эффективности планетарной зубчатой ​​передачи обычно составляет около 3% на ступень.^[15] Такой КПД гарантирует, что большая часть (около 97%) потребляемой энергии передается через коробку передач, а не тратится на механические потери внутри коробки передач.

Нагрузка в планетарной зубчатой ​​передаче распределяется между несколькими планетами; следовательно, крутящий момент значительно увеличивается. Чем больше планет в системе, тем больше грузоподъемность и выше плотность крутящего момента.

Планетарный редуктор также обеспечивает стабильность за счет равномерного распределения массы и повышенной жесткости вращения. Крутящий момент, приложенный радиально к шестерням планетарной зубчатой ​​передачи, передается через шестерню радиально без бокового давления на зубья шестерни.

Обычно мощность привода передается на солнечную шестерню. Затем солнечная шестерня приводит в движение планетарные шестерни, собранные с внешним зубчатым венцом. Вся система планетарной передачи вращается вокруг своей оси и вдоль внешнего зубчатого колеса, где выходной вал, соединенный с водилом планетарной передачи, достигает цели снижения скорости. Более высокое передаточное отношение может быть достигнуто за счет удвоения многоступенчатых шестерен и планетарных шестерен, которые могут работать с одним и тем же венцом.

Метод движения конструкции планетарной передачи отличается от традиционных параллельных передач. Традиционные шестерни полагаются на небольшое количество точек контакта между двумя шестернями для передачи движущей силы. В этом случае вся нагрузка сосредоточена на нескольких контактирующих поверхностях, в результате чего шестерни быстро изнашиваются и иногда трескаются. Но планетарный редуктор имеет несколько поверхностей контакта шестерен с большей площадью, что позволяет равномерно распределять нагрузку вокруг центральной оси. Несколько поверхностей шестерни равномерно распределяют нагрузку, включая любую мгновенную ударную нагрузку, что делает их более устойчивыми к повреждениям от более высокого крутящего момента. Корпус и детали подшипника также с меньшей вероятностью будут повреждены из-за высоких нагрузок, поскольку только подшипники водила планетарной передачи испытывают значительную поперечную силу от передачи крутящего момента, радиальные силы противостоят друг другу и уравновешены, а осевые силы возникают только при использовании косозубых шестерен.

3D печать

Анимация печатной шестеренки

Планетарные передачи стали популярными в 3D печать по нескольким разным причинам. Планетарные коробки передач могут обеспечить большое передаточное число в небольшом и легком корпусе. Некоторые люди устанавливают такие редукторы, чтобы получать более точные 3D-отпечатки, уменьшая движение своих шаговых двигателей.

Мотор с редуктором должен вращаться все дальше и быстрее, чтобы обеспечить такое же выходное движение в 3D-принтере, что является преимуществом, если его не перевешивает более низкая скорость движения. Если шаговый двигатель должен вращаться дальше, он также должен сделать больше шагов, чтобы переместить принтер на заданное расстояние; Таким образом, шаговый двигатель с пониженной передачей имеет меньший минимальный размер шага, чем тот же шаговый двигатель без коробки передач. Несмотря на множество факторов, планетарные редукторы могут помочь в создании 3D-печати очень высокого качества.

Одно из популярных применений планетарных систем, напечатанных на 3D-принтере, - это игрушки для детей.^{[нужна цитата ]} С шестерни в елочку легко распечатать на 3D-принтере, стало очень популярно печатать на 3D-принтере подвижную планетарную зубчатую передачу в виде елочки для обучения детей принципам работы шестерен. Преимущество шестерен типа «елочка» в том, что они не выпадают из кольца и не требуют монтажной пластины, что позволяет четко видеть движущиеся части.

Галерея

• 

  Разъемное кольцо, составная планетарная передача, планетарные шестерни позиционера автомобильного зеркала заднего вида. Передаточное отношение входной солнечной шестерни к выходной черной коронной шестерне составляет −5/352.

• 
• 

  Редукторы включены Пратт энд Уитни Канада PT6 газотурбинный двигатель.

• 

  Один из трех наборов из трех шестерен внутри водила планетарной передачи Ford FMX. Равиньо коробка передач

Смотрите также

• Гипоциклоидная передача
• Антикитерский механизм - древний механический астрономический компьютер
• Бесступенчатая коробка передач (Вариатор)
• Циклоидальный привод
• Эпициклоида
• Ford Модель T - имел двухступенчатую планетарную трансмиссию.
• Коробка передач
• Гармонический драйв
• Ступица, для велосипедов и др.
• Бесступенчатая трансмиссия NuVinci
• Планетарный редуктор Ravigneaux
• Rohloff Speedhub - 14-ступенчатая коробка передач ступицы велосипеда
• Планетарный редуктор Simpson
• Стурми Лучник - Первый крупный производитель велосипедных ступиц с планетарной передачей

Рекомендации

1. Дж. Дж. Уикер, Г. Р. Пеннок и Дж. Э. Шигли, 2003 г., Теория машин и механизмов, Издательство Оксфордского университета, Нью-Йорк.
2. Б. Пол, 1979 г., Кинематика и динамика плоских машин., Прентис Холл.
3. Хиллер, V.A.W. (2001). «Планетарный редуктор и однонаправленные муфты». Основы автомобильной техники (4-е изд.). Челтнем, Великобритания: Нельсон Торнс. п. 244. ISBN  0-74-870531-7.
4. Harrison, H .; Нетлтон, Т. (1994). Принципы инженерной механики (2-е изд.). Оксфорд, Великобритания: Баттерворт-Хайнеманн. п. 58. ISBN  0-34-056831-3.
5. Райт, М. Т. (2007). «Пересмотр антикиферского механизма» (PDF). Междисциплинарные научные обзоры. 32 (1): 27–43. Дои:10.1179 / 030801807X163670. Получено 20 мая 2014.
6. Хасан, Ахмад Ю., Передача исламских технологий на Запад, Часть II: Передача исламской инженерии, История науки и техники в исламе
7. Дональд Рутледж Хилл (1996). История инженерной мысли в классические и средневековые времена. Рутледж. С. 203, 223, 242. ISBN  0-415-15291-7.
8. Дж. Дж. Кой, Д. П. Таунсенд, Е. В. Зарецкий, "Gearing", справочная публикация НАСА 1152, технический отчет AVSCOM 84-C-15, 1985
9. Чад Рэндл, "Вращающаяся архитектура: история зданий, которые вращаются, поворачиваются и поворачиваются", стр. 19.
10. «Как вывести и рассчитать уравнения планетарного передаточного числа планетарных зубчатых передач».
11. Джон М. Миллер (май 2006 г.). «Архитектура силовой установки гибридного электромобиля типа e-CVT». IEEE Transactions по силовой электронике. 21 (3): 756–767. Bibcode:2006ITPE ... 21..756M. Дои:10.1109 / TPEL.2006.872372.
12. П. А. Симионеску (1 сентября 1998 г.). «Единый подход к состоянию сборки планетарных шестерен». Журнал механического проектирования. 120 (3): 448–453. Дои:10.1115/1.2829172.
13. Линвандер, П., 1983 г., Системы зубчатого привода: конструкция и применение. Марсель Деккер, Нью-Йорк
14. Смит, Дж. Д., 1983, Шестерни и их вибрация: основной подход к пониманию шума шестерен. Марсель Деккер, Нью-Йорк и Макмиллан, Лондон
15. «Планетарная передача» (PDF). people.eecs.berkeley.edu. 2011. Получено 2019-09-29.

внешняя ссылка

• Кинематические модели для цифровой библиотеки дизайна (KMODDL), фильмы и фотографии сотен работающих моделей механических систем в Корнелле.
• «Анимация планетарной передачи в SVG»
• «Анимация планетарной передачи»
• "Устройство разделения мощности"
• "Интерактивное руководство по планетарной передаче"
• Коробка передач Prius
• Планетарный редуктор
• Кандидат наук. Диссертация о сложных планетарных передачах
• Краткие рекомендации по анализу планетарной передачи
• Веториальная аннимация: кольцо, планеты и солнечная шестерня.