Коэффициенты Эйнштейна - Einstein coefficients

Линии излучения и линии поглощения по сравнению с непрерывным спектром

Коэффициенты Эйнштейна являются математическими величинами, которые являются мерой вероятности поглощения или излучения света атомом или молекулой.^[1] Эйнштейн А коэффициенты связаны со скоростью спонтанное излучение света, и Эйнштейн B коэффициенты связаны с поглощение и стимулированное излучение света.

Спектральные линии

В физика, можно представить себе спектральную линию с двух точек зрения.

Линия излучения образуется, когда атом или молекула совершают переход из определенного дискретного уровень энергии E₂ атома на более низкий энергетический уровень E₁, излучающий фотон определенной энергии и длины волны. Спектр многих таких фотонов покажет выброс излучения на длине волны, связанной с этими фотонами.

Линия поглощения образуется при переходе атома или молекулы из нижнего E₁, в более высокое дискретное энергетическое состояние, E₂, при этом фотон поглощается. Эти поглощенные фотоны обычно происходят из фонового континуального излучения (полный спектр электромагнитного излучения), и спектр будет показывать спад непрерывного излучения на длине волны, связанной с поглощенными фотонами.

Два государства должны быть связанные состояния в котором электрон связан с атомом или молекулой, поэтому переход иногда называют переходом «связанный-связанный», в отличие от перехода, при котором электрон полностью выбрасывается из атома («связанный-свободный» переход) в континуум состояние, оставив ионизированный атома и генерирует непрерывное излучение.

А фотон с энергией, равной разности E₂ − E₁ между уровнями энергии высвобождается или поглощается в процессе. Частота ν на которой возникает спектральная линия, связана с энергией фотона соотношением Частотное условие Бора E₂ − E₁ = hν куда час обозначает Постоянная Планка.^{[2][3][4][5][6][7]}

Коэффициенты эмиссии и поглощения

Атомная спектральная линия относится к событиям излучения и поглощения в газе, в котором ${\displaystyle n_{2}}$ - плотность атомов в верхнем энергетическом состоянии линии, а ${\displaystyle n_{1}}$ - плотность атомов в низкоэнергетическом состоянии линии.

Излучение атомной линии излучения с частотой ν может быть описан коэффициент выбросов ${\displaystyle \epsilon }$ в единицах энергии / (время × объем × телесный угол). ε dt dV dΩ тогда энергия, излучаемая элементом объема ${\displaystyle dV}$ во время ${\displaystyle dt}$ в телесный угол ${\displaystyle d\Omega }$. Для атомного линейного излучения

${\displaystyle \epsilon ={\frac {h\nu }{4\pi }}n_{2}A_{21},}$

куда ${\displaystyle A_{21}}$ - коэффициент Эйнштейна для спонтанного излучения, который фиксируется внутренними свойствами соответствующего атома для двух соответствующих уровней энергии.

Поглощение излучения атомных линий можно описать коэффициент поглощения ${\displaystyle \kappa }$ с единицами измерения 1 / длины. Выражение κ 'dx дает долю интенсивности, поглощаемую световым лучом на частоте ν во время путешествия расстояние dx. Коэффициент поглощения определяется выражением

${\displaystyle \kappa '={\frac {h\nu }{4\pi }}(n_{1}B_{12}-n_{2}B_{21}),}$

куда ${\displaystyle B_{12}}$ и ${\displaystyle B_{21}}$ - коэффициенты Эйнштейна для поглощения фотонов и индуцированного излучения соответственно. Как коэффициент ${\displaystyle A_{21}}$, они также фиксируются внутренними свойствами соответствующего атома для двух соответствующих уровней энергии. Для термодинамики и для применения Закон Кирхгофа, необходимо, чтобы полное поглощение выражалось как алгебраическая сумма двух компонент, описываемых соответственно формулой ${\displaystyle B_{12}}$ и ${\displaystyle B_{21}}$, которые можно рассматривать как положительное и отрицательное поглощение, которые представляют собой, соответственно, прямое поглощение фотонов и то, что обычно называют стимулированным или индуцированным излучением.^[8][9][10]

В приведенных выше уравнениях не учитывается влияние спектроскопическая форма линии. Чтобы быть точным, приведенные выше уравнения необходимо умножить на (нормализованную) форму спектральной линии, и в этом случае единицы измерения изменятся, чтобы включить член 1 / Гц.

В условиях термодинамического равновесия числовые плотности ${\displaystyle n_{2}}$ и ${\displaystyle n_{1}}$, коэффициенты Эйнштейна и спектральная плотность энергии предоставляют достаточную информацию для определения скорости поглощения и излучения.

Условия равновесия

Числовые плотности ${\displaystyle n_{2}}$ спектр и ${\displaystyle n_{1}}$ задаются физическим состоянием газа, в котором находится спектральная линия, включая локальную спектральное сияние (или, в некоторых презентациях, локальная спектральная плотность лучистой энергии). Когда это состояние является одним из строгих термодинамическое равновесие, или одно из так называемых «локальных термодинамических равновесий»,^[11][12][13] тогда распределение состояний возбуждения атомов (которое включает ${\displaystyle n_{2}}$ и ${\displaystyle n_{1}}$) определяет скорости атомных выбросов и абсорбций так, чтобы Закон Кирхгофа о равенстве радиационной поглощающей способности и излучательной способности держит. В строгом термодинамическом равновесии поле излучения называется излучение черного тела и описывается Закон планка. Для локального термодинамического равновесия поле излучения не обязательно должно быть полем черного тела, но скорость межатомных столкновений должна значительно превышать скорости поглощения и испускания квантов света, так что межатомные столкновения полностью доминируют в распределении состояний возбуждения атомов. Возникают обстоятельства, при которых локальное термодинамическое равновесие не преобладает, потому что сильные радиационные эффекты подавляют тенденцию к Распределение Максвелла – Больцмана молекулярных скоростей. Например, в атмосфере Солнца преобладает большая сила излучения. В верхних слоях атмосферы Земли, на высотах более 100 км, решающее значение имеет редкость межмолекулярных столкновений.

В случаях термодинамическое равновесие и из локальное термодинамическое равновесие плотность атомов, как возбужденных, так и невозбужденных, может быть вычислена из Распределение Максвелла – Больцмана, но для других случаев (например, лазеры ) расчет сложнее.

Коэффициенты Эйнштейна

В 1916 г. Альберт Эйнштейн предположил, что при образовании атомной спектральной линии происходят три процесса. Эти три процесса называются спонтанным излучением, вынужденным излучением и поглощением. С каждым связан коэффициент Эйнштейна, который является мерой вероятности того, что этот конкретный процесс произойдет. Эйнштейн рассмотрел случай изотропного излучения с частотой ν и спектральная плотность энергии ρ(ν).^{[3][14][15][16]}

Различные составы

Хилборн сравнил различные формулировки вывода коэффициентов Эйнштейна разными авторами.^[17] Например, Герцберг работает с освещенностью и волновым числом;^[18] Ярив работает с энергией на единицу объема на единицу частотного интервала,^[19] как и в более позднем (2008 г.) ^[20] формулировка. Михалас и Вайбель-Михалас работают с сиянием и частотой;^[13] также Чандрасекар;^[21] также Гуди и Юнг;^[22] Loudon использует угловую частоту и яркость.^[23]

Спонтанное излучение

Основная статья: Спонтанное излучение

Принципиальная схема спонтанного излучения атомов

Спонтанное излучение - это процесс, при котором электрон «спонтанно» (то есть без какого-либо внешнего воздействия) распадается с более высокого энергетического уровня на более низкий. Процесс описывается коэффициентом Эйнштейна А₂₁ (s⁻¹), что дает вероятность в единицу времени, что электрон в состоянии 2 с энергией ${\displaystyle E_{2}}$ спонтанно распадется до состояния 1 с энергией ${\displaystyle E_{1}}$, испуская фотон с энергией E₂ − E₁ = hν. Из-за принцип неопределенности энергии-времени, переход фактически производит фотоны в узком диапазоне частот, называемом спектральная ширина линии. Если ${\displaystyle n_{i}}$ плотность атомов в состоянии я , то изменение плотности атомов в состоянии 2 в единицу времени из-за спонтанного излучения будет

${\displaystyle \left({\frac {dn_{2}}{dt}}\right)_{\text{spontaneous}}=-A_{21}n_{2}.}$

Тот же процесс приводит к увеличению населения государства 1:

${\displaystyle \left({\frac {dn_{1}}{dt}}\right)_{\text{spontaneous}}=A_{21}n_{2}.}$

Вынужденное излучение

Основная статья: Вынужденное излучение

Принципиальная схема атомно-стимулированного излучения

Вынужденное излучение (также известный как индуцированная эмиссия) - это процесс, при котором электрон вынужден перейти с более высокого уровня энергии на более низкий из-за присутствия электромагнитного излучения на частоте перехода (или около нее). С термодинамической точки зрения этот процесс следует рассматривать как отрицательное поглощение. Процесс описывается коэффициентом Эйнштейна ${\displaystyle B_{21}}$ (м³ J⁻¹ s⁻²), что дает вероятность в единицу времени на единицу спектральной яркости поля излучения, что электрон в состоянии 2 с энергией ${\displaystyle E_{2}}$ распадется до состояния 1 с энергией ${\displaystyle E_{1}}$, испуская фотон с энергией E₂ − E₁ = hν. Изменение плотности атомов в состоянии 1 в единицу времени из-за индуцированной эмиссии будет

${\displaystyle \left({\frac {dn_{1}}{dt}}\right)_{\text{neg. absorb.}}=B_{21}n_{2}\rho (\nu ),}$

куда ${\displaystyle \rho (\nu )}$ обозначает яркость в полосе пропускания 1 Гц поля изотропного излучения на частоте перехода (см. Закон планка ).

Вынужденная эмиссия - один из фундаментальных процессов, которые привели к развитию лазер. Однако лазерное излучение очень далеко от настоящего случая изотропного излучения.

Поглощение фотонов

Основная статья: Поглощение (оптика)

Принципиальная схема атомной абсорбции

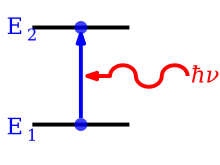
Поглощение - это процесс, при котором фотон поглощается атомом, заставляя электрон перепрыгивать с более низкого энергетического уровня на более высокий. Процесс описывается коэффициентом Эйнштейна ${\displaystyle B_{12}}$ (м³ J⁻¹ s⁻²), что дает вероятность в единицу времени на единицу спектральной яркости поля излучения, что электрон в состоянии 1 с энергией ${\displaystyle E_{1}}$ поглотит фотон с энергией E₂ − E₁ = hν и перейти в состояние 2 с энергией ${\displaystyle E_{2}}$. Изменение плотности атомов в состоянии 1 в единицу времени из-за поглощения будет

${\displaystyle \left({\frac {dn_{1}}{dt}}\right)_{\text{pos. absorb.}}=-B_{12}n_{1}\rho (\nu ).}$

Детальная балансировка

Коэффициенты Эйнштейна представляют собой фиксированные вероятности на время, связанные с каждым атомом, и не зависят от состояния газа, частью которого являются атомы. Следовательно, любое соотношение, которое мы можем вывести между коэффициентами, скажем, при термодинамическом равновесии, будет иметь универсальное значение.

В термодинамическом равновесии у нас будет простая балансировка, при которой чистое изменение числа любых возбужденных атомов равно нулю, уравновешиваясь потерями и прибылью из-за всех процессов. Что касается переходов с ограниченной границей, мы будем иметь детальная балансировка также, в котором говорится, что чистый обмен между любыми двумя уровнями будет сбалансированным. Это связано с тем, что на вероятность перехода не может повлиять присутствие или отсутствие других возбужденных атомов. Детальный баланс (действительный только в состоянии равновесия) требует, чтобы изменение во времени количества атомов на уровне 1 из-за вышеупомянутых трех процессов было равно нулю:

${\displaystyle 0=A_{21}n_{2}+B_{21}n_{2}\rho (\nu )-B_{12}n_{1}\rho (\nu ).}$

Наряду с детальной балансировкой при температуре Т мы можем использовать наши знания о равновесном распределении энергии атомов, как указано в Распределение Максвелла – Больцмана, и равновесное распределение фотонов, как указано в Закон планка излучения черного тела вывести универсальные соотношения между коэффициентами Эйнштейна.

Из распределения Больцмана для числа возбужденных видов атомов имеем я:

${\displaystyle {\frac {n_{i}}{n}}={\frac {g_{i}e^{-E_{i}/kT}}{Z}},}$

куда п это полная плотность атомов, возбужденных и невозбужденных, k является Постоянная Больцмана, Т это температура, ${\displaystyle g_{i}}$ - вырождение (также называемое кратностью) состояния я, и Z это функция распределения. Из закона Планка о излучении черного тела при температуре Т у нас есть спектральная яркость (яркость - это энергия в единицу времени на единицу телесного угла на единицу проецируемой площади при интегрировании по соответствующему спектральному интервалу)^[24] с частотой ν

${\displaystyle \rho _{\nu }(\nu ,T)=F(\nu ){\frac {1}{e^{h\nu /kT}-1}},}$

куда^[25]

${\displaystyle F(\nu )={\frac {2h\nu ^{3}}{c^{3}}},}$

куда ${\displaystyle c}$ это скорость света и ${\displaystyle h}$ является Постоянная Планка.

Подставляя эти выражения в уравнение детальной балансировки и запоминая, что E₂ − E₁ = hν дает

${\displaystyle A_{21}g_{2}e^{-h\nu /kT}+B_{21}g_{2}e^{-h\nu /kT}{\frac {F(\nu )}{e^{h\nu /kT}-1}}=B_{12}g_{1}{\frac {F(\nu )}{e^{h\nu /kT}-1}},}$

разделение на

${\displaystyle A_{21}g_{2}(e^{h\nu /kT}-1)+B_{21}g_{2}F(\nu )=B_{12}g_{1}e^{h\nu /kT}F(\nu ).}$

Приведенное выше уравнение должно выполняться при любой температуре, поэтому

${\displaystyle B_{21}g_{2}=B_{12}g_{1},}$

и

${\displaystyle -A_{21}g_{2}+B_{21}g_{2}F(\nu )=0.}$

Следовательно, три коэффициента Эйнштейна связаны между собой соотношением

${\displaystyle {\frac {A_{21}}{B_{21}}}=F(\nu )}$

и

${\displaystyle {\frac {B_{21}}{B_{12}}}={\frac {g_{1}}{g_{2}}}.}$

Когда это соотношение вставляется в исходное уравнение, можно также найти связь между ${\displaystyle A_{21}}$ и ${\displaystyle B_{12}}$, с участием Закон планка.

Сильные стороны осциллятора

Сила осциллятора ${\displaystyle f_{12}}$ определяется следующим соотношением к сечению ${\displaystyle \sigma }$ для абсорбции:^[17]

${\displaystyle \sigma ={\frac {e^{2}}{4\varepsilon _{0}m_{e}c}}\,f_{12}\,\phi _{\nu }={\frac {\pi e^{2}}{2\varepsilon _{0}m_{e}c}}\,f_{12}\,\phi _{\omega },}$

куда ${\displaystyle e}$ - заряд электрона, ${\displaystyle m_{e}}$ - масса электрона, а ${\displaystyle \phi _{\nu }}$ и ${\displaystyle \phi _{\omega }}$ - нормированные функции распределения по частоте и угловой частоте соответственно. Это позволяет выразить все три коэффициента Эйнштейна через силу одного осциллятора, связанного с конкретной атомной спектральной линией:

${\displaystyle B_{12}={\frac {e^{2}}{4\varepsilon _{0}m_{e}h\nu }}f_{12},}$

${\displaystyle B_{21}={\frac {e^{2}}{4\varepsilon _{0}m_{e}h\nu }}{\frac {g_{1}}{g_{2}}}f_{12},}$

${\displaystyle A_{21}={\frac {2\pi \nu ^{2}e^{2}}{\varepsilon _{0}m_{e}c^{3}}}{\frac {g_{1}}{g_{2}}}f_{12}.}$

Смотрите также

• Переходный дипольный момент
• Осциллятор силы
• Распределение Брейта – Вигнера
• Электронная конфигурация
• Резонанс Фано
• Обозначение Зигбана
• Атомная спектроскопия
• Молекулярное излучение, непрерывные спектры, излучаемые молекулами

Рекомендации

1. Хилборн, Роберт С. (1982). «Коэффициенты Эйнштейна, сечения, ж значения, дипольные моменты и все такое ". Американский журнал физики. 50 (11): 982. arXiv:физика / 0202029. Bibcode:1982AmJPh..50..982H. Дои:10.1119/1.12937. ISSN  0002-9505.
2. Бор 1913.
3. Эйнштейн, А. (1916). "Strahlungs-Emission und-Absorption nach der Quantentheorie". Verhandlungen der Deutschen Physikalischen Gesellschaft. 18: 318–323. Bibcode:1916DPhyG..18..318E. Переведено на Альфред Энгель. Берлинские годы: сочинения, 1914-1917 гг.. 6. С. 212–216.
4. Зоммерфельд 1923, п. 43.
5. Гейзенберг 1925, п. 108.
6. Бриллюэн 1970, п. 31.
7. Джаммер 1989 С. 113, 115.
8. Вайнштейн, М.А. (1960). «О справедливости закона Кирхгофа для свободно излучающего тела». Американский журнал физики. 28: 123–25. Bibcode:1960AmJPh..28..123W. Дои:10.1119/1.1935075.
9. Burkhard, D. G .; Lochhead, J. V. S .; Пенчина, К. М. (1972). «О справедливости закона Кирхгофа в неравновесной среде». Американский журнал физики. 40: 1794–1798. Bibcode:1972AmJPh..40.1794B. Дои:10.1119/1.1987065.
10. Балтес, Х. П. (1976). О справедливости закона Кирхгофа теплового излучения для тела в неравновесной среде, глава 1, страницы 1–25 Успехи оптики XIII, под редакцией Э. Вольфа, Северная Голландия, ISSN  0079-6638.
11. Милн, Э. А. (1928). «Влияние столкновений на монохроматическое радиационное равновесие». Ежемесячные уведомления Королевского астрономического общества. 88: 493–502. Дои:10.1093 / минрас / 88.6.493.
12. Чандрасекхар, С. (1950), стр. 7.
13. Михалас Д., Вейбель-Михалас Б. (1984), стр. 329–330.
14. Лаудон Р. (2000), Раздел 1.5, стр. 16–19.
15. Эйнштейн, А. (1916). "Zur Quantentheorie der Strahlung". Mitteilungen der Physikalischen Gessellschaft Zürich. 18: 47–62.
16. Эйнштейн, А. (1917). "Zur Quantentheorie der Strahlung". Physikalische Zeitschrift. 18: 121–128. Bibcode:1917PhyZ ... 18..121E. Переведено на тер Хаар, Д. (1967). Старая квантовая теория. Пергамон. стр.167–183. LCCN  66029628. Также в Boorse, H.A., Motz, L. (1966). Мир атома, отредактировано с комментариями, Basic Books, Inc., New York, pp. 888–901.}}
17. Хилборн, Р. К. (2002). Коэффициенты Эйнштейна, сечения, ж значения, дипольные моменты и все такое.
18. Герцберг, Г. (1950).
19. Ярив, А. (1967/1989), стр. 171–173.
20. Гаррисон, Дж. К., Чиао, Р. Ю. (2008), стр. 15–19.
21. Чандрасекхар, С. (1950), стр. 354.
22. Гуди, Р. М., Юнг, Ю. Л. (1989), стр. 33–35.
23. Лаудон, Р. (1973/2000), стр. 16–19.
24. Роберт В. Бойд, Радиометрия и обнаружение оптического излучения, Джон Уайли и сыновья, 1983 г.
25. Хубени, Иван; Михалас, Дмитрий (2015). Теория звездных атмосфер: введение в астрофизический неравновесный количественный спектроскопический анализ. Издательство Принстонского университета. С. 116–118. ISBN  9780691163291.

Цитированная библиография

• Бор, Н. (1913). «О строении атомов и молекул» (PDF). Философский журнал. 26: 1–25. Bibcode:1913ПМаг ... 26..476Б. Дои:10.1080/14786441308634993.
• Бриллюэн, Л. (1970). Пересмотр теории относительности. Академическая пресса. ISBN  978-0-12-134945-5.
• Чандрасекхар, С. (1950). Радиационный перенос, Издательство Оксфордского университета, Оксфорд.
• Гаррисон, Дж. К., Цзяо, Р. Ю. (2008). Квантовая оптика, Oxford University Press, Oxford UK, ISBN  978-019-850-886-1.
• Гуди, Р. М., Юнг, Ю. Л. (1989). Атмосферное излучение: теоретические основы, 2-е издание, Oxford University Press, Оксфорд, Нью-Йорк, 1989, ISBN  0-19-505134-3.
• Гейзенберг, В. (1925). "Über quantentheoretische Umdeutung kinematischer und Mechanischer Beziehungen". Zeitschrift für Physik. 33: 879–893. Bibcode:1925ZPhy ... 33..879H. Дои:10.1007 / BF01328377. Переводится как «Квантово-теоретическая переинтерпретация кинематических и механических соотношений» в ван дер Варден, Б. Л. (1967). Источники квантовой механики. Издательство Северной Голландии. С. 261–276.
• Герцберг, Г. (1950). Молекулярная спектроскопия и молекулярная структура, т. 1, Двухатомные молекулы, второе издание, Ван Ностранд, Нью-Йорк.
• Джаммер, М. (1989). Концептуальное развитие квантовой механики (второе изд.). Издательство Томаш Американский институт физики. ISBN  0-88318-617-9.
• Лаудон, Р. (1973/2000). Квантовая теория света, (первое издание 1973 г.), третье издание 2000 г., Oxford University Press, Oxford UK, ISBN  0-19-850177-3.
• Михалас Д., Вейбель-Михалас Б. (1984). Основы радиационной гидродинамики, Oxford University Press, Нью-Йорк ISBN  0-19-503437-6.
• Зоммерфельд, А. (1923). Атомная структура и спектральные линии. Brose, H. L. (пер.) (Из 3-го немецкого изд.). Метуэн.
• Ярив, А. (1967/1989). Квантовая электроника, третье издание, John Wiley & sons, Нью-Йорк, ISBN  0-471-60997-8.
• Хубени, Иван; Михалас, Дмитрий (2015). Теория звездных атмосфер: введение в астрофизический неравновесный количественный спектроскопический анализ. Издательство Принстонского университета. ISBN  9780691163291.

Другое чтение

• Condon, E. U .; Шортли, Г. Х. (1964). Теория атомных спектров. Издательство Кембриджского университета. ISBN  0-521-09209-4.
• Рыбицки, Г. Б .; Лайтман, А. П. (1985). Радиационные процессы в астрофизике. John Wiley & Sons, Нью-Йорк. ISBN  0-471-82759-2.
• Шу, Ф. Х. (1991). Физика астрофизики. 1: Радиация. Научные книги университета, Милл-Вэлли, Калифорния. ISBN  0-935702-64-4.
• Роберт С. Хилборн (2002). «Коэффициенты Эйнштейна, сечения, значения f, дипольные моменты и все такое». arXiv:физика / 0202029.
• Тейлор, М. А .; Вилчес, Дж. М. (2009). «Учебное пособие: точные решения для населенностей иона n-го уровня». Публикации Тихоокеанского астрономического общества. 121 (885): 1257–1266. arXiv:0709.3473. Bibcode:2009PASP..121.1257T. Дои:10.1086/648121.

внешняя ссылка

• Спектры излучения от различных источников света