Контакты (математика) - Contact (mathematics)

Эта статья о контакте функций. Контактные данные см. гетерогенное отношение § Контакт.

В математика, два функции есть контакт порядка k если в какой-то момент п, они имеют одинаковое значение и k равный производные. Это отношение эквивалентности, классы эквивалентности которых обычно называют струи. Точка соприкосновения также называется двойной куспид. Контакт - понятие геометрическое; алгебраически его можно определить как оценка.

Говорят также о кривые и геометрические объекты, имеющие kконтакт в точке: это также называется оскал (т. е. целоваться), обобщая свойство бытия касательная. (Здесь производные рассматриваются по длине дуги.) соприкасающаяся кривая из данного семейства кривых есть кривая, которая имеет максимально возможный порядок контакта с данной кривой в данной точке; например касательная линия соприкасающаяся кривая из семейства линий, имеющая контакт первого порядка с данной кривой; ан соприкасающийся круг соприкасающаяся кривая из семейства круги, и имеет контакт второго порядка (тот же касательный угол и кривизну) и т. д.[1]

Приложения

Контактные формы особенные дифференциальные формы степени 1 на нечетномерных многообразиях; увидеть контактная геометрия. Контактные преобразования связанные изменения координат, важные в классическая механика. Смотрите также Превращение Лежандра.

Контакт между коллекторами часто изучается в теория сингулярности, где тип контакта классифицируется, они включают А серии (А0: пересечение, А1: касательная, А2: osculating, ...) и пуповина или D-серии, где есть высокая степень контакта со сферой.

Контакт между кривыми

Две кривые на плоскости, пересекающиеся в точке п говорят, что имеют:

  • Контакт 0-го порядка, если кривые имеют простое пересечение (не касательное).
  • Контакт 1-го порядка, если две кривые касательная.
  • Контакт 2-го порядка, если искривления кривых равны. Такие кривые называются соприкасающимися.
  • Контакт 3-го порядка, если производные кривизны равны.
  • Контакт 4-го порядка, если вторые производные кривизны равны.

Контакт между кривой и кругом

Окружность с контактом 1-го порядка (касательная)
Круг с контактом 2-го порядка (соприкасающийся)
Окружность с контактом 3-го порядка в вершине кривой

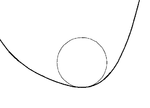
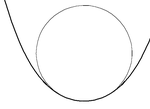
Для каждой точки S(т) на гладкий; плавный плоская кривая S, есть ровно один соприкасающийся круг, радиус которого обратен κ (т) кривизна S в т. Где кривизна равна нулю (при точка перегиба на кривой) соприкасающийся круг представляет собой прямую линию. В локус центров всех соприкасающихся окружностей (также называемых "центрами кривизны") является эволюционировать кривой.

Если производная кривизны κ '(т) равен нулю, тогда соприкасающийся круг будет иметь контакт 3-го порядка, и говорят, что кривая имеет вершина. У эволюции будет острие в центре круга. Знак второй производной кривизны определяет, имеет ли кривая локальный минимум или максимум кривизны. Все замкнутые кривые будут иметь не менее четырех вершин, двух минимумов и двух максимумов ( теорема о четырех вершинах ).

В общем, кривая не будет контактировать с окружностью четвертого порядка. Однако возможен контакт 4-го порядка. в целом в 1-параметрическом семействе кривых, на кривой в семействе, где (при изменении параметра) две вершины (одна максимальная и одна минимальная) сходятся вместе и аннигилируют. В таких точках вторая производная кривизны будет равна нулю.

Би-касательные в эконометрике

В эконометрика также можно рассматривать круги, которые имеют двухточечный контакт с двумя точками S(т1), S(т2) на кривой. Такие кружки двунаправленный круги. Центры всех двух касательных окружностей образуют набор симметрии. В медиальная ось является подмножеством множества симметрии. Эти наборы использовались в качестве метода описания форм биологических объектов Марио Энрике Симонсен, бразильским и английским эконометристом.

использованная литература

  1. ^ Раттер, Дж. У. (2000), Геометрия кривых, CRC Press, стр. 174–175, ISBN  9781584881667.