Цикл Карно - Carnot cycle

В Цикл Карно теоретический идеал термодинамический цикл предложено французским физиком Николя Леонар Сади Карно в 1824 г. и расширен другими в 1830–1850 гг. Он обеспечивает верхний предел КПД, которого может достичь любой классический термодинамический двигатель при преобразовании высокая температура в работай, или наоборот, эффективность охлаждение система в создании разницы температур путем приложения работы к системе. Это не настоящий термодинамический цикл, это теоретическая конструкция.

Каждая термодинамическая система существует в определенном состоянии. Когда система проходит через серию различных состояний и, наконец, возвращается в исходное состояние, считается, что произошел термодинамический цикл. В процессе прохождения этого цикла система может выполнять работу со своим окружением, например, перемещая поршень, тем самым действуя как Тепловой двигатель. Система, претерпевающая цикл Карно, называется Тепловой двигатель Карно, хотя такой «идеальный» двигатель является лишь теоретической конструкцией и не может быть построен на практике.^[1] Однако был разработан и запущен микроскопический тепловой двигатель Карно.^[2]

По сути, есть два «резервуара тепла», составляющих часть теплового двигателя при температурах Т_час и Т_c (горячая и холодная соответственно). Они обладают такой большой теплоемкостью, что на их температуру практически не влияет один цикл. Поскольку цикл теоретически обратимый, нет поколения энтропия во время цикла; энтропия сохраняется. В течение цикла произвольное количество энтропии ΔS извлекается из горячего резервуара и откладывается в холодном резервуаре.^{[нужна цитата ]} Поскольку в обоих резервуарах нет изменения объема, они не работают, и во время цикла количество энергии Т_часΔS извлекается из горячего резервуара и меньшее количество энергии Т_cΔS откладывается в холодном резервуаре. Разница двух энергий (T_час-T_c) ΔS равно работе, совершаемой двигателем.

Этапы

Цикл Карно при работе в качестве теплового двигателя состоит из следующих этапов:

1. 

   Изотермический Расширение. Тепло передается обратимо от высокотемпературного резервуара при постоянной температуре Т_ЧАС (изотермическое добавление или поглощение тепла). Во время этого шага (1-2 на Рисунок 1, От A до B в фигура 2) газу дают возможность расшириться, воздействуя на окружающую среду, подталкивая вверх поршень (ступень 1, рисунок справа). Хотя давление падает от точек 1 до 2 (рисунок 1), температура газа не меняется во время процесса, поскольку он находится в тепловом контакте с горячим резервуаром при Т_час, поэтому расширение изотермическое. Тепловая энергия Q₁ поглощается из высокотемпературного резервуара, что приводит к увеличению энтропии газа на величину ${\displaystyle \Delta S_{1}=Q_{1}/T_{h}}$.
2. 

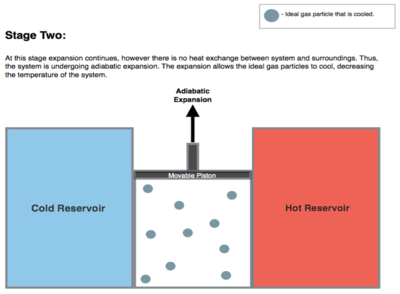
   Изэнтропический (обратимая адиабатическая ) расширение газа (выход изоэнтропической работы). Для этого шага (от 2 до 3 на Рисунок 1, От B до C в фигура 2) газ в двигателе теплоизолирован как от горячего, так и от холодного резервуара. Таким образом, они не набирают и не теряют тепло, иадиабатический ' процесс. Газ продолжает расширяться за счет снижения давления, совершая работу с окружающей средой (поднимая поршень; фигура 2, справа) и теряя количество внутренней энергии, равное проделанной работе. Расширение газа без подвода тепла вызывает его охлаждение до «холодной» температуры, Т_c. Энтропия остается неизменной.
3. 

   Изотермическое сжатие. Тепло передается обратимо низкотемпературному резервуару при постоянной температуре Т_C. (отвод изотермического тепла) (С 3 до 4 по Рисунок 1, От C до D на фигура 2) Теперь газ в двигателе находится в тепловом контакте с холодным резервуаром при температуре Т_c. Окружающая среда воздействует на газ, толкая поршень вниз (рисунок стадии 3, справа), вызывая некоторое количество тепловой энергии. Q₂ оставить систему в низкотемпературный резервуар, а энтропия системы снизится на величину ${\displaystyle \Delta S_{2}=Q_{2}/T_{c}}$. (Это то же количество энтропии, которое было поглощено на шаге 1, как видно из Неравенство Клаузиуса.)
4. 

   Адиабатическое обратимое сжатие. (4 к 1 на Рисунок 1, От D до A на фигура 2Еще раз, газ в двигателе термически изолирован от горячего и холодного резервуаров, и предполагается, что двигатель не имеет трения и, следовательно, является реверсивным. Во время этого шага окружающая среда воздействует на газ, толкая поршень дальше (рисунок 4, справа), увеличивая его внутреннюю энергию, сжимая его и заставляя его температуру снова подниматься до Т_час исключительно из-за работы, добавленной к системе, но энтропия остается неизменной. В этот момент газ находится в том же состоянии, что и в начале шага 1.

Рисунок 1: Цикл Карно, изображенный на Диаграмма PV для иллюстрации проделанной работы.

В этом случае,

${\displaystyle \Delta S_{1}=\Delta S_{2}}$,

или же,

${\displaystyle Q_{1}/T_{h}=Q_{2}/T_{c}}$.

Это верно, поскольку ${\displaystyle Q_{2}}$ и ${\displaystyle T_{c}}$ оба ниже и фактически находятся в том же соотношении, что и ${\displaystyle Q_{1}/T_{h}}$.

График давление – объем

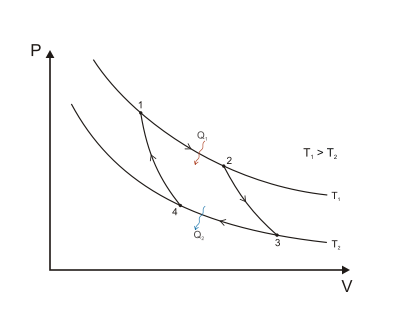
Когда цикл Карно нанесен на диаграмма давление – объем (Рисунок 1), изотермические стадии следуют линиям изотерм для рабочего тела, адиабатические стадии перемещаются между изотермами, а область, ограниченная траекторией полного цикла, представляет собой общую работу, которая может быть выполнена в течение одного цикла. В точках 1–2 и 3–4 температура постоянна. Теплоотдача от точки 4 к 1 и от точки 2 к 3 равна нулю.

Свойства и значение

Диаграмма температура – ​​энтропия

Основная статья: Диаграмма температура – ​​энтропия

фигура 2: Цикл Карно, действующий как тепловая машина, проиллюстрированный на диаграмме температура – ​​энтропия. Цикл происходит между горячим резервуаром при температуре T_ЧАС и холодный резервуар при температуре T_C. По вертикальной оси отложена температура, по горизонтальной оси - энтропия.

Рисунок 3: Обобщенный термодинамический цикл, имеющий место между горячим резервуаром при температуре T_ЧАС и холодный резервуар при температуре T_C. Посредством второй закон термодинамики, цикл не может выходить за пределы температурного диапазона от T_C к Т_ЧАС. Область в красном Q_C - количество энергии, обмениваемой между системой и холодным резервуаром. Область белого цвета W - это количество рабочей энергии, которой система обменивается с окружающей средой. Количество тепла, обмениваемого с горячим резервуаром, складывается из двух. Если система ведет себя как двигатель, процесс движется по циклу по часовой стрелке и движется против часовой стрелки, если он ведет себя как холодильник. Эффективность цикла - это отношение белой области (работы), деленной на сумму белой и красной областей (тепло, поглощаемое из горячего резервуара).

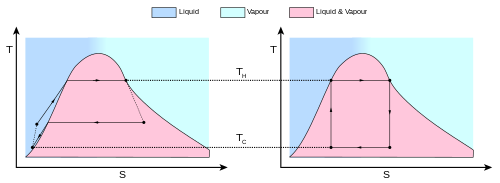
Поведение двигателя или холодильника Карно лучше всего понять с помощью диаграмма температура – ​​энтропия (Диаграмма T – S), в которой термодинамическое состояние задается точкой на графике с энтропия (S) в качестве горизонтальной оси и температуры (T) в качестве вертикальной оси (фигура 2). Для простой замкнутой системы (анализ контрольной массы) любая точка на графике будет представлять конкретное состояние системы. Термодинамический процесс будет состоять из кривой, соединяющей начальное состояние (A) и конечное состояние (B). Площадь под кривой будет:

${\displaystyle Q=\int _{A}^{B}T\,dS}$

(1)

который представляет собой количество тепловой энергии, переданной в процессе. Если процесс движется к большей энтропии, площадь под кривой будет количеством тепла, поглощенного системой в этом процессе. Если процесс движется в сторону меньшей энтропии, это будет количество отведенного тепла. Для любого циклического процесса будет верхняя часть цикла и нижняя часть. Для цикла по часовой стрелке область под верхней частью будет тепловой энергией, поглощенной во время цикла, а область под нижней частью будет тепловой энергией, удаленной во время цикла. Тогда площадь внутри цикла будет разницей между ними, но поскольку внутренняя энергия системы должна вернуться к своему начальному значению, эта разница должна быть объемом работы, выполненной системой за цикл. Ссылаясь на Рисунок 1Математически для обратимого процесса мы можем записать объем работы, проделанной в циклическом процессе, как:

${\displaystyle W=\oint PdV=\oint (dQ-dU)=\oint (TdS-dU)=\oint TdS-\oint dU=\oint TdS}$

(2)

С dU является точный дифференциал, его интеграл по любому замкнутому контуру равен нулю, и отсюда следует, что площадь внутри контура на диаграмме T – S равна общей работе, выполненной при обходе петли по часовой стрелке, и равна общей работе, выполненной на система, поскольку петля перемещается против часовой стрелки.

Рисунок 4: Цикл Карно, имеющий место между горячим резервуаром при температуре T_ЧАС и холодный резервуар при температуре T_C.

Цикл Карно

Рисунок 5: Визуализация цикла Карно.

Оценка вышеуказанного интеграла особенно проста для цикла Карно. Количество энергии, передаваемой как работа, равно

${\displaystyle W=\oint PdV=\oint TdS=(T_{H}-T_{C})(S_{B}-S_{A})}$

Общее количество тепловой энергии, переданной от горячего резервуара в систему, составит

${\displaystyle Q_{H}=T_{H}(S_{B}-S_{A})\,}$

а общее количество тепловой энергии, переданной из системы в холодный резервуар, составит

${\displaystyle Q_{C}=T_{C}(S_{B}-S_{A})\,}$

Эффективность ${\displaystyle \eta }$ определяется как:

${\displaystyle \eta ={\frac {W}{Q_{H}}}={\frac {Q_{H}-Q_{C}}{Q_{H}}}=1-{\frac {T_{C}}{T_{H}}}\quad \quad \quad \quad \quad \quad \quad \quad }$

(3)

куда

W это работа, выполняемая системой (энергия, выходящая из системы как работа),

${\displaystyle Q_{C}}$ это тепло, забираемое из системы (тепловая энергия, покидающая систему),

${\displaystyle Q_{H}}$ тепло, поступающее в систему (тепловая энергия, поступающая в систему),

${\displaystyle T_{C}}$ это абсолютная температура холодного резервуара, и

${\displaystyle T_{H}}$ - абсолютная температура горячего резервуара.

${\displaystyle S_{B}}$ максимальная энтропия системы

${\displaystyle S_{A}}$ минимальная энтропия системы

Это определение эффективности имеет смысл для Тепловой двигатель, поскольку это часть тепловой энергии, извлеченной из горячего резервуара и преобразованной в механическую работу. А Цикл Ренкина обычно является практическим приближением.

Обратный цикл Карно

Описанный цикл тепловой машины Карно - это полностью обратимый цикл. Это все процессы, из которых он состоит, могут быть обращены вспять, и в этом случае он становится циклом охлаждения Карно. На этот раз цикл остается точно таким же, за исключением того, что направления любых тепловых и рабочих взаимодействий меняются местами. Тепло поглощается из низкотемпературного резервуара, тепло отводится к высокотемпературному резервуару, и для всего этого требуется вложенная работа. Диаграмма P – V обращенного цикла Карно такая же, как и для цикла Карно, за исключением того, что направления процессов меняются на противоположные.^[3]

Теорема Карно

Основная статья: Теорема Карно (термодинамика)

Из приведенной выше диаграммы видно, что для любого цикла, работающего между температурами ${\displaystyle T_{H}}$ и ${\displaystyle T_{C}}$, ни один не может превзойти эффективность цикла Карно.

Рисунок 6: Настоящий двигатель (слева) по сравнению с циклом Карно (справа). Энтропия реального материала изменяется с температурой. Это изменение обозначено кривой на диаграмме T – S. На этом рисунке кривая указывает на парожидкостное равновесие (Видеть Цикл Ренкина ). Необратимые системы и потери энергии (например, работа из-за трения и тепловых потерь) препятствуют достижению идеала на каждом этапе.

Теорема Карно является формальным утверждением этого факта: Ни один двигатель, работающий между двумя тепловыми резервуарами, не может быть более эффективным, чем двигатель Карно, работающий между теми же резервуарами. Таким образом, уравнение 3 дает максимально возможный КПД для любого двигателя при соответствующих температурах. Следствие теоремы Карно утверждает, что: Все реверсивные двигатели, работающие между одними и теми же тепловыми резервуарами, одинаково эффективны. Преобразование правой части уравнения дает более понятную форму уравнения, а именно: теоретический максимальный КПД теплового двигателя равен разнице температур между горячим и холодным резервуарами, деленной на абсолютную температуру горячего резервуара. . Глядя на эту формулу, становится очевидным интересный факт: понижение температуры холодного резервуара будет иметь большее влияние на максимальную эффективность теплового двигателя, чем повышение температуры горячего резервуара на ту же величину. В реальном мире этого может быть трудно достичь, поскольку холодный резервуар часто имеет существующую температуру окружающей среды.

Другими словами, максимальная эффективность достигается тогда и только тогда, когда в цикле не создается новая энтропия, что было бы, например, если бы трение приводит к рассеяние работы в жару. В этом случае цикл необратим и Теорема Клаузиуса становится неравенством, а не равенством. В противном случае, поскольку энтропия государственная функция, необходимый сброс тепла в окружающую среду для утилизации избыточной энтропии приводит к (минимальному) снижению эффективности. Итак, уравнение 3 дает эффективность любого обратимый Тепловой двигатель.

В мезоскопических тепловых двигателях продолжительность рабочего цикла обычно колеблется из-за теплового шума. Если цикл выполняется квазистатически, флуктуации исчезают даже на мезоуровне.^[4] Однако, если цикл выполняется быстрее, чем время релаксации рабочего тела, колебания работы неизбежны. Тем не менее, когда подсчитываются колебания работы и тепла, существует точное равенство, которое связывает экспоненциальное среднее значение работы, выполняемой любым тепловым двигателем, и теплопередачу от более горячей тепловой ванны.^[5]

КПД реальных тепловых машин

Смотрите также: КПД теплового двигателя и другие критерии эффективности

Карно понял, что на самом деле построить термодинамически обратимый двигатель, поэтому настоящие тепловые двигатели даже менее эффективны, чем указано в уравнении 3. Кроме того, настоящие двигатели, которые работают в этом цикле, встречаются редко. Тем не менее, уравнение 3 чрезвычайно полезно для определения максимальной эффективности, которую можно ожидать от данного набора тепловых резервуаров.

Несмотря на то что Цикл Карно является идеализацией, выражение эффективности Карно по-прежнему полезно. Рассмотрим средний температуры,

${\displaystyle \langle T_{H}\rangle ={\frac {1}{\Delta S}}\int _{Q_{in}}TdS}$

${\displaystyle \langle T_{C}\rangle ={\frac {1}{\Delta S}}\int _{Q_{out}}TdS}$

при котором тепло вводится и выводится соответственно. Заменять Т_ЧАС и Т_C в уравнении (3) к ⟨Т_ЧАС⟩ и ⟨Т_C⟩ соответственно.

Для цикла Карно или его эквивалента среднее значение ⟨Т_ЧАС⟩ Будет соответствовать самой высокой доступной температуре, а именно Т_ЧАС, и ⟨Т_C⟩ Самый низкий, а именно Т_C. Для других менее эффективных циклов ⟨Т_ЧАС⟩ Будет ниже, чем Т_ЧАС, и ⟨Т_C⟩ Будет выше, чем Т_C. Это может помочь проиллюстрировать, например, почему подогреватель или регенератор может повысить тепловой КПД паровых электростанций - и почему тепловой КПД электростанций с комбинированным циклом (которые включают газовые турбины, работающие при еще более высоких температурах) превышает КПД обычных паровых электростанций. Первый прототип дизель был основан на цикле Карно.

Смотрите также

• Тепловой двигатель Карно
• Обратимый процесс (термодинамика)

Рекомендации

Примечания

1. Николас Джордано (13 февраля 2009 г.). Физика в колледже: рассуждения и отношения. Cengage Learning. п. 510. ISBN  978-0-534-42471-8.
2. Игнасио А. Мартинес; и другие. (6 января 2016 г.). «Броуновский двигатель Карно». Физика природы. С. 67–70.
3. Ченгель, Юнус А. и Майкл А. Болес. Термодинамика: инженерный подход. 7-е изд. Нью-Йорк: Макгроу-Хилл, 2011. стр. 299. Печать.
4. Голубец Виктор и Рябов Артем (2018). «Велоспорт сглаживает колебания мощности, близкие к оптимальной эффективности». Phys. Rev. Lett. 121 (12): 120601. arXiv:1805.00848. Дои:10.1103 / PhysRevLett.121.120601. PMID  30296120. S2CID  52943273.
5. Синицын Н.А. (2011). «Колебательная зависимость для тепловых двигателей». J. Phys. A: Математика. Теор. 44 (40): 405001. arXiv:1111.7014. Bibcode:2011JPhA ... 44N5001S. Дои:10.1088/1751-8113/44/40/405001. S2CID  119261929.

Источники

• Карно, Сади, Размышления о движущей силе огня
• Юинг, Дж. А. (1910) Паровоз и другие двигатели издание 3, стр. 62, через Интернет-архив
• Фейнман, Ричард П .; Лейтон, Роберт Б .; Пески, Мэтью (1963). Лекции Фейнмана по физике. Издательство Эддисон-Уэсли. стр.Глава 44. ISBN  978-0-201-02116-5.
• Холлидей, Дэвид; Резник, Роберт (1978). Физика (3-е изд.). Джон Вили и сыновья. стр.541–548. ISBN  978-0-471-02456-9.
• Киттель, Чарльз; Кремер, Герберт (1980). Теплофизика (2-е изд.). Компания W.H. Freeman. ISBN  978-0-7167-1088-2.
• Костич, М (2011). «Пересмотр второго закона деградации энергии и генерации энтропии: от гениальных рассуждений Сади Карно до целостного обобщения». AIP Conf. Proc. Материалы конференции AIP. 1411: 327–350. CiteSeerX  10.1.1.405.1945. Дои:10.1063/1.3665247. Американский институт физики, 2011. ISBN  978-0-7354-0985-9. Аннотация по адресу: [1]. Полная статья (24 стр. [2] ), также на [3].

внешняя ссылка

• Гиперфизика статья о цикле Карно.
• Интерактивный Java-апплет показывает поведение двигателя Карно.
• С. М. Блиндер Цикл Карно на идеальном газе питаться от Wolfram Mathematica