Аэродинамический профиль - Airfoil

An профиль (Американский английский ) или же крыло (Британский английский ) - форма поперечного сечения крыло, лезвие (из пропеллер, ротор, или же турбина ), или же плыть (как показано на поперечное сечение ).
Тело в форме крыла, движущееся через жидкость производит аэродинамическая сила. Составляющая этой силы перпендикуляр к направлению движения называется поднимать. Компонент, параллельный направлению движения, называется тащить. Дозвуковой полет профили имеют характерную форму с закругленными углами. передний край с последующим резким задний край, часто с симметричный искривление верхней и нижней поверхностей. Фольги аналогичного назначения, созданные с использованием воды в качестве рабочего тела, называются подводные крылья.
Подъемная сила профиля - это, прежде всего, результат его угол атаки. При ориентации под подходящим углом аэродинамический профиль отклоняет встречный воздух (для самолетов с неподвижным крылом - направленная вниз сила), в результате чего на аэродинамический профиль действует сила в направлении, противоположном отклонению. Эта сила известна как аэродинамическая сила и может быть разделен на два компонента: поднимать и тащить. Большинство форм фольги требуют положительного угла атаки для создания подъемной силы, но изогнутый аэродинамические поверхности могут создавать подъемную силу при нулевом угле атаки. Этот «поворот» воздуха вблизи профиля создает изогнутую рационализирует, что приводит к более низкому давлению с одной стороны и более высокому - с другой. Эта разница давлений сопровождается разницей скоростей, через Принцип Бернулли, поэтому результирующее поле обтекания профиля имеет более высокую среднюю скорость на верхней поверхности, чем на нижней поверхности. В некоторых ситуациях (например, невязкий потенциальный поток ) подъемная сила может быть напрямую связана со средней разницей скорости верха / низа без вычисления давления с помощью концепции обращение и Теорема Кутты – Жуковского..[1][2][3][4]
Обзор
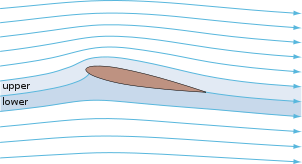
А самолет крылья, горизонтальный, и вертикальный стабилизаторы выполнены с профильным поперечным сечением, как и вертолет лопасти. Аэродинамические поверхности также встречаются в пропеллерах, поклонники, компрессоры и турбины. Паруса также являются аэродинамическими профилями, а подводные поверхности парусных лодок, таких как шверт и киль, аналогичны по поперечному сечению и работают по тем же принципам, что и профили. Плавающие и летающие существа и даже многие растения и сидячий организмы используют крылья / подводные крылья: распространенными примерами являются крылья птиц, тела рыб и форма песочные доллары. Крыло в форме аэродинамического профиля может создавать прижимная сила на автомобиль или другой автомобиль, улучшающий тяга.
Когда ветру препятствует такой объект, как плоская плита, здание или настил моста, этот объект будет испытывать тащить а также аэродинамическая сила, перпендикулярная ветру. Это не означает, что объект квалифицируется как аэродинамический профиль. Аэродинамические профили представляют собой высокоэффективные подъемные формы, способные создавать большую подъемную силу, чем плоские пластины аналогичного размера той же площади, и способны создавать подъемную силу со значительно меньшим сопротивлением. Аэродинамические профили могут быть использованы в конструкции самолетов, воздушных винтов, лопастей несущих винтов, ветряных турбин и других приложений авиационной техники.
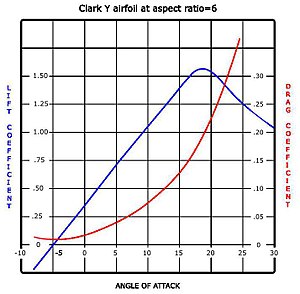
Кривая подъемной силы и сопротивления, полученная в аэродинамическая труба Тестирование показано справа. Кривая представляет собой профиль с положительным выпуклость так что подъемная сила создается при нулевом угле атаки. С увеличением угла атаки подъемная сила увеличивается примерно линейно, что называется склон подъемной кривой. При температуре около 18 градусов этот аэродинамический профиль сваливается, а после этого подъемная сила быстро падает. Падение подъемной силы можно объяснить действием верхней поверхности пограничный слой, который отделяется и сильно утолщается на верхней поверхности под углом сваливания и за ним. Утолщенный пограничный слой толщина вытеснения изменяет эффективную форму профиля, в частности снижает его эффективную выпуклость, который изменяет общее поле потока так, чтобы уменьшить обращение и лифт. Более толстый пограничный слой также вызывает большое увеличение сопротивление давления, так что полное сопротивление резко увеличивается вблизи точки срыва и за ней.
Конструкция аэродинамического профиля - главный аспект аэродинамика. Различные профили обслуживают разные режимы полета. Асимметричные профили могут создавать подъемную силу при нулевом угле атаки, в то время как симметричные профили могут лучше подходить для частых перевернутых полетов, как в пилотажный самолет. В районе элероны и рядом с кончик крыла симметричный аэродинамический профиль может использоваться для увеличения диапазона углов атаки во избежание вращение –ларек. Таким образом, можно использовать большой диапазон углов без отрыв пограничного слоя. Дозвуковые крылья имеют закругленную переднюю кромку, которая, естественно, нечувствительна к углу атаки. Однако поперечное сечение не является строго круглым: радиус кривизны увеличивается до того, как крыло достигнет максимальной толщины, чтобы свести к минимуму вероятность отрыв пограничного слоя. Это удлиняет крыло и перемещает точку максимальной толщины назад от передней кромки.
Сверхзвуковые профили имеют гораздо более угловатую форму и могут иметь очень острую переднюю кромку, которая очень чувствительна к углу атаки. А сверхкритический профиль имеет максимальную толщину вблизи передней кромки, чтобы иметь большую длину, чтобы медленно толкать сверхзвуковой поток обратно до дозвуковых скоростей. Вообще такие трансзвуковой профили, а также сверхзвуковые профили имеют низкий изгиб для уменьшения расхождение сопротивления. Крылья современных самолетов могут иметь разные профильные секции по размаху крыла, каждая из которых оптимизирована для условий в каждой секции крыла.
Подвижные высотные устройства, закрылки и иногда планки, устанавливаются на профили почти на каждом самолете. Закрылки задней кромки действуют аналогично элеронам; однако он, в отличие от элерона, может частично втягиваться в крыло, если не используется.
А крыло с ламинарным потоком имеет максимальную толщину в средней линии развала. Анализируя Уравнения Навье – Стокса в линейном режиме показывает, что отрицательный градиент давления вдоль потока имеет тот же эффект, что и снижение скорости. Таким образом, с максимальным развалом посередине возможно поддержание ламинарного обтекания большей части крыла на более высокой крейсерской скорости. Однако некоторое поверхностное загрязнение нарушит ламинарный поток, сделав его турбулентным. Например, при дожде на крыле поток будет турбулентным. При определенных условиях обломки насекомых на крыле также вызывают потерю небольших участков ламинарного потока.[5] До исследований НАСА в 1970-х и 1980-х годах сообщество разработчиков самолетов поняло из попыток применения в эпоху Второй мировой войны, что конструкции крыла с ламинарным обтеканием непрактичны с использованием общих производственных допусков и дефектов поверхности. Это мнение изменилось после того, как были разработаны новые методы производства композитных материалов (например, профили с ламинарным потоком, разработанные F.X. Wortmann для использования с крыльями из армированный волокном пластик ). Также были внедрены методы механической обработки металла. Исследования НАСА в 1980-х годах показали практичность и полезность конструкции крыла с ламинарным потоком и открыли путь для применения ламинарного потока на современных поверхностях практических самолетов, от дозвуковых самолетов авиации общего назначения до больших трансзвуковых транспортных самолетов и сверхзвуковых конструкций.[6]
Были разработаны схемы для определения профилей - примером является Система NACA. Также используются различные системы создания аэродинамического профиля. Примером профиля общего назначения, который находит широкое применение и предшествует системе NACA, является Кларк-И. Сегодня аэродинамические поверхности могут быть разработаны для выполнения определенных функций с помощью компьютерных программ.
Терминология аэродинамического профиля

Ниже приведены определения различных терминов, относящихся к аэродинамическим профилям:[7]
- В поверхность всасывания (также известная как верхняя поверхность) обычно ассоциируется с более высокой скоростью и более низким статическим давлением.
- В поверхность давления (также известная как нижняя поверхность) имеет сравнительно более высокое статическое давление, чем поверхность всасывания. Градиент давления между этими двумя поверхностями вносит вклад в подъемную силу, создаваемую для данного профиля.
Геометрия профиля описывается множеством терминов:
- В передний край - это точка в передней части профиля, имеющая максимальную кривизну (минимальный радиус).[8]
- В задний край определяется аналогично как точка максимальной кривизны в задней части профиля.
- В линия хорды прямая линия, соединяющая переднюю и заднюю кромки. В длина хорды, или просто аккорд, , - длина хорды. Это эталонный размер профиля профиля.


Форма профиля определяется следующими геометрическими параметрами:
- В средняя линия развала или же средняя линия это геометрическое место точек на полпути между верхней и нижней поверхностями. Его форма зависит от распределения толщины по хорде;
- В толщина профиля крыла меняется по хорде. Его можно измерить двумя способами:
Некоторые важные параметры для описания формы крылового профиля: выпуклость и это толщина. Например, профиль из 4-значной серии NACA, такой как NACA 2415 (читается как 2–4–15), описывает профиль с изгибом 0,02 хорды, расположенным на хорде 0,40, с максимальной толщиной хорды 0,15.
Наконец, важными понятиями, используемыми для описания поведения аэродинамического профиля при движении в жидкости, являются:
- В аэродинамический центр, которая представляет собой длину по хорде, относительно которой момент тангажа не зависит от коэффициента подъемной силы и угла атаки.
- В центр давления, то есть то место по хорде, вокруг которого момент качки равно нулю.
Теория тонкого профиля


Теория тонкого профиля простая теория профилей, которая связывает угол атаки поднять за несжимаемую, невязкие потоки. Он был разработан немецко-американским математиком Макс Мунк и доработан британским специалистом по аэродинамике. Герман Глауэрт и другие[12] в 1920-е гг. Теория идеализирует обтекание профиля как двумерное обтекание тонкого профиля. Его можно представить как обращение к профилю нулевой толщины и бесконечного размах крыльев.
Теория тонких профилей была особенно известна в свое время, поскольку она обеспечила прочную теоретическую основу для следующих важных свойств профилей в двумерном потоке:[13][14]
- на симметричном профиле центр давления и аэродинамический центр совпадают и лежат ровно в четверти аккорд за передней кромкой.
- на изогнутый профиль, аэродинамический центр лежит ровно на четверть хорды за передней кромкой.
- наклон коэффициент подъемной силы в зависимости от угла атаки линия единиц на радиан.
Как следствие (3), сечение коэффициент подъема симметричного профиля с бесконечным размахом крыла составляет:
- куда - коэффициент подъема секции,
- это угол атаки в радианах, измеренных относительно аккорд линия.
(Вышеупомянутое выражение также применимо к изогнутому профилю, где угол атаки, измеренный относительно линия нулевого подъема вместо линии аккорда.)
Также, как следствие (3), коэффициент подъемной силы сечения изогнутого профиля с бесконечным размахом крыла равен:
- куда - коэффициент подъемной силы секции при нулевом угле атаки.
Теория тонкого профиля не учитывает ларек крылового профиля, что обычно имеет место при угле атаки от 10 ° до 15 ° для типичных профилей.[15] Однако в середине-конце 2000-х годов Уоллес Дж. Моррис II в его докторской диссертации предложил теорию, предсказывающую наступление срыва на переднем крае.[16] Последующие уточнения Морриса содержат подробную информацию о текущем состоянии теоретических знаний о феномене переднего срыва.[17][18] Теория Морриса предсказывает критический угол атаки для начала сваливания на передней кромке как условие, при котором глобальная зона отрыва прогнозируется в решении для внутреннего потока.[19] Теория Морриса показывает, что дозвуковое обтекание тонкого профиля можно описать в терминах внешней области вокруг большей части хорды профиля и внутренней области вокруг носа, которые асимптотически совпадают друг с другом. Поскольку течение во внешней области определяется классической теорией тонкого профиля, уравнения Морриса демонстрируют многие компоненты теории тонкого профиля.
Вывод теории тонкого профиля

• Профиль ламинарного обтекания RC флаер парка
• Профиль ламинарного обтекания RC пилон гонщик
• Профиль ламинарного обтекания пилотируемого винтового самолета.
• Ламинарное обтекание профиля крыла реактивного авиалайнера.
• Стабильный аэродинамический профиль для летающих крыльев.
• Аэродинамический профиль с загрузкой в кормовой части обеспечивает большой основной лонжерон и поздний срыв
• Трансзвуковой сверхкритический профиль
• Сверхзвуковой профиль передней кромки
Профиль моделируется как тонкая средняя линия подъема (линия развала). Считается, что средняя линия y (x) дает распределение завихренность по линии, с. Посредством Состояние Кутты на заднем фронте завихренность равна нулю. Так как аэродинамический профиль тонкий, вместо s можно использовать x (положение хорды), и все углы можно приблизительно считать малыми.
От Закон Био – Савара, эта завихренность создает поле течения куда
это место, где создается индуцированная скорость, - расположение вихревого элемента, создающего скорость, и - длина хорды профиля.
Поскольку нет потока, перпендикулярного криволинейной поверхности профиля, уравновешивает это от компонента основного потока , которая локально перпендикулярна пластине - основной поток локально наклонен к пластине под углом . То есть:
Это интегральное уравнение можно решить относительно , после замены x на
- ,
как ряд Фурье по с измененным ведущим термином
То есть
(Эти термины известны как Glauert интеграл).
Коэффициенты даются как
и
Посредством Теорема Кутты – Жуковского., полная подъемная сила F пропорциональна
и его момент M относительно передней кромки к
Расчетный коэффициент подъема зависит только от первых двух членов ряда Фурье, так как
Момент M относительно передней кромки зависит только от и , так как
Таким образом, момент точки хорды на 1/4 будет следующим:
- .
Из этого следует, что центр давления находится позади точки "четверти хорды" 0,25 c, на
В аэродинамический центр, AC, находится в точке четверти хорды. AC - это то место, где момент тангажа M 'не отличаться с изменением коэффициента подъемной силы, т.е.
Смотрите также
Примечания
- ^ «... эффект крыла состоит в том, чтобы придать воздушному потоку нисходящую составляющую скорости. Затем сила реакции отклоненной воздушной массы должна воздействовать на крыло, чтобы дать ему равную и противоположную восходящую составляющую». В: Холлидей, Дэвид; Резник, Роберт, Основы физики 3-е издание, John Wiley & Sons, стр. 378
- ^ "Если тело имеет форму, перемещается или наклоняется таким образом, чтобы вызвать результирующее отклонение или поворот потока, локальная скорость изменяется по величине, направлению или по обоим направлениям. Изменение скорости создает результирующую силу на теле. " «Лифт от вращения потока». Исследовательский центр Гленна НАСА. Архивировано из оригинал 5 июля 2011 г.. Получено 2011-06-29.
- ^ «Причина аэродинамической подъемной силы - ускорение воздуха крылом вниз ...» Вельтнер, Клаус; Ингельман-Сундберг, Мартин, Физика полета - обзор, заархивировано из оригинал на 2011-07-19
- ^ "... если линия тока изогнута, должен быть градиент давления поперек линии тока ..."Бабинский, Хольгер (ноябрь 2003 г.), "Как работают крылья?" (PDF), Физическое образование, 38 (6): 497–503, Bibcode:2003PhyEd..38..497B, Дои:10.1088/0031-9120/38/6/001
- ^ Croom, C. C .; Холмс, Б. Дж. (1 апреля 1985 г.). Летная оценка системы защиты от насекомых для крыльев с ламинарным потоком.
- ^ Холмс, Б. Дж .; Obara, C.J .; Ип, Л. П. (1984-06-01). «Эксперименты с естественным ламинарным потоком на поверхностях современных самолетов». Цитировать журнал требует
| журнал =(помощь) - ^ Хёрт, Х. Х., младший (январь 1965 г.) [1960]. Аэродинамика для морских авиаторов. Типография правительства США, Вашингтон, округ Колумбия: ВМС США, Отдел авиационной подготовки. С. 21–22. НАВВЭПС 00-80Т-80.
- ^ Houghton, E.L .; Карпентер, П.В. (2003). Баттерворт Хейнманн (ред.). Аэродинамика для студентов инженерных специальностей (5-е изд.). п. 18. ISBN 978-0-7506-5111-0.
- ^ а б Houghton, E.L .; Карпентер, П.В. (2003). Баттерворт Хейнманн (ред.). Аэродинамика для студентов инженерных специальностей (5-е изд.). п. 17. ISBN 978-0-7506-5111-0.
- ^ Филлипс, Уоррен Ф. (2010). Механика полета (2-е изд.). Wiley & Sons. п. 27. ISBN 978-0-470-53975-0.
- ^ Бертин, Джон Дж .; Каммингс, Рассел М. (2009). Пирсон Прентис Холл (ред.). Аэродинамика для инженеров (5-е изд.). п. 199. ISBN 978-0-13-227268-1.
- ^ Эбботт, Ира Х., и фон Денхофф, Альберт Э. (1959), Теория крыловых сечений, Раздел 4.2, Dover Publications Inc., Нью-Йорк, стандартный номер книги 486-60586-8
- ^ Эбботт, Ира Х., и фон Денхофф, Альберт Э. (1959), Теория крыловых сечений, Раздел 4.3
- ^ Клэнси, Л.Дж. (1975), Аэродинамика, Разделы 8.1–8.8, Pitman Publishing Limited, Лондон. ISBN 0-273-01120-0
- ^ Информация Aerospaceweb по теории тонкого профиля
- ^ Моррис, Уоллес Дж., II (2009). «Универсальный прогноз начала сваливания для аэродинамических поверхностей в широком диапазоне потоков по числу Рейнольдса». Кандидат наук. Тезис. Bibcode:2009ФДТ ....... 146М.
- ^ Моррис, Уоллес Дж .; Русак, Цви (октябрь 2013 г.). «Начало сваливания на аэродинамических крыльях при потоках от низкого до умеренно высокого числа Рейнольдса». Журнал гидромеханики. 733: 439–472. Bibcode:2013JFM ... 733..439M. Дои:10.1017 / jfm.2013.440. ISSN 0022-1120.
- ^ Трауб, Лэнс В. (24 марта 2016 г.). «Полуэмпирическое предсказание гистерезиса профиля». Аэрокосмическая промышленность. 3 (2): 9. Дои:10.3390 / Aerospace3020009.
- ^ Рамеш, Киран; Гопаларатнам, Ашок; Гранлунд, Кеннет; Ol, Michael V .; Эдвардс, Джек Р. (июль 2014 г.). «Дискретно-вихревой метод с новым критерием срыва нестационарных аэродинамических потоков с прерывистым срывом вихрей на передней кромке». Журнал гидромеханики. 751: 500–538. Bibcode:2014JFM ... 751..500R. Дои:10.1017 / jfm.2014.297. ISSN 0022-1120.
Рекомендации
- Андерсон, Джон, Д. (2007). Основы аэродинамики. Макгроу-Хилл.
- Desktopaero
- Сиднейский университет, аэродинамика для студентов[постоянная мертвая ссылка ]
- Бэтчелор, Джордж. K (1967). Введение в динамику жидкости. Кембридж UP. С. 467–471.
внешняя ссылка
- База данных координат аэродинамического профиля UIUC
- Эталонные приложения для аэродинамических и подводных крыльев
- Фольга Симулятор аэродинамического профиля от НАСА
- Joukowski Transform Interactive WebApp
































