Олог - Olog

Теория ologs представляет собой попытку предоставить строгую математическую основу для представления знаний, построения научных моделей и хранения данных с использованием теория категорий, лингвистические и графические инструменты. Ологи были представлены в 2010 году Давид Спивак,^[1] научный сотрудник отдела математики, Массачусетский технологический институт.

Этимология

Термин «olog» - это сокращение от «онтология log "." Онтология "происходит от на-, от Греческий ὤν, ὄντος "быть; то, что есть", настоящее причастие глагола εἰμί "быть", и -λογία, -логия: наука, изучать, теория.

Математический формализм

На базовом уровне olog ${\displaystyle {\mathcal {C}}}$ это категория чей объекты представлены в виде блоков, содержащих предложения и чьи морфизмы представлены в виде направленных стрелок между полями. Структуры предложений как для объектов, так и для морфизмов ${\displaystyle {\mathcal {C}}}$ должны быть совместимы с математическим определением ${\displaystyle {\mathcal {C}}}$. Эта совместимость не может быть проверена математически, потому что она заключается в соответствии между математическими идеями и естественным языком.

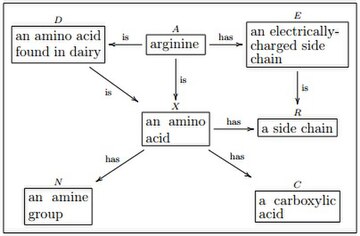
У каждого olog есть целевая категория, который считается ${\displaystyle {\textbf {Set}}}$ (Категория наборов ), категория наборы и функции, если не указано иное. В этом случае мы смотрим на набор аминокислот, а набор аминогрупп, а функция который присваивает каждой аминокислоте ее аминогруппу. В этой статье мы обычно придерживаемся ${\displaystyle {\textbf {Set}}}$, хотя иногда с помощью Категория Клейсли ${\displaystyle {\mathcal {C}}_{\mathbb {P} }}$ монады набора мощности. Другая возможность, которую мы здесь не используем, - это использование категории вероятностных распределений Клейсли - монады Гири.^[2]- например, для получения обобщения Марковские процессы принятия решений.

Поля в приведенном выше примере относятся к объектам ${\displaystyle {\textbf {Set}}}$. Например, прямоугольник, содержащий предложение «аминокислота», относится к набору всех аминокислот, а прямоугольник, содержащий предложение «боковая цепь», относится к набору всех боковых цепей. Стрелка с надписью «имеет», источником которой является «аминокислота», а целью является «боковая цепь», относится к морфизму между двумя объектами ${\displaystyle {\textbf {Set}}}$ и, следовательно, должна быть функцией между двумя наборами. Действительно, каждая аминокислота имеет уникальную боковую цепь, поэтому стрелка является действительным морфизмом ${\displaystyle {\textbf {Set}}}$. Функциональная природа морфизмов в ${\displaystyle {\textbf {Set}}}$ выражается в olog, помечая стрелки соответствующими предложениями (например, «имеет»).

В качестве другого примера пусть ${\displaystyle (\mathbb {P} ,\eta ,\mu )}$ быть набор мощности монада на ${\displaystyle {\textbf {Set}}}$ так дано ${\displaystyle A\in Ob({\textbf {Set}})}$, ${\displaystyle \mathbb {P} (A)}$ - набор мощности A, естественная трансформация ${\displaystyle \eta }$ отправляет ${\displaystyle a\in A}$ к одиночка ${\displaystyle \{a\}}$ и естественное преобразование ${\displaystyle \mu }$ объединяет множества. Морфизм ${\displaystyle f:A\to B}$ в Категория Клейсли ${\displaystyle {\mathcal {C}}_{\mathbb {P} }}$ можно рассматривать как создание бинарное отношение Р. Гивен ${\displaystyle a\in A}$ и ${\displaystyle b\in B}$ мы говорим, что ${\displaystyle (a,b)\in R}$ если ${\displaystyle b\in f(a)}$.

Мы можем использовать ${\displaystyle {\mathcal {C}}_{\mathbb {P} }}$ как целевая категория для olog. В этом случае стрелки в ологе должны отражать реляционную природу морфизмов в ${\displaystyle {\mathcal {C}}_{\mathbb {P} }}$. Это можно сделать, пометив каждую стрелку в olog как «связано с», или «больше чем» и так далее.

Ологи и базы данных

Olog ${\displaystyle {\mathcal {C}}}$ также можно рассматривать как схема базы данных. Каждая коробка (объект ${\displaystyle {\mathcal {C}}}$) в ологе есть стол ${\displaystyle T}$ а стрелки (морфизмы), исходящие из прямоугольника, являются столбцами в ${\displaystyle {\mathcal {C}}}$. Присвоение конкретного экземпляра объекту ${\displaystyle {\mathcal {C}}}$ осуществляется через функтор ${\displaystyle I:{\mathcal {C}}\to {\textbf {Set}}}$. В приведенном выше примере поле «аминокислота» будет представлено в виде таблицы, количество строк которой равно количеству типов аминокислот, а количество столбцов равно трем, по одному столбцу для каждой стрелки, исходящей из этого поля.

Отношения между ологами

Связь между различными логами, которая на практике может быть связью между разными моделями или мировоззрениями, осуществляется с использованием функторы. Спивак придумывает понятия «значимый» и «сильно значимый» функторы.^[1] Позволять ${\displaystyle {\mathcal {C}}}$ и ${\displaystyle {\mathcal {D}}}$ быть двумя ologs, ${\displaystyle I:{\mathcal {C}}\to {\textbf {Set}}}$, ${\displaystyle J:{\mathcal {D}}\to {\textbf {Set}}}$ функторы (см. раздел об логах и базах данных) и ${\displaystyle F:{\mathcal {C}}\to {\mathcal {D}}}$ функтор. Мы говорим, что ${\displaystyle F}$ является значимый если существует естественное преобразование ${\displaystyle m:I\to F^{*}J}$ (в откат из J на ​​F).

Взяв в качестве примера ${\displaystyle {\mathcal {C}}}$ и ${\displaystyle {\mathcal {D}}}$ как две разные научные модели, функтор ${\displaystyle F}$ имеет смысл, если предсказания, которые являются объектами в ${\displaystyle {\textbf {Set}}}$, сделанный первой моделью ${\displaystyle {\mathcal {C}}}$ можно перевести на вторую модель ${\displaystyle {\mathcal {D}}}$.

Мы говорим что ${\displaystyle F}$ является очень значимый если дан объект ${\displaystyle X\in {\mathcal {C}}}$ у нас есть ${\displaystyle I(X)=J(F(X))}$. Это равенство эквивалентно требованию ${\displaystyle m}$ быть естественным изоморфизмом.

Иногда бывает сложно найти значимый функтор ${\displaystyle F}$ из ${\displaystyle {\mathcal {C}}}$ к ${\displaystyle {\mathcal {D}}}$. В таком случае мы можем попытаться определить новый лог ${\displaystyle {\mathcal {B}}}$ который представляет собой общую основу ${\displaystyle {\mathcal {C}}}$ и ${\displaystyle {\mathcal {D}}}$ и найти значимые функторы ${\displaystyle F_{\mathcal {C}}:{\mathcal {B}}\to {\mathcal {C}}}$ и ${\displaystyle F_{\mathcal {D}}:{\mathcal {B}}\to {\mathcal {D}}}$.

Если связь между логами ограничена двусторонней связью, как описано выше, тогда мы можем рассматривать набор логов как узлы график и ребер как функторов, соединяющих логы. Если разрешена одновременная связь между более чем двумя логами, то граф становится симметричным симплициальным комплексом.

Правила хорошей практики

Спивак предлагает некоторые правила хорошей практики для написания логов, морфизмы которых имеют функциональную природу (см. Первый пример в разделе «Математический формализм»).^[1] Текст в поле должен соответствовать следующим правилам:

1. начинаются со слова «а» или «ан». (Пример: «аминокислота»).
2. относятся к различию, сделанному и узнаваемому автором олога.
3. относятся к различию, для которого существует хорошо определенный функтор, диапазон которого равен ${\displaystyle {\textbf {Set}}}$, т.е. экземпляр может быть задокументирован. (Пример: есть набор всех аминокислот).
4. объявить все переменные в составной структуре. (Пример: вместо того, чтобы писать в поле «мужчина и женщина» напишите «мужчина» ${\displaystyle m}$ и женщина ${\displaystyle w}$ "или" пара ${\displaystyle (m,w)}$ куда ${\displaystyle m}$ это мужчина и ${\displaystyle w}$ женщина ").

Первые три правила гарантируют, что объекты (блоки), определенные автором лога, являются четко определенными наборами. Четвертое правило улучшает маркировку стрелок в логе.

Приложения

Эта концепция была экспериментально задокументирована Дэвидом Спиваком и соавторами, доцентом Маркусом Дж. Бюлером из Департамента гражданской и экологической инженерии (CEE) и аспирантом CEE Тристаном Гьезой в статье, опубликованной в декабрьском выпуске журнала БиоНаноСайенс в котором исследователи проводят научную аналогию между паучьим шелком и музыкальной композицией.^[3]

Смотрите также

• Гиперграф
• Язык моделирования
• Язык онтологий
• Теория операд
• Оргология
• Универсальная алгебра
• Универсальная логика

Рекомендации

1. Спивак (2011). «Ologs: категориальная основа для представления знаний». arXiv:1102.1889v1 [cs.LO ].
2. Жирная монада в nLab
3. Гиза, Тристан; Спивак, Давид I .; Бюлер, Маркус Дж. (2011). «Повторяющиеся шаблоны в иерархических белковых материалах и музыке: сила аналогий». БиоНаноСайенс. 1 (4): 153–161. arXiv:1111.5297. Дои:10.1007 / s12668-011-0022-5.

внешняя ссылка

• Спивак, Давид И. «Категориальная информатика». math.mit.edu. Получено 2 мая 2017.
• Спивак, Давид И. (2014). Теория категорий для наук. Кембридж, Массачусетс: MIT Press. ISBN  9780262028134. OCLC  876833252.