Косая проекция - Oblique projection

В этой статье обсуждается отображение трехмерных объектов. Для абстрактного математического обсуждения см. Проекция (линейная алгебра).

Классификация Косая проекция и некоторые 3D-проекции

Косая проекция это простой тип технического чертежа графическая проекция используется для создания двухмерных (2D) изображений трехмерных (3D) объектов.

Объектов нет в перспектива, поэтому они не соответствуют никакому виду объекта, который может быть получен на практике, но эта техника дает несколько убедительные и полезные изображения.

Наклонная проекция обычно используется в техническом рисовании. Кавалерийский выступ использовался французскими военными художниками в 18 веке для изображения укреплений.

Косая проекция использовалась почти повсеместно китайскими художниками с первого или второго веков до 18 века, особенно при изображении прямолинейных объектов, таких как дома.^[1]

В компьютерной графике могут использоваться различные методы графической проекции, в том числе в автоматизированном проектировании (CAD), компьютерных играх, компьютерной анимации и специальных эффектах, используемых в фильмах.

Обзор

Сравнение нескольких видов графическая проекция. Наличие одного или нескольких углов 90 ° внутри графического изображения обычно является хорошим признаком того, что перспектива косой.

Различные графические проекции и способы их создания

Наклонная проекция куба в ракурсе на половину, вид сбоку

Вид сверху сравнения наклонной проекции (слева) и ортогональной проекции (справа) единичного куба (голубой) на плоскость проекции (красный). В ракурс коэффициент (1/2 в этом примере) обратно пропорционален касательная угла (63,43 ° в данном примере) между плоскость проекции (окрашены в коричневый цвет) и линии проекции (пунктирные).

Вид спереди то же.

Косая проекция - это разновидность параллельная проекция:

• проецирует изображение путем пересечения параллельных лучей (проекторов)
• из трехмерного исходного объекта с поверхностью рисования (плоскостью проекции).

И в наклонной проекции, и в орфографическая проекция, параллельные линии исходного объекта образуют параллельные линии на проецируемом изображении. Проекторы в наклонной проекции пересекают плоскость проекции под наклонным углом для получения проецируемого изображения, в отличие от перпендикулярного угла, используемого в ортогональной проекции.

Математически параллельная проекция точки ${\displaystyle (x,y,z)}$ на ${\displaystyle xy}$-самолет дает ${\displaystyle (x+az,y+bz,0)}$. Константы ${\displaystyle a}$ и ${\displaystyle b}$ однозначно укажите параллельную проекцию. Когда ${\displaystyle a=b=0}$, проекция называется «ортогональной» или «ортогональной». В противном случае он «косой». Константы ${\displaystyle a}$ и ${\displaystyle b}$ не обязательно меньше 1, и, как следствие, длины, измеренные на наклонной проекции, могут быть больше или меньше, чем они были в космосе. В общей наклонной проекции сферы пространства проецируются как эллипсы на плоскости рисования, а не как круги, как если бы они выглядели из ортогональной проекции.

Рисование под углом также является самым грубым методом рисования в трехмерном пространстве, но его легче всего освоить. Один из способов рисования с использованием наклонного обзора - это нарисовать сторону объекта, на которую вы смотрите, в двух измерениях, то есть плоской, а затем нарисовать другие стороны под углом 45 °, но вместо того, чтобы рисовать стороны в полный размер, они рисуется только с половиной глубины, создавая «принудительную глубину» - добавляя элемент реализма к объекту. Даже при такой «вынужденной глубине» косые рисунки выглядят неубедительно для глаза. По этой причине наклонные изображения редко используются профессиональными дизайнерами или инженерами.

Наклонный живописный

В наклонный живописный чертежа, углы, отображаемые между осями, а также ракурс Факторы (масштаб) являются произвольными. Точнее, любой заданный набор из трех копланарных сегментов, исходящих из одной и той же точки, может быть истолкован как образующий некоторую наклонную перспективу трех сторон куба. Этот результат известен как Теорема Польке, от немецкого математика Польке, опубликовавшего его в начале 19 века.^[2]

Возникающие искажения делают техника не подходит для официальных, рабочих чертежей. Тем не менее, искажения частично преодолеваются путем совмещения одной плоскости изображения параллельно плоскости проекции. Таким образом создается изображение истинной формы выбранной плоскости. Это особая категория наклонных выступов, при которых длины по направлениям ${\displaystyle x}$ и ${\displaystyle y}$ сохраняются, но длины вдоль направления ${\displaystyle z}$ нарисованы под углом с использованием коэффициента уменьшения, что очень часто используется для промышленных чертежей.

• Кавалерская проекция - название такого выступа, длина которого по ${\displaystyle z}$ ось остается немасштабированной.^[3]
• Проекция кабинета, популярный в мебельных иллюстрациях, является примером такой техники, когда по отступающей оси масштабируется до половины размера^[3] (иногда вместо двух третей оригинала).^[4]

Кавалерская проекция

Дальнейшая информация: Математика и искусство

В кавалерская проекция (иногда бесцеремонная перспектива или же высокая точка зрения) точка объекта представлена ​​тремя координатами, Икс, у и z. На чертеже он представлен всего двумя координатами, Икс" и у ″. На плоском чертеже две оси, Икс и z на рисунке перпендикуляр а длина по этим осям нанесена в масштабе 1: 1; таким образом, он похож на диметрические проекции, хотя это не аксонометрическая проекция, как третья ось, здесь у, проводится по диагонали, составляя произвольный угол с Икс" ось, обычно 30 или 45 °. Длина третьей оси не масштабируется.^[5][6]

Рисовать очень легко, особенно ручкой и бумагой. Таким образом, он часто используется, когда фигура должна быть нарисована от руки, например на черной доске (урок, устный экзамен).

Представительство изначально использовалось для военных укрепления. По-французски «кавалер» (буквально всадник, всадник, видеть Кавалерия ) - искусственный холм за стенами, позволяющий видеть врага над стенами.^[7] Кавалерская перспектива - это то, как вещи были видны с этой высокой точки. Некоторые также объясняют это название тем, что всадник мог видеть небольшой объект на земле со своей лошади.^[8]

Проекция кабинета

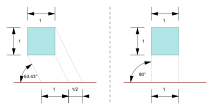
Период, термин проекция шкафа проистекает из его использования в иллюстрациях в мебельной промышленности.^[9] Как и в кавалерской перспективе, одна грань проецируемого объекта параллельна плоскости обзора, а третья ось проецируется как уходящая под углом (обычно атан (2) или около ~ 63,4 °). В отличие от кавалерийской проекции, где третья ось сохраняет свою длину, в корпусной проекции длина отступающих линий сокращается вдвое.

Математическая формула

Как формула, если самолет, обращенный к зрителю, ху, а удаляющаяся ось - z, затем точка п проектируется так:

${\displaystyle P{\begin{pmatrix}x\\y\\z\end{pmatrix}}={\begin{pmatrix}x+{\frac {1}{2}}z\cos \alpha \\y+{\frac {1}{2}}z\sin \alpha \\0\end{pmatrix}}}$

Где ${\displaystyle \alpha }$ - упомянутый угол.

В матрица преобразования является:

${\displaystyle P={\begin{bmatrix}1&0&{\frac {1}{2}}\cos \alpha \\0&1&{\frac {1}{2}}\sin \alpha \\0&0&0\end{bmatrix}}}$

В качестве альтернативы можно было бы удалить одну треть ведущего плеча, выступающего за стартовую поверхность, что даст тот же результат.

Военная проекция

в военная проекция, углы Икс и zось и у и z -оси находятся под углом 45 °, что означает, что угол между Иксось и у- ось 90 °. Это xz-самолет не перекошен. Однако он повернут более чем на 45 °.^[10]

Примеры

Помимо технических чертежей и иллюстраций, видеоигры (особенно те, которые предшествовали появлению 3D-игр) также часто используют форму наклонной проекции. Примеры включают SimCity, Ultima VII, Ultima Online, EarthBound, Разносчик газет и совсем недавно Большеберцовая кость.

• 

  Цифры слева орфографические проекции. Цифра справа - это косая проекция с углом 30 ° и соотношением¹⁄₂.

• 

  Скамья для горшков обращается в проекция шкафа с углом 45 ° и соотношением 2/3.

• 

  Части фортификации в бесцеремонная перспектива (Циклопедия т. 1, 1728).

• 

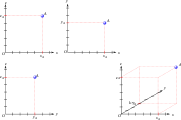
  Как координаты используются для размещения точки на бесцеремонная перспектива.

• 

  Каменная арка нарисована в военная перспектива.

• 

  Каменная арка нарисована в кабинетная перспектива.

• 

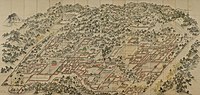
  Представитель Корейский картина с изображением двух королевских дворцов, Чхандоккун и Чхангёнгун расположен на востоке от главного дворца, Кёнбоккун.

• 

  Подъезд и двор яменя. Деталь прокрутки о Сучжоу Сюй Ян, заказанный Цяньлун Император. 18-ый век

• 

  План 18 века Port-Royal-des-Champs обращается в военная проекция

• 

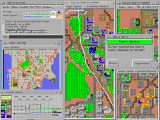
  Вариант военная проекция используется в видеоигре SimCity

• 

  А 3D визуализация магнитно-резонансная ангиография, показаны в косой проекции, чтобы различать аберрантная подключичная артерия

Смотрите также

• Космическая проекция Меркатора
• Косая проекция Меркатора
• Хацусабуро Ёсида
• Список художественных техник

Рекомендации

1. Кукер, Феликс (2013). Многообразные зеркала: пути пересечения искусства и математики. Издательство Кембриджского университета. С. 269–278. ISBN  978-0-521-72876-8.
2. Вайсштейн, Эрик В. «Теорема Польке». Материал из MathWorld - веб-ресурса Wolfram.
3. Параллельные проекции В архиве 23 апреля 2007 г. Wayback Machine из PlaneView3D онлайн
4. Болтон, Уильям (1995), Базовое проектирование, Butterworth-Heinemann GNVQ Engineering Series, BH Newnes, стр. 140, ISBN  9780750625845.
5. [«Руководства по ремонту и техническому обслуживанию - Комплексное издательство». Архивировано из оригинал 22 августа 2010 г.. Получено 22 августа 2010./content/draftsman/14276/css/14276_307.htm Illustrator Draftsman 3 и 2 - Volume 2 Standard Practices and Theory, page 67] из «Руководства по ремонту и техническому обслуживанию - Комплексное издательство». Архивировано из оригинал 22 августа 2010 г.. Получено 22 августа 2010.
6. Ингрид Карлбом, Джозеф Пасиорек, Плоские геометрические проекции и преобразования просмотра, Опросы ACM Computing, v.10, n.4, pp. 465–502, декабрь 1978 г.
7. Etymologie des maths, буква C (Французский)
8. DES QUESTIONS D'ORIGINES (Французский)
9. Чинг, Фрэнсис Д. К .; Юрошек, Стивен П. (2011), Чертеж дизайна (2-е изд.), John Wiley & Sons, стр. 205, ISBN  9781118007372.
10. «Геометрия перспективного рисования на компьютере». Получено 24 апреля 2015.

дальнейшее чтение

• Фоли, Джеймс (1997). Компьютерная графика. Бостон: Эддисон-Уэсли. ISBN  0-201-84840-6.
• Ингрид Карлбом, Джозеф Пасиорек, Плоские геометрические проекции и преобразования просмотра, Опросы ACM Computing, т.10, п.4, с. 465–502, декабрь 1978 г.
• Альфа и др. 1988 г., Атлас наклонных карт, сборник изображений рельефа избранных областей мира (Геологическая служба США )

внешняя ссылка

• Illustrator Draftsman 3 и 2 - Том 2 Стандартные практики и теория, стр. 68 из https://web.archive.org/web/20100822152816/http://www.tpub.com:80/