Четырехзвенная навеска - Four-bar linkage

А четырехзвенная навеска, также называемый четырехтактный, является простейшей подвижной замкнутой цепью связь. Он состоит из четырех корпусов, называемых стержнями или звеньями, соединенных в петлю четырьмя шарнирами. Обычно соединения имеют такую конфигурацию, что звенья движутся в параллельных плоскостях, и сборка называется планарная четырехзвенная навеска. Сферические и пространственные четырехзвенные связи также существуют и используются на практике.^[1]

Основным механизмом Pumpjacks является четырехзвенная навеска.

Планарная четырехзвенная навеска

Кривые сцепления четырехзвенного рычага кривошипно-коромысла. Моделирование выполнено с помощью MeKin2D.

Плоские четырехстоечные рычаги состоят из четырех звеньев, соединенных в петлю четырьмя одноручными.степень свободы суставы. Сустав может быть либо восставший, то есть шарнирное соединение, обозначенное R, или призматическое, как скользящее соединение, обозначенное P.

Линия, соединенная с землей шарнирным соединением, обычно называется заводить. Линия, соединенная с землей призматическим соединением, называется ползуном. Ползунки иногда считаются кривошипами, шарнир которых шарнирно расположен на очень большом расстоянии перпендикулярно движению ползуна.

Звено, соединяющее две кривошипы, называется плавающая ссылка или муфта. Муфта, соединяющая кривошип и ползун, часто называется шатун.

В зависимости от использования поворотных или призматических шарниров существует три основных типа планарной четырехзвенной связи:

Четыре поворотных сустава: планарная четырехугольная связь состоит из четырех звеньев и четырех вращательные суставы, обозначается RRRR. Он состоит из двух кривошипов, соединенных стяжкой.
Три шарнирных соединения и призматический шарнир: ползунок-кривошипно-рычажный механизм состоит из четырех звеньев, соединенных тремя поворотными и одним призматический шарнир, или RRRP. Он может быть сконструирован с кривошипом и ползунком, соединенным шатуном. Или он может быть сконструирован в виде двух кривошипов с ползунком, действующим как соединительный элемент, известный как перевернутый бегунок-кривошип.
Два шарнирных соединения и два призматических соединения: двойной слайдер это связь PRRP.^[2] Эта связь создается путем соединения двух ползунков с помощью соединительного звена. Если направления движения двух ползунов перпендикулярны, то траектории точек в соединителе являются эллипсами, а связь известна как эллиптический трамвай, или Барабан Архимеда.

Плоские четырехстоечные рычаги важны механизмы нашел в машины. В кинематика и динамика плоских четырехстержневых связей являются важными темами в машиностроение.

Планарные четырехстворчатые рычаги могут быть сконструированы для управления широким спектром движений.

Плоское четырехстороннее соединение

Плоские четырехсторонние рычаги, рычаги RRRR или 4R имеют четыре шарнирных соединения. Одно звено цепи обычно фиксируется и называется наземная связь, фиксированная ссылка, или Рамка. Две ссылки, подключенные к фрейму, называются обоснованные ссылки и обычно являются входными и выходными звеньями системы, иногда называемыми входная ссылка и выходная ссылка. Последняя ссылка - это плавающая ссылка, который также называют сцепка или шатун потому что он соединяет вход с выходом.

Предполагая, что фрейм расположен горизонтально, есть четыре возможности для входных и выходных ссылок:^[2]

Кривошип: может вращаться на 360 градусов
Коромысло: может вращаться в ограниченном диапазоне углов, не включая 0 ° или 180 °.
0-рокер: может вращаться в ограниченном диапазоне углов, который включает 0 °, но не 180 °.
Π-рокер: может вращаться в ограниченном диапазоне углов, который включает 180 °, но не 0 °

Некоторые авторы не различают типы рокеров.

Состояние Грасгофа

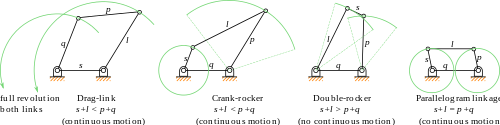
Условие Грасгофа для четырехзвенной связи гласит: Если сумма самого короткого и самого длинного звена плоского четырехугольного звена меньше или равна сумме двух оставшихся звеньев, то самое короткое звено может полностью вращаться относительно соседнего звена. Другими словами, условие выполняется, если S + L ≤ п + Q, где S это самая короткая ссылка, L самый длинный, и п и Q другие ссылки.

Классификация

Движение четырехстороннего рычага можно разделить на восемь случаев в зависимости от размеров его четырех звеньев. Пусть a, b, g и h обозначают длины входного кривошипа, выходного кривошипа, заземляющего звена и плавающего звена соответственно. Затем мы можем построить три члена:

{ displaystyle T_ {1} = g + h-a-b}

;

{ displaystyle T_ {2} = b + g-a-h}

;

{ displaystyle T_ {3} = b + h-a-g}

.

Движение четырехугольного рычага можно разделить на восемь типов на основе положительных и отрицательных значений этих трех элементов, T₁, Т₂, и т₃.^[2]

${ displaystyle T_ {1}}$	${ displaystyle T_ {2}}$	${ displaystyle T_ {3}}$	Состояние Грасгофа	Входная ссылка	Выходная ссылка
−	−	+	Grashof	Кривошип	Кривошип
+	+	+	Grashof	Кривошип	Рокер
+	−	−	Grashof	Рокер	Кривошип
−	+	−	Grashof	Рокер	Рокер
−	−	−	Non-Grashof	0-рокер	0-рокер
−	+	+	Non-Grashof	π-рокер	π-рокер
+	−	+	Non-Grashof	π-рокер	0-рокер
+	+	−	Non-Grashof	0-рокер	π-рокер

Случаи T₁ = 0, T₂ = 0 и T₃ = 0 интересны, потому что связи сворачиваются. Если выделить складывающуюся четырехугольную навеску, то существует 27 различных случаев.

На рисунке показаны примеры различных случаев плоского четырехугольного рычажного механизма.^[3]

Типы четырехзвенных рычагов, s: кратчайшая ссылка, л: самая длинная ссылка.

Конфигурацию четырехугольного рычага можно разделить на три типа: выпуклый, вогнутый и перекрестный. В выпуклом и вогнутом случаях никакие два звена не пересекаются друг с другом. В перекрестном соединении два звена пересекаются друг с другом. В выпуклом случае все четыре внутренних угла меньше 180 градусов, а в вогнутой конфигурации один внутренний угол больше 180 градусов. Существует простое геометрическое соотношение между длинами двух диагоналей четырехугольника. Для выпуклых и перекрестных связей длина одной диагонали увеличивается тогда и только тогда, когда другая уменьшается. С другой стороны, для невыпуклых непересекающихся связей все обстоит наоборот; одна диагональ увеличивается тогда и только тогда, когда другая также увеличивается.^[4]

Конструкция четырехзвенных механизмов

Синтез или дизайн четырехбалочного механизмы важен при стремлении произвести желаемое выходное движение для определенного входного движения. Чтобы свести к минимуму стоимость и максимизировать эффективность, проектировщик выберет самый простой из возможных механизмов для выполнения желаемого движения. При выборе типа механизма, который будет спроектирован, длины звеньев должны определяться с помощью процесса, называемого размерным синтезом. Размерный синтез включает повторять и анализировать методология, которая в определенных обстоятельствах может оказаться неэффективным процессом; однако в уникальных сценариях точные и подробные процедуры для разработки точного механизма могут не существовать.^[5]

Соотношение времени

Соотношение времени (Q) четырехзвенного механизма является мерой его быстрого возврата и определяется следующим образом:^[5]

{ displaystyle Q = { frac { text {Время более медленного хода}} { text {Время более быстрого хода}}} geq 1}

При четырехстержневых механизмах имеется два удары, форвард и возврат, которые при сложении образуют цикл. Каждый ход может быть идентичным или иметь разную среднюю скорость. Отношение времени численно определяет, насколько быстро прямой ход по сравнению с более быстрым обратным ходом. Общее время цикла ( $Δt цикл$ ) для механизма:^[5]

{ displaystyle Delta t _ { text {cycle}} = { text {Время более медленного хода}} + { text {Время более быстрого хода}}}

Большинство механизмов с четырьмя стержнями приводится в действие приводом вращения или кривошипом, для которого требуется определенная постоянная скорость. Эта требуемая скорость (ω_{заводить}) связана со временем цикла следующим образом:^[5]

{ displaystyle omega _ { text {кривошип}} = ( Delta t _ { text {cycle}}) ^ {- 1}}

Некоторые механизмы, производящие возвратно-поступательное или повторяющееся движение, предназначены для создания симметричного движения. То есть, ход машины вперед движется с той же скоростью, что и обратный ход. Эти механизмы, которые часто называют в соответствии конструкции, обычно работают в обоих направлениях, так как они оказывают одинаковую силу в обоих направлениях.^[5]

Примеры механизмов симметричного движения включают:

Дворники
Механизмы двигателя или поршни
Шатуны окна автомобиля

Для других приложений требуется, чтобы проектируемый механизм имел более высокую среднюю скорость в одном направлении, чем в другом. Эта категория механизмов наиболее желательна для проектирования, когда требуется работа только в одном направлении. Скорость, с которой работает этот один ход, также очень важна для определенных машин. Как правило, возвратный и неинтенсивный гребок должен выполняться как можно быстрее. Таким образом, большая часть времени в каждом цикле отводится на интенсивный гребок. Эти быстрое возвращение механизмы часто называют компенсировать.^[5]

Примеры механизмов компенсации включают:

Станки для резки
Устройства для перемещения пакетов

При использовании механизмов смещения очень важно понимать, как и в какой степени смещение влияет на соотношение времени. Чтобы связать геометрию конкретной связи с синхронизацией хода, угол дисбаланса (β) используется. Этот угол связан с соотношением времени, Q, следующее:^[5]

{ displaystyle Q = { frac {180 ^ { circ} + beta} {180 ^ { circ} - beta}}}

Путем простой алгебраической перестановки это уравнение можно переписать так, чтобы оно решало для β:^[5]

{ displaystyle beta = 180 ^ { circ} times { frac {Q-1} {Q + 1}}}

Временные диаграммы

Временные диаграммы часто используются для синхронизации движение между двумя или более механизмами. Они графически отображают информацию, показывающую, где и когда каждый механизм неподвижен или выполняет свои прямые и обратные ходы. Временные диаграммы позволяют дизайнерам качественно описать необходимые кинематический поведение механизма.^[5]

Эти графики также используются для оценки скоростей и ускорений определенных четырехзвенников. Скорость ссылки - это временная скорость, с которой его позиция изменяется, а ускорение ссылки - это временная скорость, с которой изменяется его скорость. И скорость, и ускорение вектор количествах, в которых оба величина и направление; однако в временных диаграммах используются только их величины. При использовании с двумя механизмами временные диаграммы предполагают постоянное ускорение. Это предположение дает полиномиальные уравнения для скорости как функции времени. Постоянное ускорение позволяет отображать график зависимости скорости от времени в виде прямых линий, тем самым определяя взаимосвязь между смещение (ΔR), максимальная скорость (v_{вершина горы}), ускорение (а), и время(Δt). Следующие уравнения показывают это.^[5]^[6]

Δ р = 1 / 2 v вершина горы Δ т

Δ р = 1 / 4 а (Δ т) 2

Учитывая смещение и время, можно вычислить максимальную скорость и ускорение каждого механизма в данной паре.^[5]

Ползунок-кривошипно-рычажный механизм

Кривошипно-ползунковые механизмы с эксцентриситетом 0 и 1,25.

Кривошипно-ползунковая связь представляет собой четырехзвенную связь с тремя поворотными шарнирами и одним призматическим или скользящим шарниром. Вращение заводить приводит в движение линейное движение ползунка или расширение газов против скольжения поршень в цилиндре может управлять вращением кривошипа.

Есть два типа кривошипов: рядные и офсетные.

В соответствии: В линейном кривошипе ползунка ползунок расположен так, что линия движения шарнирного соединения ползуна проходит через базовое соединение кривошипа. Это создает симметричное движение ползунка вперед и назад при вращении кривошипа.
Компенсировать: Если линия хода шарнирного соединения ползуна не проходит через базовый шарнир кривошипа, движение ползуна не симметрично. Он движется в одном направлении быстрее, чем в другом. Это называется механизм быстрого возврата.

Сферические и пространственные четырехзвенные рычаги

Если рычажный механизм имеет четыре шарнирных соединения с осями, расположенными под углом для пересечения в одной точке, то звенья перемещаются по концентрическим сферам, и сборка называется сферическая четырехзвенная навеска. Уравнения ввода-вывода сферической четырехзвенной связи могут быть применены к пространственным четырехзвенным связям, когда переменные заменены на двойные числа.^[7]

Связь Беннета представляет собой пространственный четырехзвенный рычажный механизм с шарнирными соединениями, оси которых наклонены определенным образом, что делает систему подвижной.^[8]^[2]

Универсальный шарнир.
Рулевое управление трактора
Четырехрычажная навеска Bennett.

Примеры

Биологические связи
Велосипедная подвеска
Доводчик
Пантограф (четыре такта, два степени свободы, т.е. фиксируется только одно шарнирное соединение.)
Pumpjack
Подвеска на двойных поперечных рычагах
Машины с ножным приводом, т.е. педаль швейная машина, точильный камень, токарный станок и т.п.
Планер (мебель)
Складные ступеньки и складные стулья
Шаг на мусорное ведро
Тяги переключения передач
Паровозы и локомотивы
Качающийся вентилятор
Связь Ватта и Чебышевская связь (рычаги, приближенные к прямолинейному движению)
Стеклоочиститель

Примеры моделирования

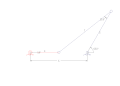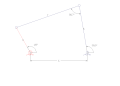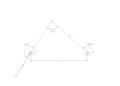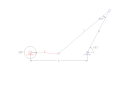
Кривошипно-коромысло останавливается в крайних положениях и при мин. / Макс. Угле передачи
Фиксированные и подвижные центроды четырехстержневой
Родственные муфты кривошипно-коромысла четырехтактный
рулевая тяга четырехрычажного типа (Акермана)
Генератор функций с четырьмя стержнями
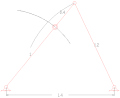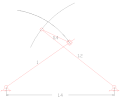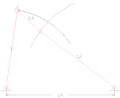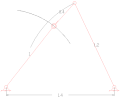
Поворотная муфта четырехзвенная навеска
Параллельные четырехзвенные рычаги
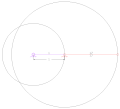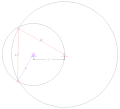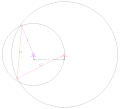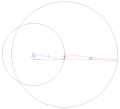
Галлоуэй (дельтовидная или кайт) четырехрычажная связь
Складной четырехзвенный рычажный механизм кривошипно-коромысла

Смотрите также

использованная литература

^ Хартенберг, Р. И Дж. Денавит (1964) Кинематический синтез связей, Нью-Йорк: McGraw-Hill, онлайн-ссылка Корнелл Университет.
^ ^а ^б ^c ^d Дж. М. Маккарти и Г. С. Со, Геометрический дизайн связей, 2-е издание, Springer, 2010 г.
^ Дизайн машин 3 / е, Роберт Л. Нортон, 2 мая 2003 г., МакГроу Хилл. ISBN 0-07-247046-1
^ Туссен, Г. Т., "Простые доказательства геометрического свойства четырехзвенных зацеплений", Американский математический ежемесячный журнал, Июнь – июль 2003 г., стр. 482–494.
^ ^а ^б ^c ^d ^е ^ж ^грамм ^час ^я ^j ^k Мышка, Дэвид (2012). Машины и механизмы: прикладной кинематический анализ. Нью-Джерси: образование Пирсона. ISBN 978-0-13-215780-3.
^ Чакрабарти, Амареш (2002). Синтез инженерного дизайна: понимание, подходы и инструменты. Великобритания: Springer-Verlag London Limited. ISBN 978-1852334925.
^ Анхелес, Хорхе (2012), "Двойные обобщенные инверсии и их приложения в кинематическом синтезе", Последние достижения в кинематике роботов, Springer, Нидерланды, стр. 1–10, Дои:10.1007/978-94-007-4620-6_1, ISBN 9789400746190
^ Хант, К. Х., Кинематическая геометрия механизмов, Oxford Engineering Science Series, 1979.

внешние ссылки

Четырех стержневые связи в коллекции моделей Reuleaux в Корнельском университете

[1] Хартенберг, Р. И Дж. Денавит (1964) Кинематический синтез связей, Нью-Йорк: McGraw-Hill, онлайн-ссылка Корнелл Университет.

[McCarthy-2] а ^б ^c ^d Дж. М. Маккарти и Г. С. Со, Геометрический дизайн связей, 2-е издание, Springer, 2010 г.

[3] Дизайн машин 3 / е, Роберт Л. Нортон, 2 мая 2003 г., МакГроу Хилл. ISBN 0-07-247046-1

[4] Туссен, Г. Т., "Простые доказательства геометрического свойства четырехзвенных зацеплений", Американский математический ежемесячный журнал, Июнь – июль 2003 г., стр. 482–494.

[Myszka-5] а ^б ^c ^d ^е ^ж ^грамм ^час ^я ^j ^k Мышка, Дэвид (2012). Машины и механизмы: прикладной кинематический анализ. Нью-Джерси: образование Пирсона. ISBN 978-0-13-215780-3.

[Chak-6] Чакрабарти, Амареш (2002). Синтез инженерного дизайна: понимание, подходы и инструменты. Великобритания: Springer-Verlag London Limited. ISBN 978-1852334925.

[7] Анхелес, Хорхе (2012), "Двойные обобщенные инверсии и их приложения в кинематическом синтезе", Последние достижения в кинематике роботов, Springer, Нидерланды, стр. 1–10, Дои:10.1007/978-94-007-4620-6_1, ISBN 9789400746190

[8] Хант, К. Х., Кинематическая геометрия механизмов, Oxford Engineering Science Series, 1979.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]