Выбор функции - Feature selection
Эта статья включает в себя список общих Рекомендации, но он остается в основном непроверенным, потому что ему не хватает соответствующих встроенные цитаты. (Июль 2010 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
| Часть серии по |
| Машинное обучение и сбор данных |
|---|
Площадки для машинного обучения |
В машинное обучение и статистика, выбор функции, также известный как выбор переменных, выбор атрибута или же выбор подмножества переменных, это процесс выбора подмножества соответствующих Особенности (переменные, предикторы) для использования при построении модели. Методы выбора характеристик используются по нескольким причинам:
- упрощение моделей для облегчения их интерпретации исследователями / пользователями,[1]
- более короткое время обучения,
- чтобы избежать проклятие размерности,
- усиление обобщения за счет сокращения переоснащение[2] (формально сокращение отклонение[1])
Центральная предпосылка при использовании метода выбора признаков заключается в том, что данные содержат некоторые особенности, которые либо избыточный или же не имеющий отношения, и поэтому его можно удалить без большой потери информации.[2] Избыточный и не имеющий отношения - это два разных понятия, поскольку одна релевантная функция может быть избыточной при наличии другой соответствующей функции, с которой она сильно коррелирует.[3]
Методы выбора характеристик следует отличать от извлечение признаков.[4] Извлечение функций создает новые функции из функций исходных функций, тогда как выбор функции возвращает подмножество функций. Методы выбора характеристик часто используются в областях, где есть много функций и сравнительно мало образцов (или точек данных). Типичные случаи применения выбора признаков включают анализ письменные тексты и Микрочип ДНК data, где есть многие тысячи функций и от нескольких десятков до сотен образцов.
Вступление
Алгоритм выбора признаков можно рассматривать как комбинацию метода поиска для предложения новых подмножеств признаков вместе с мерой оценки, которая оценивает различные подмножества признаков. Самый простой алгоритм - проверить каждое возможное подмножество функций, найти ту, которая минимизирует частоту ошибок. Это исчерпывающий поиск в пространстве, который с вычислительной точки зрения не поддается обработке для всех наборов функций, кроме самых маленьких. Выбор метрики оценки сильно влияет на алгоритм, и именно эти метрики оценки различают три основные категории алгоритмов выбора функций: оболочки, фильтры и встроенные методы.[3]
- В методах оболочки используется прогнозная модель для оценки подмножеств функций. Каждое новое подмножество используется для обучения модели, которая тестируется на удерживающем наборе. Подсчет количества ошибок, сделанных на этом удерживающем наборе (коэффициент ошибок модели), дает оценку для этого подмножества. Поскольку методы оболочки обучают новую модель для каждого подмножества, они требуют больших вычислительных ресурсов, но обычно обеспечивают наиболее эффективный набор функций для этого конкретного типа модели или типичной проблемы.
- Методы фильтрации используют прокси-меру вместо частоты ошибок для оценки подмножества функций. Эта мера выбрана так, чтобы ее можно было быстро вычислить, при этом сохраняя полезность набора функций. Общие меры включают взаимная информация,[3] в точечная взаимная информация,[5] Коэффициент корреляции продукт-момент Пирсона, Алгоритмы на основе рельефа,[6] и меж / внутриклассное расстояние или баллы тесты значимости для каждой комбинации класса / функции.[5][7] Фильтры обычно менее требовательны к вычислениям, чем оболочки, но они создают набор функций, который не настроен на конкретный тип прогнозной модели.[8] Это отсутствие настройки означает, что набор функций из фильтра является более общим, чем набор из оболочки, и обычно дает более низкую производительность прогнозирования, чем оболочка. Однако набор функций не содержит допущений модели прогнозирования и поэтому более полезен для выявления взаимосвязей между функциями. Многие фильтры предоставляют ранжирование функций, а не явное подмножество лучших функций, и точка отсечения в ранжировании выбирается через перекрестная проверка. Методы фильтрации также использовались в качестве этапа предварительной обработки для методов оболочки, позволяя использовать оболочку для более крупных проблем. Еще один популярный подход - алгоритм исключения рекурсивных признаков,[9] обычно используется с Машины опорных векторов для многократного построения модели и удаления элементов с малым весом.
- Встроенные методы - это комплексная группа методов, которые выполняют выбор функций как часть процесса построения модели. Примером такого подхода является ЛАССО метод построения линейной модели, который штрафует коэффициенты регрессии штрафом L1, уменьшая многие из них до нуля. Любые функции, имеющие ненулевые коэффициенты регрессии, «выбираются» алгоритмом LASSO. Улучшения LASSO включают Bolasso, который загружает сэмплы;[10] Упругая сетевая регуляризация, который комбинирует штраф L1 LASSO со штрафом L2 регресс гребня; и FeaLect, который оценивает все функции на основе комбинаторного анализа коэффициентов регрессии.[11] AEFS расширяет LASSO до нелинейных сценариев с автокодировщиками.[12] Эти подходы, как правило, находятся между фильтрами и оболочками с точки зрения вычислительной сложности.
В традиционных регрессивный анализ, наиболее популярной формой выбора функций является пошаговая регрессия, который является техникой обертки. Это жадный алгоритм который добавляет лучшую характеристику (или удаляет худшую характеристику) в каждом раунде. Основная проблема контроля - решить, когда остановить алгоритм. В машинном обучении это обычно делается перекрестная проверка. В статистике оптимизированы некоторые критерии. Это приводит к внутренней проблеме вложенности. Были изучены более надежные методы, такие как ветвь и переплет и кусочно-линейная сеть.
Выбор подмножества
Выбор подмножества оценивает пригодность подмножества функций как группы. Алгоритмы выбора подмножества можно разбить на оболочки, фильтры и встроенные методы. Обертки используют алгоритм поиска для поиска в пространстве возможных функций и оценки каждого подмножества путем запуска модели на подмножестве. Обертки могут быть дорогостоящими в вычислительном отношении и иметь риск излишнего соответствия модели. Фильтры аналогичны оболочкам в подходе поиска, но вместо оценки по модели оценивается более простой фильтр. Встроенные методы встроены в модель и относятся к ней.
Многие популярные методы поиска используют жадный скалолазание, который итеративно оценивает подмножество функций-кандидатов, затем изменяет подмножество и оценивает, является ли новое подмножество улучшением по сравнению со старым. Оценка подмножеств требует выставления баллов метрика который оценивает подмножество функций. Исчерпывающий поиск обычно непрактичен, поэтому в точке остановки, определенной разработчиком (или оператором), в качестве удовлетворительного подмножества функций выбирается подмножество функций с наивысшей оценкой, обнаруженной до этой точки. Критерий остановки зависит от алгоритма; Возможные критерии включают: оценка подмножества превышает пороговое значение, превышено максимально допустимое время выполнения программы и т. д.
Альтернативные методы поиска основаны на преследование целевой проекции которая находит низкоразмерные проекции данных с высокими оценками: затем выбираются объекты с наибольшими проекциями в низкоразмерном пространстве.
Подходы к поиску включают:
- Исчерпывающий[13]
- Лучшие сначала
- Имитация отжига
- Генетический алгоритм[14]
- Жадный прямой выбор[15][16][17]
- Жадное обратное устранение
- Оптимизация роя частиц[18]
- Целенаправленное преследование проекции
- Scatter search[19]
- Поиск переменного района[20][21]
Две популярные метрики фильтра для задач классификации: корреляция и взаимная информация, хотя ни то, ни другое не соответствует действительности метрики или "меры расстояния" в математическом смысле, поскольку они не подчиняются неравенство треугольника и, таким образом, не вычисляют никакого фактического «расстояния» - их скорее следует рассматривать как «баллы». Эти баллы вычисляются между функцией-кандидатом (или набором функций) и желаемой выходной категорией. Однако есть настоящие метрики, которые являются простой функцией взаимной информации;[22] видеть Вот.
Другие доступные показатели фильтра включают:
- Разделимость классов
- Вероятность ошибки
- Межклассовое расстояние
- Вероятностное расстояние
- Энтропия
- Выбор функций на основе согласованности
- Выбор признаков на основе корреляции
Критерии оптимальности
Выбор критериев оптимальности затруднен, поскольку задача выбора характеристик преследует несколько целей. Многие общие критерии включают меру точности, за которую накладывается количество выбранных функций. Примеры включают Информационный критерий Акаике (AIC) и Mallows's Cп, которые имеют штраф 2 за каждую добавленную функцию. АПК основан на теория информации, и эффективно выводится через принцип максимальной энтропии.[23][24]
Другие критерии Байесовский информационный критерий (BIC), в котором применяется штраф в размере для каждой добавленной функции, минимальная длина описания (MDL), который асимптотически использует , Бонферрони / RIC, которые используют , максимальный выбор функций зависимости и множество новых критериев, которые мотивированы коэффициент ложного обнаружения (FDR), которые используют что-то близкое к . Максимум скорость энтропии критерий также может использоваться для выбора наиболее подходящего подмножества функций.[25]
Структурное обучение
Выбор функции фильтра - это частный случай более общей парадигмы, называемой структурное обучение. Выбор функций находит соответствующий набор функций для конкретной целевой переменной, тогда как структурное обучение находит взаимосвязи между всеми переменными, обычно выражая эти отношения в виде графика. Наиболее распространенные алгоритмы изучения структуры предполагают, что данные генерируются Байесовская сеть, поэтому структура представляет собой направленный графическая модель. Оптимальным решением проблемы выбора функции фильтра является Марковское одеяло целевого узла, а в байесовской сети существует уникальное марковское одеяло для каждого узла.[26]
Механизмы выбора характеристик, основанные на теории информации
Существуют различные механизмы выбора функций, которые используют взаимная информация для оценки различных функций. Обычно они используют один и тот же алгоритм:
- Рассчитайте взаимная информация как оценка между всеми функциями () и целевой класс ()
- Выберите функцию с наибольшим количеством баллов (например, ) и добавить его в набор выбранных функций ()
- Рассчитайте балл, который может быть получен из взаимная информация
- Выберите функцию с наибольшей оценкой и добавьте ее в набор выбранных функций (например, )
- Повторяйте 3. и 4., пока не будет выбрано определенное количество функций (например, )
Самый простой подход использует взаимная информация как «производная» оценка.[27]
Однако есть разные подходы, которые пытаются уменьшить избыточность между функциями.
Выбор функции минимальной избыточности и максимальной релевантности (mRMR)
Пэн и другие.[28] предложила метод выбора признаков, который может использовать либо взаимную информацию, корреляцию, либо оценки расстояния / сходства для выбора объектов. Цель состоит в том, чтобы снизить актуальность функции из-за ее избыточности в присутствии других выбранных функций. Актуальность набора функций S для класса c определяется средним значением всех значений взаимной информации между индивидуальным признаком жя и класс c следующее:
- .
Резервирование всех функций в наборе S среднее значение всех значений взаимной информации между функцией жя и особенность жj:
Критерий mRMR представляет собой комбинацию двух приведенных выше показателей и определяется следующим образом:
Предположим, что есть п полный набор функций. Позволять Икся быть установленным членством индикаторная функция для функции жя, так что Икся=1 указывает на присутствие и Икся=0 указывает на отсутствие функции жя в глобально оптимальном наборе функций. Позволять и . Вышеизложенное можно затем записать как задачу оптимизации:
Алгоритм mRMR - это приближение теоретически оптимального алгоритма выбора признаков с максимальной зависимостью, который максимизирует взаимную информацию между совместным распределением выбранных признаков и переменной классификации. Поскольку mRMR аппроксимирует комбинаторную задачу оценивания серией гораздо меньших задач, каждая из которых включает только две переменные, она, таким образом, использует более надежные попарные совместные вероятности. В определенных ситуациях алгоритм может недооценивать полезность функций, поскольку у него нет способа измерить взаимодействия между функциями, которые могут повысить релевантность. Это может привести к снижению производительности[27] когда функции по отдельности бесполезны, но полезны в сочетании (патологический случай обнаруживается, когда класс функция четности функций). В целом алгоритм более эффективен (с точки зрения объема требуемых данных), чем теоретически оптимальный выбор максимальной зависимости, но при этом создает набор функций с небольшой попарной избыточностью.
mRMR - это пример большого класса методов фильтрации, которые по-разному балансируют между релевантностью и избыточностью.[27][29]
Выбор функции квадратичного программирования
mRMR является типичным примером инкрементной жадной стратегии для выбора функции: после того, как функция была выбрана, ее нельзя отменить на более позднем этапе. Хотя mRMR можно оптимизировать с помощью плавающего поиска для уменьшения некоторых функций, его также можно переформулировать как глобальный квадратичное программирование Задача оптимизации следующая:[30]
куда вектор релевантности функции при наличии п всего функций, - матрица попарной избыточности признаков, а представляет относительные веса функций. QPFS решается с помощью квадратичного программирования. Недавно было показано, что QFPS смещается в сторону функций с меньшей энтропией,[31] из-за размещения признака саморезервирования по диагонали ЧАС.
Условная взаимная информация
Другая оценка, полученная для взаимной информации, основана на условной релевантности:[31]
куда и .
Преимущество SPECCMI состоит в том, что ее можно решить, просто найдя доминирующий собственный вектор Q, таким образом, очень масштабируемый. SPECCMI также обрабатывает взаимодействие функций второго порядка.
Совместная взаимная информация
В исследовании с разными оценками Brown et al.[27] рекомендовал совместная взаимная информация[32] как хороший балл за выбор функций. Оценка пытается найти функцию, которая добавляет самую новую информацию к уже выбранным функциям, чтобы избежать дублирования. Оценка формулируется следующим образом:
В счете используется условная взаимная информация и взаимная информация для оценки избыточности между уже выбранными функциями () и исследуемый объект ().
Критерий независимости Гильберта-Шмидта Выбор функций на основе лассо
Для данных большой размерности и небольшой выборки (например, размерность> 105 и количество образцов <103), полезен критерий независимости Гильберта-Шмидта Лассо (HSIC Lasso).[33] Задача оптимизации HSIC Lasso задается как
куда - основанная на ядре мера независимости, называемая (эмпирическим) критерием независимости Гильберта-Шмидта (HSIC), обозначает след, - параметр регуляризации, и сосредоточены на входе и выходе Матрицы Грама, и - матрицы Грама, и - функции ядра, - центрирующая матрица, это м-размерный единичная матрица (м: количество образцов), это м-мерный вектор со всеми единицами, и это -норма. HSIC всегда принимает неотрицательное значение и равен нулю тогда и только тогда, когда две случайные величины статистически независимы, когда используется универсальное воспроизводящее ядро, такое как ядро Гаусса.
HSIC Lasso можно записать как
куда это Норма Фробениуса. Задача оптимизации - это проблема лассо, и поэтому ее можно эффективно решить с помощью современного решателя лассо, такого как двойная расширенный лагранжев метод.
Выбор корреляционной характеристики
Мера выбора признаков корреляции (CFS) оценивает подмножества признаков на основе следующей гипотезы: «Хорошие подмножества признаков содержат признаки, сильно коррелированные с классификацией, но не коррелированные друг с другом».[34][35] Следующее уравнение показывает достоинства подмножества функций S состоящий из k Функции:
Здесь, - среднее значение всех корреляций классификации признаков, и - среднее значение всех корреляций между характеристиками. Критерий CFS определяется следующим образом:
В и переменные называются корреляциями, но не обязательно Коэффициент корреляции Пирсона или же Спирмена ρ. В диссертации Холла не используется ни один из них, но используются три различных меры родства: минимальная длина описания (Лей), симметричная неопределенность, и облегчение.
Позволять Икся быть установленным членством индикаторная функция для функции жя; то приведенное выше можно переписать как задачу оптимизации:
Комбинаторные задачи, приведенные выше, на самом деле являются смешанными 0–1 линейное программирование проблемы, которые можно решить с помощью алгоритмы ветвей и границ.[36]
Регуляризованные деревья
Особенности из Древо решений или дерево ансамбль показаны как избыточные. Недавний метод, называемый регуляризованным деревом[37] может использоваться для выбора подмножества функций. Регуляризованные деревья наказываются использованием переменной, аналогичной переменным, выбранным в предыдущих узлах дерева для разделения текущего узла. Регуляризованные деревья нуждаются в построении только одной модели дерева (или одной модели ансамбля деревьев) и, следовательно, являются эффективными с вычислительной точки зрения.
Регуляризованные деревья естественным образом обрабатывают числовые и категориальные особенности, взаимодействия и нелинейности. Они инвариантны к шкалам атрибутов (единицам) и нечувствительны к выбросы, и, следовательно, не требуют предварительной обработки данных, например нормализация. Регуляризованный случайный лес (RRF)[38] - это один из типов регуляризованных деревьев. Управляемый RRF - это улучшенный RRF, который руководствуется оценками важности из обычного случайного леса.
Обзор методов метаэвристики
А метаэвристический это общее описание алгоритма, предназначенного для решения сложных (обычно NP-жесткий проблема) задачи оптимизации, для которых нет классических методов решения. Обычно метаэвристика - это стохастический алгоритм, стремящийся достичь глобального оптимума. Существует множество метаэвристик, от простого локального поиска до сложного глобального алгоритма поиска.
Основные принципы
Методы выбора функций обычно представлены в трех классах в зависимости от того, как они сочетают алгоритм выбора и построение модели.
Метод фильтрации
Методы типа фильтра выбирают переменные независимо от модели. Они основаны только на общих характеристиках, таких как корреляция с прогнозируемой переменной. Методы фильтрации подавляют наименее интересные переменные. Другие переменные будут частью классификации или регрессионной модели, используемой для классификации или прогнозирования данных. Эти методы особенно эффективны с точки зрения времени вычислений и устойчивы к переобучению.[39]
Методы фильтрации, как правило, выбирают избыточные переменные, когда они не учитывают взаимосвязи между переменными. Однако более сложные функции пытаются минимизировать эту проблему, удаляя переменные, сильно коррелированные друг с другом, такие как алгоритм FCBF.[40]
Метод обертки
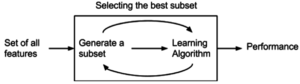
Методы оболочки оценивают подмножества переменных, что позволяет, в отличие от подходов к фильтрам, обнаруживать возможные взаимодействия между переменными.[41] Два основных недостатка этих методов:
- Возрастающий риск переобучения при недостаточном количестве наблюдений.
- Значительное время вычислений при большом количестве переменных.
Встроенный метод
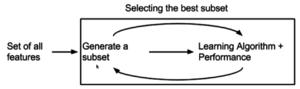
Недавно были предложены встроенные методы, которые пытаются объединить преимущества обоих предыдущих методов. Алгоритм обучения использует свой собственный процесс выбора переменных и одновременно выполняет выбор и классификацию признаков, например алгоритм FRMT.[42]
Применение метаэвристики выбора признаков
Это обзор применения метаэвристики выбора признаков, используемой в последнее время в литературе. Этот обзор был проведен Дж. Хэммон в своей диссертации 2013 года.[39]
| Заявление | Алгоритм | Подход | Классификатор | Функция оценки | Ссылка |
|---|---|---|---|---|---|
| SNP | Выбор функций с использованием сходства функций | Фильтр | р2 | Phuong 2005[41] | |
| SNP | Генетический алгоритм | Обертка | Древо решений | Точность классификации (10 раз) | Шах 2004[43] |
| SNP | скалолазание | Фильтр + Обертка | Наивный байесовский | Прогнозируемая остаточная сумма квадратов | Длинный 2007[44] |
| SNP | Имитация отжига | Наивный байесовский | Точность классификации (5-кратная) | Устункар 2011[45] | |
| Сегменты условно-досрочное освобождение | Колония муравьев | Обертка | Искусственная нейронная сеть | MSE | Аль-Ани 2005[нужна цитата ] |
| Маркетинг | Имитация отжига | Обертка | Регресс | AIC, р2 | Мейри 2006[46] |
| Экономика | Имитация отжига, генетический алгоритм | Обертка | Регресс | BIC | Капетаниос 2007[47] |
| Спектральная масса | Генетический алгоритм | Обертка | Множественная линейная регрессия, Частичные наименьшие квадраты | Средняя квадратическая ошибка предсказания | Broadhurst et al. 1997 г.[48] |
| Спам | Бинарный PSO + Мутация | Обертка | Древо решений | взвешенная стоимость | Чжан 2014[18] |
| Микрочип | Табу поиск + PSO | Обертка | Машина опорных векторов, K Ближайшие соседи | Евклидово расстояние | Чуанг 2009[49] |
| Микрочип | PSO + Генетический алгоритм | Обертка | Машина опорных векторов | Точность классификации (10 раз) | Альба 2007[50] |
| Микрочип | Генетический алгоритм + Итерированный локальный поиск | Встроенный | Машина опорных векторов | Точность классификации (10 раз) | Дюваль 2009[51] |
| Микрочип | Повторный локальный поиск | Обертка | Регресс | Апостериорная вероятность | Ганс 2007[52] |
| Микрочип | Генетический алгоритм | Обертка | K Ближайшие соседи | Точность классификации (Перекрестная проверка без исключения ) | Джирапеч-Умпай 2005[53] |
| Микрочип | Гибридный генетический алгоритм | Обертка | K Ближайшие соседи | Точность классификации (перекрестная проверка без исключения) | О 2004[54] |
| Микрочип | Генетический алгоритм | Обертка | Машина опорных векторов | Чувствительность и специфичность | Сюань 2011[55] |
| Микрочип | Генетический алгоритм | Обертка | Все парные машины опорных векторов | Точность классификации (перекрестная проверка без исключения) | Пэн 2003[56] |
| Микрочип | Генетический алгоритм | Встроенный | Машина опорных векторов | Точность классификации (10 раз) | Эрнандес 2007[57] |
| Микрочип | Генетический алгоритм | Гибридный | Машина опорных векторов | Точность классификации (перекрестная проверка без исключения) | Huerta 2006[58] |
| Микрочип | Генетический алгоритм | Машина опорных векторов | Точность классификации (10 раз) | Муни 2006[59] | |
| Микрочип | Генетический алгоритм | Обертка | Машина опорных векторов | EH-DIALL, CLUMP | Журдан 2005[60] |
| Болезнь Альцгеймера | T-критерий Велча | Фильтр | Машина опорных векторов | Точность классификации (10 раз) | Чжан 2015[61] |
| Компьютерное зрение | Бесконечный выбор функций | Фильтр | Независимый | Средняя точность, ROC AUC | Roffo 2015[62] |
| Микрочипы | Центральность собственного вектора FS | Фильтр | Независимый | Средняя точность, точность, ROC AUC | Роффо и Мельци 2016[63] |
| XML | Симметричный тау (ST) | Фильтр | Структурно-ассоциативная классификация | Точность, охват | Шахарани и Хаджич 2014 |
Выбор функций встроен в алгоритмы обучения
Некоторые алгоритмы обучения выполняют выбор функций как часть своей общей работы. К ним относятся:
- -техники регуляризации, такие как разреженная регрессия, LASSO и -SVM
- Регуляризованные деревья,[37] например регуляризованный случайный лес, реализованный в пакете RRF[38]
- Древо решений[64]
- Меметический алгоритм
- Случайный полиномиальный логит (RMNL)
- Авто-кодирование сети с узким местом
- Субмодульный выбор функции[65][66][67]
- Выбор функций на основе местного обучения.[68] По сравнению с традиционными методами, он не требует эвристического поиска, может легко обрабатывать многоклассовые задачи и работает как для линейных, так и для нелинейных задач. Он также поддерживается прочной теоретической базой. Численные эксперименты показали, что с помощью этого метода можно достичь решения, близкого к оптимальному, даже если данные содержат> 1 млн нерелевантных функций.
- Система рекомендаций, основанная на выборе функций.[69] Методы выбора характеристик вводятся в исследование рекомендательной системы.
Смотрите также
- Кластерный анализ
- Сбор данных
- Снижение размерности
- Извлечение признаков
- Оптимизация гиперпараметров
- Выбор модели
- Рельеф (выбор функции)
Рекомендации
- ^ а б Гарет Джеймс; Даниэла Виттен; Тревор Хасти; Роберт Тибширани (2013). Введение в статистическое обучение. Springer. п. 204.
- ^ а б Bermingham, Mairead L .; Понг-Вонг, Рикардо; Спилиопулу, Афина; Хейворд, Кэролайн; Рудан, Игорь; Кэмпбелл, Гарри; Райт, Алан Ф .; Уилсон, Джеймс Ф .; Агаков, Феликс; Наварро, По; Хейли, Крис С. (2015). «Применение многомерного отбора признаков: оценка для геномного прогнозирования у человека». Sci. Rep. 5: 10312. Bibcode:2015НатСР ... 510312Б. Дои:10.1038 / srep10312. ЧВК 4437376. PMID 25988841.
- ^ а б c Гийон, Изабель; Элиссефф, Андре (2003). «Введение в выбор переменных и функций». JMLR. 3.
- ^ Саранги, Сусанта; Сахидулла, штат Мэриленд; Саха, Гоутам (сентябрь 2020 г.). «Оптимизация набора фильтров на основе данных для автоматической проверки говорящего». Цифровая обработка сигналов. 104: 102795. arXiv:2007.10729. Дои:10.1016 / j.dsp.2020.102795. S2CID 220665533.
- ^ а б Ян, Иминь; Педерсен, Ян О. (1997). Сравнительное исследование выбора функций при категоризации текста (PDF). ICML.
- ^ Урбанович, Райан Дж .; Микер, Мелисса; ЛаКава, Уильям; Olson, Randal S .; Мур, Джейсон Х. (2018). «Выбор рельефа: введение и обзор». Журнал биомедицинской информатики. 85: 189–203. arXiv:1711.08421. Дои:10.1016 / j.jbi.2018.07.014. ЧВК 6299836. PMID 30031057.
- ^ Форман, Джордж (2003). «Обширное эмпирическое исследование показателей выбора функций для классификации текста» (PDF). Журнал исследований в области машинного обучения. 3: 1289–1305.
- ^ Иши Чжан; Шуцзюань Ли; Тэн Ван; Зиган Чжан (2013). «Отбор признаков по дивергенции для отдельных классов». Нейрокомпьютинг. 101 (4): 32–42. Дои:10.1016 / j.neucom.2012.06.036.
- ^ Guyon I .; Вестон Дж .; Barnhill S .; Вапник В. (2002). «Выбор гена для классификации рака с использованием машин опорных векторов». Машинное обучение. 46 (1–3): 389–422. Дои:10.1023 / А: 1012487302797.
- ^ Бах, Фрэнсис R (2008). Болассо: модель согласованной оценки лассо через бутстрап. Материалы 25-й Международной конференции по машинному обучению. С. 33–40. Дои:10.1145/1390156.1390161. ISBN 9781605582054. S2CID 609778.
- ^ Заре, Хабил (2013). «Оценка релевантности функций на основе комбинаторного анализа Лассо с применением для диагностики лимфомы». BMC Genomics. 14: S14. Дои:10.1186 / 1471-2164-14-S1-S14. ЧВК 3549810. PMID 23369194.
- ^ Кай Хан; Юньхэ Ван; Чао Чжан; Чао Ли; Чао Сюй (2018). Автоэнкодер вдохновлен неконтролируемым выбором функций. Международная конференция IEEE по акустике, обработке речи и сигналов (ICASSP).
- ^ Хазиме, Хусейн; Мазумдер, Рахул; Сааб, Али (2020). «Разреженная регрессия в масштабе: ветвление и граница, основанная на оптимизации первого порядка». arXiv:2004.06152 [stat.CO ].
- ^ Суфан, Осман; Клефтогианнис, Димитриос; Калнис, Панос; Баич, Владимир Б. (26.02.2015). «DWFS: инструмент выбора функций оболочки на основе параллельного генетического алгоритма». PLOS ONE. 10 (2): e0117988. Bibcode:2015PLoSO..1017988S. Дои:10.1371 / journal.pone.0117988. ISSN 1932-6203. ЧВК 4342225. PMID 25719748.
- ^ Фигероа, Алехандро (2015). «Изучение эффективных функций для распознавания намерений пользователя, стоящих за веб-запросами». Компьютеры в промышленности. 68: 162–169. Дои:10.1016 / j.compind.2015.01.005.
- ^ Фигероа, Алехандро; Гюнтер Нойман (2013). Учимся ранжировать эффективные пересказы из журналов запросов для ответов на вопросы сообщества. AAAI.
- ^ Фигероа, Алехандро; Гюнтер Нойман (2014). «Категориальные модели для ранжирования эффективных пересказов в ответах на вопросы сообщества». Экспертные системы с приложениями. 41 (10): 4730–4742. Дои:10.1016 / j.eswa.2014.02.004. HDL:10533/196878.
- ^ а б Zhang, Y .; Wang, S .; Филлипс, П. (2014). «Двоичный PSO с оператором мутации для выбора функции с использованием дерева решений, применяемого для обнаружения спама». Системы, основанные на знаниях. 64: 22–31. Дои:10.1016 / j.knosys.2014.03.015.
- ^ F.C. Гарсия-Лопес, М. Гарсия-Торрес, Б. Мелиан, Дж. А. Морено-Перес, Дж.М. Морено-Вега. Решение проблемы выбора подмножества признаков с помощью параллельного точечного поиска, Европейский журнал операционных исследований, т. 169, нет. 2. С. 477–489, 2006.
- ^ F.C. Гарсия-Лопес, М. Гарсия-Торрес, Б. Мелиан, Дж. А. Морено-Перес, Дж.М. Морено-Вега. Решение проблемы выбора подмножества признаков с помощью гибридной метаэвристики. В Первый международный семинар по гибридной метаэвристике, 2004, с. 59–68.
- ^ М. Гарсия-Торрес, Ф. Гомес-Вела, Б. Мелиан, Дж. М. Морено-Вега. Выбор пространственных объектов с помощью группировки объектов: подход к поиску переменных окрестностей, Информационные науки, т. 326, стр. 102-118, 2016.
- ^ Красков, Александр; Штегбауэр, Харальд; Анджеяк, Ральф Джи; Грассбергер, Питер (2003). «Иерархическая кластеризация на основе взаимной информации». arXiv:q-bio / 0311039. Bibcode:2003q.bio .... 11039K. Цитировать журнал требует
| журнал =(помощь) - ^ Акаике, Х. (1985), «Предсказание и энтропия», в Atkinson, A.C .; Файнберг, С.Э. (ред.), Праздник статистики (PDF), Springer, стр. 1–24..
- ^ Burnham, K. P .; Андерсон, Д. Р. (2002), Выбор модели и многомодельный вывод: практический теоретико-информационный подход (2-е изд.), Springer-Verlag, ISBN 9780387953649.
- ^ Эйнике, Г. А. (2018). «Выбор максимальной скорости энтропии признаков для классификации изменений в динамике коленного и голеностопного суставов во время бега». Журнал IEEE по биомедицинской и медицинской информатике. 28 (4): 1097–1103. Дои:10.1109 / JBHI.2017.2711487. PMID 29969403. S2CID 49555941.
- ^ Алиферис, Константин (2010). «Локальная причинная и марковская бланкетная индукция для выявления причин и выбора признаков для классификации, часть I: алгоритмы и эмпирическая оценка» (PDF). Журнал исследований в области машинного обучения. 11: 171–234.
- ^ а б c d Браун, Гэвин; Покок, Адам; Чжао, Мин-Цзе; Лухан, Микель (2012). «Максимизация условного правдоподобия: объединяющая основа для выбора теоретических характеристик информации». Журнал исследований в области машинного обучения. 13: 27–66.[1]
- ^ Peng, H.C .; Long, F .; Дин, К. (2005). «Выбор функций на основе взаимной информации: критерии максимальной зависимости, максимальной релевантности и минимальной избыточности». IEEE Transactions по анализу шаблонов и машинному анализу. 27 (8): 1226–1238. CiteSeerX 10.1.1.63.5765. Дои:10.1109 / TPAMI.2005.159. PMID 16119262. S2CID 206764015. Программа
- ^ Нгуен, Х., Франке, К., Петрович, С. (2010). «На пути к универсальной мере выбора функций для обнаружения вторжений», In Proc. Международная конференция по распознаванию образов (ICPR), Стамбул, Турция. [2]
- ^ Родригес-Лухан, I .; Huerta, R .; Elkan, C .; Санта-Крус, К. (2010). «Выбор функции квадратичного программирования» (PDF). JMLR. 11: 1491–1516.
- ^ а б Нгуен X. Винь, Джеффри Чан, Симоне Романо и Джеймс Бейли, «Эффективные глобальные подходы к выбору функций на основе взаимной информации». Материалы 20-й конференции ACM SIGKDD по открытию знаний и интеллектуальному анализу данных (KDD'14), 24–27 августа, Нью-Йорк, 2014 г. »[3] "
- ^ Ян, Говард Хуа; Муди, Джон (2000). «Визуализация данных и выбор функций: новые алгоритмы для негауссовских данных» (PDF). Достижения в системах обработки нейронной информации: 687–693.
- ^ Yamada, M .; Jitkrittum, W .; Sigal, L .; Xing, E.P .; Сугияма, М. (2014). «Выбор объектов большой размерности с помощью точного нелинейного лассо». Нейронные вычисления. 26 (1): 185–207. arXiv:1202.0515. Дои:10.1162 / NECO_a_00537. PMID 24102126. S2CID 2742785.
- ^ Холл, М. (1999). Выбор функций на основе корреляции для машинного обучения (PDF) (Кандидатская диссертация). Университет Вайкато.
- ^ Сенлиол, Барис; и другие. (2008). «Фильтр на основе быстрой корреляции (FCBF) с другой стратегией поиска». 2008 23-й Международный симпозиум по компьютерным и информационным наукам: 1–4. Дои:10.1109 / ISCIS.2008.4717949. ISBN 978-1-4244-2880-9. S2CID 8398495.
- ^ Нгуен, Хай; Франке, Катрин; Петрович, Слободан (декабрь 2009 г.). «Оптимизация класса мер выбора характеристик». Труды семинара NIPS 2009 по дискретной оптимизации в машинном обучении: субмодульность, разреженность и многогранники (DISCML). Ванкувер, Канада.
- ^ а б Х. Дэн, Дж. Рангер "Выбор функций через регулярные деревья ", Труды Международной совместной конференции по нейронным сетям (IJCNN) 2012 г., IEEE, 2012 г.
- ^ а б RRF: Регуляризованный случайный лес, р пакет на КРАН
- ^ а б Хамон, Джули (ноябрь 2013 г.). Комбинация оптимизации для выбора переменных в большом измерении: Application en génétique animale (Диссертация) (на французском языке). Лилльский университет науки и технологий.
- ^ Ю, Лэй; Лю, Хуань (август 2003 г.). «Выбор функций для данных большой размерности: решение для быстрой фильтрации на основе корреляции» (PDF). ICML'03: Материалы двадцатой международной конференции по машинному обучению: 856–863.
- ^ а б Т. М. Фыонг, З. Лин и Р. Б. Альтман. Выбор SNP с помощью выбора функций. В архиве 2016-09-13 в Wayback Machine Труды / Конференция по биоинформатике вычислительных систем IEEE, CSB. Конференция по биоинформатике вычислительных систем IEEE, страницы 301-309, 2005. PMID 16447987.
- ^ Saghapour, E .; Kermani, S .; Сеххати, М. (2017). «Новый метод ранжирования признаков для прогнозирования стадий рака с использованием данных протеомики». PLOS ONE. 12 (9): e0184203. Bibcode:2017PLoSO..1284203S. Дои:10.1371 / journal.pone.0184203. ЧВК 5608217. PMID 28934234.
- ^ Shah, S.C .; Кусяк, А. (2004). «Интеллектуальный анализ данных и генетический алгоритм на основе выбора гена / SNP». Искусственный интеллект в медицине. 31 (3): 183–196. Дои:10.1016 / j.artmed.2004.04.002. PMID 15302085.
- ^ Long, N .; Gianola, D .; Вейгель, К. А (2011). «Снижение размеров и выбор переменных для геномного отбора: приложение для прогнозирования надоев у голштинов». Журнал животноводства и генетики. 128 (4): 247–257. Дои:10.1111 / j.1439-0388.2011.00917.x. PMID 21749471.
- ^ Устюнкар, Гюркан; Özöür-Akyüz, Süreyya; Вебер, Герхард В .; Фридрих, Кристоф М .; Айдын Сон, Йешим (2012). «Выбор репрезентативных наборов SNP для полногеномных ассоциативных исследований: метаэвристический подход». Письма об оптимизации. 6 (6): 1207–1218. Дои:10.1007 / s11590-011-0419-7. S2CID 8075318.
- ^ Meiri, R .; Захави, Дж. (2006). «Использование имитации отжига для оптимизации проблемы выбора функций в маркетинговых приложениях». Европейский журнал операционных исследований. 171 (3): 842–858. Дои:10.1016 / j.ejor.2004.09.010.
- ^ Капетаниос, Г. (2007). «Выбор переменных в регрессионных моделях с использованием нестандартной оптимизации информационных критериев». Вычислительная статистика и анализ данных. 52 (1): 4–15. Дои:10.1016 / j.csda.2007.04.006.
- ^ Broadhurst, D .; Goodacre, R .; Jones, A .; Rowland, J. J .; Келл, Д. Б. (1997). «Генетические алгоритмы как метод выбора переменных в множественной линейной регрессии и частичной регрессии наименьших квадратов, с приложениями к масс-спектрометрии пиролиза». Analytica Chimica Acta. 348 (1–3): 71–86. Дои:10.1016 / S0003-2670 (97) 00065-2.
- ^ Chuang, L.-Y .; Ян, Ч.-Х. (2009). «Поиск табу и оптимизация роя бинарных частиц для выбора характеристик с использованием данных микрочипа». Журнал вычислительной биологии. 16 (12): 1689–1703. Дои:10.1089 / cmb.2007.0211. PMID 20047491.
- ^ Э. Альба, Дж. Гариа-Нието, Л. Журдан и Э.-Г. Талби. Выбор гена в классификации рака с использованием гибридных алгоритмов PSO-SVM и GA-SVM. Конгресс по эволюционным вычислениям, Singapor: Singapore (2007), 2007
- ^ Б. Дюваль, Ж.-К. Hao et J. C. Hernandez Hernandez. Меметический алгоритм выбора гена и молекулярной классификации рака. В материалах 11-й ежегодной конференции по генетическим и эволюционным вычислениям, GECCO '09, страницы 201-208, Нью-Йорк, Нью-Йорк, США, 2009. ACM.
- ^ К. Ханс, А. Добра и М. Вест. Стохастический поиск дробовика для регрессии 'большой p'. Журнал Американской статистической ассоциации, 2007 г.
- ^ Айткен, С. (2005). «Выбор характеристик и классификация для анализа данных микрочипов: эволюционные методы идентификации генов предсказания». BMC Bioinformatics. 6 (1): 148. Дои:10.1186/1471-2105-6-148. ЧВК 1181625. PMID 15958165.
- ^ Ой, И. С .; Мун, Б. Р. (2004). «Гибридные генетические алгоритмы для отбора признаков». IEEE Transactions по анализу шаблонов и машинному анализу. 26 (11): 1424–1437. CiteSeerX 10.1.1.467.4179. Дои:10.1109 / тпами.2004.105. PMID 15521491.
- ^ Xuan, P .; Guo, M. Z .; Wang, J .; Лю, X. Y .; Лю, Ю. (2011). «Выбор эффективных признаков на основе генетического алгоритма для классификации пре-миРНК». Генетика и молекулярные исследования. 10 (2): 588–603. Дои:10.4238 / vol10-2gmr969. PMID 21491369.
- ^ Пэн, С. (2003). «Молекулярная классификация типов рака по данным микрочипов с использованием комбинации генетических алгоритмов и опорных векторных машин». Письма FEBS. 555 (2): 358–362. Дои:10.1016 / s0014-5793 (03) 01275-4. PMID 14644442.
- ^ Hernandez, J.C.H .; Duval, B .; Хао, Ж.-К. (2007). «Встроенный генетический подход для отбора генов и классификации данных микрочипов». Эволюционные вычисления, машинное обучение и интеллектуальный анализ данных в биоинформатике. EvoBIO 2007. Конспект лекций по информатике. том 4447. Берлин: Springer Verlag. С. 90–101. Дои:10.1007/978-3-540-71783-6_9. ISBN 978-3-540-71782-9.
- ^ Huerta, E.B .; Duval, B .; Хао, Ж.-К. (2006). «Гибридный подход GA / SVM для отбора генов и классификации данных микрочипов». Приложения эволюционных вычислений. EvoWorkshops 2006. Конспект лекций по информатике. vol 3907. pp. 34–44. Дои:10.1007/11732242_4. ISBN 978-3-540-33237-4.
- ^ Muni, D. P .; Pal, N.R .; Дас, Дж. (2006). «Генетическое программирование для одновременного выбора признаков и построения классификатора». IEEE Transactions по системам, человеку и кибернетике - Часть B: Кибернетика: Кибернетика. 36 (1): 106–117. Дои:10.1109 / TSMCB.2005.854499. PMID 16468570. S2CID 2073035.
- ^ Jourdan, L .; Dhaenens, C .; Талби, Э.-Г. (2005). «Исследование неравновесия сцепления с параллельным адаптивным GA». Международный журнал основ информатики. 16 (2): 241–260. Дои:10.1142 / S0129054105002978.
- ^ Zhang, Y .; Dong, Z .; Phillips, P .; Ван, С. (2015). «Обнаружение субъектов и областей мозга, связанных с болезнью Альцгеймера, с помощью 3D-МРТ на основе собственного мозга и машинного обучения». Границы вычислительной нейробиологии. 9: 66. Дои:10.3389 / fncom.2015.00066. ЧВК 4451357. PMID 26082713.
- ^ Roffo, G .; Melzi, S .; Кристани, М. (01.12.2015). Бесконечный выбор функций. Международная конференция IEEE по компьютерному зрению (ICCV), 2015 г.. С. 4202–4210. Дои:10.1109 / ICCV.2015.478. ISBN 978-1-4673-8391-2. S2CID 3223980.
- ^ Роффо, Джорджио; Мельци, Симона (сентябрь 2016 г.). «Выбор функций через центральность собственного вектора» (PDF). NFmcp2016. Получено 12 ноября 2016.
- ^ Р. Кохави и Дж. Джон "Оболочки для выбора подмножества функций ", Искусственный интеллект 97.1-2 (1997): 273-324
- ^ Дас, Абхиманью; Кемпе, Дэвид (2011). «Подмодуль встречается со спектральным: жадные алгоритмы для выбора подмножества, разреженной аппроксимации и выбора словаря». arXiv:1102.3975 [stat.ML ].
- ^ Лю и др., Выбор субмодульных функций для акустических партитур большого размера В архиве 2015-10-17 на Wayback Machine
- ^ Чжэн и др., Выбор субмодульных атрибутов для распознавания действий в видео В архиве 2015-11-18 на Wayback Machine
- ^ Sun, Y .; Todorovic, S .; Гудисон, С. (2010). «[https://ieeexplore.ieee.org/abstract/document/5342431/ Выбор функций на основе местного обучения для анализа данных большого размера]». IEEE Transactions по анализу шаблонов и машинному анализу. 32 (9): 1610–1626. Дои:10.1109 / тпами.2009.190. ЧВК 3445441. PMID 20634556. Внешняя ссылка в
| название =(помощь) - ^ D.H. Wang, Y.C. Лян, Д. Сюй, X.Y. Фэн, Р. Гуань (2018) "Контентная рекомендательная система для публикаций по информатике ", Системы, основанные на знаниях, 157: 1-9
дальнейшее чтение
- Гийон, Изабель; Элиссефф, Андре (2003). «Введение в выбор переменных и функций». Журнал исследований в области машинного обучения. 3: 1157–1182.
- Харрелл, Ф. (2001). Стратегии регрессионного моделирования. Springer. ISBN 0-387-95232-2.
- Лю, Хуань; Мотода, Хироши (1998). Выбор функций для обнаружения знаний и интеллектуального анализа данных. Springer. ISBN 0-7923-8198-X.
- Лю, Хуань; Ю, Лей (2005). «На пути к интеграции алгоритмов выбора признаков для классификации и кластеризации». IEEE Transactions по разработке знаний и данных. 17 (4): 491–502. Дои:10.1109 / TKDE.2005.66. S2CID 1607600.
внешняя ссылка
- Пакет выбора функций, Университет штата Аризона (код Matlab)
- NIPS Challenge 2003 (смотрите также НИПС )
- Наивная реализация Байеса с выбором функций в Visual Basic (включает исполняемый файл и исходный код)
- Программа выбора функций с минимальной избыточностью и максимальной релевантностью (mRMR)
- ПРАЗДНИК (Алгоритмы выбора функций с открытым исходным кодом в C и MATLAB)












![mathrm {mRMR} = max _ {S} left [{ frac {1} {| S |}} sum _ {f_ {i} in S} I (f_ {i}; c) - { frac {1} {| S | ^ {2}}} sum _ {f_ {i}, f_ {j} in S} I (f_ {i}; f_ {j}) right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/3eec7b98cd9e6fc9b3b61c0ac4712a16379c8859)


![mathrm {mRMR} = max _ {x in {0,1 } ^ {n}} left [{ frac { sum _ {i = 1} ^ {n} c_ {i} x_ { i}} { sum _ {i = 1} ^ {n} x_ {i}}} - { frac { sum _ {i, j = 1} ^ {n} a_ {ij} x_ {i} x_ {j}} {( sum _ {i = 1} ^ {n} x_ {i}) ^ {2}}} right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/0baef01e8c550ba917099a82e0ac43e826f59d37)

![F_ {n times 1} = [I (f_ {1}; c), ldots, I (f_ {n}; c)] ^ {T}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e655a9d669fdf3ca7c6572563f8b5d1c1d7af44e)
![H_ {n times n} = [I (f_ {i}; f_ {j})] _ {i, j = 1 ldots n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5d1966a8fa8bd4894b5d768dcfc4da9b1caa9de)





![{ displaystyle { begin {align} JMI (f_ {i}) & = sum _ {f_ {j} in S} (I (f_ {i}; c) + I (f_ {i}; c | f_ {j})) & = sum _ {f_ {j} in S} { bigl [} I (f_ {j}; c) + I (f_ {i}; c) - { bigl (} I (f_ {i}; f_ {j}) - I (f_ {i}; f_ {j} | c) { bigr)} { bigr]} end {выравнивается}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c44f7ace0374e11b551d8a9f254513a1cb431d1)






















![{ displaystyle mathrm {CFS} = max _ {S_ {k}} left [{ frac {r_ {cf_ {1}} + r_ {cf_ {2}} + cdots + r_ {cf_ {k}} }} { sqrt {k + 2 (r_ {f_ {1} f_ {2}} + cdots + r_ {f_ {i} f_ {j}} + cdots + r_ {f_ {k} f_ {k- 1}})}}} right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83568ac8d01463888fbfb13c56c9dd32a790699e)


![mathrm {CFS} = max _ {x in {0,1 } ^ {n}} left [{ frac {( sum _ {i = 1} ^ {n} a_ {i} x_ {i}) ^ {2}} { sum _ {i = 1} ^ {n} x_ {i} + sum _ {i neq j} 2b_ {ij} x_ {i} x_ {j}}} верно].](https://wikimedia.org/api/rest_v1/media/math/render/svg/9491bc46548bd4416952e59704e78388e8726480)
