Решетка Браве - Bravais lattice

В геометрия и кристаллография, а Решетка Браве, названный в честь Огюст Браве (1850 ),^[1] бесконечный массив дискретных точек, порожденный набором дискретный перевод операции, описанные в трехмерном пространстве:

{ displaystyle mathbf {R} = n_ {1} mathbf {a} _ {1} + n_ {2} mathbf {a} _ {2} + n_ {3} mathbf {a} _ {3} }

(1)

где п_я любые целые числа и а_я находятся примитивные векторы которые лежат в разных направлениях (не обязательно взаимно перпендикулярно) и охватывают решетку. Выбор примитивных векторов для данной решетки Браве не уникален. Фундаментальный аспект любой решетки Браве состоит в том, что при любом выборе направления решетка будет выглядеть точно такой же из каждой дискретной точки решетки, если смотреть в этом выбранном направлении.

В кристаллографии концепция решетки Браве о бесконечном массиве дискретных точек расширяется с использованием концепции ячейка который включает пространство между точками дискретной решетки, а также любые атомы в этом пространстве. Есть два основных типа элементарных ячеек: примитивные элементарные ячейки и непримитивные элементарные ячейки.

Примитивная элементарная ячейка для данной решетки Браве может быть выбрана более чем одним способом (каждый способ имеет разную форму), но каждый способ будет иметь одинаковый объем и каждый способ будет обладать тем свойством, что взаимно однозначное соответствие может между примитивными элементарными ячейками и точками дискретной решетки. Очевидная примитивная клетка, которую нужно связать с определенным выбором примитивных векторов, - это сформированный ими параллелепипед.^[2] То есть набор всех точек р формы:

{ displaystyle mathbf {r} = x_ {1} mathbf {a} _ {1} + x_ {2} mathbf {a} _ {2} + x_ {3} mathbf {a} _ {3} qquad { text {где}} 0 leq x_ {i} <1}

(2)

Недостатком использования параллелепипеда, определяемого примитивными векторами, в качестве элементарной ячейки в некоторых случаях является нечеткое выявление полной симметрии решетки. Одно из решений - использовать Примитивная ячейка Вигнера-Зейтца (состоящий из всех точек в пространстве, которые ближе к данной точке решетки, чем к любой другой точке решетки), который действительно показывает полную симметрию решетки. Другое решение - использовать непримитивная элементарная ячейка что действительно показывает полную симметрию решетки. Непримитивный объем элементарной ячейки будет целым числом, кратным объему элементарной элементарной ячейки.

Элементарная ячейка, примитивная или нет, при однократном воспроизведении для каждой дискретной точки решетки должна точно заполнять все пространство без перекрытия и зазоров.

Расширенная концепция решетки Браве, включая элементарную ячейку, используется для формального определения кристаллическое расположение и его (конечные) границы. А кристалл состоит из периодического расположения одного или нескольких атомов ( основа или мотив), встречающийся ровно один раз в каждой примитивной элементарной ячейке. В основа может состоять из атомы, молекулы, или полимер строки твердое вещество Следовательно, кристалл выглядит одинаково, если смотреть в любом заданном направлении из любых эквивалентных точек в двух разных элементарных ячейках (две точки в двух разных элементарных ячейках одной и той же решетки эквивалентны, если они имеют одинаковое относительное положение по отношению к их индивидуальной единице границы ячеек).

Две решетки Браве часто считаются эквивалентными, если они имеют изоморфные группы симметрии. В этом смысле существует 14 возможных решеток Браве в трехмерном пространстве. 14 возможных групп симметрии решеток Браве - это 14 из 230 космические группы. В контексте классификации пространственных групп решетки Браве также называются классами Браве, арифметическими классами Браве или стаями Браве.^[3]

В 2-х измерениях

Заметка: На следующих диаграммах точки решетки изображены зелеными кружками, а элементарные ячейки изображены параллелограммами (которые могут быть квадратами или прямоугольниками), обведенными черным контуром. Хотя каждый из четырех углов каждого параллелограмма соединяется с точкой решетки, технически только одна из четырех точек решетки принадлежит данной элементарной ячейке, а каждая из трех других точек решетки принадлежит одной из соседних элементарных ячеек. Это можно увидеть, представив, что параллелограмм элементарной ячейки перемещается немного влево и немного вниз, при этом все зеленые кружки точек решетки остаются неподвижными.

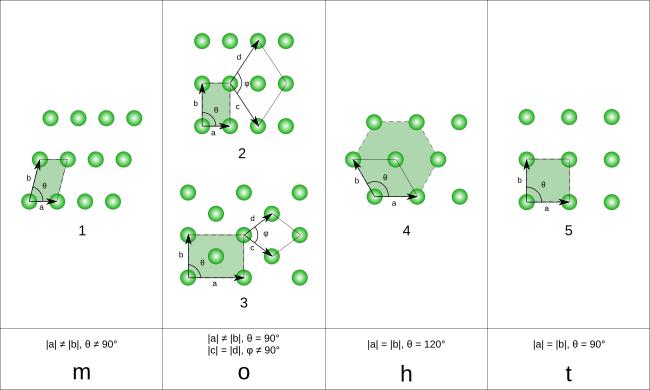
1 - косой (моноклинный), 2 - прямоугольный (ромбический), 3 - центрированный прямоугольный (ромбический), 4 - гексагональный и 5 - квадратный (четырехугольный).

В двумерном пространстве есть 5 решеток Браве,^[4] сгруппированы в четыре хрустальные семьи.

Кристальная семья	Группа точек (Обозначение Шенфлиса )	5 решеток Браве
Кристальная семья	Группа точек (Обозначение Шенфлиса )	Примитивный	По центру
Моноклиника	C₂	Косой
Орторомбический	D₂	Прямоугольный	Прямоугольник по центру
Шестиугольный	D₆	Шестиугольный
Тетрагональный	D₄	Квадрат

Элементарные ячейки задаются в соответствии с относительными длинами краев ячеек (а и б) и угол между ними (θ). Площадь элементарной ячейки можно рассчитать, оценив норма ||а × б||, где а и б - векторы решетки. Ниже приведены свойства семейств кристаллов:

Кристальная семья	Площадь	Осевые расстояния (длины кромок)	Осевой угол
Моноклиника	${ displaystyle ab , sin theta}$	а ≠ б	θ ≠ 90°
Орторомбический	${ displaystyle ab}$	а ≠ б	θ = 90°
Шестиугольный	${ displaystyle { frac { sqrt {3}} {2}} , a ^ {2}}$	а = б	θ = 120°
Тетрагональный	${ displaystyle a ^ {2}}$	а = б	θ = 90°

В 3-х измерениях

2 × 2 × 2 элементарные ячейки алмаз кубический решетка

В трехмерном пространстве есть 14 решеток Браве. Их можно получить, комбинируя один из семи решетчатые системы с одним из типов центровки. Типы центрирования определяют положение точек решетки в элементарной ячейке следующим образом:

Примитивный (P): точки решетки только на углах ячейки (иногда называемые простыми)
По центру основания (A, B или C): точки решетки на углах ячейки с одной дополнительной точкой в центре каждой грани одной пары параллельных граней ячейки (иногда называемые центрированными по концам)
По центру тела (I): точки решетки по углам ячейки, с одной дополнительной точкой в центре ячейки.
По центру грани (F): точки решетки на углах ячейки, с одной дополнительной точкой в центре каждой из граней ячейки.

Не все комбинации систем решеток и типов центрирования необходимы для описания всех возможных решеток, так как можно показать, что некоторые из них фактически эквивалентны друг другу. Например, моноклинная I-решетка может быть описана моноклинной C-решеткой путем различного выбора осей кристалла. Точно так же все A- или B-центрированные решетки можно описать либо C-, либо P-центрированием. Это сокращает количество комбинаций до 14 обычных решеток Браве, показанных в таблице ниже.^[5] Под каждой диаграммой Символ Пирсона для этой решетки Браве.

Заметка: На схемах элементарной ячейки в следующей таблице показаны все точки решетки на границе ячейки (углы и грани); однако технически не все эти точки решетки принадлежат данной элементарной ячейке. Это можно увидеть, представив, что элементарная ячейка слегка перемещается в отрицательном направлении каждой оси, сохраняя фиксированные точки решетки. Грубо говоря, это можно представить как перемещение элементарной ячейки немного влево, немного вниз и немного за пределы экрана. Это показывает, что только одна из восьми угловых точек решетки (а именно передняя, левая, нижняя) принадлежит данной элементарной ячейке (остальные семь точек решетки принадлежат соседним элементарным ячейкам). Кроме того, только одна из двух точек решетки, показанных на верхней и нижней грани в По центру основания столбец принадлежит данной элементарной ячейке. Наконец, только три из шести точек решетки на гранях в По центру лица столбец принадлежит данной элементарной ячейке.

Кристальная семья	Решетчатая система	Schönflies	14 решеток Браве
Кристальная семья	Решетчатая система	Schönflies	Примитивный (P)	По центру основания (C)	По центру тела (I)	По центру лица (F)
Триклиник		C_я	AP
Моноклиника		C_2ч	mP	РС
Орторомбический		D_2ч	oP	Операционные системы	oI	oF
Тетрагональный		D_4ч	tP		tI
Шестиугольный	Ромбоэдрический	D_3D	час
Шестиугольный	Шестиугольный	D_6ч	л.с.
Кубический		О_час	cP		cI	cF

Элементарные ячейки указаны в соответствии с шестью параметры решетки которые представляют собой относительные длины краев ячейки (а, б, c) и углы между ними (α, β, γ). Объем элементарной ячейки можно рассчитать, оценив тройное произведение а · (б × c), где а, б, и c - векторы решетки. Свойства решетчатых систем приведены ниже:

Кристальная семья	Решетчатая система	Объем	Осевые расстояния (длины кромок)^[6]	Осевые углы^[6]	Соответствующие примеры
Триклиник		${ displaystyle abc { sqrt {1- cos ^ {2} alpha - cos ^ {2} beta - cos ^ {2} gamma +2 cos alpha cos beta cos gamma }}}$	(Все остальные случаи)		K₂Cr₂О₇, CuSO₄· 5H₂О, ЧАС₃BO₃
Моноклиника		${ displaystyle abc , sin beta}$	а ≠ c	α = γ = 90°, β ≠ 90°	Моноклинная сера, Na₂ТАК₄· 10H₂О, PbCrO₃
Орторомбический		${ displaystyle abc}$	а ≠ б ≠ c	α = β = γ = 90°	Ромбическая сера, KNO₃, BaSO₄
Тетрагональный		${ displaystyle a ^ {2} c}$	а = б ≠ c	α = β = γ = 90°	Белая жесть, SnO₂, TiO₂, CaSO₄
Шестиугольный	Ромбоэдрический	${ displaystyle a ^ {3} { sqrt {1-3 cos ^ {2} alpha +2 cos ^ {3} alpha}}}$	а = б = c	α = β = γ ≠ 90°	Кальцит (CaCO₃), киноварь (HgS)
Шестиугольный	Шестиугольный	${ displaystyle { frac { sqrt {3}} {2}} , a ^ {2} c}$	а = б	α = β = 90°, γ = 120°	Графитовый, ZnO, CdS
Кубический		${ displaystyle a ^ {3}}$	а = б = c	α = β = γ = 90°	NaCl, цинковая обманка, медный металл, KCl, Алмаз, Серебряный

В 4-х измерениях

В четырех измерениях есть 64 решетки Браве. Из них 23 примитивные и 41 центрированные. Десять решеток Браве разбиваются на энантиоморфный пары.^[7]

Смотрите также

использованная литература

^ Aroyo, Mois I .; Мюллер, Ульрих; Вондрачек, Ганс (2006). «Историческое введение». Международные таблицы для кристаллографии. A1 (1.1): 2–5. CiteSeerX 10.1.1.471.4170. Дои:10.1107/97809553602060000537. Архивировано из оригинал на 2013-07-04. Получено 2008-04-21.
^ Эшкрофт, Нил В. (1976). "Глава 4". Физика твердого тела. Компания W. B. Saunders. п. 72. ISBN 0-03-083993-9.
^ "Браве класс". Интернет-словарь кристаллографии. IUCr. Получено 8 августа 2019.
^ Киттель, Чарльз (1996) [1953]. "Глава 1". Введение в физику твердого тела (Седьмое изд.). Нью-Йорк: Джон Вили и сыновья. п. 10. ISBN 978-0-471-11181-8. Получено 2008-04-21.
^ На основе списка обычных ячеек, найденных в Хан (2002), п. 744
^ ^а ^б Хан (2002), п. 758
^ Браун, Гарольд; Бюлов, Рольф; Нойбюзер, Иоахим; Вондрачек, Ганс; Цассенхаус, Ганс (1978), Кристаллографические группы четырехмерного пространства, Нью-Йорк: Wiley-Interscience [John Wiley & Sons], ISBN 978-0-471-03095-9, Г-Н 0484179

дальнейшее чтение

Браве, А. (1850). «Воспоминания о системах, сформированных по принципу распределения точек, регулирующего порядок на плане или в пространстве» [Воспоминания о системах, образованных точками, регулярно распределенными на плоскости или в пространстве]. J. École Polytech. 19: 1–128.CS1 maint: ref = harv (ссылка на сайт) (Английский язык: Memoir 1, Crystallographic Society of America, 1949.)
Хан, Тео, изд. (2002). Международные таблицы для кристаллографии, том A: Симметрия пространственных групп. Международные таблицы для кристаллографии. А (5-е изд.). Берлин, Нью-Йорк: Springer-Verlag. Дои:10.1107/97809553602060000100. ISBN 978-0-7923-6590-7.CS1 maint: ref = harv (ссылка на сайт)

внешние ссылки

Каталог решеток (Небе и Слоан)
Смит, Уолтер Фокс (2002). "Песня о решетках Браве".CS1 maint: ref = harv (ссылка на сайт)

[1] Aroyo, Mois I .; Мюллер, Ульрих; Вондрачек, Ганс (2006). «Историческое введение». Международные таблицы для кристаллографии. A1 (1.1): 2–5. CiteSeerX 10.1.1.471.4170. Дои:10.1107/97809553602060000537. Архивировано из оригинал на 2013-07-04. Получено 2008-04-21.

[2] Эшкрофт, Нил В. (1976). "Глава 4". Физика твердого тела. Компания W. B. Saunders. п. 72. ISBN 0-03-083993-9.

[3] "Браве класс". Интернет-словарь кристаллографии. IUCr. Получено 8 августа 2019.

[4] Киттель, Чарльз (1996) [1953]. "Глава 1". Введение в физику твердого тела (Седьмое изд.). Нью-Йорк: Джон Вили и сыновья. п. 10. ISBN 978-0-471-11181-8. Получено 2008-04-21.

[5] На основе списка обычных ячеек, найденных в Хан (2002), п. 744

[axial_dimensions-6] а ^б Хан (2002), п. 758

[7] Браун, Гарольд; Бюлов, Рольф; Нойбюзер, Иоахим; Вондрачек, Ганс; Цассенхаус, Ганс (1978), Кристаллографические группы четырехмерного пространства, Нью-Йорк: Wiley-Interscience [John Wiley & Sons], ISBN 978-0-471-03095-9, Г-Н 0484179

[1]

[2]

[3]

[4]

[5]

[6]

[7]