Биологическая модель нейрона - Biological neuron model

Рис. 1. Нейрон и миелинизированный аксон с потоком сигнала от входов на дендритах к выходам на окончаниях аксонов. Сигнал представляет собой короткий электрический импульс, называемый потенциалом действия или «всплеском».

Рис. 2. Динамика потенциала действия нейронов («спайк»). Обратите внимание, что амплитуда и точная форма потенциала действия могут варьироваться в зависимости от точной экспериментальной техники, используемой для получения сигнала.

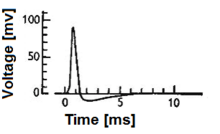
Биологические модели нейронов, также известный как пиковые модели нейронов,^[1] представляют собой математические описания свойств определенных клеток нервной системы, которые генерируют резкие электрические потенциалы. через их клеточную мембрану длительностью примерно одну миллисекунду, называемые потенциалами действия или пиками (рис. 2). Поскольку шипы передаются по аксон и синапсы от передающего нейрона ко многим другим нейронам, нейроны считаются основным блоком обработки информации нервная система. Модели нейронов с импульсами можно разделить на различные категории: наиболее подробными математическими моделями являются биофизические модели нейронов (также называемые моделями Ходжкина-Хаксли), которые описывают мембранное напряжение как функцию входного тока и активации ионных каналов. Математически более простыми являются модели «интегрировать и поджечь», которые описывают мембранное напряжение как функцию входного тока и предсказывают время всплесков без описания биофизических процессов, которые формируют временной ход потенциала действия. Даже более абстрактные модели предсказывают только всплески выходного сигнала (но не мембранного напряжения) в зависимости от стимуляции, при этом стимуляция может происходить через сенсорный ввод или фармакологически. В этой статье дается краткий обзор различных моделей нейронов с импульсами и ссылок, по возможности, на экспериментальные явления. Он включает детерминированные и вероятностные модели.

Введение: Биологические основы, классификация и цели нейронных моделей

Клетки без пиков, клетки с пиками и их измерение

Не все клетки нервной системы производят спайк, который определяет возможности моделей спайк-нейронов. Например, кохлеарный волосковые клетки, рецепторные клетки сетчатки, и биполярные клетки сетчатки не шипят. Кроме того, многие клетки нервной системы не классифицируются как нейроны, а вместо этого классифицируются как глия.

Активность нейронов можно измерить с помощью различных экспериментальных методов. Метод измерения «целая клетка», который фиксирует пиковую активность одного нейрона и производит потенциалы действия полной амплитуды.

При внеклеточных методах измерения электрод (или набор из нескольких электродов) располагается во внеклеточном пространстве. Пики, часто от нескольких источников выбросов, в зависимости от размера электрода и его близости к источникам, могут быть идентифицированы с помощью методов обработки сигналов. Внеклеточные измерения имеют несколько преимуществ: 1) их легче получить экспериментально; 2) Надежен и служит дольше; 3) Может отражать доминирующий эффект, особенно когда проводится в анатомической области с множеством похожих клеток.

Обзор моделей нейронов

Модели нейронов можно разделить на две категории в зависимости от физических единиц интерфейса модели. Каждую категорию можно дополнительно разделить по уровню абстракции / детализации:

1. Электрические модели ввода-вывода мембранного напряжения - Эти модели позволяют прогнозировать выходное напряжение мембраны в зависимости от электростимуляции, заданной как входной ток или напряжение. Различные модели в этой категории отличаются точным функциональным соотношением между входным током и выходным напряжением, а также уровнем детализации. Некоторые модели в этой категории предсказывают только момент возникновения всплеска выпуска (также известного как «потенциал действия»); другие модели более подробны и учитывают субклеточные процессы. Модели в этой категории могут быть детерминированными или вероятностными.
2. Естественный стимул или фармакологические модели входных нейронов - Модели в этой категории связывают входной стимул, который может быть фармакологическим или естественным, с вероятностью всплеска. Входной каскад этих моделей не является электрическим, а имеет либо фармакологические (химические) единицы концентрации, либо физические единицы, которые характеризуют внешний раздражитель, такой как свет, звук или другие формы физического давления. Кроме того, выходной каскад отражает вероятность выброса, а не электрического напряжения.

Хотя в науке и технике нет ничего необычного в наличии нескольких описательных моделей для разных уровней абстракции / детализации, количество различных, иногда противоречащих друг другу биологических моделей нейронов исключительно велико. Эта ситуация частично является результатом множества различных экспериментальных настроек и сложности отделения внутренних свойств отдельного нейрона от результатов измерений и взаимодействий многих клеток (сеть последствия). Чтобы ускорить переход к единой теории, мы перечисляем несколько моделей в каждой категории и, где это возможно, также ссылки на поддерживающие эксперименты.

Цели нейронных моделей

В конечном счете, биологические модели нейронов призваны объяснить механизмы, лежащие в основе работы нервной системы. Моделирование помогает анализировать экспериментальные данные и решать такие вопросы, как: Как спайки нейрона связаны с сенсорной стимуляцией или двигательной активностью, такой как движения рук? Какой нейронный код использует нервная система? Модели также важны в контексте восстановления утраченных функций мозга с помощью нейропротез устройств.

Модели электрического ввода-вывода мембранного напряжения

Модели этой категории описывают взаимосвязь между мембранными токами нейронов на входном каскаде и мембранным напряжением на выходном каскаде. В эту категорию входят (обобщенные) модели «интегрировать и запустить» и биофизические модели, вдохновленные работой Ходжкина-Хаксли в начале 1950-х годов с использованием экспериментальной установки, которая прокалывала клеточную мембрану и позволяла вызвать определенное напряжение / ток мембраны.^[2][3][4][5]

Самый современный электрические нейронные интерфейсы применяйте внеклеточную электрическую стимуляцию, чтобы избежать повреждения мембраны, которое может привести к гибели клеток и повреждению тканей. Следовательно, неясно, в какой степени электрические модели нейронов подходят для внеклеточной стимуляции (см., Например,^[6]).

Ходжкина – Хаксли

Экспериментальные доказательства, подтверждающие модель

Свойство модели H&H	Рекомендации
Форма индивидуального шипа	[2][3][4][5]
Идентичность участвующих ионов	[2][3][4][5]
Пиковая скорость по аксону	[2]

Основная статья: Модель Ходжкина – Хаксли

Модель Ходжкина – Хаксли (модель H&H)^[2][3][4][5]представляет собой модель взаимосвязи между потоком ионных токов через мембрану нейрональной клетки и мембранным напряжением клетки.^[2][3][4][5] Он состоит из набора нелинейный дифференциальные уравнения описывая поведение ионных каналов, проникающих через клеточную мембрану гигантский аксон кальмара. За эту работу Ходжкин и Хаксли были удостоены Нобелевской премии 1963 года по физиологии и медицине.

Мы отмечаем зависимость напряжения от тока с множественными зависимыми от напряжения токами, заряжающими клеточную мембрану емкости. C_м

${\displaystyle C_{\mathrm {m} }{\frac {dV(t)}{dt}}=-\sum _{i}I_{i}(t,V)}$.

Вышеприведенное уравнение - это время производная закона емкость, Q = резюме где изменение полного заряда следует объяснять как сумму по токам. Каждый ток определяется

${\displaystyle I(t,V)=g(t,V)\cdot (V-V_{\mathrm {eq} })}$

куда грамм(т,V) это проводимость, или обратное сопротивление, которое может быть увеличено до максимальной проводимости грамм и фракции активации и инактивации м и чассоответственно, которые определяют, сколько ионов может пройти через доступные мембранные каналы. Это расширение дается

${\displaystyle g(t,V)={\bar {g}}\cdot m(t,V)^{p}\cdot h(t,V)^{q}}$

и наши фракции следуют кинетике первого порядка

${\displaystyle {\frac {dm(t,V)}{dt}}={\frac {m_{\infty }(V)-m(t,V)}{\tau _{\mathrm {m} }(V)}}=\alpha _{\mathrm {m} }(V)\cdot (1-m)-\beta _{\mathrm {m} }(V)\cdot m}$

с аналогичной динамикой для час, где мы можем использовать либо τ и м_∞ или же α и β чтобы определить наши доли ворот.

Модель Ходжкина – Хаксли может быть расширена за счет включения дополнительных ионных токов. Обычно они включают поступающий внутрь Ca²⁺ и Na⁺ входные токи, а также несколько разновидностей К⁺ исходящие токи, в том числе ток «утечки».

Конечным результатом может быть около 20 параметров, которые необходимо оценить или измерить для получения точной модели. Для сложных систем нейронов интеграция уравнений требует больших вычислительных ресурсов. Поэтому необходимы тщательные упрощения модели Ходжкина – Хаксли.

Идеальная интеграция и огонь

Одна из самых ранних моделей нейрона - это совершенная модель интеграции и возбуждения (также называемая без утечки, интеграция и возбуждение), впервые исследованная в 1907 г. Луи Лапик.^[7] Нейрон представлен его мембранным напряжением. V которое вовлекает во время стимуляции входным током Это) согласно

${\displaystyle I(t)=C{\frac {dV(t)}{dt}}}$

что как раз то время производная закона емкость, Q = резюме. Когда подается входной ток, мембранное напряжение увеличивается со временем, пока не достигнет постоянного порога. V_th, в этот момент a дельта-функция происходит всплеск, и напряжение сбрасывается до своего потенциала покоя, после чего модель продолжает работать. В частота стрельбы модели, таким образом, неограниченно линейно увеличивается по мере увеличения входного тока.

Модель можно сделать более точной, если ввести период отражения т_ссылка это ограничивает частоту срабатывания нейрона, предотвращая его срабатывание в течение этого периода. Для постоянного ввода I (t) = I пороговое напряжение достигается по истечении времени интегрирования т_int= CV_чт/Я после старта с нуля. После сброса рефрактерный период вводит мертвое время, так что общее время до следующего обжига составляет т_ссылка+т_int . Частота срабатывания обратна полному интервалу между импульсами (включая мертвое время). Таким образом, частота зажигания как функция постоянного входного тока равна

${\displaystyle \,\!f(I)={\frac {I}{C_{\mathrm {} }V_{\mathrm {th} }+t_{\mathrm {ref} }I}}}$.

Недостатком этой модели является то, что она не описывает ни адаптации, ни утечки. Если в какое-то время модель получит короткий импульс тока ниже порогового значения, она сохранит это повышение напряжения навсегда - до тех пор, пока другой вход не заставит ее сработать. Эта характеристика явно не соответствует наблюдаемому поведению нейронов. Следующие расширения делают модель «интегрировать и запустить» более правдоподобной с биологической точки зрения.

Дырявый интегрируй и зажигай

Протекающая модель интеграции и возгорания, восходящая к Луи Лапик,^[7] по сравнению с моделью «интегрировать и воспламенить» без утечки содержит член «утечки» в уравнении мембранного потенциала, отражающий диффузию ионов через мембрану. Уравнение модели выглядит как^[1]

${\displaystyle C_{\mathrm {m} }{\frac {dV_{\mathrm {m} }(t)}{dt}}=I(t)-{\frac {V_{\mathrm {m} }(t)}{R_{\mathrm {m} }}}}$

Нейрон представлен RC-цепью с порогом. Каждый входной импульс (например, вызванный выбросом от другого нейрона) вызывает короткий импульс тока. Напряжение спадает экспоненциально. При достижении порогового значения генерируется всплеск на выходе, и напряжение сбрасывается.

куда V_м - напряжение на клеточной мембране и р_м сопротивление мембраны. (Модель интеграции и возгорания без утечек извлекается в пределе р_м до бесконечности, т.е.если мембрана является идеальным изолятором). Уравнение модели действительно для произвольного зависящего от времени входа до порога V_th достигается; после этого мембранный потенциал сбрасывается.

Для постоянного входа минимальный вход для достижения порога равен я_th = V_th / р_м. Предполагая сброс на ноль, частота срабатывания выглядит как

${\displaystyle f(I)={\begin{cases}0,&I\leq I_{\mathrm {th} }\\{[}t_{\mathrm {ref} }-R_{\mathrm {m} }C_{\mathrm {m} }\log(1-{\tfrac {V_{\mathrm {th} }}{IR_{\mathrm {m} }}}){]}^{-1},&I>I_{\mathrm {th} }\end{cases}}}$

который сходится при больших входных токах к предыдущей модели без утечек с рефрактерным периодом.^[8] Модель также может быть использована для тормозных нейронов. ^[9][10]

Самым большим недостатком нейрона «Дырявый» является то, что он не содержит нейронной адаптации, поэтому он не может описать экспериментально измеренную последовательность всплесков в ответ на постоянный входной ток.^[11] Этот недостаток устранен в обобщенных моделях интеграции и запуска, которые также содержат одну или несколько переменных адаптации и могут с высокой степенью точности прогнозировать время спайков кортикальных нейронов при введении тока.^[12][13][14]

Внешняя ссылка:

дырявая модель интеграции и возгорания, (Глава 4.1 в учебнике 'Spiking Neuron Models^[1])

Адаптивная интеграция и огонь

Экспериментальные доказательства, подтверждающие модель

Модель модели Adaptive Integrate-and-fire	Рекомендации
Допороговое напряжение для зависящего от времени входного тока	[13][14]
Время включения для зависящего от времени входного тока	[13][14]
Схемы срабатывания в ответ на ввод пошагового тока	[15][16][17]

Под адаптацией нейронов понимается тот факт, что даже при наличии постоянного тока, вводимого в некоторые, интервалы между выбросами на выходе увеличиваются. Адаптивная модель нейрона интеграции и запуска сочетает в себе утечку интеграции напряжения V с одной или несколькими переменными адаптации ш_k (см. главу 6.1 в учебнике Нейронная динамика).^[18])

${\displaystyle \tau _{\mathrm {m} }{\frac {dV_{\mathrm {m} }(t)}{dt}}=RI(t)-[V_{\mathrm {m} }(t)-E_{\mathrm {m} }]-R\sum _{k}w_{k}}$

${\displaystyle \tau _{k}{\frac {dw_{k}(t)}{dt}}=-a_{k}[V_{\mathrm {m} }(t)-E_{\mathrm {m} }]-w_{k}+b_{k}\tau _{k}\sum _{f}\delta (t-t^{f})}$

куда ${\displaystyle \tau _{m}}$ постоянная времени мембраны, ш_k - текущий номер адаптации с индексом k, ${\displaystyle \tau _{k}}$ постоянная времени адаптационного тока ш_k, E_м потенциал покоя и т^ж - время срабатывания нейрона, а греческая дельта обозначает дельта-функцию Дирака. Когда напряжение достигает порога срабатывания, напряжение сбрасывается до значения V_р ниже порога срабатывания. Значение сброса - один из важных параметров модели. Самая простая модель адаптации имеет только одну переменную адаптации. ш и сумма по k удаляется.^[19]

Время всплесков и подпороговое напряжение моделей нейронов коры можно предсказать с помощью обобщенных моделей интеграции и запуска, таких как адаптивная модель интеграции и запуска, адаптивная экспоненциальная модель интеграции и запуска или модель спайк-отклика. В приведенном здесь примере адаптация реализуется с помощью динамического порога, который увеличивается после каждого всплеска.^[13][14]

Интегрируйте и активируйте нейроны с одной или несколькими адаптационными переменными, которые могут учитывать различные паттерны нейронального возбуждения в ответ на постоянную стимуляцию, включая адаптацию, взрыв и начальный взрыв.^[15][16][17] Более того, адаптивные нейроны с интеграцией и запуском с несколькими адаптационными переменными способны предсказывать время спайков кортикальных нейронов при зависящей от времени инъекции тока в сому.^[13][14]

Внешняя ссылка:

Адаптация и схемы стрельбы (Глава 6 учебника Neuronal Dynamics^[18])

Дефектный дефектный интеграл-и-огонь

Недавние достижения в вычислительном и теоретическом дробном исчислении привели к новой форме модели, называемой «интегрировать-и-активировать» с утечкой дробного порядка.^[20][21] Преимущество этой модели заключается в том, что она может улавливать эффекты адаптации с помощью одной переменной. Модель имеет следующий вид^[21]

${\displaystyle I(t)-{\frac {V_{\mathrm {m} }(t)}{R_{\mathrm {m} }}}=C_{\mathrm {m} }{\frac {d^{\alpha }V_{\mathrm {m} }(t)}{d^{\alpha }t}}}$

Как только напряжение достигает порогового значения, оно сбрасывается. Для учета адаптации нейронов в экспериментальных данных использовалась фракционная интеграция.^[20]

«Экспоненциальная интеграция и запуск» и «Адаптивная экспоненциальная интеграция и запуск»

Основная статья: Экспоненциальная интеграция и огонь

Экспериментальные доказательства, подтверждающие модель

Адаптивная экспоненциальная интеграция и запуск	Рекомендации
Подпороговое отношение тока к напряжению	[22]
Схемы срабатывания в ответ на ввод пошагового тока	[17]
Огнеупорность и адаптация	[23]

в экспоненциальная интеграция и огонь модель,^[24] Генерация всплесков экспоненциальна, согласно уравнению:

${\displaystyle {\frac {dV}{dt}}-{\frac {R}{\tau _{m}}}I(t)={\frac {1}{\tau _{m}}}[E_{m}-V+\Delta _{T}\exp \left({\frac {V-V_{T}}{\Delta _{T}}}\right)]}$.

куда ${\displaystyle V}$ - мембранный потенциал, ${\displaystyle V_{T}}$ - порог внутреннего мембранного потенциала, ${\displaystyle \tau _{m}}$ постоянная времени мембраны, ${\displaystyle E_{m}}$потенциал покоя, и ${\displaystyle \Delta _{T}}$ - резкость инициирования потенциала действия, обычно около 1 мВ для кортикальных пирамидных нейронов.^[22] Как только мембранный потенциал пересекает ${\displaystyle V_{T}}$, он расходится в бесконечность за конечное время.^[25] При численном моделировании интегрирование останавливается, если мембранный потенциал достигает произвольного порога (намного большего, чем ${\displaystyle V_{T}}$), при котором мембранный потенциал сбрасывается до значения V_р . Значение сброса напряжения V_р - один из важных параметров модели. Важно отметить, что правая часть приведенного выше уравнения содержит нелинейность, которую можно напрямую извлечь из экспериментальных данных.^[22] В этом смысле экспоненциальная нелинейность убедительно подтверждается экспериментальными данными.

в адаптивный экспоненциальный нейрон с интеграцией и запуском ^[23] Вышеупомянутая экспоненциальная нелинейность уравнения напряжения сочетается с адаптационной переменной w

${\displaystyle \tau _{m}{\frac {dV}{dt}}=RI(t)+[E_{m}-V+\Delta _{T}\exp \left({\frac {V-V_{T}}{\Delta _{T}}}\right)]-Rw}$

${\displaystyle \tau {\frac {dw(t)}{dt}}=-a[V_{\mathrm {m} }(t)-E_{\mathrm {m} }]-w+b\tau \delta (t-t^{f})}$

Схема срабатывания начального разрыва в ответ на входной ступенчатый ток, созданный с помощью адаптивной экспоненциальной модели интегрирования и зажигания. Также могут быть созданы другие схемы зажигания.^[17]

куда ш обозначает ток адаптации с временной шкалой ${\displaystyle \tau }$. Важными параметрами модели являются значение сброса напряжения. V_р, внутренний порог ${\displaystyle V_{T}}$, постоянные времени ${\displaystyle \tau }$ и ${\displaystyle \tau _{m}}$ а также параметры связи а и б. Адаптивная экспоненциальная модель интегрирования и зажигания наследует экспериментально полученную нелинейность напряжения. ^[22] экспоненциальной модели интегрирования и стрельбы. Но, выходя за рамки этой модели, она также может учитывать различные паттерны возбуждения нейронов в ответ на постоянную стимуляцию, включая адаптацию, взрыв и начальный взрыв.^[17]

Внешняя ссылка:

Адаптивная экспоненциальная интеграция и запуск (Глава 6.1 учебника Neuronal Dynamics^[18])

Стохастические модели мембранного напряжения и синхронизации всплесков

Модели в этой категории представляют собой обобщенные модели интеграции и исключения, которые включают определенный уровень стохастичности. Обнаружено, что в экспериментах корковые нейроны надежно реагируют на зависящие от времени входные данные, хотя и с небольшой степенью различий между одним испытанием и другим, если один и тот же стимул повторяется.^[26][27]Стохастичность нейронов имеет два важных источника. Во-первых, даже в очень контролируемом эксперименте, когда входной ток вводится непосредственно в сому, ионные каналы открываются и закрываются стохастически.^[28] и этот шум канала приводит к небольшой вариабельности точного значения мембранного потенциала и точной синхронизации выходных выбросов. Во-вторых, для нейрона, встроенного в корковую сеть, трудно контролировать точный ввод, потому что большинство входных данных поступает от ненаблюдаемых нейронов где-то еще в мозге.^[18]

Стохастичность была введена в модели нейронов пиков в двух фундаментально разных формах: либо (i) шумный вход Текущий добавляется к дифференциальному уравнению модели нейрона;^[29] или (ii) процесс генерация шипов шумная.^[30] В обоих случаях математическая теория может быть разработана для непрерывного времени, которое затем, при желании для использования в компьютерном моделировании, преобразуется в модель с дискретным временем.

Связь шума в моделях нейронов с изменчивостью цепочек спайков и нейронных кодов обсуждается в Нейронное кодирование и в главе 7 учебника Neuronal Dynamics.^[18]

Модель с шумным входом (диффузный шум)

Нейрон, встроенный в сеть, получает импульсный сигнал от других нейронов. Поскольку время прихода пиков не контролируется экспериментатором, их можно рассматривать как стохастические. Таким образом, (потенциально нелинейная) модель интегрирования и включения с нелинейностью f (v) получает два входа: вход ${\displaystyle I(t)}$ контролируется экспериментаторами и шумный входной ток ${\displaystyle I^{\rm {noise}}(t)}$ описывающий неконтролируемый фоновый ввод.

${\displaystyle \tau _{m}{\frac {dV}{dt}}=f(V)+RI(t)+RI^{\rm {noise}}(t)}$

Модель Штейна^[29] является частным случаем излучающего нейрона интеграции и зажигания и стационарного тока белого шума ${\displaystyle I^{\rm {noise}}(t)=\xi (t)}$ с нулевым средним и единичной дисперсией. В подпороговом режиме эти предположения приводят к уравнению Орнштейн-Уленбек процесс

${\displaystyle \tau _{m}{\frac {dV}{dt}}=[E_{m}-V]+RI(t)+R\xi (t)}$

Однако, в отличие от стандартного процесса Орнштейна-Уленбека, мембранное напряжение сбрасывается всякий раз, когда V достигает порога срабатывания. V_th.^[29] Расчет интервального распределения модели Орнштейна-Уленбека для постоянного входа с порогом приводит к первый раз проблема.^[29][31] Модель нейрона Стейна и ее варианты были использованы для соответствия распределению межспайковых интервалов последовательностей спайков от реальных нейронов при постоянном входном токе.^[31]

В математической литературе указанное выше уравнение процесса Орнштейна-Уленбека записывается в виде

${\displaystyle dV=[E_{m}-V+RI(t)]{\frac {dt}{\tau _{m}}}+\sigma dW}$

куда ${\displaystyle \sigma }$ - амплитуда входного шума и dW являются приращениями винеровского процесса. Для реализаций с дискретным временем и шагом по времени dt обновления напряжения^[18]

${\displaystyle \Delta V=[E_{m}-V+RI(t)]{\frac {\Delta t}{\tau _{m}}}+\sigma {\sqrt {\tau _{m}}}y}$

где y взят из гауссова распределения с нулевой средней единичной дисперсией. Напряжение сбрасывается, когда оно достигает порога срабатывания. V_th.

Модель с шумным входом также может использоваться в обобщенных моделях интеграции и возгорания. Например, экспоненциальная модель интегрировать и запустить с шумным входом читает

${\displaystyle \tau _{m}{\frac {dV}{dt}}=E_{m}-V+\Delta _{T}\exp \left({\frac {V-V_{T}}{\Delta _{T}}}\right)+RI(t)+R\xi (t)}$

Для постоянного детерминированного ввода ${\displaystyle I(t)=I_{0}}$ можно рассчитать среднюю скорострельность как функцию ${\displaystyle I_{0}}$.^[32] Это важно, потому что соотношение частота-ток (f-I-кривая) часто используется экспериментаторами для характеристики нейрона. Это также передаточная функция в

Негерметичная интеграция и запуск с шумным входом широко использовалась при анализе сетей нейронов с импульсами.^[33] Шумный вход также называется диффузным шумом, потому что он приводит к диффузии подпорогового мембранного потенциала по свободной от шума траектории (Johannesma,^[34] Диффузионные модели стохастической активности нейронов в нейронных сетях / Под ред. Caianelleo, Springer, 1968). Теория пиков нейронов с шумным входом рассматривается в главе 8.2 учебника. Нейронная динамика.^[18]

Внешняя ссылка:

Прибытие стохастического пика (Глава 8.2 учебника Neuronal Dynamics^[18])

Модель с шумным выходом (избегающий шум)

В детерминированных моделях интеграции и возгорания всплеск возникает, если мембранный потенциал V(т) достигает порога ${\displaystyle V_{th}}$. В моделях с шумным выходом строгий порог заменяется шумным следующим образом. В каждый момент времени t случайным образом генерируется всплеск с мгновенной стохастической интенсивностью или 'скорость побега' ^[18]

${\displaystyle \rho (t)=f(V(t)-V_{th})}$

что зависит от мгновенной разницы между мембранным напряжением V(т) и порог ${\displaystyle V_{th}}$.^[30] Обычный выбор для 'скорость побега' ${\displaystyle f}$ (что согласуется с биологическими данными^[13]) является

${\displaystyle f(V-V_{th})={\frac {1}{\tau _{0}}}\exp[\beta (V-V_{th}]}$

Генерация стохастических пиков (шумный выход) зависит от мгновенной разницы между мембранным потенциалом V (t) и порогом. Мембранный потенциал V модели Spike Response Model (SRM) имеет два вклада.^[35][36] Сначала входной ток I фильтруется первым фильтром k. Во-вторых, последовательность выбросов S (t) на выходе фильтруется вторым фильтром η и возвращается обратно. Результирующий мембранный потенциал V (t) используется для генерации всплесков на выходе с помощью стохастического процесса ρ (t) с интенсивностью, которая зависит от расстояния между мембранным потенциалом и порогом. Модель пикового отклика (SRM) тесно связана с Обобщенной линейной моделью (GLM).^[37][38]

куда ${\displaystyle \tau _{0}}$- постоянная времени, которая описывает, как быстро срабатывает импульс, когда мембранный потенциал достигает порогового значения и ${\displaystyle \beta }$ - параметр резкости. За ${\displaystyle \beta \to \infty }$ порог становится резким, и запуск импульса детерминированно происходит в момент, когда мембранный потенциал достигает порога снизу. Значение резкости, найденное в экспериментах^[13] является ${\displaystyle 1/\beta \approx 4mV}$ Это означает, что нейрональное возбуждение становится значимым, как только мембранный потенциал становится на несколько мВ ниже формального порога возбуждения.

Процесс скорости побега через мягкий порог рассматривается в главе 9 учебника. Нейрональная динамика.^[18]

Для моделей с дискретным временем всплеск генерируется с вероятностью

${\displaystyle P_{F}(t_{n})=F[V(t_{n})-V_{th}]}$

что зависит от мгновенной разницы между мембранным напряжением V вовремя ${\displaystyle t_{n}}$ и порог ${\displaystyle V_{th}}$.^[39] Функцию F часто принимают за стандартную сигмоидальную ${\displaystyle F(x)=0.5[1+\tanh(\gamma x)]}$ с параметром крутизны ${\displaystyle \gamma }$,^[30] аналогично динамике обновления в искусственных нейронных сетях. Но функциональная форма F также может быть получена из стохастической интенсивности ${\displaystyle f}$ в непрерывное время, представленное выше как ${\displaystyle F(y_{n})\approx 1-\exp[y_{n}\Delta t]}$ куда ${\displaystyle y_{n}=V(t_{n})-V_{th}}$ расстояние до порога.^[30]

Модели интеграции и запуска с выходным шумом можно использовать для прогнозирования PSTH реальных нейронов при произвольном зависящем от времени входном сигнале. ^[13] Для неадаптивных нейронов с интеграцией и запуском распределение интервалов при постоянной стимуляции может быть рассчитано из стационарных теория обновления. ^[18]

Внешняя ссылка

'мягкий порог' (Глава 9 учебника Нейрональная динамика.^[18])

Модель пикового отклика (SRM)

Экспериментальные доказательства, подтверждающие модель

Модель пикового отклика	Рекомендации
Допороговое напряжение для зависящего от времени входного тока	[14][40]
Время включения для зависящего от времени входного тока	[14][40]
Схемы срабатывания в ответ на ввод пошагового тока	[41][42]
Распределение интервала между спайками	[41][30]
Всплеск-постпотенциал	[14]
Порог огнеупорность и динамическая стрельба	[14][40]

основная статья: Модель пикового отклика

Модель пикового отклика (SRM) - это общая линейная модель для подпорогового мембранного напряжения в сочетании с нелинейным выходным шумовым процессом для генерации пиков.^[30][43][41] Напряжение мембраны V(т) в момент времени t

${\displaystyle V(t)=\sum _{f}\eta (t-t^{f})+\int _{0}^{\infty }\kappa (s)I(t-s)ds+V_{\mathrm {rest} }}$

куда т^ж - время срабатывания спайка f нейрона, V_отдых напряжение покоя при отсутствии входа, Его) входной ток в момент времени t-s и ${\displaystyle \kappa (s)}$ представляет собой линейный фильтр (также называемый ядром), который описывает вклад импульса входного тока в момент времени t-s в напряжение в момент времени t. Вклады в напряжение, вызванные всплеском во времени ${\displaystyle t^{f}}$ описываются тугоплавким ядром ${\displaystyle \eta (t-t^{f})}$. Особенно, ${\displaystyle \eta (t-t^{f})}$ описывает сброс после пика и динамику остаточного потенциала пика после пика. Следовательно, он выражает последствия рефрактерности и адаптации.^[30][14] Напряжение V (t) можно интерпретировать как результат интегрирования дифференциального уравнения модели с утечкой «интегрировать и воспламенить» в сочетании с произвольным числом переменных адаптации, запускаемых всплесками.^[15]

Возбуждение пиков является стохастическим и происходит со стохастической интенсивностью, зависящей от времени (мгновенная скорость)

${\displaystyle f(V-\vartheta (t))={\frac {1}{\tau _{0}}}\exp[\beta (V-\vartheta (t)]}$

с параметрами ${\displaystyle \tau _{0}}$ и ${\displaystyle \beta }$ и динамический порог ${\displaystyle \vartheta (t)}$ данный

${\displaystyle \vartheta (t)=\vartheta _{0}+\sum _{f}\theta _{1}(t-t^{f})}$

Здесь ${\displaystyle \vartheta _{0}}$ порог срабатывания неактивного нейрона и ${\displaystyle \theta _{1}(t-t^{f})}$ описывает повышение порога после всплеска во времени ${\displaystyle t^{f}}$.^[40][14] В случае фиксированного порога устанавливается ${\displaystyle \theta _{1}(t-t^{f})}$= 0. За ${\displaystyle \beta \to \infty }$ пороговый процесс детерминирован.^[18]

Временной ход фильтров ${\displaystyle \eta ,\kappa ,\theta _{1}}$ которые характеризуют модель спайк-отклика, могут быть непосредственно извлечены из экспериментальных данных.^[14] Благодаря оптимизированным параметрам SRM описывает временную динамику подпорогового мембранного напряжения для зависящего от времени входа с точностью до 2 мВ и может прогнозировать синхронизацию большинства всплесков на выходе с точностью до 4 мс. ^[40][14] SRM тесно связан с линейно-нелинейно-пуассоновский каскад модели (также называемые обобщенной линейной моделью).^[38] Оценка параметров вероятностных моделей нейронов, таких как SRM, с использованием методов, разработанных для обобщенных линейных моделей.^[44] обсуждается в главе 10 учебника Нейронная динамика.^[18]

Прибытие спайков вызывает суммирование постсинаптических потенциалов (красные линии). Если общее напряжение V достигает порогового значения (пунктирная синяя линия), инициируется всплеск (зеленый цвет), который также включает в себя остаточный импульс. Порог увеличивается после каждого всплеска. Постсинаптические потенциалы - это ответ на входящие всплески, в то время как пост-импульсный потенциал - это ответ на исходящие всплески.

Название Модель пикового отклика возникает потому, что в сети входной ток для нейрона i генерируется импульсами других нейронов, так что в случае сети уравнение напряжения становится

${\displaystyle V_{i}(t)=\sum _{f}\eta _{i}(t-t_{i}^{f})+\sum _{j=1}^{N}w_{ij}\sum _{f'}\epsilon _{ij}(t-t_{j}^{f'})+V_{\mathrm {rest} }}$

куда ${\displaystyle t_{j}^{f'}}$ время срабатывания нейрона j (т. е. его последовательность спайков), и ${\displaystyle \eta _{i}(t-t_{i}^{f})}$ описывает временной ход спайка и постпотенциала спайка для нейрона i, ${\displaystyle w_{ij}}$ и ${\displaystyle \epsilon _{ij}(t-t_{j}^{f'})}$ описать амплитуду и временной ход возбуждающего или тормозящего постсинаптический потенциал (PSP) вызвано всплеском ${\displaystyle t_{j}^{f'}}$ пресинаптического нейрона j. Курс времени ${\displaystyle \epsilon _{ij}(s)}$ PSP является результатом свертки постсинаптического тока ${\displaystyle I(t)}$ вызванный приходом пресинаптического спайка от нейрона j с мембранным фильтром ${\displaystyle \kappa (s)}$.^[18]

Внешняя ссылка:

Модель пикового отклика (Глава 6.4 учебника Нейронная динамика.^[18])

Модель спайкового отклика с побегом (Глава 9.1 учебника Нейронная динамика.^[18])

оценка параметров вероятностных моделей нейронов (Глава 10 учебника Нейронная динамика.^[18])

SRM0

В SRM0^[41][45][46] стохастическая модель нейрона, связанная с нестационарными нелинейными теория обновления и упрощение модели Spike Renose (SRM). Основное отличие от уравнения напряжения СУР введенных выше является то, что в перспективе, содержащий огнеупорное ядро ${\displaystyle \eta (s)}$ нет знака суммирования по прошлым всплескам: только последний всплеск (обозначается как время ${\displaystyle {\hat {t}}}$) имеет значение. Еще одно отличие состоит в том, что порог постоянный. Модель SRM0 может быть сформулирована в дискретном или непрерывном времени. Например, в непрерывном времени уравнение для одного нейрона имеет вид

${\displaystyle V(t)=\eta (t-{\hat {t}})+\int _{0}^{\infty }\kappa (s)I(t-s)ds+V_{\mathrm {rest} }}$

и сетевые уравнения SRM0 находятся^[41]

${\displaystyle V_{i}(t|{\hat {t}}_{i})=\eta _{i}(t-{\hat {t}}_{i})+\sum _{j}w_{ij}\sum _{f}\epsilon _{ij}(t-{\hat {t}}_{i},t-t^{f})+V_{\mathrm {rest} }}$

куда ${\displaystyle {\hat {t}}_{i}}$ это нейрон времени последнего срабатывания я. Обратите внимание, что динамика постсинаптического потенциала ${\displaystyle \epsilon _{ij}}$ также может зависеть от времени, прошедшего с момента последнего импульса нейрона i, чтобы описать изменение проводимости мембраны во время рефрактерности.^[45] Мгновенная скорость стрельбы (стохастическая интенсивность) равна

${\displaystyle f(V-\vartheta )={\frac {1}{\tau _{0}}}\exp[\beta (V-V_{th})]}$

куда ${\displaystyle V_{th}}$ фиксированный порог срабатывания. Таким образом, запуск импульса нейрона i зависит только от его входа и времени, прошедшего с того момента, как нейрон i выпустил свой последний импульс.

С SRM0, Распределение межимпульсных-интервал для постоянного ввода может быть математически связаны с формой огнеупорного ядра ${\displaystyle \eta }$ .^[30][41] Более того, стационарная зависимость частоты от тока может быть рассчитана на основе скорости утечки в сочетании с заводским ядром. ${\displaystyle \eta }$.^[30][41] При соответствующем выборе ядер SRM0 аппроксимирует динамику модели Ходжкина-Хаксли с высокой степенью точности.^[45] Более того, можно спрогнозировать реакцию PSTH на произвольный зависящий от времени ввод.^[41]

Модель Гальвеса – Лёхербаха

Трехмерная визуализация модели Гальвеса – Лехербаха для биологических нейронных сетей. Эта визуализация настроена для 4000 нейронов (4 слоя с одной популяцией тормозных нейронов и одной популяцией возбуждающих нейронов каждый) через 180 интервалов времени.

Основная статья: Модель Гальвеса – Лёхербаха

В Модель Гальвеса – Лёхербаха ^[47] это стохастический модель нейрона, тесно связанная с SRM Spike Response Model0 ^{[46] [41]} и дырявой модели «интегрировал и возгорал». Это по своей сути стохастический и, как и SRM0 связаны с зависящими от времени нелинейными теория обновления. Учитывая спецификации модели, вероятность того, что данный нейрон ${\displaystyle i}$ всплески в период времени ${\displaystyle t}$ может быть описан

${\displaystyle \mathop {\mathrm {Prob} } (X_{t}(i)=1|{\mathcal {F}}_{t-1})=\phi _{i}{\Biggl (}\sum _{j\in I}W_{j\rightarrow i}\sum _{s=L_{t}^{i}}^{t-1}g_{j}(t-s)X_{s}(j),~~~t-L_{t}^{i}{\Biggl )},}$

куда ${\displaystyle W_{j\rightarrow i}}$ это синаптический вес, описывающий влияние нейрона ${\displaystyle j}$ на нейрон ${\displaystyle i}$, ${\displaystyle g_{j}}$ выражает утечку, и ${\displaystyle L_{t}^{i}}$ предоставляет историю всплесков нейрона ${\displaystyle i}$ перед ${\displaystyle t}$, в соответствии с

${\displaystyle L_{t}^{i}={\text{sup}}\{s<t:X_{s}(i)=1\}.}$

Важно отметить, что вероятность спайка нейрона i зависит только от его спайкового входа (отфильтрованного ядром ${\displaystyle g_{j}}$ и взвешен с коэффициентом ${\displaystyle W_{j\to i}}$) и времени последнего всплеска объема производства (кратко ${\displaystyle t-L_{t}^{i}}$).

Дидактические игрушки модели мембранного напряжения

Модели в этой категории представляют собой сильно упрощенные игрушечные модели, которые качественно описывают мембранное напряжение как функцию входного сигнала. Они в основном используются в дидактических целях в обучении, но не считаются действительными моделями нейронов для крупномасштабного моделирования или подбора данных.

ФитцХью – Нагумо

Основная статья: Модель ФитцХью – Нагумо

Резкие упрощения Ходжкина-Хаксли были введены ФитцХью и Нагумо в 1961 и 1962 годах. Стремясь описать «регенеративное самовозбуждение» с помощью нелинейного мембранного напряжения с положительной обратной связью и восстановления с помощью линейного напряжения затвора с отрицательной обратной связью, они разработали описанную модель. к^[48]

${\displaystyle {\begin{array}{rcl}{\dfrac {dV}{dt}}&=&V-V^{3}/3-w+I_{\mathrm {ext} }\\\tau {\dfrac {dw}{dt}}&=&V-a-bw\end{array}}}$

где у нас снова есть мембранное напряжение и входной ток с более медленным общим напряжением затвора ш и экспериментально определенные параметры а = -0.7, б = 0.8, τ = 1/0.08. Хотя эта модель явно не выводится из биологии, она допускает упрощенную, немедленно доступную динамику, не являясь тривиальным упрощением.^[49] Экспериментальная поддержка слабая, но модель полезна как дидактический инструмент для представления динамики генерации спайков через фазовая плоскость анализ. См. Главу 7 в учебнике. Методы нейронного моделирования^[50]

Моррис – Лекар

Основная статья: Модель Морриса – Лекара

В 1981 году Моррис и Лекар объединили модели Ходжкина-Хаксли и ФитцХью-Нагумо в модель потенциалозависимого кальциевого канала с калиевым каналом с запаздыванием выпрямителя, представленной

${\displaystyle {\begin{array}{rcl}C{\dfrac {dV}{dt}}&=&-I_{\mathrm {ion} }(V,w)+I\\{\dfrac {dw}{dt}}&=&\phi \cdot {\dfrac {w_{\infty }-w}{\tau _{w}}}\end{array}}}$

куда ${\displaystyle I_{\mathrm {ion} }(V,w)={\bar {g}}_{\mathrm {Ca} }m_{\infty }\cdot (V-V_{\mathrm {Ca} })+{\bar {g}}_{\mathrm {K} }w\cdot (V-V_{\mathrm {K} })+{\bar {g}}_{\mathrm {L} }\cdot (V-V_{\mathrm {L} })}$.^[8] Экспериментальная поддержка модели слабая, но модель полезна как дидактический инструмент для представления динамики генерации спайков через фазовая плоскость анализ. См. Главу 7^[51] в учебнике Методы нейронного моделирования.^[50]

Двумерная модель нейрона, очень похожая на модель Морриса-Лекара, может быть получена пошагово, начиная с модели Ходжкина-Хаксли. См. Главу 4.2 в учебнике «Нейрональная динамика».^[18]

Внешняя ссылка:

Сведение к двум измерениям (Глава 4.2. Учебника Нейронная динамика.^[18])

Хиндмарш – Роуз

Основная статья: Модель Хиндмарша – Роуза

Основываясь на модели ФитцХью – Нагумо, Хиндмарш и Роуз предложили в 1984 г.^[52] модель нейронной активности, описываемая тремя связанными дифференциальными уравнениями первого порядка:

${\displaystyle {\begin{array}{rcl}{\dfrac {dx}{dt}}&=&y+3x^{2}-x^{3}-z+I\\{\dfrac {dy}{dt}}&=&1-5x^{2}-y\\{\dfrac {dz}{dt}}&=&r\cdot (4(x+{\tfrac {8}{5}})-z)\end{array}}}$

с р² = Икс² + у² + z², и р ≈ 10⁻² таким образом z только переменная изменяется очень медленно. Эта дополнительная математическая сложность допускает большое разнообразие динамических характеристик мембранного потенциала, описываемых Икс переменная модели, включающая хаотическую динамику. Это делает модель нейрона Хиндмарша – Роуза очень полезной, поскольку, будучи все еще простой, позволяет качественно описать множество различных паттернов возбуждения потенциала действия, в частности взрывных, наблюдаемых в экспериментах. Тем не менее, это остается игрушечной моделью и не соответствует экспериментальным данным. Он широко используется в качестве эталонной модели для динамики разрыва.^[52]

Тета-модель и квадратичная интеграция-и-огонь.

В тета-модель, или Ermentrout – Kopell канонический Модель типа I математически эквивалентна квадратичной модели интегрирования и включения, которая, в свою очередь, является приближением к экспоненциальной модели интегрирования и включения и модели Ходжкина-Хаксли. Это называется канонической моделью, потому что это одна из общих моделей для постоянного входа, близкого к точке бифуркации, что означает близость к переходу от бесшумного к повторяющемуся срабатыванию.^[53][54]

Стандартная формулировка тета-модели:^[18][53][54]

${\displaystyle {\frac {d\theta (t)}{dt}}=(I-I_{0})[1+\cos(\theta )]+[1-\cos(\theta )]}$

Уравнение для квадратичной модели интегрирования и возгорания (см. Главу 5.3 в учебнике Нейронная динамика ^[18]))

${\displaystyle \tau _{\mathrm {m} }{\frac {dV_{\mathrm {m} }(t)}{dt}}=(I-I_{0})R+[V_{\mathrm {m} }(t)-E_{\mathrm {m} }][V_{\mathrm {m} }(t)-V_{\mathrm {T} }]}$

Эквивалентность тета-модели и квадратичной интеграции и включения рассматривается, например, в главе 4.1.2.2 «Модели нейронных импульсов».^[1]

Для входа I (t), который изменяется со временем или находится далеко от точки бифуркации, предпочтительнее работать с экспоненциальной моделью интеграции и запуска (если кто-то хочет остаться в классе одномерных моделей нейронов), потому что реальные нейроны демонстрируют нелинейность экспоненциальной модели интегрирования и активации.^[22]

Внешняя ссылка:

Модели нейронов типа I и типа II (Глава 4.4 учебника Нейронная динамика.^[18])

Квадратичная модель интеграции и стрельбы (Глава 5.3 учебника Нейронная динамика.^[18])

Модели нейронов, кодирующие сенсорный ввод и стимул

Модели в этой категории были получены в результате экспериментов с естественной стимуляцией, такой как свет, звук, прикосновение или запах. В этих экспериментах характер спайков, возникающий в результате каждого предъявления стимула, варьируется от испытания к испытанию, но усредненный ответ от нескольких испытаний часто сходится к четкому образцу. Следовательно, модели в этой категории генерируют вероятностную взаимосвязь между входным стимулом и возникновением всплесков. Важно отметить, что записанные нейроны часто расположены на нескольких этапах обработки после сенсорных нейронов, так что эти модели суммируют эффекты последовательности этапов обработки в компактной форме.

Неоднородная модель пуассоновского процесса (Зиберт)

Зиберт^[55][56] смоделировал паттерн возбуждения спайков нейрона, используя неоднородный Пуассоновский процесс модель, после экспериментов с участием слуховой системы.^[55][56] По словам Зиберта, вероятность всплеска на временном интервале ${\displaystyle [t,t+\Delta _{t}]}$ пропорциональна неотрицательной функции ${\displaystyle g[s(t)]}$, куда ${\displaystyle s(t)}$ это необработанный стимул:

${\displaystyle P_{spike}(t\in [t',t'+\Delta _{t}])=\Delta _{t}\cdot g[s(t)]}$

Зиберт считал несколько функций ${\displaystyle g[s(t)]}$, включая ${\displaystyle g[s(t)]\propto s^{2}(t)}$ для слабых стимулов.

Основное преимущество модели Зиберта - ее простота. Недостатком модели является неспособность правильно отразить следующие явления:

• Временное усиление возбуждающей активности нейронов в ответ на ступенчатый стимул.
• Насыщение скорострельности.
• Значения межспайкового интервала-гистограмма на коротких интервалах значений (близких к нулю).

Эти недостатки устраняются с помощью модели точечного процесса, зависящей от возраста, и модели Маркова с двумя состояниями.^[57][58][59]

Рефрактерность и возрастная модель точечного процесса

Берри и Мейстер^[60] изучал рефрактерность нейронов с помощью стохастической модели, которая предсказывает спайки как произведение двух членов: функции f (s (t)), которая зависит от зависящего от времени стимула s (t), и функции восстановления ${\displaystyle w(t-{\hat {t}})}$ это зависит от времени с момента последнего всплеска

${\displaystyle \rho (t)=f(s(t))w(t-{\hat {t}})}$

Модель также называют неоднородный процесс с марковским интервалом (IMI).^[61] Подобные модели уже много лет используются в слуховой нейробиологии.^{[62][63] [64]} Поскольку модель хранит в памяти время последнего всплеска, она не является пуассоновской и относится к классу моделей восстановления, зависящего от времени.^[18] Он тесно связан с моделью SRM0 с экспоненциальная скорость ухода.^[18] Важно отметить, что можно подогнать параметры модели точечного процесса, зависящей от возраста, чтобы описать не только отклик PSTH, но и статистику межспайковых интервалов.^[61][62][65]

Линейно-нелинейная модель каскада Пуассона и GLM

Основная статья: Модель линейно-нелинейно-пуассоновского каскада

В Линейно-нелинейная модель Пуассона представляет собой каскад процесса линейной фильтрации, за которым следует шаг генерации нелинейных пиков.^[66] В случае, если выбросы на выходе имеют обратную связь, через процесс линейной фильтрации, мы приходим к модели, известной в нейробиологии как Обобщенная линейная модель (GLM).^[38][44] GLM математически эквивалентен модели Spike Response (SRM) с убегающим шумом; но в то время как в SRM внутренние переменные интерпретируются как мембранный потенциал и порог срабатывания, в GLM внутренние переменные представляют собой абстрактные величины, которые суммируют чистый эффект входных данных (и недавних всплесков выхода) до того, как на заключительном этапе будут сгенерированы всплески.^[18][38]

внешняя ссылка:

Модели кодирования и декодирования в системной нейробиологии (Глава 11.2 учебника Нейронная динамика.^[18])

Модель Маркова с двумя состояниями (Носсенсон и Мессер)

Модель пикового нейрона Носсенсона и Мессера^[57][58][59] создает вероятность того, что нейрон вызовет спайк в зависимости от внешнего или фармакологического стимула.^[57][58][59] Модель состоит из каскада модели рецепторного слоя и модели нейрона с импульсами, как показано на рис. 4. Связь между внешним стимулом и вероятностью выброса осуществляется в два этапа. Во-первых, модель рецепторной клетки преобразует исходный внешний стимул. с концентрацией нейротрансмиттера, то модель пикового нейрона связывает между концентрацией нейротрансмиттера и частотой срабатывания (вероятностью пика). Таким образом, модель импульсного нейрона сама по себе зависит от концентрации нейротрансмиттера на входной стадии.^[57][58][59]

Рис. 4: Блок-схема высокого уровня рецепторного слоя и модели нейрона от Nossenson & Messer.^[57][59]

Рис. 5. Прогноз скорости стрельбы в ответ на импульсный стимул, представленный моделью Nossenson & Messer.^[57][59]

Важной особенностью этой модели является предсказание паттерна скорости возбуждения нейронов, которая фиксирует, используя небольшое количество свободных параметров, характерный ответ нейронов на импульс стимула, подчеркнутый краями, как показано на рис. 5. Скорость возбуждения идентифицируется как как нормализованная вероятность срабатывания нервного импульса и как величина, пропорциональная току нейромедиаторов, выделяемых клеткой. Выражение для скорострельности принимает следующий вид:

${\displaystyle R_{fire}(t)={\frac {P_{spike}(t;\Delta _{t})}{\Delta _{t}}}=[y(t)+R_{0}]\cdot P_{0}(t)}$

куда,

• P0 - вероятность того, что нейрон будет "вооружен" и готов к срабатыванию. Он задается следующим дифференциальным уравнением:

${\displaystyle {\dot {P}}_{0}=-[y(t)+R_{0}+R_{1}]\cdot P_{0}(t)+R_{1}}$

P0 обычно можно вычислить рекурсивно с использованием метода Эйлера, но в случае импульса стимула он дает простое выражение в замкнутой форме.^[57][67]

• y (t) является входом модели и интерпретируется как концентрация нейротрансмиттера в окружающей клетке (в большинстве случаев глутамат). Для внешнего стимула его можно оценить с помощью модели рецепторного слоя:

${\displaystyle y(t)\simeq g_{gain}\cdot \langle s^{2}(t)\rangle }$ , с ${\displaystyle \langle s^{2}(t)\rangle }$ краткое временное среднее значение мощности стимула (выраженное в ваттах или другой энергии в единицу времени).

• R0 соответствует собственной скорости спонтанной активации нейрона.
• R1 - скорость выхода нейрона из рефрактерного состояния.

Другие прогнозы этой модели включают:

1) Усредненный потенциал вызванного ответа (ERP) из-за популяции многих нейронов в нефильтрованных измерениях напоминает частоту возбуждения.^[59]

2) Изменение напряжения активности из-за активности нескольких нейронов напоминает скорость возбуждения (также известную как мощность Multi-Unit-Activity или MUA).^[58][59]

3) Распределение вероятностей между интервалами всплесков принимает форму функции, подобной гамма-распределению.^[57][67]

Экспериментальные доказательства, подтверждающие модель Носсенсона и Мессера^[57][58][59]

Собственность модели Носсенсона и Мессера	Рекомендации	Описание экспериментальных данных
Форма темпа стрельбы в ответ на импульс слухового раздражителя	[68][69][70][71][72]	Скорость стрельбы такая же, как на рис.5.
Форма темпа стрельбы в ответ на импульс визуального стимула	[73][74][75][76]	Скорость стрельбы такая же, как на рис.5.
Форма скорости стрельбы в ответ на импульс обонятельного стимула	[77]	Скорость стрельбы такая же, как на рис.5.
Форма скорости стрельбы в ответ на сомато-сенсорный раздражитель	[78]	Скорость стрельбы такая же, как на рис.5.
Изменение скорости возбуждения в ответ на применение нейромедиатора (в основном глутамата)	[79][80]	Изменение скорости стрельбы в ответ на приложение нейротрансмиттера (глутамат)
Квадратная зависимость между давлением слухового стимула и скоростью стрельбы	[81]	Квадратная зависимость между давлением звукового стимула и скоростью стрельбы (- линейная зависимость в квадрате давления (мощности)).
Квадратная зависимость между электрическим полем визуального стимула (в вольтах) и скоростью стрельбы	[74]	Квадратная зависимость между электрическим полем визуального стимула (вольт) - линейная зависимость между визуальным стимулом Мощность и скорострельность.
Форма статистики интервала между спайками (ISI)	[82]	Форма ISI напоминает гамма-функцию.
ERP напоминает скорость стрельбы в нефильтрованных измерениях	[83]	Форма усредненного потенциала вызванной реакции на стимул напоминает скорость стрельбы (рис. 5).
Мощность MUA напоминает скорострельность	[59][84]	Форма эмпирической дисперсии внеклеточных измерений в ответ на импульс стимула напоминает частоту возбуждения (рис. 5).

Фармакологические модели нейронов входного стимула

Модели этой категории позволяют делать прогнозы для экспериментов с фармакологической стимуляцией.

Синаптическая передача (Кох и Сегев)

Смотрите также: Нейротрансмиссия

Согласно модели Коха и Сегева,^[8] Ответ нейрона на отдельные нейротрансмиттеры можно смоделировать как расширение классической модели Ходжкина-Хаксли как со стандартными, так и с нестандартными кинетическими токами. Четыре нейротрансмиттера в первую очередь влияют на ЦНС. AMPA / каинатные рецепторы быстрые возбуждающий посредники пока Рецепторы NMDA опосредуют значительно более медленные токи. Быстрый тормозящий токи проходят ГАМК_А рецепторы, пока ГАМК_B рецепторы посредничество вторичным грамм-белковые калиевые каналы. Этот диапазон посредничества дает следующую текущую динамику:

• ${\displaystyle I_{\mathrm {AMPA} }(t,V)={\bar {g}}_{\mathrm {AMPA} }\cdot [O]\cdot (V(t)-E_{\mathrm {AMPA} })}$
• ${\displaystyle I_{\mathrm {NMDA} }(t,V)={\bar {g}}_{\mathrm {NMDA} }\cdot B(V)\cdot [O]\cdot (V(t)-E_{\mathrm {NMDA} })}$
• ${\displaystyle I_{\mathrm {GABA_{A}} }(t,V)={\bar {g}}_{\mathrm {GABA_{A}} }\cdot ([O_{1}]+[O_{2}])\cdot (V(t)-E_{\mathrm {Cl} })}$
• ${\displaystyle I_{\mathrm {GABA_{B}} }(t,V)={\bar {g}}_{\mathrm {GABA_{B}} }\cdot {\tfrac {[G]^{n}}{[G]^{n}+K_{\mathrm {d} }}}\cdot (V(t)-E_{\mathrm {K} })}$

куда грамм это максимальный^[2][8] проводимость (около 1S ) и E - равновесный потенциал данного иона или передатчика (AMDA, NMDA, Cl, или же K ), пока [О] описывает долю открытых рецепторов. Для NMDA существует значительный эффект магниевый блок это зависит от сигмоидально на концентрацию внутриклеточного магния путем B(V). Для ГАМК_B, [грамм] это концентрация грамм-белок и K_d описывает диссоциацию грамм в привязке к калиевым воротам.

Динамика этой более сложной модели была хорошо изучена экспериментально и дает важные результаты с точки зрения очень быстрого синаптическое потенцирование и депрессия, то есть быстрое краткосрочное обучение.

Стохастик модель Носсенсона и Мессера переводит концентрацию нейротрансмиттера на входной стадии в вероятность высвобождения нейромедиатора на выходной стадии.^[57][58][59] Более подробное описание этой модели см. Два состояния Марковской модели сечения над.

Модель нейрона HTM

Модель нейрона HTM была разработана Джефф Хокинс и исследователи в Numenta и основан на теории под названием Иерархическая временная память, первоначально описанный в книге Об интеллекте. Он основан на нейробиология и физиология и взаимодействие пирамидные нейроны в неокортекс человеческого мозга.

Сравнивая искусственная нейронная сеть (A), биологический нейрон (B) и нейрон HTM (C).

Искусственная нейронная сеть (ИНС)	Неокортикальный пирамидный нейрон (биологический нейрон)	Модель HTM Neuron
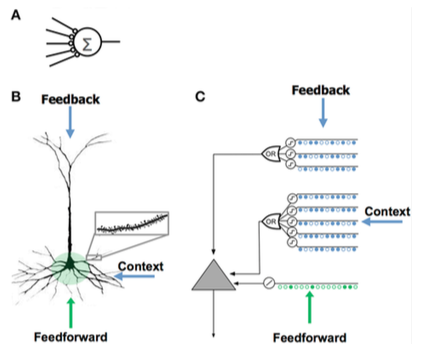
- Мало синапсов - Без дендритов - Суммарный ввод x весов - Обучает, изменяя веса синапсов	- Тысячи синапсов на дендритах - Активные дендриты: клетка распознает сотни уникальных паттернов - Совместная активация набора синапсов на дендритном сегменте вызывает спайк NMDA и деполяризацию сомы. - Источники ввода в ячейку: Прямые входы, которые образуют синапсы проксимальнее сомы и напрямую приводят к потенциалам действия Спайки NMDA генерируются в более дистальных базальных Апикальные дендриты, деполяризующие сому (обычно недостаточно для создания потенциала соматического действия) - Учится, выращивая новые синапсы	- Вдохновленный пирамидными клетками 2/3 и 5 слоев неокортекса - Тысячи синапсов - Активные дендриты: клетка распознает сотни уникальных паттернов - Моделирует дендриты и шипы NMDA с каждым массивом совпадающих детекторов, имеющим набор синапсов - Учится, моделируя рост новых синапсов

Приложения

основная статья: мозг-компьютерные интерфейсы

Модели нейронных импульсов используются в различных приложениях, которые требуют кодирования или декодирования из цепочек импульсов нейронов в контексте нейропротезирования и мозг-компьютерные интерфейсы Такие как протез сетчатки ^[6][85]:^[86][87] или искусственный контроль конечностей и ощущения. ^[88][89][90] Приложения не являются частью этой статьи; для получения дополнительной информации по этой теме обратитесь к основной статье.

Связь между искусственными и биологическими моделями нейронов

Самая простая модель нейрона состоит из входа с некоторыми синаптический вес вектор и функция активации или же функция передачи внутри нейрона, определяющего выход. Это основная структура, используемая для искусственных нейронов, которые в нейронная сеть часто выглядит как

${\displaystyle y_{i}=\phi \left(\sum _{j}w_{ij}x_{j}\right)}$

куда у_я это результат я й нейрон, Икс_j это j-й входной сигнал нейрона, ш_ij это синаптический вес (или сила связи) между нейронами я и j, и φ это функция активации. Хотя эта модель успешно применяется в приложениях для машинного обучения, она не подходит для реальных (биологических) нейронов, поскольку в ней отсутствует зависимость ввода и вывода от времени.

Когда вход включается в момент времени t и после этого остается постоянным, биологические нейроны излучают последовательность импульсов. Важно отметить, что эта последовательность пиков не является регулярной, а демонстрирует временную структуру, характеризующуюся адаптацией, разрывом или начальным разрывом, за которым следует регулярный всплеск. Обобщенная модель интеграции и запуска, такая как модель Adaptive Exponential Integrate and Fire, модель Spike Response или (линейная) адаптивная модель интеграции и запуска, способна уловить эти паттерны возбуждения нейронов.^[15][16][17]

Более того, нейронный вход в мозг зависит от времени. Входные данные, зависящие от времени, преобразуются сложными линейными и нелинейными фильтрами в цепочку всплесков на выходе. Опять же, модель Spike Response или адаптивная модель интегрирования и запуска позволяют прогнозировать последовательность всплесков на выходе для произвольного зависящего от времени входа,^[13][14] тогда как искусственный нейрон или простой негерметичный интегрируй и запускай - нет.

Если мы возьмем модель Ходкгина-Хаксли в качестве отправной точки, обобщенные модели интегрирования и исключения могут быть получены систематически с помощью пошаговой процедуры упрощения. Это было явно показано для экспоненциальная интеграция и огонь^[24] модель и Модель спайк-отклика.^[45]

В случае моделирования биологического нейрона вместо абстракций, таких как «вес» и «передаточная функция», используются физические аналоги. Нейрон заполнен и окружен водой, содержащей ионы, несущие электрический заряд. Нейрон связан изолирующей клеточной мембраной и может поддерживать концентрацию заряженных ионов с обеих сторон, которая определяет емкость C_м. Возбуждение нейрона включает движение ионов в клетку, которое происходит, когда нейротрансмиттеры причина ионные каналы на клеточной мембране, чтобы открыть. Мы описываем это физически зависящим от времени Текущий я(т). С этим происходят изменения в Напряжение, или разность электрической потенциальной энергии между клеткой и ее окружением, что иногда приводит к скачок напряжения называется потенциал действия который проходит по длине клетки и запускает высвобождение других нейромедиаторов. Напряжение, в таком случае, представляет собой интересующую величину и определяется выражением V_м(т).^[10]

Если входной ток постоянный, большинство нейронов после некоторого времени адаптации или первоначального взрыва излучают регулярную серию импульсов. Частота штатных срабатываний при постоянном токе я описывается соотношением частота-ток, которое соответствует передаточной функции ${\displaystyle \phi }$ искусственных нейронных сетей. Точно так же для всех моделей нейронов с импульсами передаточная функция ${\displaystyle \phi }$ можно рассчитать численно (или аналитически).

Теория кабеля и модели отсеков

Смотрите также: Теория кабеля

Все вышеперечисленные детерминированные модели являются моделями точечных нейронов, поскольку они не учитывают пространственную структуру нейрона. Однако дендрит способствует преобразованию входных данных в выходные.^[91][50] Модели точечных нейронов пригодны для описания в трех случаях. (i) Если входной ток вводится непосредственно в сому. (ii) Если синаптический вход поступает преимущественно в сому или близко к ней (размер закрытия определяется по шкале длины ${\displaystyle \lambda }$ представлен ниже. (iii) Если синапс попадает куда-нибудь на дендрит, но дендрит полностью линейный. В последнем случае кабель действует как линейный фильтр; эти свойства линейного фильтра могут быть включены в формулировку обобщенных моделей интегрирования и пожаротушения, таких как Модель пикового отклика.

Свойства фильтра можно вычислить из уравнение кабеля.

Рассмотрим клеточную мембрану в виде цилиндрического кабеля. Положение кабеля обозначено x, а напряжение на клеточной мембране - V. Кабель характеризуется продольным сопротивлением. ${\displaystyle r_{l}}$ на единицу длины и сопротивление мембраны ${\displaystyle r_{m}}$ . Если все линейно, напряжение изменяется как функция времени.

${\displaystyle {\frac {r_{m}}{r_{l}}}{\frac {\partial ^{2}V}{\partial x^{2}}}=c_{m}r_{m}{\frac {\partial V}{\partial t}}+V}$

(19)

Введем масштаб длины ${\displaystyle \lambda ^{2}={r_{m}}/{r_{l}}}$ слева и постоянная времени ${\displaystyle \tau =c_{m}r_{m}}$ на правой стороне. В уравнение кабеля теперь можно записать в его, пожалуй, самой известной форме:

${\displaystyle \lambda ^{2}{\frac {\partial ^{2}V}{\partial x^{2}}}=\tau {\frac {\partial V}{\partial t}}+V}$

(20)

Вышеприведенное уравнение кабеля действительно для одиночного цилиндрического кабеля.

Теория линейного кабеля описывает дендритная ветвь нейрона как цилиндрической структуры, подвергающейся регулярному паттерну бифуркация, как ветви на дереве. Для одного цилиндра или всего дерева статическая входная проводимость в основании (где дерево встречается с телом ячейки или любой такой границей) определяется как

${\displaystyle G_{in}={\frac {G_{\infty }\tanh(L)+G_{L}}{1+(G_{L}/G_{\infty })\tanh(L)}}}$,

куда L - электротоническая длина цилиндра, которая зависит от его длины, диаметра и сопротивления. Простой рекурсивный алгоритм линейно масштабируется с количеством ветвей и может использоваться для вычисления эффективной проводимости дерева. Это дается

${\displaystyle \,\!G_{D}=G_{m}A_{D}\tanh(L_{D})/L_{D}}$

куда А_D = πld это общая площадь дерева полной длины л, и L_D - его полная электротоническая длина. Для целого нейрона, в котором проводимость тела клетки равна грамм_S а проводимость мембраны на единицу площади равна грамм_мкр = грамм_м / А, находим полную проводимость нейрона грамм_N за п дендритных деревьев путем сложения проводимости всех деревьев и сомы, полученной

${\displaystyle G_{N}=G_{S}+\sum _{j=1}^{n}A_{D_{j}}F_{dga_{j}}}$,

где мы можем найти общий поправочный коэффициент F_dga экспериментально, отмечая грамм_D = грамм_мкрА_DF_dga.

Модель линейного кабеля делает ряд упрощений для получения закрытых аналитических результатов, а именно, что дендритная ветвь должна разветвляться уменьшающимися парами по фиксированному образцу и что дендриты являются линейными. Компартментная модель^[50] допускает любую желаемую топологию дерева с произвольными ветвями и длинами, а также произвольными нелинейностями. По сути, это дискретная вычислительная реализация нелинейных дендритов.

Каждый отдельный кусок или отделение дендрита моделируется прямым цилиндром произвольной длины. л и диаметр d который соединяется с фиксированным сопротивлением с любым количеством разветвленных цилиндров. Определим коэффициент проводимости я-й цилиндр как B_я = грамм_я / грамм_∞, куда ${\displaystyle G_{\infty }={\tfrac {\pi d^{3/2}}{2{\sqrt {R_{i}R_{m}}}}}}$ и р_я сопротивление между текущим отсеком и следующим. Мы получаем серию уравнений для коэффициентов проводимости внутри и вне отсека, внося поправки в нормальную динамику. B_из,я = B_{в,я + 1}, так как

• ${\displaystyle B_{\mathrm {out} ,i}={\frac {B_{\mathrm {in} ,i+1}(d_{i+1}/d_{i})^{3/2}}{\sqrt {R_{\mathrm {m} ,i+1}/R_{\mathrm {m} ,i}}}}}$
• ${\displaystyle B_{\mathrm {in} ,i}={\frac {B_{\mathrm {out} ,i}+\tanh X_{i}}{1+B_{\mathrm {out} ,i}\tanh X_{i}}}}$
• ${\displaystyle B_{\mathrm {out,par} }={\frac {B_{\mathrm {in,dau1} }(d_{\mathrm {dau1} }/d_{\mathrm {par} })^{3/2}}{\sqrt {R_{\mathrm {m,dau1} }/R_{\mathrm {m,par} }}}}+{\frac {B_{\mathrm {in,dau2} }(d_{\mathrm {dau2} }/d_{\mathrm {par} })^{3/2}}{\sqrt {R_{\mathrm {m,dau2} }/R_{\mathrm {m,par} }}}}+\ldots }$

где последнее уравнение имеет дело с родители и дочери в филиалах и ${\displaystyle X_{i}={\tfrac {l_{i}{\sqrt {4R_{i}}}}{\sqrt {d_{i}R_{m}}}}}$. Мы можем повторять эти уравнения по дереву, пока не получим точку, в которой дендриты соединяются с телом клетки (сома), где коэффициент проводимости равен B_{в, стержень}. Тогда наша общая проводимость нейрона для статического входа определяется выражением

${\displaystyle G_{N}={\frac {A_{\mathrm {soma} }}{R_{\mathrm {m,soma} }}}+\sum _{j}B_{\mathrm {in,stem} ,j}G_{\infty ,j}}$.

Важно отметить, что статический ввод - это особый случай. В биологии входные данные зависят от времени. Более того, дендриты не всегда линейны.

Компартментные модели позволяют учитывать нелинейности через ионные каналы, расположенные в произвольных местах вдоль дендритов.^[91][92] Для статических входов иногда можно уменьшить количество отсеков (увеличить скорость вычислений) и при этом сохранить основные электрические характеристики.^[93]

Смотрите также: Модель с несколькими отсеками

Предположения о роли нейрона в более широком контексте принципа работы мозга

Схема обнаружения энергии на основе нейротрансмиттеров

Схема обнаружения энергии на основе нейротрансмиттеров^[59][67] предполагает, что нервная ткань химически выполняет процедуру обнаружения, подобную радару.

Рис. 6. Схема биологического нейронного обнаружения, предложенная Nossenson et al.^[59][67]

Как показано на рис.6, ключевая идея гипотезы состоит в том, чтобы учесть концентрацию нейротрансмиттера, генерацию нейротрансмиттера и скорость удаления нейромедиатора как важные величины при выполнении задачи обнаружения, при этом относясь к измеренным электрическим потенциалам как к побочному эффекту, который только в определенных условия совпадают с функциональным назначением каждой ступени. Схема обнаружения похожа на радароподобное «обнаружение энергии», потому что она включает в себя возведение сигнала в квадрат, временное суммирование и механизм переключения порогов, как и детектор энергии, но также включает блок, который выделяет края стимула и переменную длину памяти ( переменная память). Согласно этой гипотезе, физиологическим эквивалентом статистики энергетического теста является концентрация нейротрансмиттера, а скорость возбуждения соответствует току нейротрансмиттера. Преимущество этой интерпретации состоит в том, что она приводит к единому последовательному объяснению, которое позволяет связать электрофизиологические измерения, биохимические измерения и психофизические результаты.

Доказательства, рассмотренные в^[59][67] предполагают следующую связь между функциональностью и гистологической классификацией:

1. Возведение в квадрат стимула, вероятно, будет выполняться рецепторными клетками.
2. Подчеркивание краев стимула и передача сигнала осуществляется нейронами.
3. Накопление нейромедиаторов во времени осуществляется глиальными клетками. Кратковременное накопление нейротрансмиттеров также может происходить в некоторых типах нейронов.
4. Логическое переключение осуществляется глиальными клетками и является результатом превышения порогового уровня концентрации нейромедиатора. Это превышение порога также сопровождается изменением скорости утечки нейромедиатора.
5. Физическое переключение движения «все или без движения» происходит из-за мышечных клеток и является результатом превышения определенного порога концентрации нейромедиаторов в окружении мышц.

Обратите внимание, что, хотя электрофизиологические сигналы на рисунке 6 часто похожи на функциональный сигнал (мощность сигнала / концентрация нейротрансмиттера / мышечная сила), есть некоторые этапы, на которых электрическое наблюдение отличается от функционального назначения соответствующего этапа. В частности, Nossenson et al. предположили, что пересечение порога глии имеет совершенно другое функциональное действие по сравнению с излучаемым электрофизиологическим сигналом, и что последний может быть только побочным эффектом разрыва глии.

Общие комментарии относительно современной перспективы научных и инженерных моделей

• Вышеупомянутые модели все еще являются идеализациями. Необходимо внести поправки на увеличенную площадь поверхности мембраны, обусловленную многочисленными дендритными шипами, температурами, значительно более высокими, чем экспериментальные данные при комнатной температуре, и неоднородностью внутренней структуры клетки.^[8] Некоторые наблюдаемые эффекты не укладываются в некоторые из этих моделей. Например, циклическое изменение температуры (с минимальным чистым повышением температуры) клеточной мембраны во время распространения потенциала действия несовместимо с моделями, которые полагаются на моделирование мембраны как сопротивления, которое должно рассеивать энергию при протекании через нее тока. Переходное утолщение клеточной мембраны во время распространения потенциала действия также не предсказывается этими моделями, равно как и изменение емкости и скачка напряжения, возникающие в результате этого утолщения, не включены в эти модели. Действие некоторых анестетиков, таких как инертные газы, также проблематично для этих моделей. Новые модели, такие как солитонная модель пытаются объяснить эти явления, но они менее развиты, чем более старые модели, и еще не получили широкого применения.
• Современные взгляды на роль научной модели предполагают, что «все модели ошибочны, но некоторые полезны» (Box and Draper, 1987, Gribbin, 2009; Paninski et al., 2009).
• Недавнее предположение предполагает, что каждый нейрон может функционировать как набор независимых пороговых единиц. Предполагается, что нейрон может быть анизотропно активирован по происхождению сигналов, поступающих к мембране, через его дендритные деревья. Также было предложено, чтобы форма волны спайка зависела от происхождения стимула.^[94]

внешняя ссылка

• Нейрональная динамика: от отдельных нейронов до сетей и моделей познания (В. Герстнер, В. Кистлер, Р. Науд, Л. Панински, Издательство Кембриджского университета, 2014 г.).^[18] Особенно, Главы 6 - 10, онлайн-версия html.
• Пиковые модели нейронов^[1] (В. Герстнер и В. Кистлер, Cambridge University Press, 2002)

Смотрите также

• Связывающий нейрон
• Байесовские подходы к функции мозга
• Интерфейсы мозг-компьютер
• Принцип свободной энергии
• Модели нейронных вычислений
• Нейронное кодирование
• Нейронные колебания
• Количественные модели потенциала действия
• Пиковая нейронная сеть

Рекомендации

1. Герстнер В., Кистлер В. М. (2002). Модели нейронов с импульсами: отдельные нейроны, популяции, пластичность. Кембридж, Великобритания: Издательство Кембриджского университета. ISBN  0-511-07817-X. OCLC  57417395.
2. Ходжкин А.Л., Хаксли А.Ф. (август 1952 г.). «Количественное описание мембранного тока и его применение к проводимости и возбуждению в нерве». Журнал физиологии. 117 (4): 500–44. Дои:10.1113 / jphysiol.1952.sp004764. ЧВК  1392413. PMID  12991237.
3. Ходжкин А.Л., Хаксли А.Ф., Кац Б. (апрель 1952 г.). «Измерение вольт-амперных отношений в мембране гигантского аксона Лолиго». Журнал физиологии. 116 (4): 424–48. Дои:10.1113 / jphysiol.1952.sp004716. ЧВК  1392219. PMID  14946712.
4. Ходжкин А.Л., Хаксли А.Ф. (апрель 1952 г.). «Токи, переносимые ионами натрия и калия через мембрану гигантского аксона Лолиго». Журнал физиологии. 116 (4): 449–72. Дои:10.1113 / jphysiol.1952.sp004717. ЧВК  1392213. PMID  14946713.
5. Ходжкин А.Л., Хаксли А.Ф. (апрель 1952 г.). «Компоненты проводимости мембраны в гигантском аксоне Лолиго». Журнал физиологии. 116 (4): 473–96. Дои:10.1113 / jphysiol.1952.sp004718. ЧВК  1392209. PMID  14946714.
6. Mathieson K, Loudin J, Goetz G, Huie P, Wang L, Kamins TI и др. (Июнь 2012 г.). «Фотоэлектрический протез сетчатки с высокой плотностью пикселей». Природа Фотоника. 6 (6): 391–397. Bibcode:2012НаФо ... 6..391M. Дои:10.1038 / nphoton.2012.104. ЧВК  3462820. PMID  23049619.
7. Эбботт Л.Ф. (1999). "Введение Лапиком модели нейрона" интегрируй и стреляй "(1907)" (PDF). Бюллетень исследований мозга. 50 (5–6): 303–4. Дои:10.1016 / S0361-9230 (99) 00161-6. PMID  10643408. S2CID  46170924. Архивировано из оригинал (PDF) 13 июня 2007 г.
8. Кох C, Сегев I (1999). Методы нейронного моделирования: от ионов к сетям (2-е изд.). Кембридж, Массачусетс: MIT Press. п. 687. ISBN  978-0-262-11231-4. Архивировано из оригинал на 2011-07-07. Получено 2013-01-10.
9. Брунель, Николас (2000-05-01). «Динамика слабосвязанных сетей возбуждающих и тормозящих нейронов». Журнал вычислительной неврологии. 8 (3): 183–208. Дои:10.1023 / А: 1008925309027. ISSN  1573-6873.
10. Cejnar P, Vyšata O, Kukal J, Beránek M, Vališ M, Procházka A (апрель 2020 г.). «Простая модель возбуждающего и тормозящего нейрона с переключателем между конденсаторами и биологически объясненными всеми частями позволяет вводить хаотические колебания, зависящие от модели огня». Научные отчеты. 10 (1): 7353. Bibcode:2020НатСР..10.7353С. Дои:10.1038 / s41598-020-63834-7. ЧВК  7192907. PMID  32355185.
11. Fuortes MG, Mantegazzini F (июль 1962 г.). «Интерпретация повторяющихся возбуждений нервных клеток». Журнал общей физиологии. 45 (6): 1163–79. Дои:10.1085 / jgp.45.6.1163. ЧВК  2195242. PMID  13895926.
12. La Camera G, Rauch A, Lüscher HR, Senn W, Fusi S (октябрь 2004 г.). «Минимальные модели адаптированного нейронального ответа на входные токи, подобные in vivo». Нейронные вычисления. 16 (10): 2101–24. Дои:10.1162/0899766041732468. PMID  15333209. S2CID  1428381.
13. Жоливет Р., Раух А., Люшер Х. Р., Герстнер В. (август 2006 г.). «Прогнозирование времени спайков пирамидных нейронов неокортекса с помощью простых пороговых моделей». Журнал вычислительной неврологии. 21 (1): 35–49. Дои:10.1007 / s10827-006-7074-5. PMID  16633938. S2CID  8911457.
14. Поццорини С., Науд Р., Менси С., Герстнер В. (июль 2013 г.). «Темпоральное отбеливание за счет степенной адаптации нейронов неокортекса». Природа Неврология. 16 (7): 942–8. Дои:10.1038 / № 3431. PMID  23749146. S2CID  1873019.
15. Герстнер В., ван Хеммен Дж. Л., Коуэн Дж. Д. (ноябрь 1996 г.). «Что имеет значение в блокировке нейронов?». Нейронные вычисления. 8 (8): 1653–76. Дои:10.1162 / neco.1996.8.8.1653. PMID  8888612. S2CID  1301248.
16. Ижикевич Е.М. (ноябрь 2003 г.). «Простая модель импульсных нейронов». IEEE-транзакции в нейронных сетях. 14 (6): 1569–72. Дои:10.1109 / TNN.2003.820440. PMID  18244602.
17. Науд Р., Марсиль Н., Клопат С., Герстнер В. (ноябрь 2008 г.). «Шаблоны стрельбы в адаптивной экспоненциальной модели интеграции и стрельбы». Биологическая кибернетика. 99 (4–5): 335–47. Дои:10.1007 / s00422-008-0264-7. ЧВК  2798047. PMID  19011922.
18. Вульфрам Герстнер В., Кистлер В. М., Науд Р., Панински Л. (24 июля 2014 г.). Нейрональная динамика: от отдельных нейронов к сетям и моделям познания. Кембридж, Соединенное Королевство. ISBN  978-1-107-06083-8. OCLC  861774542.
19. Ричардсон М.Дж., Брунель Н., Хаким В. (май 2003 г.). «От подпорогового до скорострельного резонанса». Журнал нейрофизиологии. 89 (5): 2538–54. Дои:10.1152 / ян.00955.2002. PMID  12611957.
20. Лундстрем Б. Н., Хиггс М. Х., Испания В. Дж., Фэрхолл А. Л. (ноябрь 2008 г.). «Фракционная дифференцировка пирамидными нейронами неокортекса». Природа Неврология. 11 (11): 1335–42. Дои:10.1038 / № 2212. ЧВК  2596753. PMID  18931665.
21. Teka W, Marinov TM, Santamaria F (март 2014 г.). «Адаптация синхронизации нейронных спайков описана с помощью модели дробной утечки интегрируй и зажигай». PLOS вычислительная биология. 10 (3): e1003526. Bibcode:2014PLSCB..10E3526T. Дои:10.1371 / journal.pcbi.1003526. ЧВК  3967934. PMID  24675903.
22. Бадель Л., Лефорт С., Бретт Р., Петерсен С.Ч., Герстнер В, Ричардсон MJ (февраль 2008 г.). «Динамические кривые I-V являются надежными предикторами естественных кривых напряжения пирамидных нейронов». Журнал нейрофизиологии. 99 (2): 656–66. CiteSeerX  10.1.1.129.504. Дои:10.1152 / ян.01107.2007. PMID  18057107.
23. Бретт Р., Герстнер В. (ноябрь 2005 г.). «Адаптивная экспоненциальная модель интеграции и запуска как эффективное описание нейронной активности». Журнал нейрофизиологии. 94 (5): 3637–42. Дои:10.1152 / ян.00686.2005. PMID  16014787.
24. Fourcaud-Trocmé N, Hansel D, van Vreeswijk C, Brunel N (декабрь 2003 г.). «Как механизмы генерации спайков определяют ответ нейронов на колебания входных сигналов». Журнал неврологии. 23 (37): 11628–40. Дои:10.1523 / JNEUROSCI.23-37-11628.2003. ЧВК  6740955. PMID  14684865.
25. Остожич С., Брунель Н., Хаким В. (август 2009 г.). «Как связь, фоновая активность и синаптические свойства формируют взаимную корреляцию между шипами». Журнал неврологии. 29 (33): 10234–53. Дои:10.1523 / JNEUROSCI.1275-09.2009. ЧВК  6665800. PMID  19692598.
26. Bryant HL, Segundo JP (сентябрь 1976 г.). «Инициирование всплеска трансмембранным током: анализ белого шума». Журнал физиологии. 260 (2): 279–314. Дои:10.1113 / jphysiol.1976.sp011516. ЧВК  1309092. PMID  978519.
27. Майнен З.Ф., Сейновски Т.Дж. (июнь 1995 г.). «Надежность спайков в нейронах неокортекса». Наука. 268 (5216): 1503–6. Дои:10.1126 / science.7770778. PMID  7770778.
28. Манвани А., Кох С. (ноябрь 1999 г.). «Обнаружение и оценка сигналов в зашумленной кабельной структуре, I: источники нейронного шума». Нейронные вычисления. 11 (8): 1797–829. Дои:10.1162/089976699300015972. PMID  10578033. S2CID  12298894.
29. Штейн РБ (март 1965 г.). "ТЕОРЕТИЧЕСКИЙ АНАЛИЗ НЕЙРОННОЙ ВАРИАБЕЛЬНОСТИ". Биофизический журнал. 5 (2): 173–94. Bibcode:1965BpJ ..... 5..173S. Дои:10.1016 / с0006-3495 (65) 86709-1. ЧВК  1367716. PMID  14268952.
30. Герстнер В., ван Хеммен Дж. Л. (январь 1992 г.). «Ассоциативная память в сети« шипящих »нейронов». Сеть: вычисления в нейронных системах. 3 (2): 139–164. Дои:10.1088 / 0954-898X_3_2_004. ISSN  0954-898X.
31. Дитлевсен С., Лански П. (январь 2005 г.). «Оценка входных параметров в нейрональной модели Орнштейна-Уленбека». Физический обзор. E, Статистическая, нелинейная физика и физика мягкой материи. 71 (1 Пт 1): 011907. Bibcode:2005PhRvE..71a1907D. Дои:10.1103 / PhysRevE.71.011907. PMID  15697630.
32. Ричардсон MJ (август 2007 г.). «Отклик скорости возбуждения линейных и нелинейных нейронов с интеграцией и запуском на модулированный синаптический привод на основе тока и проводимости». Физический обзор. E, Статистическая, нелинейная физика и физика мягкой материи. 76 (2 Пт 1): 021919. Bibcode:2007PhRvE..76b1919R. Дои:10.1103 / PhysRevE.76.021919. PMID  17930077.
33. Брунель Н (1 мая 2000 г.). «Динамика слабо связанных сетей возбуждающих и тормозных нейронов». Журнал вычислительной неврологии. 8 (3): 183–208. Дои:10.1023 / А: 1008925309027. PMID  10809012. S2CID  1849650.
34. Йоханнесма, П.И.М. (1968). Каянелло, Э. Р. (ред.). Диффузионные модели стохастической активности нейронов. Springer. С. 116–144.
35. Герстнер, Вульфрам; Хеммен, Дж. Лео ван (1992-01-01). «Ассоциативная память в сети« шипящих »нейронов». Сеть: вычисления в нейронных системах. 3 (2): 139–164. Дои:10.1088 / 0954-898X_3_2_004. ISSN  0954-898X.
36. Герстнер, Вульфрам (1 января 1995). «Временная структура активности в моделях нейронных сетей». Физический обзор E. 51 (1): 738–758. Дои:10.1103 / PhysRevE.51.738.
37. Трукколо, Уилсон; Eden, Uri T .; Товарищи, Мэтью Р .; Донохью, Джон П .; Браун, Эмери Н. (01.02.2005). «Структура точечного процесса для связи активности нейронных импульсов с историей всплесков, нейронным ансамблем и внешними ковариантными эффектами». Журнал нейрофизиологии. 93 (2): 1074–1089. Дои:10.1152 / ян.00697.2004. ISSN  0022-3077.
38. Подушка Дж. В., Шленс Дж., Панински Л., Шер А., Литке А. М., Чичильнский Е. Ю., Симончелли Е. П. (август 2008 г.). «Пространственно-временные корреляции и визуальная сигнализация в полной нейронной популяции». Природа. 454 (7207): 995–9. Дои:10.1038 / природа07140. ЧВК  2684455. PMID  18650810.
39. Вайс Т.Ф. (ноябрь 1966 г.). «Модель периферической слуховой системы». Кибернетик. 3 (4): 153–75. Дои:10.1007 / BF00290252. PMID  5982096.
40. Жоливет Р., Раух А., Люшер Х. Р., Герстнер В. (август 2006 г.). «Прогнозирование времени спайков пирамидных нейронов неокортекса с помощью простых пороговых моделей». Журнал вычислительной неврологии. 21 (1): 35–49. Дои:10.1007 / s10827-006-7074-5. PMID  16633938.
41. Герстнер В. (январь 2000 г.). «Динамика популяции импульсных нейронов: быстрые переходные процессы, асинхронные состояния и блокировка». Нейронные вычисления. 12 (1): 43–89. Дои:10.1162/089976600300015899. PMID  10636933.
42. Науд Р., Герстнер В. (2012-10-04). Sporns O (ред.). «Кодирование и декодирование с адаптирующимися нейронами: популяционный подход к временной гистограмме перистимулов». PLoS вычислительная биология. 8 (10): e1002711. Дои:10.1371 / journal.pcbi.1002711. ЧВК  3464223. PMID  23055914.
43. Герстнер В., Ритц Р., ван Хеммен Дж. Л. (октябрь 1993 г.). «Почему всплески? Хеббийское обучение и извлечение разрешенных во времени моделей возбуждения». Биологическая кибернетика. 69 (5–6): 503–515. Дои:10.1007 / BF00199450. ISSN  0340-1200.
44. Панински Л. (ноябрь 2004 г.). «Оценка максимального правдоподобия каскадных точечных моделей нейронного кодирования». Сеть. 15 (4): 243–62. Дои:10.1088 / 0954-898X_15_4_002. PMID  15600233.
45. Кистлер В. М., Герстнер В., Хеммен Дж. Л. (01.07.1997). «Сведение уравнений Ходжкина-Хаксли к модели с одним переменным порога». Нейронные вычисления. 9 (5): 1015–1045. Дои:10.1162 / neco.1997.9.5.1015. ISSN  0899-7667.
46. Герстнер В. (январь 1995 г.). «Временная структура активности в моделях нейронных сетей». Физический обзор. E, Статистическая физика, плазма, жидкости и смежные междисциплинарные темы. 51 (1): 738–758. Дои:10.1103 / PhysRevE.51.738. PMID  9962697.
47. Гальвес А, Лёхербах Э (2013). «Бесконечные системы взаимодействующих цепей с памятью переменной длины - стохастическая модель для биологических нейронных сетей». Журнал статистической физики. 151 (5): 896–921. arXiv:1212.5505. Bibcode:2013JSP ... 151..896G. Дои:10.1007 / s10955-013-0733-9. S2CID  119161279.
48. Фитцхью Р. (июль 1961 г.). «Импульсы и физиологические состояния в теоретических моделях нервной мембраны». Биофизический журнал. 1 (6): 445–66. Bibcode:1961BpJ ..... 1..445F. Дои:10.1016 / S0006-3495 (61) 86902-6. ЧВК  1366333. PMID  19431309.
49. ФитцХью Р., Ижикевич Э. (2006). «Модель ФитцХью-Нагумо». Scholarpedia. 1 (9): 1349. Bibcode:2006SchpJ ... 1.1349I. Дои:10.4249 / scholarpedia.1349.
50. Методы нейронного моделирования: от ионов к сетям (02 изд.). [Место публикации не указано]: Mit Press. 2003 г. ISBN  0-262-51713-2. OCLC  947133821.
51. Ринзель Дж, Эрментроут Б. "Глава 7: Анализ нервной возбудимости и колебаний". В Сегеве I, Кохе С. (ред.). Методы нейронного моделирования. п. 251. ISBN  978-0262517133.
52. Хиндмарш Дж, Корнелиус П. (01.10.2005). «Разработка модели шиповника на лопуху». Взрыв. МИРОВАЯ НАУЧНАЯ. С. 3–18. Дои:10.1142/9789812703231_0001. ISBN  978-981-256-506-8.
53. Эрментраут Г., Копелл Н. (1986). «Параболический взрыв в возбуждаемой системе в сочетании с медленными колебаниями». Журнал SIAM по прикладной математике. 46 (2): 233–253. Дои:10.1137/0146017. ISSN  0036-1399.
54. Ermentrout B (июль 1996 г.). «Мембраны типа I, кривые возврата фазы и синхронность». Нейронные вычисления. 8 (5): 979–1001. Дои:10.1162 / neco.1996.8.5.979. PMID  8697231. S2CID  17168880.
55. Зиберт WM (1970-05-01). «Частотная дискриминация в слуховой системе: место или механизмы периодичности?». Труды IEEE. 58 (5): 723–730. Дои:10.1109 / PROC.1970.7727. ISSN  0018-9219.
56. Зиберт WM (июнь 1965 г.). «Некоторые следствия стохастического поведения первичных слуховых нейронов». Кибернетик. 2 (5): 206–15. Дои:10.1007 / BF00306416. PMID  5839007. S2CID  9744183.
57. Носсенсон Н., Мессер Х (2010). «Моделирование паттерна срабатывания нейрона с использованием двухуровневой цепи Маркова». 2010 IEEE Sensor Array and Multichannel Signal Processing Workshop.. Дои:10.1109 / SAM.2010.5606761. ISBN  978-1-4244-8978-7. S2CID  10973225.
58. Носсенсон Н., Мессер Х (апрель 2012 г.). «Оптимальное последовательное обнаружение стимулов из многокомпонентных записей, сделанных в густонаселенных областях мозга». Нейронные вычисления. 24 (4): 895–938. Дои:10.1162 / NECO_a_00257. PMID  22168560. S2CID  16994688.
59. Носсенсон Н., Магал Н., Мессер Х (2016). «Обнаружение стимулов от активности нескольких нейронов: эмпирическое исследование и теоретические выводы». Нейрокомпьютеры 174 (2016): 822-837. 174: 822–837. Дои:10.1016 / j.neucom.2015.10.007.
60. Берри MJ, Meister M (март 1998 г.). «Огнеупорность и нейронная точности». Журнал неврологии. 18 (6): 2200–11. Дои:10.1523 / JNEUROSCI.18-06-02200.1998. ЧВК  6792934. PMID  9482804.
61. Kass RE, Ventura V (август 2001 г.). «Вероятностная модель шипованного поезда». Нейронные вычисления. 13 (8): 1713–20. Дои:10.1162/08997660152469314. PMID  11506667. S2CID  9909632.
62. Gaumond, R.P; Мольнар, С. Э .; Ким, Д. О. (сентябрь 1982 г.). «Зависимость от стимула и восстановления вероятности разряда спайков нервного волокна улитки кошки». Журнал нейрофизиологии. 48 (3): 856–873. Дои:10.1152 / jn.1982.48.3.856. ISSN  0022-3077.
63. Миллер, Майкл I .; Марк, Кевин Э. (1992-07-01). «Статистическое исследование паттернов разряда кохлеарного нерва в ответ на сложные речевые стимулы». Журнал акустического общества Америки. 92 (1): 202–209. Дои:10.1121/1.404284. ISSN  0001-4966.
64. Джонсон Д.Х., Свами А. (август 1983 г.). «Передача сигналов по разряду волокон слухового нерва». Журнал акустического общества Америки. 74 (2): 493–501. Bibcode:1983ASAJ ... 74..493J. Дои:10.1121/1.389815. PMID  6311884.
65. Джонсон, Дон Х .; Свами, Анантрам (август 1983 г.). «Передача сигналов по разряду волокон слухового нерва». Журнал акустического общества Америки. 74 (2): 493–501. Дои:10.1121/1.389815. ISSN  0001-4966.
66. Чичильнский, Э. Дж. (01.02.2001). «Простой анализ белого шума световых ответов нейронов». Сеть: вычисления в нейронных системах. 12 (2): 199–213. Дои:10.1080/713663221. ISSN  0954-898X.
67. Носсенсон Н. (2013). Обнаружение наличия стимула по нейрофизиологическим сигналам на основе моделей (PDF). Библиотека точных наук и инженерии им. Неймана, Тель-Авивский университет: докторская диссертация, Тель-Авивский университет.
68. Келер С.Д., Прадхан С., Манис П.Б., Шор С.Е. (февраль 2011 г.). «Соматосенсорные входы изменяют синхронизацию слуховых спайков в основных клетках дорсального кохлеарного ядра». Европейский журнал нейробиологии. 33 (3): 409–20. Дои:10.1111 / j.1460-9568.2010.07547.x. ЧВК  3059071. PMID  21198989.
69. Reches A, Gutfreund Y (февраль 2008 г.). «Стимул-специфические адаптации в системе управления взором сипухи». Журнал неврологии. 28 (6): 1523–33. Дои:10.1523 / JNEUROSCI.3785-07.2008. ЧВК  6671572. PMID  18256273.
70. Ван X, Лу Т., Снайдер Р.К., Лян Л. (май 2005 г.). «Устойчивое возбуждение в слуховой коре, вызванное предпочтительными стимулами». Природа. 435 (7040): 341–6. Bibcode:2005 Натур.435..341W. Дои:10.1038 / природа03565. PMID  15902257. S2CID  4312195.
71. Табернер AM, Либерман MC (январь 2005 г.). «Свойства ответа отдельных волокон слухового нерва у мыши». Журнал нейрофизиологии. 93 (1): 557–69. Дои:10.1152 / jn.00574.2004. PMID  15456804.
72. Хенневин Э., Харс Б., Махо С., Блох V (1995-07-01). «Обработка усвоенной информации в парадоксальном сне: актуальность для памяти». Поведенческие исследования мозга. Функция сна. 69 (1–2): 125–35. Дои:10.1016 / 0166-4328 (95) 00013-J. PMID  7546303. S2CID  4034082.
73. Родик RW (декабрь 1965 г.). «Количественный анализ реакции ганглиозных клеток сетчатки кошки на зрительные раздражители». Исследование зрения. 5 (11): 583–601. Дои:10.1016/0042-6989(65)90033-7. PMID  5862581.
74. Энрот-Кугель С., Ленни П. (июнь 1975 г.). «Контроль разряда ганглиозных клеток сетчатки с помощью окружения рецептивного поля». Журнал физиологии. 247 (3): 551–78. Дои:10.1113 / jphysiol.1975.sp010947. ЧВК  1309488. PMID  1142301.
75. Энрот-Кугелл С., Шепли Р.М. (сентябрь 1973 г.). «Адаптация и динамика ганглиозных клеток сетчатки кошки». Журнал физиологии. 233 (2): 271–309. Дои:10.1113 / jphysiol.1973.sp010308. ЧВК  1350567. PMID  4747229.
76. Сагдуллаев Б.Т., Макколл М.А. (01.09.2005). «Размер и интенсивность стимула изменяют фундаментальные свойства рецептивного поля ганглиозных клеток сетчатки мыши in vivo». Визуальная неврология. 22 (5): 649–59. Дои:10.1017 / S0952523805225142. PMID  16332276.
77. Нагель К.И., Уилсон Р.И. (февраль 2011 г.). «Биофизические механизмы, лежащие в основе динамики нейронов обонятельных рецепторов». Природа Неврология. 14 (2): 208–16. Дои:10.1038 / № 2725. ЧВК  3030680. PMID  21217763.
78. Tommerdahl M, Delemos KA, Whitsel BL, Favorov OV, Metz CB (июль 1999 г.). «Ответ передней теменной коры на трепетание кожи по сравнению с вибрацией». Журнал нейрофизиологии. 82 (1): 16–33. Дои:10.1152 / jn.1999.82.1.16. PMID  10400931. S2CID  14729461.
79. Хадипур Никтараш А., Шахиди Г.А. (2004-03-01). «Влияние активности внутренней петли бледного шара-педункулопонтина на передачу колебательной активности субталамического ядра-внешнего бледного шара-водителя ритма к коре». Журнал вычислительной неврологии. 16 (2): 113–27. Дои:10.1023 / B: JCNS.0000014105.87625.5f. PMID  14758061. S2CID  20728260.
80. Яманака Й, Китамура Н., Шинохара Х, Такахаши К., Сибуя I. (январь 2013 г.). «Глутамат вызывает возбуждение за счет активации каинатных рецепторов в нейронах добавочной доли цыпленка». Журнал сравнительной физиологии. A, Нейроэтология, сенсорная, нервная и поведенческая физиология. 199 (1): 35–43. Дои:10.1007 / s00359-012-0766-6. PMID  23064516. S2CID  15527085.
81. Мюллер М., Робертсон Д., Йейтс Г.К. (сентябрь 1991 г.). «Скоростные функции первичных волокон слухового нерва: доказательства квадратичного поведения всех категорий волокон у морских свинок». Слуховые исследования. 55 (1): 50–6. Дои:10.1016 / 0378-5955 (91) 90091-М. PMID  1752794. S2CID  40343090.
82. Джонсон DH, Кианг Нью-Йорк (июль 1976 г.). «Анализ разрядов, зарегистрированных одновременно от пар волокон слухового нерва». Биофизический журнал. 16 (7): 719–34. Bibcode:1976BpJ .... 16..719J. Дои:10.1016 / с0006-3495 (76) 85724-4. ЧВК  1334896. PMID  938715.
83. Буллок TH (1 января 1997 г.). «Сравнительная физиология акустических и родственных им центральных анализаторов». Acta Oto-Laryngologica. Дополнение. 532 (sup532): 13–21. Дои:10.3109/00016489709126139. PMID  9442839.
84. Гольштейн С.Б., Бухвальд Дж. С., Швафель Дж. А. (ноябрь 1969 г.). «Прогрессивные изменения в паттернах слуховой реакции на повторяющийся тон при нормальном бодрствовании и параличе». Исследование мозга. 16 (1): 133–48. Дои:10.1016/0006-8993(69)90090-0. PMID  5348845.
85. Риццо Дж. Ф. (июнь 2011 г.). «Обновленная информация об исследовании протезов сетчатки: Бостонский проект по имплантации сетчатки». Журнал нейроофтальмологии. 31 (2): 160–8. Дои:10.1097 / wno.0b013e31821eb79e. PMID  21593628. S2CID  17213342.
86. Петерман М.С., Мехенти Н.З., Бильбао К.В., Ли С.Дж., Ленг Т., Нооланди Дж. И др. (Ноябрь 2003 г.). «Искусственный чип синапсов: гибкий интерфейс сетчатки, основанный на направленном росте клеток сетчатки и стимуляции нейромедиаторов». Искусственные органы. 27 (11): 975–85. Дои:10.1046 / j.1525-1594.2003.07307.x. PMID  14616516.
87. Иеззи Р., Финлейсон П., Сюй И, Катрагадда Р. (01.09.2009). «Нейронные интерфейсы на основе микрофлюидных нейротрансмиттеров для протеза сетчатки». Ежегодная международная конференция IEEE Engineering in Medicine and Biology Society. IEEE Engineering in Medicine and Biology Society. Ежегодная международная конференция. 2009: 4563–5. Дои:10.1109 / IEMBS.2009.5332694. PMID  19963838. S2CID  2751102.
88. Йошида К., Фарина Д., Акай М., Дженсен В. (01.03.2010). «Многоканальные внутривенные и внутримышечные методы для многоканальной записи и использования в активных протезах». Труды IEEE. 98 (3): 432–449. Дои:10.1109 / JPROC.2009.2038613. ISSN  0018-9219. S2CID  23631268.
89. Bruns TM, Wagenaar JB, Bauman MJ, Gaunt RA, Weber DJ (апрель 2013 г.). «Контроль функциональной электростимуляции задних конечностей в реальном времени с использованием обратной связи по записям ганглиев задних корешков». Журнал нейронной инженерии. 10 (2): 026020. Bibcode:2013JNEng..10b6020B. Дои:10.1088/1741-2560/10/2/026020. ЧВК  3640462. PMID  23503062.
90. «BrainGate - Дом». braingate2.org. 2015-12-04. Получено 2016-04-06.
91. Hay E, Hill S, Schürmann F, Markram H, Segev I (июль 2011 г.). «Модели пирамидных клеток неокортикального слоя 5b, обладающие широким спектром дендритных и перисоматических активных свойств». PLoS вычислительная биология. 7 (7): e1002107. Bibcode:2011PLSCB ... 7E2107H. Дои:10.1371 / journal.pcbi.1002107. ЧВК  3145650. PMID  21829333.
92. Markram H, Muller E, Ramaswamy S, Reimann MW, Abdellah M, Sanchez CA и др. (Октябрь 2015 г.). «Реконструкция и моделирование микросхем неокортекса». Клетка. 163 (2): 456–92. Дои:10.1016 / j.cell.2015.09.029. PMID  26451489. S2CID  14466831.
93. Форрест, доктор медицины (апрель 2015 г.). «Моделирование действия алкоголя на детальной модели нейрона Пуркинье и более простой суррогатной модели, которая работает в> 400 раз быстрее». BMC Neuroscience. 16 (27): 27. Дои:10.1186 / s12868-015-0162-6. ЧВК  4417229. PMID  25928094.
94. Сарди С., Варди Р., Шейнин А., Голденталь А., Кантер И. (декабрь 2017 г.). «Новые типы экспериментов показывают, что нейрон функционирует как несколько независимых пороговых единиц». Научные отчеты. 7 (1): 18036. Bibcode:2017НатСР ... 718036S. Дои:10.1038 / s41598-017-18363-1. ЧВК  5740076. PMID  29269849.