Метрика Лукашика – Кармовского - Łukaszyk–Karmowski metric

В математика, то Метрика Лукашика – Кармовского это функция определение расстояние между двумя случайные переменные или два случайные векторы.^[1][2] Эта функция не метрика поскольку это не удовлетворяет идентичность неразличимых состояние метрики, то есть для двух одинаковых аргументов ее значение больше нуля. Концепция названа в честь Шимона Лукашика и Войцеха Кармовского.

Непрерывные случайные величины

Метрика Лукашика – Кармовского D между двумя непрерывными независимыми случайные переменные Икс и Y определяется как:

${\displaystyle D(X,Y)=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }|x-y|f(x)g(y)\,dx\,dy}$

куда ж(Икс) и грамм(y) - функции плотности вероятности Икс и Y соответственно.

Легко показать, что такие метрики выше не удовлетворяют идентичность неразличимых условие, необходимое для выполнения метрика из метрическое пространство. Фактически они удовлетворяют этому условию если и только если оба аргумента Икс, Y определенные события описываются Дельта Дирака плотность функции распределения вероятностей. В таком случае:

${\displaystyle D_{\delta \delta }(X,Y)=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }|x-y|\delta (x-\mu _{x})\delta (y-\mu _{y})\,dx\,dy=|\mu _{x}-\mu _{y}|}$

метрика Лукашика – Кармовского просто превращается в метрику между ожидаемые значения ${\displaystyle \mu _{x}}$, ${\displaystyle \mu _{y}}$ переменных Икс и Y и очевидно:

${\displaystyle D_{\delta \delta }(X,X)=|\mu _{x}-\mu _{x}|=0.}$

Для всех остальных настоящий случаи, однако:

${\displaystyle D\left(X,X\right)>0.\,}$

Метрика Лукашика – Кармовского удовлетворяет оставшимся неотрицательность и симметрия условия метрика непосредственно из его определения (симметрия модуля), а также субаддитивность /неравенство треугольника условие:

${\displaystyle {\begin{aligned}&{}D(X,Z)=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }|x-z|f(x)h(z)\,dx\,dz\ =\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }|x-z|f(x)h(z)\,dx\,dz\int _{-\infty }^{\infty }g(y)dy\ \\&{}=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }|(x-y)+(y-z)|f(x)g(y)h(z)\,dx\,dy\,dz\ \\&{}\leq \int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }(|x-y|+|y-z|)f(x)g(y)h(z)\,dx\,dy\,dz\ \\&{}=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }|x-y|f(x)g(y)h(z)\,dx\,dy\,dz\ +\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }|y-z|f(x)g(y)h(z)\,dx\,dy\,dz\ \\&{}=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }|x-y|f(x)g(y)\,dx\,dy\ +\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }|y-z|g(y)h(z)\,dy\,dz\ \\&{}=D(X,Y)+D(Y,Z)\end{aligned}}}$

Таким образом

${\displaystyle D(X,Z)\leq D(X,Y)+D(Y,Z).\,}$

L – K-метрика между двумя случайными величинами Икс и Y имея нормальные распределения и то же самое стандартное отклонение ${\displaystyle \sigma =0,\sigma =0.2,\sigma =0.4,\sigma =0.6,\sigma =0.8,\sigma =1}$ (начиная с нижней кривой). ${\displaystyle m_{xy}=|\mu _{x}-\mu _{y}|}$ обозначает расстояние между средства из Икс и Y.

В случае, когда Икс и Y зависят друг от друга, имея совместная функция плотности вероятности ж(Икс, y) метрика L – K имеет следующий вид:

${\displaystyle \int _{-\infty }^{\infty }\int _{-\infty }^{\infty }|x-y|f(x,y)\,dx\,dy.}$

Пример: две непрерывные случайные величины с нормальным распределением (NN)

Если обе случайные величины Икс и Y имеют нормальные распределения с тем же стандартное отклонение σ, а если к тому же Икс и Y независимы, то D(Икс, Y) дан кем-то

${\displaystyle D_{NN}(X,Y)=\mu _{xy}+{\frac {2\sigma }{\sqrt {\pi }}}\operatorname {exp} \left(-{\frac {\mu _{xy}^{2}}{4\sigma ^{2}}}\right)-\mu _{xy}\operatorname {erfc} \left({\frac {\mu _{xy}}{2\sigma }}\right),}$

куда

${\displaystyle \mu _{xy}=\left|\mu _{x}-\mu _{y}\right|,}$

где erfc (Икс) является дополнительным функция ошибки и где нижние индексы NN указывают тип метрики L – K.

В этом случае минимально возможное значение функции ${\displaystyle D_{NN}(X,Y)}$ дан кем-то

${\displaystyle \lim _{\mu _{xy}\to 0}D_{NN}(X,Y)=D_{NN}(X,X)={\frac {2\sigma }{\sqrt {\pi }}}.}$

Пример: две непрерывные случайные величины с равномерным распределением (RR)

Когда обе случайные величины Икс и Y имеют равномерные распределения (р) того же самого стандартное отклонение σ, D(Икс, Y) дан кем-то

${\displaystyle D_{RR}(X,Y)={\begin{cases}{\frac {24{\sqrt {3}}\sigma ^{3}-\mu _{xy}^{3}+6{\sqrt {3}}\sigma \mu _{xy}^{2}}{36\sigma ^{2}}},&\mu _{xy}<2{\sqrt {3}}\sigma ,\\\mu _{xy},&\mu _{xy}\geq 2{\sqrt {3}}\sigma .\end{cases}}}$

Минимальное значение такой метрики L – K равно

${\displaystyle D_{RR}(X,X)={\frac {2\sigma }{\sqrt {3}}}.}$

Дискретные случайные величины

Если случайные величины Икс и Y характеризуются дискретное распределение вероятностей метрика Лукашика – Кармовского D определяется как:

${\displaystyle D(X,Y)=\sum _{i}\sum _{j}|x_{i}-y_{j}|P(X=x_{i})P(Y=y_{j}).\,}$

Например для двух дискретных Распределенный по Пуассону случайные переменные Икс и Y приведенное выше уравнение преобразуется в:

${\displaystyle D_{PP}(X,Y)=\sum _{x=0}^{n}\sum _{y=0}^{n}|x-y|{\frac {{\lambda _{x}}^{x}{\lambda _{y}}^{y}e^{-(\lambda _{x}+\lambda _{y})}}{x!y!}}.}$

Случайные векторы

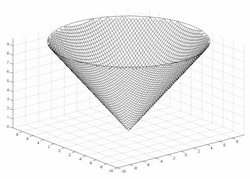
эквидистантная поверхность для евклидовой метрики ${\displaystyle d^{2}(\mathbf {x} ,\mathbf {0} )={\sqrt {x_{1}^{2}+x_{2}^{2}}}}$

эквидистантная поверхность для евклидовой L – K-метрики ${\displaystyle D_{R\delta }^{2}(\mathbf {X} ,\mathbf {0} )\left(\left(\mathbf {X,0} \right):\Omega \to \mathbb {R} ^{2}\right)}$

Метрику случайных величин Лукашика – Кармовского легко расширить до метрики D(Икс, Y) из случайные векторы Икс, Y путем замены ${\displaystyle |x-y|}$ с любым метрическим оператором d(Икс,y):

${\displaystyle D(\mathbf {X} ,\mathbf {Y} )=\int _{\Omega }\int _{\Omega }d(\mathbf {x} ,\mathbf {y} )F(\mathbf {x} )G(\mathbf {y} )\,d\Omega _{x}\,d\Omega _{y}.}$

Например, подставив d(Икс,y) с Евклидова метрика и предполагая двумерность случайных векторов Икс, Y даст:

${\displaystyle D(\mathbf {X} ,\mathbf {Y} )=\int _{\Omega }\int _{\Omega }{\sqrt {\sum _{i=1}^{2}|x_{i}-y_{i}|^{2}}}F(x_{1},x_{2})G(y_{1},y_{2})\,dx_{1}\,dx_{2}\,dy_{1}\,dy_{2}.}$

Эта форма метрики L – K также больше нуля для тех же измеряемых векторов (за исключением двух векторов, имеющих Дельта Дирака коэффициентов) и удовлетворяет условиям неотрицательности и симметрии метрики. Доказательства аналогичны доказательствам для L – K-метрики случайных величин, обсуждавшейся выше.

В случае случайных векторов Икс и Y зависят друг от друга, разделяя общие совместное распределение вероятностей F(Икс, Y) метрика L – K имеет вид:

${\displaystyle D(\mathbf {X} ,\mathbf {Y} )=\int _{\Omega }\int _{\Omega }d(\mathbf {x} ,\mathbf {y} )F(\mathbf {x} ,\mathbf {y} )\,d\Omega _{x}\,d\Omega _{y}.}$

Случайные векторы - евклидова форма

Если случайные векторы Икс и Y не только взаимно независимы, но и все компоненты каждого вектора взаимно независимый, метрика Лукашика – Кармовского для случайных векторов определяется как:

${\displaystyle D_{**}^{(p)}(\mathbf {X} ,\mathbf {Y} )=\left({\sum _{i}{D_{**}(X_{i},Y_{i})}^{p}}\right)^{\frac {1}{p}}}$

куда:

${\displaystyle D_{**}(X_{i},Y_{i})\,}$

- это особая форма L – K-метрики случайных величин, выбранная в зависимости от распределений конкретных коэффициентов ${\displaystyle X_{i}}$ и ${\displaystyle Y_{i}}$ векторов Икс, Y .

Такая форма метрики L – K также имеет общие свойства всех метрик L – K.

• Это не удовлетворяют тождеству неразличимого условия:

${\displaystyle \forall {\mathbf {X} ,\mathbf {Y} }\ D_{**}^{(p)}(\mathbf {X} ,\mathbf {Y} )=0\ \nLeftrightarrow \ \mathbf {X} =\mathbf {Y} \,}$

поскольку:

${\displaystyle D_{**}^{(p)}(\mathbf {X} ,\mathbf {X} )=0\Leftrightarrow \ \forall {i}\ D_{**}(X_{i},X_{i})=0}$

но из свойств метрики L – K для случайных величин следует, что:

${\displaystyle \exists \ X_{i}\ D_{**}(X_{i},X_{i})>0}$

• Он неотрицательный и симметричный, поскольку конкретные коэффициенты также неотрицательны и симметричны:

${\displaystyle \forall \ i\ D_{**}(X_{i},Y_{i})>0\,}$

${\displaystyle \forall \ i\ D_{**}(X_{i},Y_{i})=D_{**}(Y_{i},X_{i})}$

• Он удовлетворяет неравенству треугольника:

${\displaystyle \forall \ \mathbf {X} ,\mathbf {Y} ,\mathbf {Z} \ D_{**}^{(p)}(\mathbf {X} ,\mathbf {Z} )\leq D_{**}^{(p)}(\mathbf {X} ,\mathbf {Y} )+D_{**}^{(p)}(\mathbf {Y} ,\mathbf {Z} )}$

поскольку (ср. Неравенство Минковского ):

${\displaystyle {\begin{aligned}&{}\left({\sum _{i}{D_{**}(X_{i},Y_{i})}^{p}}\right)^{\frac {1}{p}}+\left({\sum _{i}{D_{**}(Y_{i},Z_{i})}^{p}}\right)^{\frac {1}{p}}\ \geq \\&{}\geq \left({\sum _{i}{D_{**}(X_{i},Y_{i})+D_{**}(Y_{i},Z_{i})}^{p}}\right)^{\frac {1}{p}}\geq \\&{}\geq \left({\sum _{i}{D_{**}(X_{i},Z_{i})}^{p}}\right)^{\frac {1}{p}}\end{aligned}}}$

Физическая интерпретация

Метрику Лукашика – Кармовского можно рассматривать как расстояние между квантовая механика частицы, описанные волновые функции ψ, где вероятность dP что данная частица присутствует в данном объеме пространства dV суммы:

${\displaystyle dP=|\psi (x,y,z)|^{2}dV.\,}$

Квантовая частица в коробке

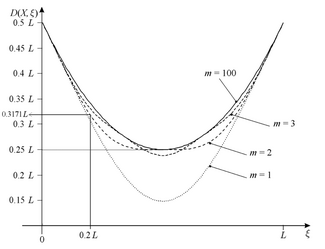
L – K-метрика между квантовой частицей в одномерном ящике длины L и заданная точка ξ коробки ${\displaystyle (0\leq \xi \leq L)}$.

Например, волновая функция кванта частица (Икс) в коробка длины L имеет вид:

${\displaystyle \psi _{m}(x)={\sqrt {\frac {2}{L}}}\sin {\left({\frac {m\pi x}{L}}\right)},\,}$

В этом случае метрика L – K между этой частицей и любой точкой ${\displaystyle \xi \in (0,L)\,}$ Количество коробок:

${\displaystyle {\begin{aligned}&{}D(X,\xi )=\int \limits _{0}^{L}|x-\xi ||\psi _{m}(x)|^{2}dx=\\&{}={\frac {\xi ^{2}}{L}}-\xi +L\left({\frac {1}{2}}-{\frac {\sin ^{2}({\frac {m\pi \xi }{L}})}{m^{2}\pi ^{2}}}\right).\end{aligned}}}$

Из свойств метрики L – K следует, что сумма расстояний между краями ящика (ξ = 0 или ξ= L) и любую заданную точку и метрику L – K между этой точкой и частицей Икс больше, чем метрика L – K между краем ящика и частицей. Например. для квантовой частицы Икс на энергетическом уровне м = 2 и точка ξ = 0.2:

${\displaystyle d(0,0.2L)+D(0.2L,X)\approx 0.2L+0.3171L=0.517L\neq D(0,X)=0.5L=d(0,0.5L).\,}$

Очевидно, метрика L – K между частицей и краем ящика (D (0, X) или D (L, X)) составляет 0,5L и не зависит от уровня энергии частицы.

Две квантовые частицы в коробке

Расстояние между двумя частицы подпрыгивают в одномерном ящике длины L имеющий не зависящий от времени волновые функции:

${\displaystyle \psi _{m}(x)={\sqrt {\frac {2}{L}}}\sin {\left({\frac {m\pi x}{L}}\right)},\,}$

${\displaystyle \psi _{n}(y)={\sqrt {\frac {2}{L}}}\sin {\left({\frac {n\pi y}{L}}\right)},\,}$

можно определить в терминах метрики Лукашика – Кармовского независимый случайные величины как:

${\displaystyle {\begin{aligned}&{}D(X,Y)=\int \limits _{0}^{L}\int \limits _{0}^{L}|x-y||\psi _{m}(x)|^{2}|\psi _{n}(y)|^{2}\,dx\,dy\\&{}={\begin{cases}L\left({\frac {4\pi ^{2}m^{2}-15}{12\pi ^{2}m^{2}}}\right)&m=n,\\L\left({\frac {2\pi ^{2}m^{2}n^{2}-3m^{2}-3n^{2}}{6\pi ^{2}m^{2}n^{2}}}\right)&m\neq n\end{cases}}\end{aligned}}}$

Расстояние между частицами Икс и Y минимален для м = 1 я п = 1, то есть для минимальных уровней энергии этих частиц и составляет:

${\displaystyle \min(D(X,Y))=L\left({\frac {4\pi ^{2}-15}{12\pi ^{2}}}\right)\approx 0.2067L.\,}$

Согласно свойствам этой функции минимальное расстояние отлично от нуля. Для большего уровня энергии м, п он приближается к L/3.

Популярное объяснение

Нормальные распределения двух случайных величин Икс и Y такой же дисперсии для трех мест размещения их средств µ_Икс, µ_y

Предположим, нам нужно измерить расстояние между точками µ_Икс и указать µ_y, которые коллинеарны некоторой точке 0. Предположим далее, что мы поручили эту задачу двум независимым и большим группам геодезистов, оснащенных рулетка, при этом каждый геодезист первой группы будет измерять расстояние между 0 и µ_Икс и каждый геодезист второй группы будет измерять расстояние между 0 и µ_y.

При следующих предположениях мы можем рассматривать два набора полученных наблюдений Икс_я, y_j как случайные величины Икс и Y имея нормальное распределение такой же дисперсии σ ² и распределены по "фактическим местоположениям" точек µ_Икс, µ_y.

Расчет среднее арифметическое для всех пар |Икс_я − y_j| тогда мы должны получить значение метрики L – K D_NN(Икс, Y). Его характерная криволинейность возникает из-за симметрии модуль и перекрытие распределений ж(Икс), грамм(y), когда их средства приближаются друг к другу.

Интересный эксперимент, результаты которого совпадают со свойствами метрики L – K, был проведен в 1967 г. Робертом Мойером и Томас Ландауэр кто измерил точное время, которое потребовалось взрослому, чтобы решить, какая из двух арабских цифр была наибольшей. Когда две цифры были разнесены численно, например, 2 и 9. испытуемые отвечали быстро и точно. Но их время отклика замедлялось более чем на 100 миллисекунд, когда они подходили ближе, например, 5 и 6, и испытуемые затем ошибались так часто, как один раз за каждые десять испытаний. Эффект расстояния присутствовал как среди очень умных людей, так и среди тех, кто был обучен избегать его.^[3]

Практическое применение

Метрику Лукашика – Кармовского можно использовать вместо метрического оператора (обычно Евклидово расстояние ) в различных численных методах и, в частности, в приближенных алгоритмах, таких как сети с радиальными базисными функциями,^[4] обратное взвешивание расстояний или же Кохонен самоорганизующиеся карты.

Этот подход является физически обоснованным, что позволяет учитывать реальную неопределенность местоположения точек отбора проб.^[5][6]

Смотрите также

• Вероятностное метрическое пространство
• Статистическое расстояние

Рекомендации

1. Metryka Pomiarowa, przykłady zastosowań aproksymacyjnych w Mechanice doświadczalnej (Метрика измерений, примеры аппроксимации в экспериментальной механике), Кандидатская диссертация, Шимон Лукашик (автор), Войцех Кармовский (руководитель), Краковский технологический университет имени Тадеуша Костюшко, подан 31 декабря 2001 г., завершен 31 марта 2004 г.
2. Новая концепция вероятностной метрики и ее применения в аппроксимации разрозненных наборов данных, Лукашик Шимон, Вычислительная механика, том 33, номер 4, 299–304, Springer-Verlag 2003 Дои:10.1007 / s00466-003-0532-2
3. Чувство чисел: как разум создает математику, Станислас Дехейн, Oxford University Press, США, 1999 г., ISBN  0-19-513240-8, стр. 73–75
4. Флориан Хогевинд, Питер Биссолли (2010) Оперативные карты среднемесячной температуры для Региона VI ВМО (Европа и Ближний Восток), IDŐJÁRÁS, Ежеквартальный журнал Венгерской метеорологической службы, Vol. 115, № 1-2, январь – июнь 2011 г., стр. 31-49, с. 41 год
5. Ганг Мэн, Джейн Лоу, Мэри Э. Томпсон (2010) «Получение мелкомасштабных показателей, связанных со здоровьем, с использованием пространственной интерполяции вторичных данных», Международный журнал географии здоровья, 9:50 Дои:10.1186 / 1476-072X-9-50
6. Банда Мэн (2010)Социальные и пространственные детерминанты неравенства неблагоприятных исходов родов в социально развитых обществах, Диссертация (доктор философии по планированию), Университет Ватерлоо, Канада,