Волноводный фильтр - Waveguide filter

А волноводный фильтр является электронный фильтр построен с волновод технологии. Волноводы - это полые металлические каналы, внутри которых электромагнитная волна могут быть переданы. Фильтры - это устройства, позволяющие пропускать сигналы на некоторых частотах ( полоса пропускания ), а другие отвергаются ( полоса задерживания ). Фильтры являются основным компонентом электроинженерия конструкции и имеют множество приложений. К ним относятся отбор из сигналы и ограничение шум. Волноводные фильтры наиболее полезны в микроволновая печь диапазон частот, где они удобного размера и имеют низкую потеря. Примеры СВЧ фильтр использование находятся в спутниковая связь, телефонные сети, и телевизионное вещание.
Волноводные фильтры были разработан во время Второй мировой войны для удовлетворения потребностей радар и электронные средства противодействия, но впоследствии вскоре нашел гражданское применение, например, в микроволновые каналы. Большая часть послевоенных разработок была связана с уменьшением объема и веса этих фильтров, сначала за счет использования новых методов анализа, которые привели к устранению ненужных компонентов, а затем за счет таких инноваций, как двухрежимный режим. полости и новые материалы, такие как керамические резонаторы.
Особенность конструкции волноводных фильтров касается Режим передачи. Системы на основе пар проведение провода и аналогичные технологии имеют только один способ передачи. В волноводных системах возможно любое количество режимов. Это может быть как недостатком, поскольку паразитные моды часто вызывают проблемы, так и преимуществом, поскольку двухрежимная конструкция может быть намного меньше, чем эквивалентная одномодовая конструкция волновода. Основными преимуществами волноводных фильтров перед другими технологиями являются их способность выдерживать большую мощность и низкие потери. Основными недостатками являются их объем и стоимость по сравнению с такими технологиями, как микрополоска фильтры.
Существует большое количество различных типов волноводных фильтров. Многие из них состоят из цепочки связанных резонаторов определенного типа, которые можно смоделировать как лестничная сеть из LC-схемы. Один из наиболее распространенных типов состоит из нескольких связанных резонансные полости. Даже внутри этого типа существует множество подтипов, которые в основном различаются с помощью связь. Эти типы муфт включают отверстия,[w] ирисы,[Икс] и посты. Другие типы волноводных фильтров включают: диэлектрический резонатор фильтры, вставные фильтры, тонкие фильтры, фильтры с гофрированным волноводом и шлейфовые фильтры. Ряд компонентов волновода имеют теория фильтров применяется к их конструкции, но их цель - нечто иное, чем фильтрация сигналов. К таким устройствам относятся согласование импеданса составные части, направленные ответвители, и диплексеры. Эти устройства часто принимают форму фильтра, по крайней мере частично.
Объем
Общее значение волновод, когда термин используется безоговорочно, это полый металлический вид (или иногда диэлектрик заполнены), но возможны и другие волноводные технологии.[1] Объем данной статьи ограничен металлическими трубопроводами. В стоечный волновод Структура - это своего рода вариант, но достаточно связанный, чтобы включить его в эту статью: волна в основном окружена проводящим материалом. Можно построить волноводы из диэлектрических стержней,[2] самый известный пример оптические волокна. Эта тема выходит за рамки статьи за исключением того, что иногда используются диэлектрические стержневые резонаторы. внутри полые металлические волноводы. Линия передачи[o] такие технологии, как проводящие провода и микрополоски, можно рассматривать как волноводы,[3] но обычно таковыми не называются и также выходят за рамки данной статьи.
Базовые концепты
Фильтры
В электроника, фильтры используются, чтобы разрешить сигналы определенного диапазона частоты проходить, блокируя других. Они являются основным строительным блоком электронных систем и имеют множество применений. Среди применений волноводных фильтров - создание дуплексеры, диплексеры,[d] и мультиплексоры; избирательность и шум ограничение в приемники; и гармоническое искажение подавление в передатчики.[4]
Волноводы
Волноводы металлические каналы, используемые для ограничения и направления радиосигналов. Обычно их делают из латуни, но также используются алюминий и медь.[5] Чаще всего они прямоугольные, но другие поперечные сечения такие как круглые или эллиптические. Волноводный фильтр - это фильтр, состоящий из волноводных компонентов. Он имеет такой же диапазон применения, что и другие технологии фильтрации в электронике и радиотехнике, но сильно отличается механически и принципом действия.[6]
Технология, используемая для создания фильтров, в значительной степени выбирается из-за ожидаемой частоты работы, хотя существует большое количество перекрытий. Низкочастотные приложения, такие как аудио электроника использовать фильтры, состоящие из дискретных конденсаторы и индукторы. Где-то в очень высокая частота Band, дизайнеры переходят на использование компонентов из отрезков ЛЭП.[п] Такие конструкции называются фильтры с распределенными элементами. Фильтры из дискретных компонентов иногда называют сосредоточенный элемент фильтры, чтобы различать их. На еще более высоких частотах микроволновая печь полос, конструкция переключается на волноводные фильтры или иногда на комбинацию волноводов и линий передачи.[7]
Волноводные фильтры имеют гораздо больше общего с линейными фильтрами, чем фильтры с сосредоточенными элементами; они не содержат дискретных конденсаторов или катушек индуктивности. Однако конструкция волновода часто может быть эквивалентна (или примерно так) конструкции с сосредоточенными элементами. Действительно, проектирование волноводных фильтров часто начинается с конструкции с сосредоточенными элементами, а затем элементы этой конструкции преобразуются в компоненты волновода.[8]
Режимы

Одно из наиболее важных различий в работе волноводных фильтров по сравнению с конструкциями линий передачи касается режима передачи электромагнитная волна несущий сигнал. В линии передачи волна связана с электрическими токами в паре проводников. Проводники ограничивают токи, параллельные линии, и, следовательно, как магнитные, так и электрические компоненты электромагнитное поле перпендикулярны направлению движения волны. Этот поперечная мода обозначается ТЕМ[l] (поперечный электромагнитный). С другой стороны, существует бесконечно много режимов, которые может поддерживать любой полностью полый волновод, но режим ТЕМ не входит в их число. Волноводные режимы обозначаются TE[м] (поперечный электрический) или TM[n] (поперечный магнитный), за которым следует пара суффиксов, определяющих точный режим.[9]
Такое множество мод может вызвать проблемы в волноводных фильтрах при генерации паразитных мод. Проекты обычно основаны на одном режиме и часто включают функции для подавления нежелательных режимов. С другой стороны, преимущество можно получить, выбрав правильный режим для приложения, а иногда даже используя более одного режима одновременно. Там, где используется только одна мода, волновод можно смоделировать как проводящую линию передачи и применить результаты теории линий передачи.[10]
Отрезать
Другой особенностью волноводных фильтров является наличие определенной частоты, т.е. частота среза, ниже которого передача невозможна. Это означает, что теоретически фильтры нижних частот не могут быть выполнены в волноводах. Однако разработчики часто берут конструкцию фильтра нижних частот с сосредоточенными элементами и преобразуют ее в волноводную реализацию. Следовательно, фильтр является фильтром нижних частот по конструкции и может рассматриваться как фильтр нижних частот для всех практических целей, если частота среза ниже любой частоты, представляющей интерес для приложения. Частота отсечки волновода является функцией режима передачи, поэтому на данной частоте волновод может использоваться в одних режимах, но не в других. Точно так же длина волны проводника[час] (λг) и характеристическое сопротивление[b] (Z0) направляющей на заданной частоте также зависят от режима.[11]
Доминирующий режим
Режим с самой низкой частотой среза из всех режимов называется доминирующим режимом. Между отсечкой и следующим по высоте режимом это единственный режим, который можно передавать, поэтому он описывается как доминирующий. Любые генерируемые паразитные моды быстро ослабляются по длине волновода и вскоре исчезают. Практические конструкции фильтров часто предназначены для работы в доминирующем режиме.[12]
В прямоугольном волноводе TE10[q] режим (показанный на рисунке 2) является доминирующим. Существует полоса частот между отсечкой доминирующей моды и следующей наивысшей отсечкой моды, в которой волновод может работать без какой-либо возможности генерации паразитных мод. Следующие самые высокие режимы отсечки - TE20,[р] ровно в два раза больше TE10 режим, а TE01[s] что также вдвое больше TE10 если используемый волновод имеет обычно используемые соотношение сторон из 2: 1. Самый низкий режим отсечки TM - TM11[т] (показано на рисунке 2), который раз больше доминирующей моды в волноводе 2: 1. Таким образом, существует октава в котором доминирующая мода свободна от паразитных мод, хотя работы слишком близко к отсечке обычно избегают из-за фазовых искажений.[13]
В круглом волноводе преобладает мода TE11[u] и показан на рисунке 2. Следующий по высоте режим - TM01.[v] Диапазон, в котором доминирующая мода гарантированно свободна от паразитных мод, меньше, чем в прямоугольном волноводе; отношение самой высокой частоты к самой низкой составляет приблизительно 1,3 в круглом волноводе по сравнению с 2,0 в прямоугольном волноводе.[14]
Evanescent режимы
Evanescent режимы - это режимы ниже частоты среза. Они не могут распространяться по волноводу на любое расстояние, затухая экспоненциально. Однако они важны для функционирования определенных компонентов фильтра, таких как радужная оболочка и штыри, описанные ниже, поскольку энергия накапливается в исчезающих волновых полях.[15]
Преимущества и недостатки
Как и линейные фильтры, волноводные фильтры всегда имеют несколько полосы пропускания, реплики сосредоточенного элемента прототип. В большинстве схем полезна только самая низкая полоса пропускания (или две самые низкие в случае полосовые фильтры ), а остальные считаются нежелательными ложными артефактами. Это внутреннее свойство технологии и не может быть спроектировано отдельно, хотя конструкция может иметь некоторый контроль над положением частот паразитных полос. Следовательно, в любой данной конструкции фильтра существует верхняя частота, за которой фильтр не сможет выполнять свою функцию. По этой причине настоящие НЧ и фильтры верхних частот не может существовать в волноводе. На некоторой высокой частоте будет паразитная полоса пропускания или полоса задерживания, прерывающая намеченную функцию фильтра. Но, как и в случае с частотой среза волновода, фильтр может быть спроектирован так, чтобы край первой полосы паразитных помех был значительно выше любой интересующей частоты.[16]
Диапазон частот, в которых используются волноводные фильтры, во многом определяется необходимым размером волновода. На более низких частотах волновод должен быть непрактично большим, чтобы поддерживать частоту отсечки ниже рабочей частоты. С другой стороны, фильтры, рабочие частоты которых настолько высоки, что длины волн субмиллиметровые, не могут быть изготовлены с обычным механический цех процессы. На таких высоких частотах оптоволоконная технология становится возможной.[17]
Волноводы - среда с низкими потерями. Потери в волноводах в основном происходят от омический диссипация, вызванная токами, наведенными в стенках волновода. Прямоугольный волновод имеет меньшие потери, чем круглый волновод, и обычно является предпочтительным форматом, но TE01 Круговой режим имеет очень низкие потери и находит применение в связи на большие расстояния. Уменьшить потери можно за счет полировки внутренних поверхностей стенок волновода. В некоторых случаях, когда требуется строгая фильтрация, стенки покрываются тонким слоем золота или серебра для улучшения поверхности. проводимость. Примером таких требований являются спутниковые приложения, которые требуют от своих фильтров низких потерь, высокой избирательности и линейной групповой задержки.[18]
Одним из основных преимуществ волноводных фильтров перед технологиями ПЭМ является качество их резонаторы. Качество резонатора характеризуется параметром, называемым Добротность, или просто Q. В Q волноводных резонаторов на тысячи, на порядки больше, чем резонаторов в режиме ПЭМ.[19] В сопротивление проводников, особенно в индукторах с обмоткой, ограничивает Q резонаторов ТЭМ. Это улучшило Q приводит к более качественным фильтрам в волноводах с большей режекцией полосы заграждения. Ограничение Q в волноводах происходит в основном из-за омических потерь в стенках, описанных ранее, но серебряное покрытие внутренних стенок может более чем в два раза Q.[20]
Волноводы обладают хорошей способностью выдерживать нагрузку, что приводит к применению фильтров в радар.[21] Несмотря на эксплуатационные преимущества волноводных фильтров, микрополоска часто является предпочтительной технологией из-за ее низкой стоимости. Это особенно актуально для потребительских товаров и более низких частот СВЧ. Микрополосковые схемы можно изготавливать по дешевым ценам. печатная схема технологии, и при интеграции на той же печатной плате, что и другие блоки схемы, они несут незначительные дополнительные расходы.[22]
История

Идея волновода для электромагнитных волн была впервые предложена Лорд Рэйли в 1897 г. Рэлей предложил коаксиальная линия передачи Можно удалить центральный проводник, и волны все равно будут распространяться по внутренней части оставшегося цилиндрического проводника, несмотря на то, что больше не существует полной электрической цепи проводников. Он описал это в терминах волны, многократно отражающейся от внутренней стенки внешнего проводника зигзагообразным образом по мере продвижения вниз по волноводу. Рэлей также был первым, кто понял, что существует критическая длина волны, длина волны отсечки, пропорциональная диаметру цилиндра, выше которой распространение волны невозможно. Однако интерес к волноводам угас, потому что более низкие частоты больше подходят для радиосвязи на большие расстояния. Результаты Рэлея на время были забыты, и их пришлось заново открыть в 1930-х годах, когда возродился интерес к микроволнам. Волноводы круглой формы были впервые разработаны компанией Джордж Кларк Саутворт и Дж. Ф. Харгривз в 1932 году.[23]
Первый аналоговый фильтр конструкция, выходящая за рамки простого одиночного резонатора, была создана Джордж Эшли Кэмпбелл в 1910 году и положил начало теории фильтров. Фильтр Кэмпбелла представлял собой конструкцию конденсаторов и катушек индуктивности с сосредоточенными элементами, предложенную его работой с загрузочные катушки. Отто Зобель и другие быстро развили это дальше.[24] Разработка фильтров с распределенными элементами началась еще до Второй мировой войны. Большой доклад на эту тему был опубликован Мейсон и Сайкс в 1937 году;[25] патент[26] поданная Мейсоном в 1927 году, может содержать первый опубликованный дизайн фильтра с использованием распределенных элементов.[27]

Работа Мэйсона и Сайкса была сосредоточена на форматах коаксиального кабеля и сбалансированные пары проводов, но другие исследователи позже применили эти принципы и к волноводам. Большое развитие волноводных фильтров было выполнено во время Второй мировой войны, что было обусловлено необходимостью фильтрации радара и электронные средства противодействия. Многое из этого было на Радиационная лаборатория Массачусетского технологического института (Rad Lab), но были задействованы и другие лаборатории в США и Великобритании, такие как Учреждение телекоммуникационных исследований в Соединенном Королевстве. Среди известных ученых и инженеров Rad Lab были Джулиан Швингер, Натан Маркувиц, Эдвард Миллс Перселл, и Ганс Бете. Бете пробыл в Rad Lab недолго, но там же создал свою теорию апертуры. Теория апертуры важна для фильтров с волноводным резонатором, которые были впервые разработаны в Rad Lab. Их работа была опубликована после войны в 1948 году и включает раннее описание двухрежимных резонаторов Фано и Лоусон.[28]
Теоретическая работа после войны включала соизмеримую линейную теорию Пол Ричардс. Соразмерные линии - это сети, в которых все элементы имеют одинаковую длину (или, в некоторых случаях, кратную единице длины), хотя они могут отличаться по другим размерам, чтобы получить разные характеристические сопротивления.[а] Преобразование Ричардса позволяет принять любую конструкцию с сосредоточенными элементами «как есть» и преобразовать ее непосредственно в конструкцию распределенного элемента с помощью очень простого уравнения преобразования. В 1955 г. К. Курода опубликовал трансформации, известные как Личности Куроды. Это сделало работу Ричарда более пригодной для использования в неуравновешенный и форматы волноводов, устраняя проблемные серии связанных элементов, но прошло некоторое время, прежде чем японские работы Куроды стали широко известны в англоязычном мире.[29] Еще одной теоретической разработкой была сетевой фильтр синтеза подход Вильгельм Кауэр в котором он использовал Чебышевское приближение для определения значений элементов. Работа Кауэра была в значительной степени развита во время Второй мировой войны (Кауэр был убит ближе к ее концу), но не мог быть широко опубликован до окончания боевых действий. Хотя работа Кауэра касается сосредоточенных элементов, волноводные фильтры имеют определенное значение; то Фильтр Чебышева, частный случай синтеза Кауэра, широко используется в качестве прототипа фильтра для конструкций волноводов.[30]
Проекты в 1950-х годах начались с прототипа сосредоточенного элемента (методика, используемая до сих пор), который после различных преобразований пришел к желаемому фильтру в форме волновода. В то время этот подход давал дробная пропускная способность не более чем около 1/5. В 1957 году Лео Янг в Стэнфордский исследовательский институт опубликовал метод построения фильтров, которые началось с прототипом распределенного элемента, прототипом ступенчатого импеданса. Этот фильтр был основан на четвертьволновые трансформаторы импеданса различной ширины и был в состоянии производить проекты с полосой пропускания до октава (относительная пропускная способность 2/3). В статье Янга конкретно рассматриваются объемные резонаторы с прямой связью, но эта процедура может быть применена и к другим типам резонаторов с прямым подключением.[31]

Первый опубликованный отчет о кросс-связанный фильтр связано с Джон Р. Пирс в Bell Labs в патенте 1948 г.[32] Фильтр с перекрестной связью - это фильтр, в котором резонаторы, которые не находятся в непосредственной близости, связаны. Дополнительные степени свободы Таким образом, разработчики могут создавать фильтры с улучшенными характеристиками или, альтернативно, с меньшим количеством резонаторов. В одной из версий фильтра Пирса, показанной на рис. 3, используются резонаторы с круглой волноводной полостью для связи между прямоугольными полостными резонаторами. Поначалу этот принцип мало использовался разработчиками волноводных фильтров, но он широко использовался механический фильтр дизайнеров 1960-х, в частности Р. А. Джонсона в Collins Radio Company.[33]
Первоначальное невоенное применение волноводных фильтров было в микроволновые каналы используются телекоммуникационными компаниями для предоставления позвоночник своих сетей. Эти ссылки также использовались другими отраслями промышленности с большими фиксированными сетями, особенно телевизионными вещательными компаниями. Такие приложения были частью крупных программ капитальных вложений. Теперь они также используются в спутниковая связь системы.[34]
Необходимость частотно-независимой задержки в спутниковых приложениях привела к дополнительным исследованиям волноводных воплощений фильтров с перекрестной связью. Ранее в системах спутниковой связи использовался отдельный компонент для выравнивание задержки. Дополнительные степени свободы, полученные от фильтров с перекрестной связью, позволили создать в фильтре плоскую задержку без ущерба для других рабочих параметров. Компонент, который одновременно функционировал как фильтр и эквалайзер, сэкономил бы ценный вес и место. Потребности в спутниковой связи также побудили исследовать более экзотические режимы резонатора в 1970-х годах. Особую известность в этом отношении занимает работа Э. Л. Гриффина и Ф. А. Янга, которые исследовали лучшие способы для 12-14 ГГц диапазон, когда он начал использоваться для спутников в середине 1970-х годов.[35]
Еще одним компактным нововведением стал диэлектрический резонатор, который может использоваться в других форматах фильтров, а также в волноводе. Впервые они были использованы в фильтре С. Б. Коном в 1965 г. оксид титана как диэлектрический материал. Однако диэлектрические резонаторы, используемые в 1960-х годах, имели очень низкие температурные коэффициенты, обычно в 500 раз хуже, чем механический резонатор, сделанный из инвар, что привело к нестабильности параметров фильтра. Диэлектрические материалы того времени с лучшими температурными коэффициентами имели слишком низкую диэлектрическая постоянная быть полезным для экономии места. Ситуация изменилась с появлением керамических резонаторов с очень низкими температурными коэффициентами в 1970-х годах. Первое из них было от Массе и Пуселя, использовавших тетратитанат бария[примечание 1] в Raytheon в 1972 г. О дальнейших улучшениях сообщили в 1979 г. Bell Labs и Мурата Производство. Bell Labs ' нонатитанат бария[заметка 2] резонатор имел диэлектрическую проницаемость 40 и Q 5000–10 000 при 2-7 ГГц. Современные термостойкие материалы имеют диэлектрическую проницаемость около 90 на микроволновых частотах, но исследования продолжают искать материалы как с низкими потерями, так и с высокой диэлектрической проницаемостью; материалы с более низкой диэлектрической проницаемостью, такие как станнат титанат циркония[заметка 3] (ZST) с диэлектрической проницаемостью 38, все еще иногда используются из-за их свойств с низкими потерями.[36]
Альтернативный подход к созданию меньших волноводных фильтров был обеспечен за счет использования нераспространяющихся затухающих мод. Джейнс и Эдсон предложили волноводные фильтры с затухающей модой в конце 1950-х годов. Методы создания этих фильтров были созданы Крэйвеном и Янгом в 1966 году. С тех пор волноводные фильтры с нераспространяющейся модой стали успешно применяться там, где важны размер или вес волновода.[37]
Относительно недавней технологией, используемой в фильтрах с полыми металлическими волноводами, является Finline, своего рода планарный диэлектрический волновод. Финлайн был впервые описан Полом Мейером в 1972 году.[38]
История мультиплексора

Мультиплексоры были впервые описаны Фано и Лоусоном в 1948 году. Пирс был первым, кто описал мультиплексоры с непрерывными полосами пропускания. Мультиплексирование с использованием направленных фильтров было изобретено Сеймуром Коном и Фрэнком Коулом в 1950-х годах. Мультиплексоры с компенсационным иммитанс Резонаторы на каждом стыке - это в основном работы Э. Г. Кристал и Г. Л. Маттеи в 1960-х годах. Этот метод все еще иногда используется, но современная доступность вычислительной мощности привела к более распространенному использованию методов синтеза, которые могут напрямую создавать согласующие фильтры без необходимости в этих дополнительных резонаторах. В 1965 году Р. Дж. Венцель обнаружил, что фильтры с одинарной оконечной нагрузкой,[k] вместо обычных двухконцевых, они были дополнительными - именно то, что было необходимо для диплексера.[c] Венцель был вдохновлен лекциями теоретика схем Эрнст Гийемен.[39]
Многоканальные, многооктавные мультиплексоры были исследованы Гарольдом Шумахером из Microphase Corporation, и его результаты были опубликованы в 1976 году. Принцип, согласно которому фильтры мультиплексора могут быть согласованы при соединении вместе, путем модификации первых нескольких элементов, таким образом устраняя компенсирующие резонаторы. , был случайно обнаружен EJ Curly около 1968 г., когда он неправильно настроил диплексер. Формальная теория для этого была предложена Дж. Д. Родсом в 1976 г. и обобщена на мультиплексоры Родсом и Ральфом Леви в 1979 г.[40]
С 1980-х годов планарные технологии, особенно микрополосковые, имели тенденцию заменять другие технологии, используемые для создания фильтров и мультиплексоров, особенно в продуктах, предназначенных для потребительского рынка. Недавняя инновация в виде пристенного волновода позволяет реализовать конструкции волноводов на плоской подложке с помощью недорогих технологий производства, аналогичных тем, которые используются для микрополосковых конструкций.[41]
Составные части

Конструкции волноводных фильтров часто состоят из двух разных компонентов, повторяющихся несколько раз. Обычно один компонент представляет собой резонатор или разрыв с сосредоточенным контуром, эквивалентным катушке индуктивности, конденсатора или LC-резонансного контура. Часто тип фильтра берет свое название от стиля этого компонента. Эти компоненты разделены вторым компонентом, отрезком направляющей, который действует как трансформатор импеданса. Трансформаторы импеданса создают впечатление, что альтернативные экземпляры первого компонента имеют различный импеданс. Конечным результатом является эквивалентная схема с сосредоточенными элементами лестничной сети. Фильтры с сосредоточенными элементами обычно лестничная топология, и такая схема является типичной отправной точкой для проектирования волноводных фильтров. На рисунке 4 показана такая лестница. Обычно компоненты волновода являются резонаторами, и эквивалентная схема будет LC-резонаторы вместо показанных конденсаторов и катушек индуктивности, но схемы, подобные рисунку 4, по-прежнему используются в качестве прототипы фильтров с использованием полосового или полосового преобразования.[42]
Параметры производительности фильтра, такие как подавление полосы задерживания и скорость перехода между полосой пропускания и полосой задерживания, улучшаются за счет добавления дополнительных компонентов и, таким образом, увеличения длины фильтра. Если компоненты повторяются идентично, фильтр представляет собой фильтр параметров изображения дизайн, а производительность повышается просто за счет добавления большего количества идентичных элементов. Этот подход обычно используется в конструкциях фильтров, в которых используется большое количество близко расположенных элементов, таких как вафельный фильтр. Для схем, в которых элементы более широко разнесены, лучшие результаты могут быть получены с использованием схемы фильтра синтеза сети, такой как общий фильтр Чебышева и Фильтры Баттерворта. При таком подходе не все элементы схемы имеют одинаковую стоимость, и, следовательно, не все компоненты имеют одинаковые размеры. Кроме того, если дизайн улучшается за счет добавления дополнительных компонентов, тогда все значения элементов должны быть рассчитаны заново с нуля. Как правило, у двух экземпляров проекта не будет общих значений. Волноводные фильтры Чебышева используются там, где требования к фильтрации жесткие, например, в спутниковых приложениях.[43][44]
Трансформатор импеданса
Трансформатор импеданса - это устройство, которое создает импеданс на своем выходе. порт отображаются как другое сопротивление на входном порте. В волноводе это устройство представляет собой просто короткий волновод. Особенно полезен четвертьволновой трансформатор импеданса длина которого равна λг/ 4. Это устройство может превратить емкости в индуктивности и наоборот.[45] Он также имеет полезное свойство превращать элементы, соединенные параллельно, в элементы, соединенные последовательно, и наоборот. В противном случае последовательно соединенные элементы сложно реализовать в волноводе.[46]
Размышления и разрывы
Многие компоненты волноводных фильтров работают за счет внезапного изменения, прерывания пропускающих свойств волновода. Такие неоднородности эквивалентны элементам сосредоточенного импеданса, размещенным в этой точке. Это происходит следующим образом: неоднородность вызывает частичное отражение прошедшей волны обратно по направляющей в противоположном направлении, причем соотношение этих двух величин известно как коэффициент отражения. Это полностью аналогично отражение на линии передачи где существует установленная взаимосвязь между коэффициентом отражения и импедансом, вызвавшим отражение. Этот импеданс должен быть реактивный, то есть это должна быть емкость или индуктивность. Это не может быть сопротивлением, поскольку энергия не была поглощена - она вся либо передается вперед, либо отражается. Примеры компонентов с этой функцией включают радужные оболочки, заглушки и сообщения, все они описаны ниже в этой статье в разделе типов фильтров, в которых они встречаются.[47]
Шаг импеданса
Шаг импеданса - это пример устройства, создающего разрыв. Это достигается скачкообразным изменением физических размеров волновода. Это приводит к скачкообразному изменению характеристического импеданса волновода. Шаг может быть как в E-plane[f] (изменение высоты[j]) или H-плоскость[грамм] (изменение ширины[я]) волновода.[48]
Резонансный резонаторный фильтр
Полостной резонатор
Основным компонентом волноводных фильтров является объемный резонатор. Он состоит из короткого световода, заблокированного с обоих концов. Волны, захваченные внутри резонатора, отражаются назад и вперед между двумя концами. Данная геометрия полости будет резонировать на характерной частоте. Эффект резонанса можно использовать для выборочного пропускания определенных частот. Их использование в структуре фильтра требует, чтобы часть волны могла проходить из одной полости в другую через соединительную структуру. Однако, если отверстие в резонаторе остается небольшим, то правильным подходом к проектированию является проектирование полости так, как если бы она была полностью закрытой, и ошибки будут минимальными. В разных классах фильтров используется ряд различных механизмов связи.[49]
В номенклатуре мод в полости вводится третий индекс, например TE.011. Первые два индекса описывают волну, бегущую вверх и вниз по длине резонатора, то есть они являются номерами поперечных мод, как для мод в волноводе. Третий индекс описывает продольная мода вызвано картина интерференции бегущей и отраженной волн. Третий индекс равен количеству полуволн на длине световода. Наиболее распространенными являются доминирующие режимы: TE101 в прямоугольном волноводе, а TE111 в круглом волноводе. TE011 круговой режим используется там, где очень низкие потери (следовательно, высокие Q) требуется, но не может использоваться в двухрежимном фильтре, поскольку он циркулярно симметричен. Лучшими модами для прямоугольного волновода в двухрежимных фильтрах являются TE103 и TE105. Однако еще лучше TE113 режим круглого волновода, который может достигать Q из 16000 при 12 ГГц.[50]
Винт настройки
Настроечные винты - это винты, вставленные в резонансные полости, которые можно регулировать снаружи волновода. Они обеспечивают тонкую настройку резонансная частота вставляя больше или меньше нити в волновод. Примеры можно увидеть в постфильтре на рисунке 1: каждая полость имеет настроечный винт, закрепленный с помощью джемы и резьбовой герметик. Для винтов, вставленных только на небольшое расстояние, эквивалентная схема представляет собой шунтирующий конденсатор, значение которого увеличивается по мере того, как винт вставляется. Однако, когда винт вставлен на расстояние λ / 4, он резонирует, что эквивалентно последовательному LC-контуру. При его добавлении импеданс меняется с емкостного на индуктивный, то есть знак арифметики меняется.[51]
Ирис

Радужная оболочка - это тонкая металлическая пластина поперек волновода с одним или несколькими отверстиями. Он используется для соединения двух отрезков волновода и является средством создания разрыва. Некоторые из возможных геометрических форм диафрагмы показаны на рисунке 5. Диафрагма, уменьшающая ширину прямоугольного волновода, имеет эквивалентную схему шунтирующей индуктивности, тогда как диафрагма, ограничивающая высоту, эквивалентна шунтирующей емкости. Ирис, ограничивающий оба направления, эквивалентен параллельному LC резонансный контур. Последовательный LC-контур может быть сформирован путем отнесения проводящей части радужной оболочки к стенкам волновода. В узкополосных фильтрах часто используются диафрагмы с небольшими отверстиями. These are always inductive regardless of the shape of the hole or its position on the iris. Circular holes are simple to machine, but elongated holes, or holes in the shape of a cross, are advantageous in allowing the selection of a particular mode of coupling.[52]
Irises are a form of discontinuity and work by exciting evanescent higher modes. Vertical edges are parallel to the electric field (E field) and excite TE modes. The stored energy in TE modes is predominately in the magnetic field (H field), and consequently the lumped equivalent of this structure is an inductor. Horizontal edges are parallel to the H field and excite TM modes. In this case the stored energy is predominately in the E field and the lumped equivalent is a capacitor.[53]
It is fairly simple to make irises that are mechanically adjustable. A thin plate of metal can be pushed in and out of a narrow slot in the side of the waveguide. The iris construction is sometimes chosen for this ability to make a variable component.[54]
Iris-coupled filter

An iris-coupled filter consists of a cascade of impedance transformers in the form of waveguide resonant cavities coupled together by irises.[43] In high power applications capacitive irises are avoided. The reduction in height of the waveguide (the direction of the E field) causes the electric field strength across the gap to increase and arcing (or dielectric breakdown if the waveguide is filled with an insulator) will occur at a lower power than it would otherwise.[55]
Post filter
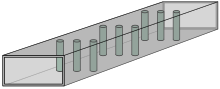
Posts are conducting bars, usually circular, fixed internally across the height of the waveguide and are another means of introducing a discontinuity. A thin post has an equivalent circuit of a shunt inductor. A row of posts can be viewed as a form of inductive iris.[56]
A post filter consists of several rows of posts across the width of the waveguide which separate the waveguide into resonant cavities as shown in figure 7. Differing numbers of posts can be used in each row to achieve varying values of inductance. An example can be seen in figure 1. The filter operates in the same way as the iris-coupled filter but differs in the method of construction.[57]
Post-wall waveguide
A post-wall waveguide, or substrate integrated waveguide, is a more recent format that seeks to combine the advantages of low radiation loss, high Q, and high power handling of traditional hollow metal pipe waveguide with the small size and ease of manufacture of planar technologies (such as the widely used microstrip format). It consists of an insulated substrate pierced with two rows of conducting posts which stand in for the side walls of the waveguide. The top and bottom of the substrate are covered with conducting sheets making this a similar construction to the triplate формат. The existing manufacturing techniques of печатная плата или low temperature co-fired ceramic can be used to make post-wall waveguide circuits. This format naturally lends itself to waveguide post filter designs.[58]
Dual-mode filter
A dual-mode filter is a kind of resonant cavity filter, but in this case each cavity is used to provide two resonators by employing two modes (two polarizations), so halving the volume of the filter for a given order. This improvement in size of the filter is a major advantage in aircraft авионика and space applications. High quality filters in these applications can require many cavities which occupy significant space.[59]
Dielectric resonator filter

Dielectric resonators are pieces of диэлектрик material inserted into the waveguide. They are usually cylindrical since these can be made without механическая обработка but other shapes have been used. They can be made with a hole through the centre which is used to secure them to the waveguide. There is no field at the centre when the TE011 circular mode is used so the hole has no adverse effect. The resonators can be mounted coaxial to the waveguide, but usually they are mounted transversally across the width as shown in figure 8. The latter arrangement allows the resonators to be tuned by inserting a screw through the wall of the waveguide into the centre hole of the resonator.[60]
When dielectric resonators are made from a high permittivity material, such as one of the barium titanates, they have an important space saving advantage compared to cavity resonators. However, they are much more prone to spurious modes. In high-power applications, metal layers may be built into the resonators to conduct heat away since dielectric materials tend to have low теплопроводность.[61]
The resonators can be coupled together with irises or impedance transformers. Alternatively, they can be placed in a stub-like side-housing and coupled through a small aperture.[62]
Insert filter

В insert filters one or more metal sheets are placed longitudinally down the length of the waveguide as shown in figure 9. These sheets have holes punched in them to form resonators. The air dielectric gives these resonators a high Q. Several parallel inserts may be used in the same length of waveguide. More compact resonators may be achieved with a thin sheet of dielectric material and printed metallisation instead of holes in metal sheets at the cost of a lower resonator Q.[63]
Finline filter
Finline is a different kind of waveguide technology in which waves in a thin strip of dielectric are constrained by two strips of metallisation. There are a number of possible topological arrangements of the dielectric and metal strips. Finline is a variation of slot-waveguide but in the case of finline the whole structure is enclosed in a metal shield. This has the advantage that, like hollow metal waveguide, no power is lost by radiation. Finline filters can be made by printing a metallisation pattern on to a sheet of dielectric material and then inserting the sheet into the E-plane of a hollow metal waveguide much as is done with insert filters. The metal waveguide forms the shield for the finline waveguide. Resonators are formed by metallising a pattern on to the dielectric sheet. More complex patterns than the simple insert filter of figure 9 are easily achieved because the designer does not have to consider the effect on mechanical support of removing metal. This complexity does not add to the manufacturing costs since the number of processes needed does not change when more elements are added to the design. Finline designs are less sensitive to manufacturing tolerances than insert filters and have wide bandwidths.[64]
Evanescent-mode filter
It is possible to design filters that operate internally entirely in evanescent modes. This has space saving advantages because the filter waveguide, which often forms the housing of the filter, does not need to be large enough to support propagation of the dominant mode. Typically, an evanescent mode filter consists of a length of waveguide smaller than the waveguide feeding the input and output ports. In some designs this may be folded to achieve a more compact filter. Tuning screws are inserted at specific intervals along the waveguide producing equivalent lumped capacitances at those points. In more recent designs the screws are replaced with dielectric inserts. These capacitors resonate with the preceding length of evanescent mode waveguide which has the equivalent circuit of an inductor, thus producing a filtering action. Energy from many different evanescent modes is stored in the field around each of these capacitive discontinuities. However, the design is such that only the dominant mode reaches the output port; the other modes decay much more rapidly between the capacitors.[65]
Corrugated-waveguide filter


Corrugated-waveguide filters, также называемый ridged-waveguide filters, consist of a number of ridges, or teeth, that periodically reduce the internal height of the waveguide as shown in figures 10 and 11. They are used in applications which simultaneously require a wide passband, good passband matching, and a wide stopband. They are essentially low-pass designs (above the usual limitation of the cutoff frequency), unlike most other forms which are usually band-pass. The distance between teeth is much smaller than the typical λ/4 distance between elements of other filter designs. Typically, they are designed by the image parameter method with all ridges identical, but other classes of filter such as Chebyshev can be achieved in exchange for complexity of manufacture. In the image design method the equivalent circuit of the ridges is modelled as a cascade of LC half sections. The filter operates in the dominant TE10 mode, but spurious modes can be a problem when they are present. In particular, there is little stopband attenuation of TE20 and TE30 modes.[66]
Waffle-iron filter
The waffle-iron filter is a variant of the corrugated-waveguide filter. It has similar properties to that filter with the additional advantage that spurious TE20 and TE30 modes are suppressed. In the waffle-iron filter, channels are cut through the ridges longitudinally down the filter. This leaves a matrix of teeth protruding internally from the top and bottom surfaces of the waveguide. This pattern of teeth resembles a waffle iron, hence the name of the filter.[67]
Waveguide stub filter

А заглушка is a short length of waveguide connected to some point in the filter at one end and short-circuited at the other end. Open-circuited stubs are also theoretically possible, but an implementation in waveguide is not practical because electromagnetic energy would be emitted from the open end of the stub, resulting in high losses. Stubs are a kind of resonator, and the lumped element equivalent is an LC resonant circuit. However, over a narrow band, stubs can be viewed as an impedance transformer. The short-circuit is transformed into either an inductance or a capacitance depending on the stub length.[68]
A waveguide stub filter is made by placing one or more stubs along the length of a waveguide, usually λг/4 apart, as shown in figure 12. The ends of the stubs are blanked off to short-circuit them.[69] When the short-circuited stubs are λг/4 long the filter will be a band-stop filter and the stubs will have a lumped-element approximate equivalent circuit of parallel resonant circuits connected in series with the line. When the stubs are λг/2 long, the filter will be a band-pass filter. In this case the lumped-element equivalent is series LC resonant circuits in series with the line.[70]
Absorption filter
Absorption filters dissipate the energy in unwanted frequencies internally as heat. This is in contrast to a conventional filter design where the unwanted frequencies are reflected back from the input port of the filter. Such filters are used where it is undesirable for power to be sent back towards the source. This is the case with high power transmitters where returning power can be high enough to damage the transmitter. An absorption filter may be used to remove transmitter побочные излучения такие как harmonics or spurious sidebands. A design that has been in use for some time has slots cut in the walls of the feed waveguide at regular intervals. This design is known as a leaky-wave filter. Each slot is connected to a smaller gauge waveguide which is too small to support propagation of frequencies in the wanted band. Thus those frequencies are unaffected by the filter. Higher frequencies in the unwanted band, however, readily propagate along the side guides which are terminated with a matched load where the power is absorbed. These loads are usually a wedge shaped piece of microwave absorbent material.[71] Another, more compact, design of absorption filter uses resonators with a lossy dielectric.[72]
Filter-like devices
There are many applications of filters whose design objectives are something other than rejection or passing of certain frequencies. Frequently, a simple device that is intended to work over only a narrow band or just one spot frequency will not look much like a filter design. Однако широкополосный design for the same item requires many more elements and the design takes on the nature of a filter. Amongst the more common applications of this kind in waveguide are согласование импеданса networks, directional couplers, power dividers, power combiners, и diplexers. Other possible applications include multiplexers, demultiplexers, negative-resistance amplifiers, и time-delay networks.[73]
Согласование импеданса

A simple method of impedance matching is stub matching with a single stub. However, a single stub will only produce a perfect match at one particular frequency. This technique is therefore only suitable for narrow band applications. To widen the bandwidth multiple stubs may be used, and the structure then takes on the form of a stub filter. The design proceeds as if it were a filter except that a different parameter is optimised. In a frequency filter typically the parameter optimised is stopband rejection, passband attenuation, steepness of transition, or some compromise between these. In a matching network the parameter optimised is the impedance match. The function of the device does not require a restriction of bandwidth, but the designer is nevertheless forced to choose a bandwidth because of the структура of the device.[74]
Stubs are not the only format of filter than can be used. In principle, any filter structure could be applied to impedance matching, but some will result in more practical designs than others. A frequent format used for impedance matching in waveguide is the stepped impedance filter. An example can be seen in the duplexer[e] pictured in figure 13.[75]
Directional couplers and power combiners

Directional couplers, power splitters, and power combiners are all essentially the same type of device, at least when implemented with пассивный составные части. A directional coupler splits a small amount of power from the main line to a third port. A more strongly coupled, but otherwise identical, device may be called a power splitter. One that couples exactly half the power to the third port (a 3 dB coupler) is the maximum coupling achievable without reversing the functions of the ports. Many designs of power splitter can be used in reverse, whereupon they become power combiners.[76]
A simple form of directional coupler is two parallel transmission lines coupled together over a λ/4 length. This design is limited because the electrical length of the coupler will only be λ/4 at one specific frequency. Coupling will be a maximum at this frequency and fall away on either side. Similar to the impedance matching case, this can be improved by using multiple elements, resulting in a filter-like structure.[77] A waveguide analogue of this coupled lines approach is the Bethe-hole directional coupler in which two parallel waveguides are stacked on top of each other and a hole provided for coupling. To produce a wideband design, multiple holes are used along the guides as shown in figure 14 and a filter design applied.[78] It is not only the coupled-line design that suffers from being narrow band, all simple designs of waveguide coupler depend on frequency in some way. For instance the rat-race coupler (which can be implemented directly in waveguide) works on a completely different principle but still relies on certain lengths being exact in terms of λ.[79]
Diplexers and duplexers
A diplexer is a device used to combine two signals occupying different frequency bands into a single signal. This is usually to enable two signals to be transmitted simultaneously on the same communications channel, or to allow transmitting on one frequency while receiving on another. (This specific use of a diplexer is called a duplexer.) The same device can be used to separate the signals again at the far end of the channel. The need for filtering to separate the signals while receiving is fairly self-evident but it is also required even when combining two transmitted signals. Without filtering, some of the power from source A will be sent towards source B instead of the combined output. This will have the detrimental effects of losing a portion of the input power and loading source A with the output impedance of source B thus causing mismatch. These problems could be overcome with the use of a 3 dB directional coupler, but as explained in the previous section, a wideband design requires a filter design for directional couplers as well.[80]
Two widely spaced narrowband signals can be diplexed by joining together the outputs of two appropriate band-pass filters. Steps need to be taken to prevent the filters from coupling to each other when they are at resonance which would cause degradation of their performance. This can be achieved by appropriate spacing. For instance, if the filters are of the iris-coupled type then the iris nearest to the filter junction of filter A is placed λГБ/4 from the junction where λГБ is the guide wavelength in the passband of filter B. Likewise, the nearest iris of filter B is placed λga/4 from the junction. This works because when filter A is at resonance, filter B is in its stopband and only loosely coupled and vice versa. An alternative arrangement is to have each filter joined to a main waveguide at separate junctions. A decoupling resonator is placed λг/4 from the junction of each filter. This can be in the form of a short-circuited stub tuned to the resonant frequency of that filter. This arrangement can be extended to multiplexers with any number of bands.[81]
For diplexers dealing with contiguous passbands proper account of the кроссовер characteristics of filters needs to be considered in the design. An especially common case of this is where the diplexer is used to split the entire spectrum into low and high bands. Here a low-pass and a high-pass filter are used instead of band-pass filters. The synthesis techniques used here can equally be applied to narrowband multiplexers and largely remove the need for decoupling resonators.[82]
Directional filters
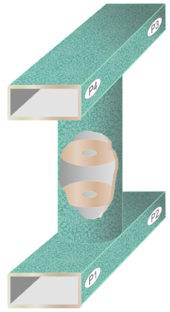
A directional filter is a device that combines the functions of a directional coupler and a diplexer. As it is based on a directional coupler it is essentially a four-port device, but like directional couplers, port 4 is commonly permanently terminated internally. Power entering port 1 exits port 3 after being subject to some filtering function (usually band-pass). The remaining power exits port 2, and since no power is absorbed or reflected this will be the exact complement of the filtering function at port 2, in this case band-stop. In reverse, power entering ports 2 and 3 is combined at port 1, but now the power from the signals rejected by the filter is absorbed in the load at port 4. Figure 15 shows one possible waveguide implementation of a directional filter. Two rectangular waveguides operating in the dominant TE10 mode provide the four ports. These are joined together by a circular waveguide operating in the circular TE11 режим. The circular waveguide contains an iris coupled filter with as many irises as needed to produce the required filter response.[83]
Глоссарий
- ^ отверстие
- An opening in a wall of a waveguide or barrier between sections of waveguide through which electromagnetic radiation can propagate.
- ^ а б характеристическое сопротивление
- Характеристический импеданс, symbol Z0, of a waveguide for a particular mode is defined as the ratio of the transverse electric field to the transverse magnetic field of a wave travelling in one direction down the guide. The characteristic impedance for air filled waveguide is given by,
- ^ c d е diplexer, duplexer
- A diplexer combines or separates two signals occupying different passbands. A duplexer combines or splits two signals travelling in opposite directions, or of differing polarizations (which may also be in different passbands as well).
- ^ E-plane
- The E-plane is the plane lying in the direction of the transverse electric field, that is, vertically along the guide.[85]
- ^ guide wavelength
- Guide wavelength, symbol λг, is the wavelength measured longitudinally down the waveguide. For a given frequency, λг depends on the mode of transmission and is always longer than the wavelength of an electromagnetic wave of the same frequency in free space. λг is related to the cutoff frequency, жc, by,
- ^ H-plane
- The H-plane is the plane lying in the direction of the transverse magnetic field (ЧАС being the analysis symbol for magnetic field strength ), that is, horizontally along the guide.[85]
- ^ я j height, width
- Of a rectangular guide, these refer respectively to the small and large internal dimensions of its cross-section. The polarization of the E-field of the dominant mode is parallel to the height.
- ^ Ирис
- A conducting plate fitted transversally across the waveguide with a, usually large, aperture.
- ^ singly terminated, doubly terminated
- A doubly terminated filter (the normal case) is one where the generator and load, connected to the input and output ports respectively, have impedances matching the filter characteristic impedance. A singly terminated filter has a matching load, but is driven either by a low impedance voltage source or a high impedance current source.[87]
- ^ TEM mode
- Transverse electromagnetic mode, a transmission mode where all the electric field and all the magnetic field are perpendicular to the direction of travel of the electromagnetic wave. This is the usual mode of transmission in pairs of conductors.[88]
- ^ TE mode
- Transverse electric mode, one of a number of modes in which all the electric field, but not all the magnetic field, is perpendicular to the direction of travel of the electromagnetic wave. They are designated H modes in some sources because these modes have a longitudinal magnetic component. The first index indicates the number of half wavelengths of field across the width of the waveguide, and the second index indicates the number of half wavelengths across the height. Properly, the indices should be separated with a comma, but usually they are run together, as mode numbers in double figures rarely need to be considered. Some modes specifically mentioned in this article are listed below. All modes are for rectangular waveguide unless otherwise stated.[89]
- ^ TE01 Режим
- A mode with one half-wave of electric field across the height of the guide and uniform electric field (zero half-waves) across the width of the guide.
- ^ TE10 Режим
- A mode with one half-wave of electric field across the width of the guide and uniform electric field across the height of the guide.
- ^ TE20 Режим
- A mode with two half-waves of electric field across the width of the guide and uniform electric field across the height of the guide.
- ^ TE11 circular mode
- A mode with one full-wave of electric field around the circumference of the guide and one half-wave of electric field along a radius.
- ^ TM mode
- Transverse magnetic mode, one of a number of modes in which all the magnetic field, but not all the electric field, is perpendicular to the direction of travel of the electromagnetic wave. They are designated E modes in some sources because these modes have a longitudinal electric component. See TE mode for a description of the meaning of the indices. Some modes specifically mentioned in this article are:
- ^ TM11 Режим
- A mode with one half-wave of magnetic field across the width of the guide and one half-wave of magnetic field across the height of the guide. This is the lowest TM mode, since TMм0 modes cannot exist.[90]
- ^ TM01 circular mode
- A mode with uniform magnetic field around the circumference of the guide and one half-wave of magnetic field along a radius.
- ^ о п линия передачи
- A transmission line is a signal transmission medium consisting of a pair of electrical conductors separated from each other, or one conductor and a common return path. In some treatments waveguides are considered to be within the class of transmission lines, with which they have much in common. In this article waveguides are not included so that the two types of medium can more easily be distinguished and referred.
Примечания
Рекомендации
- ^ Gibilisco & Sclater, page 913
- ^ Yeh & Shimabukuro, page 1
- ^ Russer, pages 131–132
- ^ Белов и другие., page 147
- ^ Connor, page 52
- ^ Hunter, page 201
- Matthaei и другие., page 243
- ^ Hitchcock & Patterson, page 263
- Bagad, pages 1.3–1.4
- ^ Matthaei и другие., page 83
- ^ Connor, pages 52–53
- Hunter, pages 201, 203
- Matthaei и другие., page 197
- ^ Hunter, pages 255–260
- Matthaei и другие., page 197
- ^ Hunter, pages 201–202
- Matthaei и другие., page 197
- ^ Elmore & Heald, page 289
- Mahmoud, pages 32–33
- ^ Hunter, page 209,
- Matthaei и другие., page 198
- ^ Matthaei и другие., pages 198, 201
- ^ Das & Das, page 112
- ^ Lee, page 789
- Matthaei и другие., page 541
- Sorrentino & Bianchi, page 262
- ^ Hunter, page 201
- Eskelinen & Eskelinen, page 269
- Middleton & Van Valkenburg, pages 30.26–30.28
- ^ Белов и другие., page 147
- Connor, pages 6, 64
- Hunter, page 230
- Matthaei и другие., page 243
- ^ Sorrentino & Bianchi, page 691
- Hunter, page 201
- ^ Hunter, pages 201, 230
- ^ Белов и другие., page 147
- Bowen, page 114
- ^ Das & Das, page 310
- Waterhouse, page 8
- ^ Саркар и другие., pages 90, 129, 545–546
- ^ Bray, page 62
- ^ Levy & Cohn, page 1055
- See also Mason & Sykes (1937)
- ^ Mason, Warren P., "Wave filter", U.S. Patent 1,781,469, filed: 25 июн 1927, issued: 11 ноября 1930.
- ^ Millman и другие., page 108
- ^ Levy & Cohn, pages 1055, 1057
- See also Fano and Lawson (1948)
- ^ Levy and Cohn, pages 1056–1057
- See also Richards (1948)
- ^ Cauer и другие., pages 3, 5
- Mansour, page 166
- ^ Levy & Cohn, page 1056
- See also Young (1963)
- ^ Pierce, J. R., "Guided wave frequency range transducer", U.S. Patent 2,626,990, filed: 4 May 1948, issued: 27 January 1953.
- See also Pierce (1949)
- ^ Levy & Cohn, pages 1060–1061
- ^ Hunter, page 230
- Huurdeman, pages 369–371
- ^ Levy & Cohn, pages 1061–1062
- See also Griffin & Young (1978)
- ^ Levy & Cohn, pages 1062–1063
- Nalwa, pages 525–526
- Смотрите также:
Maasé & Pucel (1972) - Cohn (1965)
- ^ Zhang, Wang, Li, and Lui (2008)
- ^ Srivastava &Gupta, page 82
- See also: Meier (1972)
- ^ Levy & Cohn, page 1065
- Смотрите также:
Fano & Lawson (1948) - Pierce (1949)
- Cristal & Matthaei (1964)
- Wenzel (1969)
- Смотрите также:
- ^ Levy & Cohn, pages 1064–1065
- Смотрите также:
Schumacher (1976) - Rhodes (1976)
- Rhodes & Levy (1979)
- Смотрите также:
- ^ Levy & Cohn, page 1065
- Xuan & Kishk, page 1
- ^ Matthaei и другие., pages 427–440
- ^ а б Hunter, page 230
- ^ Matthaei и другие., pages 83–84
- ^ Matthaei и другие., pages 144–145
- ^ Matthaei и другие., pages 595–596
- ^ Монтгомери и другие., page 162
- ^ Das & Das, pages 134–135
- ^ Hunter, pages 209–210
- Matthaei и другие., page 243
- ^ Connor, pages 100–101
- Levy & Cohn, page 1062
- ^ Монтгомери и другие., pages 168–169
- ^ Bagad, pages 3.41–3.44
- Matthaei и другие., pages 232–242
- Монтгомери и другие., pages 162–179
- ^ Монтгомери и другие., pages 162–179
- ^ Bagad, page 3.41
- ^ Монтгомери и другие., page 167
- ^ Bagad, pages 3.41–3.44
- Hunter, pages 220–222
- Matthaei и другие., pages 453–454
- ^ Hunter, pages 220–228
- Matthaei и другие., page 540
- ^ Xuan & Kishk, pages 1–2
- ^ Hunter, pages 255–260
- ^ Nalwa, page 525
- Jarry & Beneat, page 10
- ^ Nalwa, pages 525–526
- Jarry & Beneat, page 10
- ^ Nalwa, pages 525–526
- Jarry & Beneat, pages 10–12
- ^ Jarry & Beneat, page 12
- ^ Jarry & Beneat, page 12
- Srivastava & Gupta, pages 82–84
- ^ Jarry & Beneat, pages 3–5
- Golio, page 9.9
- ^ Matthaei и другие., pages 380–390
- ^ Matthaei и другие., pages 390–409
- ^ Connor, pages 32–34
- Radmanesh, pages 295–296
- ^ Ke Wu и другие., page 612
- ^ Matthaei и другие., pages 595–596, 726
- ^ Cristal, pages 182–183
- ^ Minakova & Rud, page 1
- ^ Matthaei и другие., pages 1–13
- ^ Connor, pages 32–34
- Matthaei и другие., page 701
- ^ Das & Das, pages 131–136
- Matthaei и другие., Chapter 6 (pages 255–354)
- ^ Lee, page 193, 201
- ^ Matthaei и другие., page 776
- ^ Ishii, pages 205–206, 212,213
- ^ Bagad, page 4.6
- ^ Maloratsky, pages 165–166
- ^ Matthaei и другие., pages 969–973
- ^ Levy & Cohn, page 1065
- Matthaei и другие., pages 991–992
- ^ Matthaei и другие., pages 843–847
- ^ Connor, page 7
- Matthaei и другие., pages 197–198
- Монтгомери и другие., page 162
- ^ а б Meredith, page 127
- ^ Connor, page 56
- ^ Matthaei и другие., page 104
- ^ Connor, page 2
- Silver, pages 203–204
- ^ Connor, pages 52–54
- ^ Connor, page 60
Библиография
- Bagad, V. S., Microwave Engineering, Technical Publications Pune, 2009 ISBN 81-8431-360-8.
- Belov, Leonid A.; Smolskiy, Sergey M.; Kochemasov, Victor N., Handbook of RF, Microwave, and Millimeter-wave Components, Artech House, 2012 ISBN 1-60807-209-6.
- Bowen, Edward George, A Textbook of Radar, Cambridge University Press, 1954 OCLC 216292853.
- Bray, John, Innovation and the Communications Revolution: From the Victorian Pioneers to Broadband Internet, IEE, 2002 ISBN 0-85296-218-5.
- Cauer, E.; Mathis W.; Pauli, R., "Life and Work of Wilhelm Cauer (1900 – 1945)", Proceedings of the Fourteenth International Symposium of Mathematical Theory of Networks and Systems (MTNS2000), Perpignan, June, 2000 OCLC 65290907.
- Connor, F. R., Wave Transmission, Edward Arnold Ltd., 1972 ISBN 0-7131-3278-7.
- Cohn, S. B., "Microwave filters containing high-Q dielectric resonators", G-MTT Symposium Digest, pages 49–50, 5–7 May 1965.
- Cristal, Edward G., "Analytical solution to a waveguide leaky-wave filter structure", IEEE Transactions on Microwave Theory and Techniques, volume 11, issue 3, pages 182–190, 1963.
- Cristal, Edward G.; Matthaei, G. L., "A technique for the design of multiplexers having contiguous channels", IEEE Transactions on Microwave Theory and Techniques, volume 12, issue 1, pages 88–93, 1964.
- Das, Annapurna; Das, Sisir K, Microwave Engineering, Tata McGraw-Hill Education, 2009 ISBN 0-07-066738-1.
- Elmore, William Cronk; Heald, Mark Aiken, Physics of Waves, Courier Dover Publications, 1969 ISBN 0-486-14065-2.
- Eskelinen, Harri; Eskelinen, Pekka, Microwave Component Mechanics, Artech House, 2003 ISBN 1-58053-589-5.
- Fano, R. M.; Lawson, A. W., "Design of microwave filters", chapter 10 of Ragan, G. L. (ed.), Microwave Transmission Circuits, McGraw-Hill, 1948 OCLC 2205252.
- Gibilisco, Stan; Sclater, Neil, Encyclopedia of Electronics, Tab Professional and Reference Books, 1990 ISBN 0-8306-3389-8.
- Golio, Mike, Commercial Wireless Circuits and Components Handbook, CRC Press, 2002 ISBN 1-4200-3996-2.
- Griffin, E. L.; Young, F. A., "A comparison of four overmoded canonical narrow bandpass filters at 12 GHz", Microwave Symposium Digest, 1978 IEEE-MTT-S International, pages 47–49.
- Gusmano, G.; Bianco, A.; Viticoli, M.; Kaciulis, S.; Mattogno, G.; Pandolfi, L., "Study of Zr1-хSnИксTiO4 thin films prepared by a polymeric precursor route", Surface and Interface Analysis, volume 34, issue 1, pages 690–693, August 2002.
- Hitchcock, R. Timothy; Patterson, Robert M., Radio-Frequency and ELF Electromagnetic Energies: A Handbook for Health Professionals, John Wiley & Sons, 1995 ISBN 0-471-28454-8.
- Hunter, I. C., Theory and Design of Microwave Filters, IET, 2001 ISBN 0-85296-777-2.
- Huurdeman, Anton A., The Worldwide History of Telecommunications, Wiley-IEEE, 2003 ISBN 0-471-20505-2.
- Ishii, Thomas Koryu, Handbook of Microwave Technology: Components and devices, Academic Press, 1995 ISBN 0-12-374696-5.
- Jarry, Pierre; Beneat, Jacques, Design and Realizations of Miniaturized Fractal Microwave and RF Filters, John Wiley & Sons, 2009 ISBN 0-470-48781-X.
- Ke, Wu; Lei, Zhu; Vahldieck, Ruediger, "Microwave passive components", in Chen, Wai-Kei (ed.), The Electrical Engineering Handbook, Academic Press, 2004 ISBN 0-08-047748-8.
- Lee, Thomas H., Planar Microwave Engineering, pages 585–618, Cambridge University Press, 2004 ISBN 0-521-83526-7.
- Levy, R.; Cohn, S. B., "A History of microwave filter research, design, and development", IEEE Transactions: Microwave Theory and Techniques, pages 1055–1067, volume 32, issue 9, 1984.
- Mahmoud, S. F., Electromagnetic waveguides: Theory and Applications, IEE, 1991 ISBN 0-86341-232-7.
- Maloratsky, Leo G., Integrated Microwave Front-ends with Avionics Applications, Artech House, 2012 ISBN 1-60807-206-1.
- Mansour, R. R., "Three-dimensional cryogenic filters" in H. Weinstock, H.; Nisenoff, M., Microwave Superconductivity, pages 161–188, Springer, 2001 ISBN 1-4020-0445-1.
- Mason, W. P.; Sykes, R. A. "The use of coaxial and balanced transmission lines in filters and wide band transformers for high radio frequencies", Технический журнал Bell System, pages 275–302, volume 16, 1937.
- Massé, D. J.; Pucel, R. A., "A temperature-stable bandpass filter using dielectric resonators", Труды IEEE, volume 60, issue 6, pages 730–731, June 1972.
- Matthaei, George L.; Young, Leo; Jones, E. M. T., Microwave Filters, Impedance-Matching Networks, and Coupling Structures, McGraw-Hill, 1964 LCCN 64-7937.
- Meier, Paul J., "Two new integrated-circuit media with special advantages at millimeter wavelengths", 1972 IEEE GMTT International Microwave Symposium, pages 221–223, 22–24 May 1972.
- Meredith, Roger, Engineers' Handbook of Industrial Microwave Heating, IET, 1998 ISBN 0-85296-916-3.
- Middleton, Wendy M.; Van Valkenburg, Mac Elwyn, Reference Data for Engineers: Radio, Electronics, Computers and Communications, Newnes, 2002 ISBN 0-7506-7291-9.
- Millman, S. (ed.), A History of Engineering and Science in the Bell System: Communications Sciences (1925–1980), AT&T Bell Laboratories, 1984 ISBN 0-932764-06-1.
- Minakova, L. B.; Rud, L. A., "Natural-frequency approach to the synthesis of narrow-band waveguide absorption filters", 32nd European Microwave Conference, 2002, 23–26 September 2002, Milan.
- Montgomery, Carol Gray; Dicke, Robert Henry; Purcell, Edward M., Principles of Microwave Circuits, IEE, 1948 ISBN 0-86341-100-2.
- Nalwa, Hari Singh (ed), Handbook of Low and High Dielectric Constant Materials and Their Applications, Academic Press, 1999 ISBN 0-08-053353-1.
- Pierce, J. R., "Paralleled-resonator filters", Proceedings of the IRE, volume 37, pages 152–155, February 1949.
- Radmanesh, Matthew M., Advanced RF and Microwave Circuit Design, AuthorHouse, 2009 ISBN 1-4259-7244-6.
- Rhodes, J. D., "Direct design of symmetrical interacting bandpass channel diplexers", IEE Journal on Microwaves, Optics and Acoustics, volume 1, issue 1, pages 34–40, September 1976.
- Rhodes, J. D.; Levy, R., "A generalized multiplexer theory", IEEE Transactions onMicrowave Theory and Techniques, volume 27, issue 2, pages 99–111, February 1979.
- Richards, Paul I., "Resistor-transmission-line circuits", Труды IRE, volume 36, pages 217–220, February 1948.
- Russer, Peter, Electromagnetics, Microwave Circuits and Antenna Design for Communications Engineering, Artech House, 2003 ISBN 1-58053-532-1.
- Sarkar, T. K.; Mailloux, Robert; Oliner, Arthur A.; Salazar-Palma, M.; Sengupta Dipak L., History of Wireless, John Wiley & Sons, 2006 ISBN 0-471-78301-3.
- Schumacher, H. L., "Coax multiplexers: key to EW signal sorting", Microwave Systems News, pages 89–93, August/September 1976 ISSN 0164-3371
- Silver, Samuel, Microwave Antenna Theory and Design, IEE, 1949 ISBN 0-86341-017-0.
- Sorrentino, Roberto; Bianchi, Giovanni, Microwave and RF Engineering, John Wiley & Sons, 2010 ISBN 0-470-66021-X.
- Srivastava, Ganesh Prasad; Gupta, Vijay Laxmi, СВЧ-устройства и схемы, Прентис-Холл Индии, 2006 г. ISBN 81-203-2195-2.
- Уотерхаус, Род, Микрополосковые патч-антенны: руководство для дизайнера, Springer, 2003 г. ISBN 1-4020-7373-9.
- Венцель, Дж. Р., «Применение методов точного синтеза для проектирования многоканальных фильтров», Протоколы IEEE по теории и методам микроволнового излучения, том 13, выпуск 1, страницы 5–15, январь 1965 г.
- Сюань, Ху Ву; Кишк, Ахмед А., Анализ и проектирование интегрированного волновода с подложкой с использованием эффективного гибридного метода 2D, Морган и Клейпул, 2010 г. ISBN 1-59829-902-6.
- Ага, C .; Симабукуро, Ф. И., Сущность диэлектрических волноводов, Springer, 2008 г. ISBN 0-387-49799-4.
- Янг, Л., «Резонаторные фильтры с прямой связью для широкой и узкой полосы пропускания», IEEE Transactions: теория и методы микроволнового излучения, том МТТ-11, страницы 162–178, май 1963 г.
- Янг, Су Ли; Getsinger, W. J .; Воробей, Л. Р., «Технология МПК тетратитаната бария», Протоколы IEEE по теории и методам микроволнового излучения, том 27, выпуск 7, страницы 655–660, июль 1979 г.
- Чжан, Сяньжун; Ван, Цинюань; Ли, Хун; Лю, Ронгджун, «Компактный волноводный фильтр на нестационарном режиме», Международная конференция по технологии микроволнового и миллиметрового диапазона, 2008 г. (ICMMT 2008), том 1, страницы 323–325, IEEE, 2008.



