Уравнение Ван 'т Гоффа - van t Hoff equation

В Уравнение Ван 'т Гоффа связывает изменение в константа равновесия, K_эквхимической реакции на изменение температура, Т, Учитывая стандартное изменение энтальпии, ΔЧАС^⊖, для процесса. Он был предложен голландским химиком Якобус Хенрикус ван 'т Хофф в 1884 г. в своей книге Études de Dynamique Chimique (Исследования по динамической химии).^[1] Это уравнение иногда также называют уравнением Вуканчича – Вуковича.^[2][3][4]

Уравнение Ван 'т Гоффа широко использовалось для изучения изменений в государственные функции в термодинамическая система. В сюжет Ван Т Хоффа, которое выводится из этого уравнения, особенно эффективно при оценке изменения энтальпия, или полная энергия, и энтропия, или количество доступных микросостояния, из химическая реакция.

Уравнение

В стандартных условиях

Под стандартные условия, уравнение Ван 'т Гоффа имеет вид^[5][6]

${\displaystyle {\frac {d}{dT}}\ln K_{\mathrm {eq} }={\frac {\Delta H^{\ominus }}{RT^{2}}}}$

куда пер обозначает натуральный логарифм и р это постоянная идеального газа. Это уравнение точно при любой температуре. На практике уравнение часто интегрируют между двумя температурами в предположении, что энтальпия реакции ΔЧАС постоянно. Поскольку на самом деле ΔЧАС и энтропия реакции ΔS зависят от температуры для большинства процессов,^[7] интегральное уравнение является только приближенным.

Основное использование интегрированного уравнения - оценка нового константа равновесия на новом абсолютная температура предполагая постоянный стандартная энтальпия изменить температурный диапазон.

Чтобы получить интегрированное уравнение, удобно сначала переписать уравнение Вант-Гоффа в виде^[5]

${\displaystyle {\frac {d\ln K_{\mathrm {eq} }}{d{\frac {1}{T}}}}=-{\frac {\Delta H^{\ominus }}{R}}.}$

Определенный интеграл между температурами Т₁ и Т₂ затем

${\displaystyle \ln {\frac {K_{2}}{K_{1}}}={\frac {\Delta H^{\ominus }}{R}}\left({\frac {1}{T_{1}}}-{\frac {1}{T_{2}}}\right).}$

В этом уравнении K₁ - константа равновесия при абсолютной температуре Т₁, и K₂ - константа равновесия при абсолютной температуре Т₂.

Развитие из термодинамики

Объединяя определение Свободная энергия Гиббса:

${\displaystyle \Delta G^{\ominus }=\Delta H^{\ominus }-T\Delta S^{\ominus },}$

куда S это энтропия системы и уравнение изотермы свободной энергии Гиббса:^[8]

${\displaystyle \Delta G^{\ominus }=-RT\ln K_{\mathrm {eq} },}$

мы получаем

${\displaystyle \ln K_{\mathrm {eq} }=-{\frac {\Delta H^{\ominus }}{RT}}+{\frac {\Delta S^{\ominus }}{R}}.}$

Дифференцирование этого выражения по переменной Т дает уравнение Ван 'т Гоффа.

При условии, что ΔЧАС^⊖ и ΔS^⊖ постоянны, предыдущее уравнение дает пер K как линейная функция от 1/Т и поэтому известен как линейная форма уравнения Ван 'т Гоффа. Следовательно, когда диапазон температур достаточно мал, чтобы стандартная энтальпия реакции и энтропия реакции были по существу постоянными, график зависимости натуральный логарифм константы равновесия в зависимости от взаимный температура дает прямую линию. Наклон линии можно умножить на газовая постоянная р получить стандарт энтальпия изменение реакции, и перехват может быть умножен на р получить стандарт энтропия изменять.

изотерма Ван 'т Гоффа

В Свободная энергия Гиббса изменяется в зависимости от температуры и давления термодинамическая система. В Ван Т Хофф изотерма может использоваться для определения свободной энергии Гиббса для реакций с нестандартным состоянием при постоянной температуре:^[9]

${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}=\Delta _{\mathrm {r} }G+RT\ln Q_{\mathrm {r} },}$

куда Δ_рграмм - свободная энергия Гиббса для реакции, а Q_р это коэффициент реакции. Когда реакция на равновесие, Q_р = K_экв. Изотерма Ван 'т Гоффа может помочь оценить смещение равновесной реакции. Когда Δ_рграмм < 0, реакция движется в прямом направлении. Когда Δ_рграмм > 0, реакция движется в обратном направлении. Видеть Химическое равновесие.

сюжет Ван Т Хоффа

Для обратимая реакция, константа равновесия может быть измерена при различных температурах. Эти данные можно отобразить на графике с пер K_экв на уось и 1/Т на Икс ось. Данные должны иметь линейную зависимость, уравнение для которой может быть найдено путем подбора данных с использованием линейной формы уравнения Ван'та Хоффа.

${\displaystyle \ln K_{\mathrm {eq} }=-{\frac {\Delta H^{\ominus }}{RT}}+{\frac {\Delta S^{\ominus }}{R}}.}$

Этот график называется «графиком Ван 'т Хоффа» и широко используется для оценки энтальпия и энтропия из химическая реакция. Из этого сюжета, −ΔЧАС/р это наклон, а ΔS/р - точка пересечения линейной посадки.

Измеряя константа равновесия, K_экв, при различных температурах график Ван 'т Гоффа можно использовать для оценки реакции при изменении температуры.^[10][11] Зная наклон и точку пересечения графика Ван-т-Гоффа, энтальпию и энтропию реакции можно легко получить, используя

${\displaystyle {\begin{aligned}\Delta H&=-R\times {\text{slope}},\\\Delta S&=R\times {\text{intercept}}.\end{aligned}}}$

График Ван 'т-Гоффа можно использовать для быстрого определения энтальпии химической реакции как качественно, так и количественно. Изменение энтальпии может быть положительным или отрицательным, что приводит к двум основным формам графика Ван 'т Гоффа.

Эндотермические реакции

график Ван 'т Гоффа для эндотермической реакции

Для эндотермическая реакция, тепло поглощается, делая изменение чистой энтальпии положительным. Таким образом, согласно определению уклона:

${\displaystyle {\text{slope}}=-{\frac {\Delta H}{R}},}$

для эндотермический реакция ΔЧАС > 0 (и газовая постоянная р > 0), так

${\displaystyle {\text{slope}}=-{\frac {\Delta H}{R}}<0.}$

Таким образом, для эндотермической реакции график Ван 'т Гоффа всегда должен иметь отрицательный наклон.

Экзотермические реакции

График Ван 'т Гоффа для экзотермической реакции

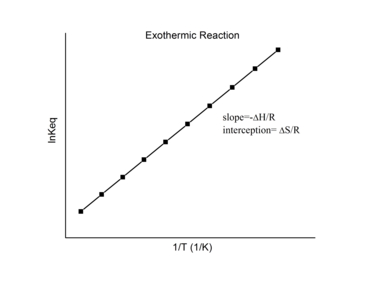
Для экзотермическая реакция, выделяется тепло, в результате чего чистое изменение энтальпии становится отрицательным. Таким образом, согласно определению уклона:

${\displaystyle {\text{slope}}=-{\frac {\Delta H}{R}},}$

из экзотермический реакция ΔЧАС < 0, так

${\displaystyle {\text{slope}}=-{\frac {\Delta H}{R}}>0.}$

Таким образом, для экзотермической реакции график Ван 'т Гоффа всегда должен иметь положительный наклон.

Распространение ошибки

Используя тот факт, что Δграмм^⊖ = −RT пер K = ΔЧАС^⊖ − ТΔS^⊖, казалось бы, что два измерения K достаточно, чтобы получить значение ΔЧАС^⊖:

${\displaystyle \Delta H^{\ominus }=R{\frac {\ln K_{1}-\ln K_{2}}{{\frac {1}{T_{2}}}-{\frac {1}{T_{1}}}}},}$

куда K₁ и K₂ - значения констант равновесия, полученные при температурах Т₁ и Т₂ соответственно. В точность из ΔЧАС^⊖ Значения, полученные таким образом, сильно зависят от точности значений констант равновесия. Типичная пара температур может быть 25 и 35 ° C (298 и 308 K). Для этих температур

${\displaystyle {\frac {1}{T_{2}}}-{\frac {1}{T_{1}}}={\frac {1}{298}}-{\frac {1}{308}}=1.1\times 10^{-4}{\text{ K}}.}$

Вставив это значение в выражение для ΔЧАС^⊖:

${\displaystyle \Delta H^{\ominus }\approx 76\left(\ln K_{1}-\ln K_{2}\right){\text{ kJ/mol}}.}$

Сейчас же, распространение ошибки показывает, что ошибка на ΔЧАС^⊖ будет примерно в 76 кДж / моль раз больше ошибки на (ln K₁ - ln K₂), или примерно в 110 кДж / моль раз больше ошибки пер K значения. Предположим, например, что ошибка на каждом пер K является σ ≈ 0.05, небольшая, но разумная стоимость. Ошибка на ΔЧАС^⊖ будет о 5 кДж / моль. Таким образом, даже несмотря на то, что отдельные константы стабильности были определены с хорошей точностью, энтальпия, вычисленная таким образом, подвержена значительной ошибке.

Тогда энтропия будет получена из ΔS^⊖ = 1/Т(ΔЧАС^⊖ + RT пер K). В этом выражении ошибка второго члена пренебрежимо мала по сравнению с ошибкой первого члена. Тогда коэффициент увеличения равен 76 кДж / моль ÷ 298 К, ​​поэтому при ошибке в логарифмах 0,05 ошибка на ΔS^⊖ будет порядка 17 Дж / (К моль).

Когда константы равновесия измеряются при трех или более температурах, значения ΔЧАС^⊖ будет получен прямолинейный фитинг. В этом случае ошибка стандартной энтальпии будет увеличиваться в несколько меньшей, но все же значительной степени.

Применение сюжета Ван 'т Гоффа

анализ Ван 'т Гоффа

анализ Ван 'т Гоффа

В биологических исследованиях график Ван'т Хоффа также называется анализом Ван'т Гоффа.^[12] Это наиболее эффективно для определения предпочтительного продукта в реакции.

Предположим, что в реакции образуются два продукта B и C:

а А + d D → б B,

а А + d D → c С.

В этом случае, K_экв можно определить как отношение B к C, а не как константу равновесия.

Когда B/C > 1, B - предпочтительный продукт, и данные на графике Ван 'т Гоффа будут в положительной области.

Когда B/C <1, C - предпочтительный продукт, и данные на графике Ван 'т Хоффа будут в отрицательной области.

Используя эту информацию, анализ Ван 'т Гоффа может помочь определить наиболее подходящую температуру для предпочтительного продукта.

В 2010 г. был использован анализ Ван 'т Гоффа, чтобы определить, образует ли вода преимущественно водородная связь с C-терминал или N-терминал из аминокислота пролин.^[13] Константа равновесия для каждой реакции была найдена при различных температурах, и был построен график Ван 'т Гоффа. Этот анализ показал, что энтальпийно вода предпочитает водородную связь с C-конце, но энтропийно он был более благоприятным для водородной связи с N-терминал. В частности, они обнаружили, что C-концевая водородная связь составляла 4,2–6,4 кДж / моль. В N-концевая водородная связь составляла 31–43 Дж / (К · моль).

Сами по себе эти данные не могли сделать вывод, с каким участком вода будет предпочтительно водородной связью, поэтому были использованы дополнительные эксперименты. Было определено, что при более низких температурах энтальпийно предпочтительные частицы вода связывается водородными связями с C-terminus, было предпочтительнее. При более высоких температурах, энтропийно предпочтительные частицы вода связывается водородными связями с N-терминал, было предпочтительнее.

Механистические исследования

Сюжет Ван 'т Гоффа в исследовании механизмов

Химическая реакция может претерпевать разные механизмы реакции при разных температурах.^[14]

В этом случае можно использовать график Ван'т-Хоффа с двумя или более линейными подгонками. Каждая линейная аппроксимация имеет различный наклон и точку пересечения, что указывает на разные изменения энтальпии и энтропии для каждого отдельного механизма. График Ван 'т-Гоффа можно использовать для определения изменения энтальпии и энтропии для каждого механизма и предпочтительного механизма при различных температурах.

${\displaystyle {\begin{aligned}\Delta H_{1}&=-R\times {\text{slope}}_{1},&\Delta S_{1}&=R\times {\text{intercept}}_{1};\\[5pt]\Delta H_{2}&=-R\times {\text{slope}}_{2},&\Delta S_{2}&=R\times {\text{intercept}}_{2}.\end{aligned}}}$

На рисунке в качестве примера реакция протекает по механизму 1 при высокой температуре и по механизму 2 при низкой температуре.

Температурная зависимость

График Ван 'т Гоффа в зависимости от температуры

График Ван 'т Хоффа является линейным на основе молчаливое предположение что энтальпия и энтропия постоянны при изменении температуры. Однако в некоторых случаях энтальпия и энтропия резко меняются с температурой. Приближение первого порядка предполагает, что два разных продукта реакции имеют разную теплоемкость. Включение этого предположения дает дополнительный член c/Т² в выражении для константы равновесия как функции температуры. Затем можно использовать полиномиальную аппроксимацию для анализа данных, которые демонстрируют непостоянную стандартную энтальпию реакции:^[15]

${\displaystyle \ln K_{\mathrm {eq} }=a+{\frac {b}{T}}+{\frac {c}{T^{2}}},}$

куда

${\displaystyle {\begin{aligned}\Delta H&=-R\left(b+{\frac {2c}{T}}\right),\\\Delta S&=R\left(a-{\frac {c}{T^{2}}}\right).\end{aligned}}}$

Таким образом, энтальпию и энтропию реакции можно определить при определенных температурах, даже если существует температурная зависимость.

Самостоятельная сборка ПАВ

Соотношение Ван 'т-Гоффа особенно полезно для определения мицеллообразование энтальпия ΔЧАС^⊖
_м из поверхностно-активные вещества из температурной зависимости критическая концентрация мицелл (CMC):

${\displaystyle {\frac {d}{dT}}\ln \mathrm {CMC} ={\frac {\Delta H_{\mathrm {m} }^{\ominus }}{RT^{2}}}.}$

Однако это соотношение теряет силу, когда номер агрегации также зависит от температуры, и вместо этого следует использовать следующее соотношение:^[16]

${\displaystyle RT^{2}\left({\frac {\partial }{\partial T}}\ln \mathrm {CMC} \right)_{P}=-\Delta H_{\mathrm {m} }^{\ominus }(N)+T\left({\frac {\partial }{\partial N}}\left(G_{N+1}-G_{N}\right)\right)_{T,P}\left({\frac {\partial N}{\partial T}}\right)_{P},}$

с грамм_{N + 1} и грамм_N свободные энергии поверхностно-активного вещества в мицелле с числом агрегации N + 1 и N соответственно. Этот эффект особенно актуален для неионные этоксилированные поверхностно-активные вещества^[17] или же блок-сополимеры полиоксипропилена и полиоксиэтилена (Полоксамеры, Плюроники, Синпероники).^[18] Расширенное уравнение может быть использовано для извлечения числа агрегации самоорганизованных мицелл из дифференциальная сканирующая калориметрия термограммы.^[19]

Смотрите также

• Соотношение Клаузиуса – Клапейрона
• фактор Ван 'т Гоффа (я)
• Уравнение Гиббса – Гельмгольца.
• Равновесие растворимости

Рекомендации

1. Биография на сайте Нобелевской премии. Nobelprize.org (1911-03-01). Проверено 8 ноября 2013.
2. Журнал по моделированию активности TiO2 Prograde и ее значению для Ti в кварцевой термобарометрии пелитовых метаморфических пород. Academia.edu. п. 2.
3. Журнал непрямого спектрофотометрического определения фолиевой кислоты на основе реакции окисления и изучения некоторых термодинамических параметров. Academia.edu. п. 67.
4. Исправление вспомогательной информации PNAS. (PNAS) Труды Национальной академии наук Соединенных Штатов Америки. 30 ноября 2012 г. с. 3.
5. Аткинс, Питер; Де Паула, Хулио (10 марта 2006 г.). Физическая химия (8-е изд.). В. Х. Фриман и компания. п.212. ISBN  978-0-7167-8759-4.
6. Айвз, Д. Дж. Г. (1971). Химическая термодинамика. Университетская химия. Макдональд Технический и научный. ISBN  978-0-356-03736-3.
7. Крейг, Норман (1996). «Диаграммы энтропии». J. Chem. Образовательный. 73 (8): 710. Bibcode:1996JChEd..73..710C. Дои:10.1021 / ed073p710.
8. Дикерсон, Р. Э .; Гейс, И. (1976). Химия, материя и Вселенная. США: W. A. ​​Benjamin Inc. ISBN  978-0-19-855148-5.
9. Монах, Пол (2004). Физическая химия: понимание нашего химического мира. Вайли. п.162. ISBN  978-0471491811.
10. Ким, Тэ Ву (2012). «Динамическое [2] сцепление самоорганизующихся макроциклов Pd (II) в воде». Chem. Латыш. 41: 70. Дои:10.1246 / cl.2012.70.
11. Итикава, Такаюки (2010). «Термодинамические свойства амидов металлов, определяемые изотермами давление-состав аммиака» (PDF). J. Chem. Термодинамика. 42: 140. Дои:10.1016 / j.jct.2009.07.024.
12. "Анализ Вант Хоффа". Группа анализа и дизайна белков.
13. Прелл, Джеймс; Уильямс Э. (2010). "Энтропия вынуждает присоединенную молекулу воды от C- к N-Terminus на протонированном пролине ». Варенье. Chem. Soc. 132 (42): 14733–5. Дои:10.1021 / ja106167d. PMID  20886878.
14. Чатаке, Тошиюки (2010). «Подход к кристаллизации ДНК с помощью термического обратимого процесса дуплексов ДНК». Cryst. Рост Des. 10 (3): 1090. Дои:10.1021 / cg9007075.
15. Дэвид, Виктор (28 апреля 2011 г.). «Отклонение от зависимости Вант-Гоффа в RP-LC, вызванное таутомерным взаимопревращением, наблюдается для четырех соединений». Журнал сепарационной науки. 34 (12): 1423–8. Дои:10.1002 / jssc.201100029. PMID  21538875.
16. Хольцер, Альфред; Хольцер, Мэрилин Ф. (1 мая 2002 г.). «Использование соотношения Вант-Гоффа для определения энтальпии мицеллообразования». Журнал физической химии. 78 (14): 1442–1443. Дои:10.1021 / j100607a026.
17. Херклоц, Хейко; Цамалукас, Алекос; Кита-Токарчик, Катаржина; Струнц, Павел; Гутберлет, Томас (25 ноября 2004 г.). "Структурные, объемные и термодинамические характеристики перехода мицеллярной сферы к стержню". Журнал Американского химического общества. 126 (50): 16544–16552. Дои:10.1021 / ja045525w. PMID  15600359.
18. Табоада, Пабло; Москера, Виктор; Аттвуд, Дэвид; Ян, Чжо; Бут, Колин (5 июня 2003 г.). «Энтальпия мицеллизации диблок-сополи (оксиэтилен / оксипропилен) методом изотермической калориметрии титрования. Сравнение со значением Вант-Гоффа». Физическая химия Химическая физика. 5 (12): 2625–2627. Bibcode:2003PCCP .... 5.2625T. Дои:10.1039 / b303108j.
19. Кьяппизи, Леонардо; Лаззара, Джузеппе; Градзельски, Майкл; Милиото, Стефана (6 декабря 2012 г.). «Количественное описание термограмм индуцированной температуры самоагрегации, определенных методом дифференциальной сканирующей калориметрии» (PDF). Langmuir. 28 (51): 17609–17616. Дои:10.1021 / la303599d. HDL:10447/96872. PMID  23171124.