UPGMA - UPGMA

UPGMA (невзвешенный парно-групповой метод со средним арифметическим) представляет собой простую агломерацию (снизу вверх) иерархическая кластеризация метод. Метод обычно относят к Сокаль и Michener.^[1]

Метод UPGMA аналогичен его взвешенный вариант, WPGMA метод.

Обратите внимание, что невзвешенный член указывает на то, что все расстояния в равной степени влияют на каждое вычисляемое среднее значение, и не относится к математике, с помощью которой оно достигается. Таким образом, простое усреднение в WPGMA дает взвешенный результат, а пропорциональное усреднение в UPGMA дает невзвешенный результат (см. рабочий пример ).^[2]

Алгоритм

Алгоритм UPGMA строит корневое дерево (дендрограмма ), который отражает структуру, присутствующую в попарном матрица сходства (или матрица несходства На каждом шаге ближайшие два кластера объединяются в кластер более высокого уровня. Расстояние между любыми двумя кластерами ${\displaystyle {\mathcal {A}}}$ и ${\displaystyle {\mathcal {B}}}$, каждый размером (т.е., мощность ) ${\displaystyle {|{\mathcal {A}}|}}$ и ${\displaystyle {|{\mathcal {B}}|}}$, принимается среднее значение всех расстояний ${\displaystyle d(x,y)}$ между парами объектов ${\displaystyle x}$ в ${\displaystyle {\mathcal {A}}}$ и ${\displaystyle y}$ в ${\displaystyle {\mathcal {B}}}$, то есть среднее расстояние между элементами каждого кластера:

${\displaystyle {1 \over {|{\mathcal {A}}|\cdot |{\mathcal {B}}|}}\sum _{x\in {\mathcal {A}}}\sum _{y\in {\mathcal {B}}}d(x,y)}$

Другими словами, на каждом шаге кластеризации обновленное расстояние между объединенными кластерами ${\displaystyle {\mathcal {A}}\cup {\mathcal {B}}}$ и новый кластер ${\displaystyle X}$ дается пропорциональным усреднением ${\displaystyle d_{{\mathcal {A}},X}}$ и ${\displaystyle d_{{\mathcal {B}},X}}$ расстояния:

${\displaystyle d_{({\mathcal {A}}\cup {\mathcal {B}}),X}={\frac {|{\mathcal {A}}|\cdot d_{{\mathcal {A}},X}+|{\mathcal {B}}|\cdot d_{{\mathcal {B}},X}}{|{\mathcal {A}}|+|{\mathcal {B}}|}}}$

Алгоритм UPGMA создает корневые дендрограммы и требует предположения о постоянной скорости, то есть предполагает наличие ультраметрический дерево, в котором расстояния от корня до каждого конца ветки равны. Когда подсказки - это молекулярные данные (т.е., ДНК, РНК и белок ), отобранных одновременно, ультраметричность предположение становится эквивалентным предположению молекулярные часы.

Рабочий пример

Этот рабочий пример основан на JC69 матрица генетических расстояний, вычисленная из 5S рибосомальная РНК выравнивание последовательностей пяти бактерий: Bacillus subtilis (${\displaystyle a}$), Bacillus stearothermophilus (${\displaystyle b}$), Лактобациллы viridescens (${\displaystyle c}$), Ахолеплазма хоть (${\displaystyle d}$), и Micrococcus luteus (${\displaystyle e}$).^[3][4]

Первый шаг

• Первая кластеризация

Предположим, что у нас есть пять элементов ${\displaystyle (a,b,c,d,e)}$ и следующая матрица ${\displaystyle D_{1}}$ попарных расстояний между ними:

	а	б	c	d	е
а	0	17	21	31	23
б	17	0	30	34	21
c	21	30	0	28	39
d	31	34	28	0	43
е	23	21	39	43	0

В этом примере ${\displaystyle D_{1}(a,b)=17}$ это наименьшее значение ${\displaystyle D_{1}}$, поэтому мы соединяем элементы ${\displaystyle a}$ и ${\displaystyle b}$.

• Оценка длины первой ветви

Позволять ${\displaystyle u}$ обозначим узел, к которому ${\displaystyle a}$ и ${\displaystyle b}$ теперь подключены. Параметр ${\displaystyle \delta (a,u)=\delta (b,u)=D_{1}(a,b)/2}$ гарантирует, что элементы ${\displaystyle a}$ и ${\displaystyle b}$ равноудалены от ${\displaystyle u}$. Это соответствует ожиданиям ультраметричность гипотеза. ${\displaystyle a}$ и ${\displaystyle b}$ к ${\displaystyle u}$ тогда имейте длину ${\displaystyle \delta (a,u)=\delta (b,u)=17/2=8.5}$ (см. финальную дендрограмму )

• Первое обновление матрицы расстояний

Затем мы приступаем к обновлению исходной матрицы расстояний ${\displaystyle D_{1}}$ в новую матрицу расстояний ${\displaystyle D_{2}}$ (см. ниже), уменьшенного в размере на одну строку и один столбец из-за кластеризации ${\displaystyle a}$ с ${\displaystyle b}$Значения жирным шрифтом в ${\displaystyle D_{2}}$ соответствуют новым расстояниям, рассчитанным по усреднение расстояний между каждым элементом первого кластера ${\displaystyle (a,b)}$ и каждый из оставшихся элементов:

${\displaystyle D_{2}((a,b),c)=(D_{1}(a,c)\times 1+D_{1}(b,c)\times 1)/(1+1)=(21+30)/2=25.5}$

${\displaystyle D_{2}((a,b),d)=(D_{1}(a,d)+D_{1}(b,d))/2=(31+34)/2=32.5}$

${\displaystyle D_{2}((a,b),e)=(D_{1}(a,e)+D_{1}(b,e))/2=(23+21)/2=22}$

Значения, выделенные курсивом в ${\displaystyle D_{2}}$ не затрагиваются обновлением матрицы, поскольку они соответствуют расстояниям между элементами, не участвующими в первом кластере.

Второй шаг

• Вторая кластеризация

Теперь мы повторяем три предыдущих шага, начиная с новой матрицы расстояний. ${\displaystyle D_{2}}$

	(а, б)	c	d	е
(а, б)	0	25.5	32.5	22
c	25.5	0	28	39
d	32.5	28	0	43
е	22	39	43	0

Здесь, ${\displaystyle D_{2}((a,b),e)=22}$ это наименьшее значение ${\displaystyle D_{2}}$, поэтому мы присоединяемся к кластеру ${\displaystyle (a,b)}$ и элемент ${\displaystyle e}$.

• Оценка длины второй ветви

Позволять ${\displaystyle v}$ обозначим узел, к которому ${\displaystyle (a,b)}$ и ${\displaystyle e}$ теперь подключены. Из-за ограничения ультраметричности ветви, соединяющиеся ${\displaystyle a}$ или же ${\displaystyle b}$ к ${\displaystyle v}$, и ${\displaystyle e}$ к ${\displaystyle v}$ равны и имеют следующую длину:${\displaystyle \delta (a,v)=\delta (b,v)=\delta (e,v)=22/2=11}$

Вычисляем недостающую длину ветки:${\displaystyle \delta (u,v)=\delta (e,v)-\delta (a,u)=\delta (e,v)-\delta (b,u)=11-8.5=2.5}$ (увидеть окончательную дендрограмму )

• Обновление матрицы второго расстояния

Затем мы приступаем к обновлению ${\displaystyle D_{2}}$ в новую матрицу расстояний ${\displaystyle D_{3}}$ (см. ниже), уменьшенного в размере на одну строку и один столбец из-за кластеризации ${\displaystyle (a,b)}$ с ${\displaystyle e}$. Значения, выделенные жирным шрифтом ${\displaystyle D_{3}}$ соответствуют новым расстояниям, рассчитанным по пропорциональное усреднение:

${\displaystyle D_{3}(((a,b),e),c)=(D_{2}((a,b),c)\times 2+D_{2}(e,c)\times 1)/(2+1)=(25.5\times 2+39\times 1)/3=30}$

Благодаря этому пропорциональному среднему вычисление этого нового расстояния учитывает больший размер ${\displaystyle (a,b)}$ кластер (два элемента) относительно ${\displaystyle e}$ (один элемент). По аналогии:

${\displaystyle D_{3}(((a,b),e),d)=(D_{2}((a,b),d)\times 2+D_{2}(e,d)\times 1)/(2+1)=(32.5\times 2+43\times 1)/3=36}$

Таким образом, пропорциональное усреднение дает равный вес начальным расстояниям матрицы ${\displaystyle D_{1}}$. Это причина, по которой метод невзвешенныйне по математической процедуре, а по отношению к начальным расстояниям.

Третий шаг

• Третья кластеризация

Мы снова повторяем три предыдущих шага, начиная с обновленной матрицы расстояний. ${\displaystyle D_{3}}$.

	((а, б), д)	c	d
((а, б), д)	0	30	36
c	30	0	28
d	36	28	0

Здесь, ${\displaystyle D_{3}(c,d)=28}$ это наименьшее значение ${\displaystyle D_{3}}$, поэтому мы соединяем элементы ${\displaystyle c}$ и ${\displaystyle d}$.

• Оценка длины третьей ветви

Позволять ${\displaystyle w}$ обозначим узел, к которому ${\displaystyle c}$ и ${\displaystyle d}$ подключены. ${\displaystyle c}$ и ${\displaystyle d}$ к ${\displaystyle w}$ тогда имейте длину ${\displaystyle \delta (c,w)=\delta (d,w)=28/2=14}$ (увидеть окончательную дендрограмму )

• Обновление третьей матрицы расстояний

Необходимо обновить одну запись, имея в виду, что два элемента ${\displaystyle c}$ и ${\displaystyle d}$ каждый имеет вклад ${\displaystyle 1}$ в среднее вычисление:

${\displaystyle D_{4}((c,d),((a,b),e))=(D_{3}(c,((a,b),e))\times 1+D_{3}(d,((a,b),e))\times 1)/(1+1)=(30\times 1+36\times 1)/2=33}$

Заключительный этап

Финал ${\displaystyle D_{4}}$ матрица:

	((а, б), д)	(CD)
((а, б), д)	0	33
(CD)	33	0

Итак, мы присоединяемся к кластерам ${\displaystyle ((a,b),e)}$ и ${\displaystyle (c,d)}$.

Позволять ${\displaystyle r}$ обозначают (корневой) узел, к которому ${\displaystyle ((a,b),e)}$ и ${\displaystyle (c,d)}$ подключены. ${\displaystyle ((a,b),e)}$ и ${\displaystyle (c,d)}$ к ${\displaystyle r}$ тогда имейте длины:

${\displaystyle \delta (((a,b),e),r)=\delta ((c,d),r)=33/2=16.5}$

Вычисляем две оставшиеся длины ветвей:

${\displaystyle \delta (v,r)=\delta (((a,b),e),r)-\delta (e,v)=16.5-11=5.5}$

${\displaystyle \delta (w,r)=\delta ((c,d),r)-\delta (c,w)=16.5-14=2.5}$

Дендрограмма UPGMA

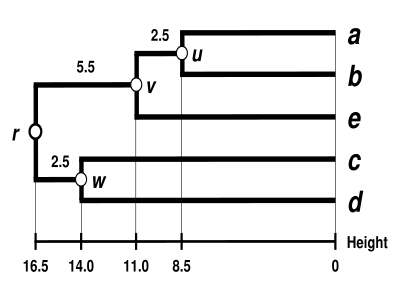
Дендрограмма завершена.^[5] Он ультраметрический, потому что все наконечники (${\displaystyle a}$ к ${\displaystyle e}$) равноудалены от ${\displaystyle r}$ :

${\displaystyle \delta (a,r)=\delta (b,r)=\delta (e,r)=\delta (c,r)=\delta (d,r)=16.5}$

Таким образом, дендрограмма основана на ${\displaystyle r}$, его самый глубокий узел.

Сравнение с другими связями

Альтернативные схемы связи включают однократная кластеризация, полная кластеризация связей, и Кластеризация средних связей WPGMA. Реализация другой связи - это просто вопрос использования другой формулы для расчета межкластерных расстояний на этапах обновления матрицы расстояний в вышеупомянутом алгоритме. Полная кластеризация связей позволяет избежать недостатка альтернативного метода кластеризации одиночных связей - так называемого явление сцепления, где кластеры, сформированные с помощью кластеризации с одной связью, могут быть принудительно объединены из-за того, что отдельные элементы находятся близко друг к другу, даже если многие элементы в каждом кластере могут быть очень удалены друг от друга. Полная связь имеет тенденцию находить компактные группы приблизительно равного диаметра.^[6]

Сравнение дендрограмм, полученных разными методами кластеризации из одного и того же матрица расстояний.

Односвязная кластеризация.	Кластеризация с полной связью.	Кластеризация средней связи: WPGMA.	Средняя кластеризация связей: UPGMA.

Использует

• В экология, это один из самых популярных методов классификации единиц выборки (например, участков растительности) на основе их попарного сходства в соответствующих переменных дескриптора (таких как видовой состав).^[7] Например, его использовали для понимания трофического взаимодействия между морскими бактериями и простейшими.^[8]
• В биоинформатика, UPGMA используется для создания фенетический деревья (фенограммы). UPGMA изначально был разработан для использования в электрофорез белков исследований, но в настоящее время наиболее часто используется для создания направляющих деревьев для более сложных алгоритмов. Этот алгоритм, например, используется в выравнивание последовательностей процедур, поскольку он предлагает один порядок, в котором последовательности будут выровнены. Действительно, направляющее дерево нацелено на группировку наиболее похожих последовательностей, независимо от их скорости эволюции или филогенетического сходства, и это как раз и является целью UPGMA.^[9]
• В филогенетика, UPGMA предполагает постоянную скорость эволюции (гипотеза молекулярных часов ) и что все последовательности были отобраны одновременно, и это не является хорошо зарекомендовавшим себя методом вывода взаимосвязей, если это предположение не было проверено и обосновано для используемого набора данных. Обратите внимание, что даже в условиях «строгой синхронизации» последовательности, выбранные в разное время, не должны приводить к ультраметрическому дереву.

Сложность времени

Тривиальная реализация алгоритма построения дерева UPGMA имеет ${\displaystyle O(n^{3})}$ временная сложность, а использование кучи для каждого кластера для сохранения расстояния от другого кластера сокращает время до ${\displaystyle O(n^{2}\log n)}$. Фионн Муртаг представил некоторые другие подходы для особых случаев, ${\displaystyle O(k3^{k}n^{2})}$ алгоритм времени Дей и Эдельсбруннер^[10] для k-мерных данных, что оптимально ${\displaystyle O(n^{2})}$ для постоянного k, а другой ${\displaystyle O(n^{2})}$ алгоритм для ограниченных входов, когда «агломерационная стратегия удовлетворяет свойству сводимости».^[11]

Смотрите также

• Соседство
• Кластерный анализ
• Односвязная кластеризация
• Кластеризация с полной связью
• Иерархическая кластеризация
• Модели эволюции ДНК
• Молекулярные часы

Рекомендации

1. Сокаль, Michener (1958). «Статистический метод оценки систематических взаимосвязей». Бюллетень науки Канзасского университета. 38: 1409–1438.
2. Гарсия С., Пуигбо П. "DendroUPGMA: Утилита для построения дендрограмм" (PDF). п. 4.
3. Эрдманн В.А., Вольтерс Дж. (1986). «Коллекция опубликованных последовательностей рибосомных РНК 5S, 5.8S и 4.5S». Исследования нуклеиновых кислот. 14 Suppl (Suppl): r1–59. Дои:10.1093 / nar / 14.suppl.r1. ЧВК  341310. PMID  2422630.
4. Olsen GJ (1988). «Филогенетический анализ с использованием рибосомальной РНК». Методы в энзимологии. 164: 793–812. Дои:10.1016 / с0076-6879 (88) 64084-5. PMID  3241556.
5. Swofford DL, Olsen GJ, Waddell PJ, Hillis DM (1996). «Филогенетический вывод». В Hillis DM, Moritz C, Mable BK (ред.). Молекулярная систематика, 2-е издание. Сандерленд, Массачусетс: Синауэр. С. 407–514. ISBN  9780878932825.
6. Everitt, B.S .; Ландау, С .; Лиз, М. (2001). Кластерный анализ. 4-е издание. Лондон: Арнольд. п. 62–64.
7. Лежандр П, Лежандр Л (1998). Числовая экология. Развитие экологического моделирования. 20 (Второе английское изд.). Амстердам: Эльзевир.
8. Васкес-Домингес Э., Касамайор Э.О., Катала П., Лебарон П. (апрель 2005 г.). «Различные морские гетеротрофные нанофлагелляты по-разному влияют на состав обогащенных бактериальных сообществ». Микробная экология. 49 (3): 474–85. Дои:10.1007 / s00248-004-0035-5. JSTOR  25153200. PMID  16003474. S2CID  22300174.
9. Уилер Т.Дж., Кечечиоглу Д.Д. (июль 2007 г.). «Множественное выравнивание путем выравнивания выравниваний». Биоинформатика. 23 (13): i559–68. Дои:10.1093 / биоинформатика / btm226. PMID  17646343.
10. День WH, Эдельсбруннер Х (1984-12-01). «Эффективные алгоритмы методов агломеративной иерархической кластеризации». Журнал классификации. 1 (1): 7–24. Дои:10.1007 / BF01890115. ISSN  0176-4268. S2CID  121201396.
11. Муртаг Ф (1984). «Сложности иерархических алгоритмов кластеризации: современное состояние». Вычислительная статистика ежеквартально. 1: 101–113.

внешняя ссылка

• Реализация алгоритма кластеризации UPGMA на Ruby (AI4R)
• Пример расчета UPGMA с использованием матрицы сходства
• Пример расчета UPGMA с использованием матрицы расстояний