Резонанс - Resonance

Эта статья о резонансе в физике. Для использования в других целях см. Резонанс (значения).

"Resonate" перенаправляется сюда. Для использования в других целях см. Резонировать (значения).

"Резонансный" перенаправляется сюда. Для фонологического термина см. Сонорант.

Увеличение амплитуды по мере уменьшения демпфирования и приближения частоты к резонансной частоте ведомого затухающий простой гармонический осциллятор.^[1][2]

Резонанс описывает явление повышенного амплитуда это происходит, когда частота из периодически применяется сила (или Фурье-компонента его) равна или близка к собственная частота системы, в которой он действует. Когда колеблющийся сила применяется в резонансная частота динамической системы, система будет колебаться с большей амплитудой, чем при приложении той же силы на других, нерезонансных частотах.^[3]

Частоты, при которых амплитуда отклика равна относительный максимум также известны как резонансные частоты или резонансные частоты системы.^[3] Небольшие периодические силы, которые находятся около резонансной частоты системы, могут вызывать колебания большой амплитуды в системе из-за накопления колебательная энергия.

Резонансные явления возникают при всех типах вибрации или волны: есть механический резонанс, акустический резонанс, электромагнитный резонанс, ядерный магнитный резонанс (ЯМР), электронный спиновой резонанс (ESR) и резонанс квантовой волновые функции. Резонансные системы могут использоваться для генерации колебаний определенной частоты (например, музыкальные инструменты ) или выбрать определенные частоты из сложной вибрации, содержащей множество частот (например, фильтры).

Период, термин резонанс (от латинский резонанс, "эхо", от резонанс, 'resound') возникла в области акустики, в частности симпатический резонанс наблюдается в музыкальных инструментах, например, когда одна струна начинает вибрировать и издавать звук после удара по другой. Другой пример, электрический резонанс, встречается в цепь с участием конденсаторы и индукторы потому что коллапсирующее магнитное поле индуктора генерирует электрический ток в его обмотках, который заряжает конденсатор, а затем разряжающийся конденсатор обеспечивает электрический ток, который создает магнитное поле в индукторе. После того, как цепь заряжена, колебания становятся самоподдерживающимися и отсутствуют внешние периодические движущие силы.^{[требуется разъяснение ]} Это аналог механического маятник, где механическая энергия преобразуется туда и обратно между кинетический и потенциал, и обе системы являются формами простые гармонические осцилляторы.

Обзор

Резонанс возникает, когда система способна хранить и легко передавать энергию между двумя или более разными режимы хранения (например, кинетическая энергия и потенциальная энергия в случае простого маятника). Однако от цикла к циклу возникают некоторые потери, называемые демпфирование. При малом затухании резонансная частота примерно равна собственная частота системы, которая представляет собой частоту невынужденных колебаний. Некоторые системы имеют несколько различных резонансных частот.

Примеры

Толкать человека в качели это типичный пример резонанса. Качели нагруженные, маятник, имеет собственная частота колебания, его резонансной частоты, и сопротивляется толканию с большей или меньшей скоростью.

Знакомый пример - детская площадка качели, который действует как маятник. Если подтолкнуть человека к качанию вовремя с естественным интервалом качания (его резонансная частота), качели будут становиться все выше и выше (максимальная амплитуда), а попытки подтолкнуть качели в более быстром или медленном темпе создают меньшие дуги. Это потому, что энергия, поглощаемая качелями, максимальна, когда толчки соответствуют собственным колебаниям качелей.

Резонанс широко встречается в природе и используется во многих искусственных устройствах. Это механизм, с помощью которого практически все синусоидальный генерируются волны и вибрации. Многие звуки, которые мы слышим, например, когда твердые предметы металл, стекло, или дерево ударяются, вызываются кратковременными резонансными колебаниями объекта. Свет и другие короткие волны электромагнитное излучение создается резонансом на атомный масштаб, такие как электроны в атомах. Другие примеры резонанса:

• Хронометражные механизмы современных часов и часов, например, балансир в механическом часы и Кристалл кварца в кварцевые часы
• Приливный резонанс из Залив Фанди
• Акустические резонансы из музыкальные инструменты и человек голосовой тракт
• Разрушение хрустального бокала при воздействии музыкального тона правильного тона (его резонансной частоты)
• Идиофоны трения, например, изготовление стеклянного предмета (стакан, бутылка, ваза) вибрировать потерев ободок кончиком пальца
• Электрический резонанс из настроенные схемы в радио и Телевизоры которые позволяют избирательно принимать радиочастоты
• Создание последовательный свет от оптический резонанс в лазер полость
• Орбитальный резонанс на примере некоторых луны из Солнечная система с газовые гиганты
• Материальные резонансы в атомном масштабе лежат в основе нескольких спектроскопический методы, которые используются в физика конденсированного состояния
  • Электронный спиновой резонанс
  • Эффект Мёссбауэра
  • Ядерный магнитный резонанс

Tacoma Narrows Bridge

Основная статья: Такома узкий мост (1940)

Драматично видимое, ритмичное изгибание, которое привело к краху оригинальной "Galloping Gertie" 1940 года. Tacoma Narrows Bridge, ошибочно охарактеризован как пример явления резонанса в некоторых учебниках.^[3] Катастрофические колебания, разрушившие мост, произошли не из-за простого механического резонанса, а из-за более сложного взаимодействия между мостом и ветром, проходящим через него - явление, известное как аэроупругий флаттер, который является автоколебание или своего рода «самоподдерживающаяся вибрация», как упоминается в нелинейной теории колебаний. Роберт Х. Сканлан, отец мост аэродинамика, написал статью об этом недоразумении.^[4]

Международная космическая станция

В ракетные двигатели для Международная космическая станция (ISS) контролируются автопилот. Обычно загруженные параметры для управления системой управления двигателем модуля «Звезда» заставляют ракетные двигатели выводить Международную космическую станцию ​​на более высокую орбиту. Ракетные двигатели петля - установлен, и обычно экипаж не замечает операции. Однако 14 января 2009 года загруженные параметры заставили автопилот раскачивать ракетные двигатели все большими и большими колебаниями с частотой 0,5 Гц. Эти колебания были записаны на видео и длились 142 секунды.^[5]

Резонанс в линейных системах

Резонанс проявляется во многих линейных и нелинейных системах как колебания вокруг точки равновесия. Когда система приводится в действие синусоидальным внешним входом, измеренный выходной сигнал системы может колебаться в ответ. Отношение амплитуды установившихся колебаний выхода к колебаниям входа называется усилением, и коэффициент усиления может быть функцией частоты синусоидального внешнего входа. Пики усиления на определенных частотах соответствуют резонансам, где амплитуда колебаний измеряемого выхода непропорционально велика.

Поскольку многие линейные и нелинейные системы, которые колеблются, моделируются как гармонические осцилляторы вблизи их положений равновесия этот раздел начинается с определения резонансной частоты для управляемого затухающего гармонического осциллятора. Затем в разделе используется Схема RLC для иллюстрации связи между резонансом и передаточной функцией системы, частотной характеристикой, полюсами и нулями. Основываясь на примере схемы RLC, в разделе затем обобщаются эти отношения для линейных систем более высокого порядка с несколькими входами и выходами.

Резонанс управляемого затухающего гармонического осциллятора

Основная статья: Гармонический осциллятор § Управляемые гармонические осцилляторы

Рассмотрим амортизированную массу на пружине, приводимую в действие синусоидальной внешней силой. Второй закон Ньютона принимает форму

${\displaystyle m{\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}=F_{0}\sin(\omega t)-kx-c{\frac {\mathrm {d} x}{\mathrm {d} t}},}$

(1)

где м это масса, Икс - смещение массы от точки равновесия, F₀ - управляющая амплитуда, ω угловая частота возбуждения, k - жесткость пружины, и c - коэффициент вязкого демпфирования. Это можно переписать в виде

${\displaystyle {\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}+2\zeta \omega _{0}{\frac {\mathrm {d} x}{\mathrm {d} t}}+\omega _{0}^{2}x={\frac {F_{0}}{m}}\sin(\omega t),}$

(2)

где

${\displaystyle \omega _{0}={\sqrt {\frac {k}{m}}}}$ называется незатухающий угловая частота осциллятора или собственная частота,

${\displaystyle \zeta ={\frac {c}{2{\sqrt {mk}}}}}$ называется коэффициент демпфирования.

Многие источники также ссылаются на ω₀ как резонансная частота. Однако, как показано ниже, при анализе колебаний смещения Икс(т) резонансная частота близка, но не такая, как ω₀. Обычно резонансная частота близка к собственной частоте, но не обязательно совпадает с ней.^[6] Пример схемы RLC в следующем разделе дает примеры различных резонансных частот для одной и той же системы.

Общее решение уравнения (2) представляет собой сумму преходящий решение, зависящее от начальных условий и устойчивое состояние решение, которое не зависит от начальных условий и зависит только от движущей амплитуды F₀, частота движения ω, незатухающая угловая частота ω₀, а коэффициент демпфирования ζ. Переходное решение распадается за относительно короткий промежуток времени, поэтому для изучения резонанса достаточно рассмотреть стационарное решение.

Можно написать стационарное решение для Икс(т) как функция, пропорциональная движущей силе с индуцированной фаза изменение φ,

${\displaystyle x(t)={\frac {F_{0}}{m{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}}\sin(\omega t+\varphi ),}$

(3)

где

${\displaystyle \varphi =\arctan \left({\frac {2\omega \omega _{0}\zeta }{\omega ^{2}-\omega _{0}^{2}}}\right)+n\pi .}$

Значение фазы обычно принимается между -180 ° и 0, поэтому оно представляет собой фазовое отставание как для положительных, так и для отрицательных значений аргумента arctan.

Установившееся изменение амплитуды с относительной частотой ${\displaystyle \omega /\omega _{0}}$ и демпфирование ${\displaystyle \zeta }$ ведомого простой гармонический осциллятор

Резонанс возникает, когда на определенных частотах возбуждения установившаяся амплитуда Икс(т) велика по сравнению с его амплитудой на других частотах возбуждения. Для массы на пружине резонанс физически соответствует колебаниям массы, имеющим большие смещения от положения равновесия пружины на определенных частотах движения. Глядя на амплитуду Икс(т) как функция частоты возбуждения ω, амплитуда максимальна на частоте возбуждения

${\displaystyle \omega _{r}=\omega _{0}{\sqrt {1-2\zeta ^{2}}}.}$

ω_р это резонансная частота для этой системы. Снова обратите внимание, что резонансная частота не равна незатухающей угловой частоте. ω₀ осциллятора. Они пропорциональны, и если коэффициент демпфирования стремится к нулю, они одинаковы, но для ненулевого демпфирования они не имеют одинаковой частоты. Как показано на рисунке, резонанс также может возникать на других частотах вблизи резонансной частоты, включая ω₀, но максимальный отклик приходится на резонансную частоту.

Также обратите внимание, что ω_р реально и отличен от нуля, если ${\displaystyle \zeta <1/{\sqrt {2}}}$, поэтому эта система может резонировать только тогда, когда гармонический осциллятор значительно недемпфирован. Для систем с очень малым коэффициентом демпфирования и частотой возбуждения, близкой к резонансной частоте, установившиеся колебания могут стать очень большими.

Резонанс маятника

Для других приводимых в действие затухающих гармонических осцилляторов, уравнения движения которых не выглядят в точности как масса на примере пружины, резонансная частота остается

${\displaystyle \omega _{r}=\omega _{0}{\sqrt {1-2\zeta ^{2}}},}$

но определения ω₀ и ζ изменение на основе физики системы. Для маятника длины л и малый угол смещения θ, Уравнение (1) становится

${\displaystyle ml{\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}=F_{0}\sin(\omega t)-mg\theta -cl{\frac {\mathrm {d} \theta }{\mathrm {d} t}}}$

и поэтому

${\displaystyle \omega _{0}={\sqrt {\frac {g}{l}}},}$

${\displaystyle \zeta ={\frac {c}{2m}}{\sqrt {\frac {l}{g}}}.}$

Передаточная функция, частотная характеристика и резонанс для последовательной цепи RLC

Смотрите также: Цепь RLC § Последовательная цепь

Рисунок 1: Последовательная цепь RLC

• V, источник напряжения, питающий цепь
• я, ток, пропускаемый через цепь
• р, эффективное сопротивление комбинированной нагрузки, источника и компонентов
• L, индуктивность индуктор составная часть
• C, емкость конденсатор составная часть

Рассмотрим цепь состоящий из резистор с сопротивлением р, индуктор с индуктивностью L, а конденсатор с емкостью C соединены последовательно с током я(т) и ведомый Напряжение источник с напряжением v_в(т). Падение напряжения в цепи равно

${\displaystyle L{\frac {di(t)}{dt}}+Ri(t)+V(0)+{\frac {1}{C}}\int _{0}^{t}i(\tau )d\tau =v_{in}(t).}$

(4)

Вместо того, чтобы анализировать возможное решение этого уравнения, как в приведенном выше примере с пружиной, в этом разделе будет анализироваться частотная характеристика этой схемы. Принимая Преобразование Лапласа уравнения (4),

${\displaystyle sLI(s)+RI(s)+{\frac {1}{sC}}I(s)=V_{in}(s),}$

где я(s) и V_в(s) - преобразование Лапласа тока и входного напряжения соответственно, а s это сложный частотный параметр в области Лапласа. Переставляя сроки,

${\displaystyle I(s)={\frac {s}{s^{2}L+Rs+{\frac {1}{C}}}}V_{in}(s).}$

Резонанс напряжения на конденсаторе

Последовательная схема RLC предоставляет несколько вариантов измерения выходного напряжения. Предположим, что интересующее выходное напряжение - это падение напряжения на конденсаторе. Как показано выше, в области Лапласа это напряжение равно

${\displaystyle V_{out}(s)={\frac {1}{sC}}I(s)}$

или

${\displaystyle V_{out}={\frac {1}{LC(s^{2}+{\frac {R}{L}}s+{\frac {1}{LC}})}}V_{in}(s).}$

Определите для этой схемы собственную частоту и коэффициент демпфирования,

${\displaystyle \omega _{0}={\frac {1}{\sqrt {LC}}},}$

${\displaystyle \zeta ={\frac {R}{2}}{\sqrt {\frac {C}{L}}}.}$

Отношение выходного напряжения к входному становится равным

${\displaystyle H(s)\triangleq {\frac {V_{out}(s)}{V_{in}(s)}}={\frac {\omega _{0}^{2}}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}}$

ЧАС(s) это функция передачи между входным и выходным напряжением. Обратите внимание, что эта передаточная функция имеет два полюса –Корни многочлена в знаменателе передаточной функции – при

${\displaystyle s=-\zeta \omega _{0}\pm i\omega _{0}{\sqrt {1-\zeta ^{2}}}}$

(5)

и нет нули –Корни полинома в числителе передаточной функции. Кроме того, заметим, что для ζ ≤ 1, величина этих полюсов - собственная частота ω₀ и это для ζ < 1/${\displaystyle {\sqrt {2}}}$, наше условие резонанса в примере гармонического осциллятора, полюса ближе к мнимой оси, чем к действительной оси.

Оценка ЧАС(s) вдоль мнимой оси s = iω, передаточная функция описывает частотную характеристику этой схемы. Аналогично, частотную характеристику можно проанализировать, взяв преобразование Фурье уравнения (4) вместо преобразования Лапласа. Передаточная функция, которая также является сложной, может быть записана как усиление и фаза,

${\displaystyle H(i\omega )=G(\omega )e^{i\Phi (\omega )}.}$

График амплитуды Боде для напряжения на элементах последовательной цепи RLC. Собственная частота ω₀ = 1 рад / с, коэффициент демпфирования ζ = 0.4. Пиковое напряжение конденсатора ниже собственной частоты схемы, пиковое напряжение катушки индуктивности выше собственной частоты, а пиковое напряжение резистора - на собственной частоте с пиковым коэффициентом усиления, равным единице. Коэффициент усиления для напряжения на конденсаторе и катушке индуктивности, соединенных последовательно, показывает антирезонанс, причем коэффициент усиления стремится к нулю на собственной частоте.

Синусоидальное входное напряжение на частоте ω приводит к выходному напряжению с той же частотой, которая была масштабирована г(ω) и имеет фазовый сдвиг Φ(ω). Коэффициент усиления и фаза могут быть нанесены на график в зависимости от частоты. Сюжет Боде. Для напряжения конденсатора цепи RLC коэффициент усиления передаточной функции ЧАС(iω) является

${\displaystyle G(\omega )={\frac {\omega _{0}^{2}}{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}.}$

(6)

Обратите внимание на сходство между усилением здесь и амплитудой в уравнении (3). Еще раз, выигрыш максимален на резонансная частота

${\displaystyle \omega _{r}=\omega _{0}{\sqrt {1-2\zeta ^{2}}}.}$

Здесь резонанс физически соответствует наличию относительно большой амплитуды стационарных колебаний напряжения на конденсаторе по сравнению с его амплитудой на других частотах возбуждения.

Резонанс напряжения на катушке индуктивности

Резонансная частота не всегда должна иметь форму, приведенную в примерах выше. Для схемы RLC вместо этого предположим, что интересующее выходное напряжение - это напряжение на катушке индуктивности. Как показано выше, в области Лапласа напряжение на катушке индуктивности равно

${\displaystyle V_{out}(s)=sLI(s),}$

${\displaystyle V_{out}(s)={\frac {s^{2}}{s^{2}+{\frac {R}{L}}s+{\frac {1}{LC}}}}V_{in}(s),}$

${\displaystyle V_{out}(s)={\frac {s^{2}}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}V_{in}(s),}$

используя те же определения для ω₀ и ζ как в предыдущем примере. Передаточная функция между V_в(s) и этот новый V_вне(s) через катушку индуктивности

${\displaystyle H(s)={\frac {s^{2}}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}.}$

Обратите внимание, что эта передаточная функция имеет те же полюса, что и передаточная функция в предыдущем примере, но также имеет два нуля в числителе на s = 0. Оценка ЧАС(s) вдоль мнимой оси его коэффициент усиления равен

${\displaystyle G(\omega )={\frac {\omega ^{2}}{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}.}$

По сравнению с усилением в уравнении (6) используя напряжение конденсатора в качестве выхода, это усиление имеет коэффициент ω² в числителе и, следовательно, будет иметь другую резонансную частоту, которая максимизирует усиление. Эта частота

${\displaystyle \omega _{r}={\frac {\omega _{0}}{\sqrt {1-2\zeta ^{2}}}},}$

Таким образом, для той же цепи RLC, но с напряжением на катушке индуктивности в качестве выхода, резонансная частота теперь равна больше чем собственная частота, хотя она все еще стремится к собственной частоте, когда коэффициент демпфирования стремится к нулю. То, что одна и та же схема может иметь разные резонансные частоты для разных вариантов выхода, не противоречит. Как показано в уравнении (4) падение напряжения в цепи делится между тремя элементами схемы, и каждый элемент имеет разную динамику. Напряжение конденсатора медленно растет за счет интегрирования тока с течением времени и, следовательно, более чувствительно к более низким частотам, тогда как напряжение катушки индуктивности растет при быстром изменении тока и, следовательно, более чувствительно к более высоким частотам. В то время как цепь в целом имеет собственную частоту, на которой она имеет тенденцию к колебаниям, разная динамика каждого элемента схемы заставляет каждый элемент резонировать с немного другой частотой.^[7]

Резонанс напряжения на резисторе

Предположим, что интересующее выходное напряжение - это напряжение на резисторе. В области Лапласа напряжение на резисторе равно

${\displaystyle V_{out}(s)=RI(s),}$

${\displaystyle V_{out}(s)={\frac {Rs}{L(s^{2}+{\frac {R}{L}}s+{\frac {1}{LC}})}}V_{in}(s),}$

и используя ту же собственную частоту и коэффициент демпфирования, что и в примере конденсатора, передаточная функция равна

${\displaystyle H(s)={\frac {2\zeta \omega _{0}s}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}.}$

Обратите внимание, что эта передаточная функция также имеет те же полюса, что и предыдущие примеры схемы RLC, но у нее только один ноль в числителе на s = 0. Для этой передаточной функции ее коэффициент усиления равен

${\displaystyle G(\omega )={\frac {2\zeta \omega _{0}\omega }{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}.}$

Резонансная частота, которая максимизирует это усиление, равна

${\displaystyle \omega _{r}=\omega _{0},}$

и коэффициент усиления равен единице на этой частоте, поэтому напряжение на резисторе резонирует в собственная частота цепи, и на этой частоте амплитуда напряжения на резисторе равна амплитуде входного напряжения.

Антирезонанс

Основная статья: Антирезонанс

Некоторые системы показывают антирезонанс который можно анализировать так же, как резонанс. Для антирезонанса амплитуда отклика системы на определенных частотах непропорционально высока. маленький вместо того, чтобы быть непропорционально большим. В примере схемы RLC это явление можно наблюдать, анализируя как катушку индуктивности, так и конденсатор вместе.

Предположим, что интересующее выходное напряжение в цепи RLC - это напряжение на катушке индуктивности. и конденсатор соединен последовательно. Уравнение (4) показал, что сумма напряжений на трех элементах схемы суммируется с входным напряжением, поэтому измерение выходного напряжения как суммы напряжений на катушке индуктивности и конденсатора совпадает с v_в минус падение напряжения на резисторе. Предыдущий пример показал, что на собственной частоте системы амплитуда падения напряжения на резисторе равно амплитуда v_в, и поэтому напряжение на катушке индуктивности и конденсаторе вместе имеет нулевую амплитуду.Мы можем показать это с помощью передаточной функции.

Сумма напряжений индуктора и конденсатора равна

${\displaystyle V_{out}(s)=(sL+{\frac {1}{sC}})I(s),}$

${\displaystyle V_{out}(s)={\frac {s^{2}+{\frac {1}{LC}}}{s^{2}+{\frac {R}{L}}s+{\frac {1}{LC}}}}V_{in}(s).}$

Используя ту же собственную частоту и коэффициенты демпфирования, что и в предыдущих примерах, передаточная функция равна

${\displaystyle H(s)={\frac {s^{2}+\omega _{0}^{2}}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}.}$

Обратите внимание, что эта передача имеет те же полюса, что и предыдущие примеры, но имеет нули в

${\displaystyle s=\pm i\omega _{0}.}$

(7)

Оценивая передаточную функцию вдоль мнимой оси, ее коэффициент усиления равен

${\displaystyle G(\omega )={\frac {\omega _{0}^{2}-\omega ^{2}}{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}.}$

Вместо того чтобы искать резонанс, то есть пики усиления, обратите внимание, что усиление стремится к нулю при ω = ω₀, который дополняет наш анализ напряжения резистора. Это называется антирезонанс, что имеет противоположный эффект резонанса. Вместо того, чтобы давать непропорционально большие выходы на этой частоте, эта схема с таким выбором выхода вообще не реагирует на этой частоте.^[7] Частота, которая отфильтрована, точно соответствует нулям передаточной функции, которые были показаны в уравнении (7) и находились на мнимой оси.

Взаимосвязь между резонансом и частотной характеристикой в ​​примере последовательной цепи RLC

Эти примеры схем RLC иллюстрируют, как резонанс связан с частотной характеристикой системы. В частности, эти примеры иллюстрируют:

• Как можно найти резонансные частоты, ища пики усиления передаточной функции между входом и выходом системы, например, на графике амплитуды Боде
• Как резонансная частота для одной системы может отличаться для разных вариантов выхода системы
• Связь между собственной частотой системы, коэффициентом демпфирования системы и резонансной частотой системы
• Связь между собственной частотой системы и величиной полюсов передаточной функции, указанная в уравнении (5), и поэтому связь между полюсами и резонансной частотой
• Связь между нулями передаточной функции и формой усиления в зависимости от частоты, и, следовательно, связь между нулями и резонансной частотой, которая максимизирует усиление.
• Связь нулей передаточной функции с антирезонансом

В следующем разделе эти концепции распространяются на резонанс в общей линейной системе.

Обобщающий резонанс и антирезонанс для линейных систем

Затем рассмотрим произвольную линейную систему с несколькими входами и выходами. Например, в представление в пространстве состояний третий порядок линейная инвариантная во времени система с тремя входами и двумя выходами можно записать как

${\displaystyle {\begin{bmatrix}{\dot {x}}_{1}\\{\dot {x}}_{2}\\{\dot {x}}_{3}\end{bmatrix}}=A{\begin{bmatrix}x_{1}(t)\\x_{2}(t)\\x_{3}(t)\end{bmatrix}}+B{\begin{bmatrix}u_{1}(t)\\u_{2}(t)\\u_{3}(t)\end{bmatrix}},}$

${\displaystyle {\begin{bmatrix}y_{1}(t)\\y_{2}(t)\end{bmatrix}}=C{\begin{bmatrix}x_{1}(t)\\x_{2}(t)\\x_{3}(t)\end{bmatrix}}+D{\begin{bmatrix}u_{1}(t)\\u_{2}(t)\\u_{3}(t)\end{bmatrix}},}$

где ты_я(т) - входы, Икс_я(t) - переменные состояния, у_я(т) - выходы, а А, B, C, и D - матрицы, описывающие динамику между переменными.

Эта система имеет матрица передаточной функции элементы которого являются передаточными функциями между различными входами и выходами. Например,

${\displaystyle {\begin{bmatrix}Y_{1}(s)\\Y_{2}(s)\end{bmatrix}}={\begin{bmatrix}H_{11}(s)&H_{12}(s)&H_{13}(s)\\H_{21}(s)&H_{22}(s)&H_{23}(s)\end{bmatrix}}{\begin{bmatrix}U_{1}(s)\\U_{2}(s)\\U_{3}(s)\end{bmatrix}}.}$

Каждый ЧАС_ij(s) - скалярная передаточная функция, связывающая один из входов с одним из выходов. В приведенных выше примерах схемы RLC было одно входное напряжение и четыре возможных выходных напряжения - на конденсаторе, на катушке индуктивности, на резисторе и на конденсаторе и катушке индуктивности, соединенных последовательно, - каждое со своей передаточной функцией. Если бы схема RLC была настроена для измерения всех четырех из этих выходных напряжений, эта система имела бы матрицу передаточной функции 4 × 1, связывающую один вход с каждым из четырех выходов.

Оценивается по мнимой оси, каждый ЧАС_ij(iω) можно записать как коэффициент усиления и фазовый сдвиг,

${\displaystyle H_{ij}(i\omega )=G_{ij}(\omega )e^{i\Phi _{ij}(\omega )}.}$

Пики усиления на определенных частотах соответствуют резонансам между входом и выходом этой передаточной функции, предполагая, что система стабильный.

Каждая передаточная функция ЧАС_ij(s) также можно записать в виде дроби, числитель и знаменатель которой являются полиномами от s.

${\displaystyle H_{ij}(s)={\frac {N_{ij}(s)}{D_{ij}(s)}}.}$

Комплексные корни числителя называются нулями, а комплексные корни знаменателя - полюсами. Для стабильной системы положения этих полюсов и нулей на комплексной плоскости дают некоторое представление о том, может ли система резонировать или антирезонировать и на каких частотах. В частности, любой стабильной или незначительно стабильный комплексно сопряженная пара полюсов с мнимыми компонентами может быть записана в терминах собственной частоты и коэффициента затухания как

${\displaystyle s=-\zeta \omega _{0}\pm i\omega _{0}{\sqrt {1-\zeta ^{2}}},}$

как в уравнении (5). Собственная частота ω₀ этого полюса - величина положения полюса на комплексной плоскости, а коэффициент затухания этого полюса определяет, насколько быстро это колебание затухает. В общем,^[6]

• Комплексно сопряженные пары полюса около мнимой оси соответствуют пику или резонансу в частотной характеристике вблизи собственной частоты полюса. Если пара полюсов на На мнимой оси коэффициент усиления бесконечен на этой частоте.
• Комплексно сопряженные пары нули около мнимой оси соответствуют провалу или антирезонансу в частотной характеристике в окрестности частоты нуля, то есть частоты, равной величине нуля. Если пара нулей равна на На мнимой оси коэффициент усиления равен нулю на этой частоте.

В примере схемы RLC первое обобщение, связывающее полюса с резонансом, наблюдается в уравнении (5). Второе обобщение, связывающее нули с антирезонансом, наблюдается в уравнении (7). В примерах с гармоническим генератором, напряжением конденсатора цепи RLC и напряжением индуктора цепи RLC «полюса около мнимой оси» соответствуют условию значительно заниженного демпфирования ζ <1 /${\displaystyle {\sqrt {2}}}$.

Стоячие волны и резонанс непрерывных линейных систем

Основная статья: Стоячая волна

Физическая система может иметь столько собственных частот, сколько имеет степени свободы; каждая степень свободы может колебаться как гармонический осциллятор. Системы с одной степенью свободы, такие как масса на пружине и примеры цепей RLC, описанные ранее, имеют одну собственную частоту и могут резонировать около этой собственной частоты. Система более высокого порядка с двумя степенями свободы, например связанные маятники и резонансные трансформаторы, может иметь две собственные частоты и резонировать около каждой из этих частот. По мере увеличения числа связанных гармонических осцилляторов время, необходимое для передачи энергии от одного к другому, становится значительным. Системы с очень большим числом степеней свободы можно рассматривать как непрерывный а не как отдельные соединенные вместе осцилляторы. Энергия передается от одного осциллятора к другому в виде волн. Например, струна гитары или поверхность воды в чаше можно смоделировать как континуум небольших связанных осцилляторов, и волны могут перемещаться по ним. Во многих случаях эти системы могут резонировать на определенных частотах, образуя стоячие волны с колебаниями большой амплитуды в фиксированных положениях. Резонанс в форме стоячих волн лежит в основе многих известных явлений, таких как звук, производимый музыкальными инструментами, электромагнитные резонаторы, используемые в лазерах и микроволновых печах, и уровни энергии атомов.

Пример стоячих волн, описанных во многих вводных учебниках физики, - это случай стоячих волн на струне.^[8][9] Рассмотрим строку длины L который фиксируется с обоих концов. Струна может работать на любой частоте, заставляя волну этой частоты распространяться по струне, хотя мы увидим, что резонируют только определенные частоты. Волны от движущей силы отражать с концов струны, так что в конечном итоге достигается устойчивое состояние с волнами, распространяющимися в обоих направлениях вдоль струны. Волны мешать, поэтому форма волны, наблюдаемая на струне, является суммой или суперпозиция левых и правых бегущих волн.

Стоячие волны в струне - фундаментальный режим и первые 5 гармоники.

На определенных частотах возбуждения - в этом примере любая частота, которая делает длину струны целым числом полуволн - бегущие влево и вправо волны интерферируют особым образом, при этом в определенных фиксированных положениях струна никогда не смещается. Эти позиции называются узлами и включают два фиксированных конца. Между узлами струна совершает колебания большой амплитуды, которые не распространяются по струне. Ровно посередине между узлами колебания имеют наибольшую амплитуду, и эти положения называются анузлами.^[10]

Для струны с фиксированными концами в Икс = 0 и Икс = L, смещение струны можно записать как

${\displaystyle y(x,t)=2y_{\text{max}}\sin \left({2\pi x \over \lambda }\right)\cos(\omega t),}$

где

• у(Икс,т) - поперечное смещение струны как функция положения Икс и время т как волны растянуты,
• ω это угловая частота или эквивалентно 2π раз частота ж,
• λ это длина волны волны,
• Бегущие влево и вправо волны, мешающие формированию стоячей волны, имеют амплитуду у_{Максимум}.

Обратите внимание, что это волна, которая не распространяется. Он колеблется во времени с амплитудой, которая зависит от положения. Икс. Поскольку строка имеет конечную длину, только определенные частоты соответствуют правильному соотношению между длиной L и длина волны λ резонировать. Частоты, которые резонируют, можно записать как

${\displaystyle f={\frac {nv}{2L}},}$

${\displaystyle n=1,2,3,\ldots }$

где v - скорость волны по струне. Аналогично, длины волн, которые резонируют, можно записать как

${\displaystyle \lambda ={\frac {v}{f}}={\frac {2L}{n}},}$

${\displaystyle n=1,2,3,\ldots }$

Стоячая волна с п = 1 колеблется на основная частота и имеет длину волны, вдвое превышающую длину струны. Высшие целые значения п соответствуют режимам колебаний, называемым гармоники или обертоны. На рисунке выше показаны первые шесть режимов колебаний струны с двумя закрепленными концами.

Виды резонанса

Механический и акустический резонанс

Основные статьи: Механический резонанс, Акустический резонанс, и Струнный резонанс

Школьный эксперимент с резонирующей массой

Механический резонанс тенденция механическая система поглощать больше энергии, когда частота колебаний соответствует системному собственная частота из вибрация чем на других частотах. Это может вызвать резкие раскачивания и даже катастрофические разрушения неправильно построенных конструкций, включая мосты, здания, поезда и самолеты. При проектировании объектов инженеры должен гарантировать, что частоты механического резонанса компонентов не совпадают с частотами возбуждения двигателей или других колеблющихся частей, явление, известное как резонансная катастрофа.

Предотвращение резонансных катастроф - главная задача каждого здания, башни и мост строительство проект. В качестве контрмеры амортизаторы могут быть установлены для поглощения резонансных частот и, таким образом, для рассеивания поглощенной энергии. В Тайбэй 101 здание опирается на 660-тонный маятник (730 коротких тонн) —а настроенный массовый демпфер - погасить резонанс. Кроме того, конструкция спроектирована так, чтобы резонировать с частотой, которая обычно не встречается. Здания в сейсмический зоны часто строятся с учетом частот колебаний ожидаемых колебаний грунта. К тому же, инженеры проектирование объектов с двигателями должно гарантировать, что механические резонансные частоты составных частей не совпадают с частотами движущихся колебаний двигателей или других сильно колеблющихся частей.

Часы держать время за счет механического резонанса в балансир, маятник, или Кристалл кварца.

Было выдвинуто предположение, что частота вращения педалей бегунов является энергетически выгодной из-за резонанса между упругой энергией, запасенной в нижней конечности, и массой бегуна.^[11]

Акустический резонанс это филиал механический резонанс это связано с механическими колебаниями в диапазоне частот человеческого слуха, другими словами звук. У людей слух обычно ограничен частотами от 20 до 20.Гц и 20000 Гц (20кГц ),^[12] Многие предметы и материалы действуют как резонаторы с резонансными частотами в этом диапазоне и при ударе механически вибрируют, давя на окружающий воздух, создавая звуковые волны. Это источник многих перкуссионных звуков, которые мы слышим.

Акустический резонанс является важным фактором для производителей приборов, так как большинство акустических инструменты использовать резонаторы, такой как струны и тело скрипка, длина трубки в флейта формы и натяжения мембраны барабана.

Как и механический резонанс, акустический резонанс может привести к катастрофическому отказу объекта при резонансе. Классическим примером этого является разбивание бокала со звуком с точной резонансной частотой стакана, хотя на практике это сложно.^[13]

Электрический резонанс

Основная статья: Электрический резонанс

Анимация, иллюстрирующая электрический резонанс в настроенная схема, состоящий из конденсатор (C) и индуктор (L) соединены вместе. Заряд течет вперед и назад между пластинами конденсатора через катушку индуктивности. Энергия колеблется взад и вперед между конденсаторами. электрическое поле (E) и индуктора магнитное поле (B).

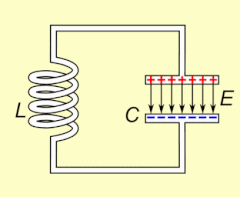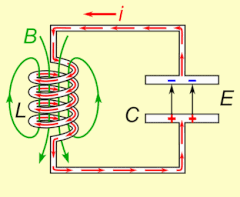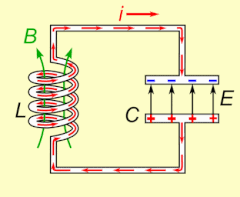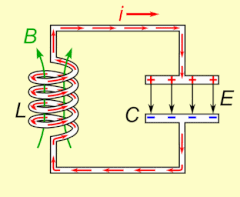
Электрический резонанс происходит в электрическая цепь на конкретном резонансная частота когда сопротивление цепи составляет минимум в последовательной цепи или максимум в параллельной цепи (обычно, когда функция передачи пики по абсолютной величине). Резонанс в схемах используется как для передачи, так и для приема беспроводной связи, такой как телевидение, сотовые телефоны и радио.^[14]

Оптический резонанс

Основная статья: Оптический резонатор

An оптический резонатор, также называемый оптический резонатор, представляет собой расположение зеркала что образует стоячая волна объемный резонатор для световые волны. Оптические резонаторы являются основным компонентом лазеры, окружающие получить средний и предоставление Обратная связь лазерного света. Они также используются в оптические параметрические генераторы и немного интерферометры. Свет, заключенный в полости, многократно отражается, создавая стоячие волны для определенных резонансных частот. Образцы стоячей волны называются «модами». Продольные моды отличаются только частотой, в то время как поперечные моды различаются для разных частот и имеют разные картины интенсивности по поперечному сечению луча. Кольцевые резонаторы и шепчущие галереи являются примерами оптических резонаторов, не образующих стоячие волны.

Разные типы резонаторов различаются фокусным расстоянием двух зеркал и расстоянием между ними; плоские зеркала используются нечасто из-за сложности их точного выравнивания. Геометрия (тип резонатора) должна быть выбрана так, чтобы луч оставался стабильным, то есть размер луча не продолжал расти с каждым отражением. Типы резонаторов также разработаны с учетом других критериев, таких как минимальная перетяжка луча или отсутствие фокальной точки (и, следовательно, интенсивного света в этой точке) внутри полости.

Оптические резонаторы рассчитаны на очень большую Q фактор.^[15] Луч отражается большое количество раз с небольшим затухание - поэтому частота ширина линии луча мала по сравнению с частотой лазера.

Дополнительные оптические резонансы волноводные резонансы и поверхностный плазмонный резонанс, что приводит к аномальному отражению и сильным затухающим полям при резонансе. В этом случае резонансные моды являются управляемыми модами волновода или поверхностными плазмонными модами границы раздела диэлектрик-металл. Эти моды обычно возбуждаются субволновой решеткой.

Орбитальный резонанс

Основная статья: Орбитальный резонанс

В небесная механика, орбитальный резонанс происходит, когда два вращающийся по орбите тела оказывают друг на друга регулярное периодическое гравитационное влияние, обычно из-за орбитальные периоды связаны соотношением двух маленьких целых чисел. Орбитальные резонансы значительно усиливают взаимное гравитационное влияние тел. В большинстве случаев это приводит к неустойчивый взаимодействие, при котором тела обмениваются импульсом и перемещаются по орбитам до тех пор, пока резонанс больше не существует. При некоторых обстоятельствах резонансная система может быть стабильной и самокорректирующейся, так что тела остаются в резонансе. Примеры: резонанс 1: 2: 4 Юпитер луны Ганимед, Европа, и Ио, и резонанс 2: 3 между Плутон и Нептун. Неустойчивые резонансы с Сатурн внутренние луны порождают пробелы в кольца Сатурна. Частный случай резонанса 1: 1 (между телами с одинаковыми радиусами орбиты) заставляет большие тела Солнечной системы очистить окрестности вокруг своих орбит, выбрасывая почти все остальное вокруг себя; этот эффект используется в текущем определение планеты.

Атомный, частичный и молекулярный резонанс

Основные статьи: Ядерный магнитный резонанс и Резонанс (физика элементарных частиц)

Магнит ЯМР в HWB-ЯМР, Бирмингем, Великобритания. В своем сильном 21,2-тесла поле протонный резонанс находится на частоте 900 МГц.

Ядерный магнитный резонанс (ЯМР) - это название явления физического резонанса, связанного с наблюдением определенных квантово-механический магнитный свойства атомный ядро в присутствии приложенного внешнего магнитного поля. Многие научные методы используют явления ЯМР для изучения молекулярная физика, кристаллы, и некристаллические материалы через ЯМР-спектроскопия. ЯМР также обычно используется в передовых медицинских методах визуализации, таких как магнитно-резонансная томография (МРТ).

Все ядра, содержащие нечетное число нуклоны иметь внутренний магнитный момент и угловой момент. Ключевой особенностью ЯМР является то, что резонансная частота конкретного вещества прямо пропорциональна силе приложенного магнитного поля. Именно эта функция используется в методах визуализации; если образец помещен в неоднородное магнитное поле, то резонансные частоты ядер образца зависят от того, где в поле они расположены. Следовательно, частицу можно довольно точно определить по ее резонансной частоте.

Электронный парамагнитный резонанс, иначе известный как электронный спиновой резонанс (ЭПР) - это спектроскопический метод, подобный ЯМР, но использующий вместо этого неспаренные электроны. Материалы, для которых это может быть применено, гораздо более ограничены, поскольку материал должен иметь непарное вращение и быть парамагнитный.

В Эффект Мёссбауэра резонансный и отдача -свободное выделение и поглощение гамма-луч фотоны атомами, связанными в твердой форме.

Резонанс в физике элементарных частиц появляется при аналогичных обстоятельствах классическая физика на уровне квантовая механика и квантовая теория поля. Однако их также можно рассматривать как нестабильные частицы, причем приведенная выше формула действительна, если Γ это скорость распада и Ω заменяется массой частицы M. В этом случае формула происходит от пропагатор, с заменой его массы на комплексное число M + iΓ. Формула также связана с величиной частицы скорость распада посредством оптическая теорема.

Добротность

Основная статья: Добротность

В Q фактор или фактор качества это безразмерный параметр, описывающий, как недостаточно демпфированный ан осциллятор или резонатор является,^[16] или, что эквивалентно, характеризует резонаторную пропускная способность относительно его центральной частоты.^[17]Высшее Q указывает на меньшую скорость потерь энергии по сравнению с запасенной энергией осциллятора, т.е. колебания затухают медленнее. Маятник, подвешенный на качественной опоре, колеблющийся в воздухе, имеет высокую Q, а погруженный в масло маятник имеет низкую Q. Чтобы поддерживать систему в резонансе с постоянной амплитудой за счет подачи энергии извне, энергия, выделяемая в каждом цикле, должна быть меньше, чем энергия, запасенная в системе (то есть сумма потенциальной и кинетической), на коэффициент Q/2π. Осцилляторы с добротными коэффициентами имеют низкую демпфирование, что заставляет их звонить дольше.

Синусоидально ведомый резонаторы имеющие более высокую добротность, резонируют с большими амплитудами (на резонансной частоте), но имеют меньший диапазон частот вокруг частоты, на которой они резонируют. Диапазон частот, на которых резонирует осциллятор, называется полосой пропускания. Таким образом, высокийQ настроенная схема в радиоприемнике было бы сложнее настроить, но у него было бы больше избирательность, он будет лучше фильтровать сигналы от других станций, находящихся поблизости в спектре. Генераторы с высокой добротностью работают в меньшем диапазоне частот и более стабильны. (Увидеть фазовый шум генератора.)

Добротность генераторов существенно различается от системы к системе. Системы, для которых важно демпфирование (например, демпферы, предохраняющие дверь от захлопывания), имеют Q = 1/2. Часы, лазеры и другие системы, которым необходим сильный резонанс или высокая стабильность частоты, нуждаются в высококачественных факторах. Камертоны иметь факторы качества вокруг Q = 1000. Добротность атомные часы и некоторые высокие-Q лазеры может достигать 10^11[18] и выше.^[19]

Физики и инженеры используют множество альтернативных величин для описания демпфирования осциллятора, которые тесно связаны с его добротностью. Важные примеры включают: коэффициент демпфирования, относительная пропускная способность, ширина линии, а пропускная способность измеряется в октавы.

Универсальная резонансная кривая

«Универсальная резонансная кривая», симметричное приближение к нормированному отклику резонансного контура; абсцисса значения представляют собой отклонение от центральной частоты в единицах центральной частоты, деленной на 2Q; ордината относительная амплитуда и фаза в циклах; пунктирные кривые сравнивают диапазон откликов реальных двухполюсных цепей на Q значение 5; для высшего Q значений меньше отклонение от универсальной кривой. Крестиками отмечены края полосы пропускания 3 дБ (усиление 0,707, фазовый сдвиг 45 ° или 0,125 цикла).

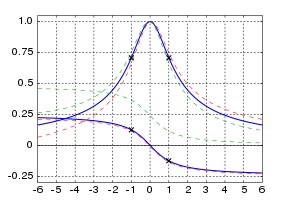
Точный отклик резонанса, особенно для частот, далеких от резонансной частоты, зависит от деталей физической системы и обычно не совсем симметричен относительно резонансной частоты, как показано для простой гармонический осциллятор выше. затухающий линейный генератор с резонансной частотой Ω, то интенсивность колебаний я когда система приводится в движение с частотой возбуждения ω обычно аппроксимируется формулой, симметричной относительно резонансной частоты:^[20]

${\displaystyle I(\omega )\equiv |\chi |^{2}\propto {\frac {1}{(\omega -\Omega )^{2}+\left({\frac {\Gamma }{2}}\right)^{2}}}.}$

Где восприимчивость ${\displaystyle \chi (\omega )}$ связывает амплитуду осциллятора с движущей силой в частотном пространстве:^[21]

${\displaystyle x(\omega )=\chi (\omega )F(\omega )}$

Интенсивность определяется как квадрат амплитуды колебаний. Это Функция Лоренца, или Распределение Коши, и этот отклик встречается во многих физических ситуациях, связанных с резонансными системами. Γ параметр, зависящий от демпфирование осциллятора и известен как ширина линии резонанса. Осцилляторы с сильным затуханием, как правило, имеют широкую ширину линии и реагируют на более широкий диапазон управляющих частот вокруг резонансной частоты. Ширина линии равна обратно пропорциональный к Q фактор, который является мерой резкости резонанса.

В радиотехника и электронная инженерия, этот примерный симметричный отклик известен как универсальная резонансная кривая, концепция, введенная Фредерик Э. Терман в 1932 г. для упрощения приближенного анализа радиосхем с диапазоном центральных частот и Q ценности.^[22][23]

Смотрите также

• Электронный портал
• Физический портал

• Акустический резонанс
• Антирезонанс
• Центральная частота
• Киматика
• Демпфирование
• Управляемое гармоническое движение
• Землетрясение
• Электрический резонанс
• Электрический дипольный спиновой резонанс
• Formant
• Гармонический осциллятор
• Импеданс
• Лимбический резонанс
• Нелинейный резонанс
• Параметрический осциллятор
• Положительный отзыв
• Добротность
• Резонансная катастрофа
• Резонатор
• Шумановский резонанс
• Простые гармонические колебания
• Стохастический резонанс
• Симпатическая строка
• Настроенная схема
• Вибрация

использованная литература

1. Кацухико Огата (2005). Системная динамика (4-е изд.). Университет Миннесоты. п. 617.
2. Аджой Гхатак (2005). Оптика, 3Е (3-е изд.). Тата МакГроу-Хилл. п. 6.10. ISBN  978-0-07-058583-6.
3. Резник и Холлидей (1977). Физика (3-е изд.). Джон Вили и сыновья. п. 324. ISBN  9780471717164. Имеется характерное значение частоты возбуждения ω " при котором амплитуда колебаний максимальна. Это состояние называется резонанс и ценность ω " при котором возникает резонанс, называется резонансная частота.
4. К.Юсуф Биллах и Роберт Х. Сканлан (1991). "Резонанс, разрушение моста через Такома и учебники по физике для студентов" (PDF). Американский журнал физики. 59 (2): 118–124. Bibcode:1991AmJPh..59..118B. Дои:10.1119/1.16590. Получено 2011-05-29.
5. Оберг, Джеймс (4 февраля 2009 г.). "НАСА сотрясает космическую станцию". Новости NBC.
6. Хардт, Дэвид (2004). «Понимание полюсов и нулей» (PDF). Кафедра машиностроения. 2.14. Анализ и проектирование систем управления с обратной связью. Массачусетский Институт Технологий. Получено 18 апреля, 2020.
7. Чивер, Эрик. «Что нужно знать о поведении системы». Swarthmore College. Получено 18 апреля, 2020.
8. Холлидей, Дэвид; Резник, Роберт; Уокер, Джерл (2005). Основы физики (7-е изд.). Джон Вили и сыновья. п. 434. ISBN  0-471-42959-7.
9. Serway, Raymond A .; Фаун, Джерри С. (1992). Колледж физики (3-е изд.). Издательство колледжа Сондерс. п. 475-476. ISBN  0-03-076377-0.
10. Струнный резонанс. Цифровой звук и музыка. 21 мая 2014 г. Идентификатор видео на YouTube: oZ38Y0K8e-Y. Получено 22 августа, 2020.
11. Снайдер; Фарли (2011). «Энергетически оптимальная частота шагов в беге: эффекты наклона и снижения». Журнал экспериментальной биологии. 214 (12): 2089–95. Дои:10.1242 / jeb.053157. PMID  21613526.
12. Гарри Ф. Олсон Музыка, физика и инженерия. Dover Publications, 1967, стр. 248–249. «В очень благоприятных условиях большинство людей могут получить тональные характеристики до 12 Гц».
13. "Разбить стекло звуком". Лаборатория учебных ресурсов. UCLA Физика и астрономия.
14. "Физика резонанса". Интуитор. Получено 10 июля 2017.
15. Энциклопедия лазерной физики и техники - Q коэффициент, добротность, полость, резонатор, генератор, стандарты частоты
16. Джеймс Х. Харлоу (2004). Электроэнергетическая трансформаторная техника. CRC Press. С. 2–216. ISBN  978-0-8493-1704-0.
17. Майкл Х. Тули (2006). Электронные схемы: основы и приложения. Newnes. С. 77–78. ISBN  978-0-7506-6923-8.
18. Энциклопедия лазерной физики и техники: Q фактор
19. Время и частота от А до Я: от Q до Ra В архиве 2008-05-04 на Wayback Machine
20. А. Э. Сигман (1986). Лазеры. Книги университетских наук. стр.105 –108. ISBN  978-0-935702-11-8. резонансная аппроксимация амплитуда ширина линии частота лоренцевы вещественные числа.
21. Аспельмейер М .; и другие. (2014). «Полостная оптомеханика». Обзор современной физики. п. 1397.
22. Фредерик Эммонс Терман (1932). Радиотехника. Книжная компания McGraw-Hill. терман фредерик универсал.
23. Уильям МакКи. Зиберт (1986). Цепи, сигналы и системы. MIT Press. п. 113. ISBN  978-0-262-19229-3.

внешние ссылки

• Определение резонанса - «Увеличение амплитуды колебаний электрической или механической системы, подверженной действию периодической силы, частота которой равна или очень близка к собственной незатухающей частоте системы».
• Резонанс - глава из онлайн-учебника
• Грин, Брайан, "Резонанс в струнах ". Элегантная Вселенная, НОВАЯ ЗВЕЗДА (PBS )
• Раздел гиперфизики, посвященный концепциям резонанса
• Резонанс против резонансного (использование терминов)
• Деревянный и воздушный резонанс в клавесине
• Java-апплет демонстрация резонансов на струне при изменении частоты движущей силы
• Java-апплет демонстрация возникновения резонанса, когда частота возбуждения совпадает с собственной частотой генератора
• Бьющееся стекло со звуком, включая высокоскоростные кадры разбития стекла