Калькулятор паскалей - Pascals calculator

Паскалин, подписанный Паскалем в 1652 году

Вид сверху и обзор всего механизма^[1]

Калькулятор Паскаля (также известный как арифметическая машина или же Паскалин) это механический калькулятор изобретен Блез Паскаль в середине 17 века. Паскаль был вынужден разработать калькулятор путем кропотливых арифметических вычислений, необходимых для работы его отца в качестве налогового инспектора в стране. Руан.^[2] Он разработал машину для прямого сложения и вычитания двух чисел, а также для выполнения умножения и деления путем повторного сложения или вычитания.

Калькулятор Паскаля оказался особенно успешным в разработке своего механизм переноски, который добавляет 1 к 9 на одном циферблате и переносит 1 на следующий циферблат, когда первый циферблат изменяется с 9 на 0. Его нововведение сделало каждую цифру независимой от состояния других, что позволило нескольким переносам быстро переходить от одной цифры к другой независимо от мощности машины. Паскаль был также первым, кто сжал и адаптировал для своих целей фонарь, используется в турельные часы и водяные колеса. Это нововведение позволило устройству выдерживать любые действия оператора с очень небольшим дополнительным трением.

Паскаль сконструировал машину в 1642 году.^[3] После 50 прототипы, он представил устройство публике в 1645 году, посвятив его Пьер Сегье, тогда канцлер Франции.^[4] В течение следующего десятилетия Паскаль построил еще около двадцати машин, многие из которых улучшили его первоначальную конструкцию. В 1649 году король Людовик XIV Франции дал Паскалю королевская привилегия (аналогично патент ), что дало исключительное право на разработку и производство вычислительных машин во Франции. В настоящее время существует девять калькуляторов Pascal;^[5] большинство из них выставлено в европейских музеях.

Многие более поздние калькуляторы были либо непосредственно вдохновлены, либо сформированы теми же историческими влияниями, которые привели к изобретению Паскаля. Готфрид Лейбниц изобрел его Колеса Лейбница после 1671 г., после попытки добавить в Паскалин функцию автоматического умножения.^[6] В 1820 г. Томас де Кольмар разработал его арифмометр, первый механический калькулятор, достаточно прочный и надежный для повседневного использования в офисе. Неясно, видел ли он когда-нибудь устройство Лейбница, но он либо заново изобрел его, либо использовал изобретение Лейбница ступенчатого барабана.

История

Четыре Паскалина и клон Лепина на выставке в музее CNAM в Париже

Паскаль начал работать над своим калькулятором в 1642 году, когда ему было 19 лет. Он помогал своему отцу, который работал налоговым инспектором, и стремился создать устройство, которое могло бы снизить часть его рабочей нагрузки. Паскаль получил Королевская привилегия в 1649 году, что дало ему исключительные права на производство и продажу вычислительных машин во Франции.

К 1654 году он продал около двадцати машин, но стоимость и сложность Pascaline были препятствием для дальнейших продаж, и в том же году производство было прекращено. К тому времени Паскаль перешел к изучению религия и философия, что дало нам Lettres provinciales и Pensées.

Празднование трехсотлетия изобретения Паскаля механического калькулятора произошло во время Второй мировой войны, когда Франция была оккупирована Германией, и поэтому главное празднование проходило в Лондоне, Англия. В выступлениях, произнесенных на мероприятии, были отмечены практические достижения Паскаля, когда он уже был известен в области чистой математики, и его творческое воображение, а также то, насколько опередили свое время и машина, и ее изобретатель.^[7]

Дизайн

Деталь механизма переноски и сотуар

Колесо ввода

Калькулятор имел металлические колесные диски со спицами, с цифрами от 0 до 9, отображаемыми по окружности каждого колеса. Чтобы ввести цифру, пользователь поместил стилус в соответствующее пространство между спицами и повернул циферблат до металлического упора внизу, аналогично тому, как поворотный циферблат телефона используется. Это отобразило число в окнах в верхней части калькулятора. Затем нужно было просто повторно набрать второе число, которое нужно добавить, в результате чего сумма обоих чисел появилась в аккумуляторе.

Каждый циферблат связан с однозначным окном дисплея, расположенным прямо над ним, которое отображает значение аккумулятора для этой позиции. Дополнение к этой цифре в основании колеса (6, 10, 12, 20) отображается непосредственно над этой цифрой. Горизонтальная полоса скрывает либо все дополнительные числа, когда она перемещена вверх, либо все прямые числа, когда она перемещается к центру машины. Таким образом, он отображает либо содержимое аккумулятора, либо дополнение его значения.

Поскольку шестерни калькулятора вращались только в одном направлении, отрицательные числа нельзя было напрямую суммировать. Чтобы вычесть одно число из другого, метод девять дополнений использовался. Единственные два различия между сложением и вычитанием - это положение полоски дисплея (прямое или дополнение) и способ ввода первого числа (прямое или дополнительное).

Для 10-значного колеса (N) фиксированное внешнее колесо пронумеровано от 0 до 9 (N-1). Числа вписаны в убывающем образом по часовой стрелке, идущей от левого нижнего угла в правый нижний стоп рычага. Чтобы добавить 5, нужно вставить стилус между спицами, которые окружают цифру 5, и повернуть колесо по часовой стрелке до упора. Число, отображаемое в соответствующем регистре дисплея, будет увеличено на 5, и, если происходит перенос переноса, регистр дисплея слева от него будет увеличен на 1. Чтобы добавить 50, используйте колесо ввода десятков (второе колесо от прямо на десятичной машине), чтобы добавить 500, используйте колесо ввода сотен и т. д.

На всех колесах всех известных машин, кроме машина поздняя,^[8] отмечены две соседние спицы; эти знаки различаются от машины к машине. На колесе, изображенном справа, высверлены точки, на геодезическом станке они вырезаны; некоторые - это просто царапины или следы от лака,^[9] некоторые были даже помечены маленькими бумажками.^[10]

Эти метки используются для установки максимального числа соответствующего цилиндра, готового к повторной установке нуля. Для этого оператор вставляет иглу между этими двумя спицами и поворачивает колесо до упора. Это работает, потому что каждое колесо напрямую связано с соответствующим цилиндром дисплея (оно автоматически поворачивается на одно во время операции переноса). Чтобы пометить спицы во время изготовления, можно переместить цилиндр так, чтобы отображался его наибольший номер, а затем пометить спицу под стопорным рычагом и ту, которая находится справа от него.

Четыре из известных машин имеют внутренние колеса дополнений, которые использовались для ввода первого операнда при вычитании. Они установлены в центре каждого металлического колеса со спицами и вращаются вместе с ним. Колесо, показанное на картинке выше, имеет внутреннее колесо дополнений, но числа, написанные на нем, едва видны. На десятичной машине цифры от 0 до 9 вырезаны по часовой стрелке, причем каждая цифра расположена между двумя спицами, так что оператор может напрямую вписать ее значение в окно дополнений, поместив свой стилус между ними и повернув колесо по часовой стрелке до упора. до остановки рычага.^[11] В отметки на двух соседних спицах по бокам цифры 0, начертанной на этом колесе.

На четырех известных машинах над каждым колесом на индикаторной полосе установлено небольшое колесо частного. Эти частные колеса, которые устанавливаются оператором, имеют числа от 1 до 10, нанесенные по часовой стрелке на их периферии (даже над недесятичным колесом). Кажется, что во время деления использовались частные колеса, чтобы запомнить, сколько раз вычитался делитель для каждого данного индекса.^[12]

Внутренний механизм

Фонарь, используемый в турельных часах, приводимый в движение гирями, которые могут весить сотни килограммов.

Адаптация Паскаля. Синяя шестерня (входная) находится в зацеплении с желтыми шестернями (обработка), которые сами приводят в движение красную шестерню (выходную). Пересечение двух перпендикулярных цилиндров составляет одну точку, и поэтому теоретически синяя шестерня и желтая шестерня зацепляются в одной точке. Паскаль разработал механизм, который мог легко взять на себя силу самого сильного оператора и при этом добавить почти нулевое трение ко всему механизму.

Паскаль прошел через 50 прототипов, прежде чем остановился на своем окончательном проекте; мы знаем, что он начал с какого-то механизма счетных часов, в котором использовались пружины, которые, очевидно, «работают как пружины и имеют очень простую конструкцию», использовались «много раз» и оставались в «рабочем состоянии». Тем не менее, «постоянно улучшая ее», он нашел причину попытаться сделать всю систему более надежной и устойчивой.^[13] В конце концов он принял компонент очень больших часов, уменьшив и приспособив для своих целей надежные шестерни, которые можно найти в часовом механизме револьверной головки, называемом фонарь, сам производный от механизма водяного колеса. Это может легко справиться с силой ввода оператора.^[14]

Паскаль приспособил собачку и храповой механизм к своей собственной конструкции башенного колеса; защелка предотвращает вращение колеса против часовой стрелки во время ввода данных оператором, но она также используется для точного позиционирования колеса дисплея и механизма переноса следующей цифры, когда оно поднимается и приземляется в свое следующее положение. Благодаря этому механизму каждое отображаемое число идеально центрируется в окне дисплея, и каждая цифра точно позиционируется для следующей операции. Этот механизм будет перемещен шесть раз, если оператор наберет шесть на соответствующем колесе ввода.

Механизм переноски

Сотуар

Сотуар - центральная часть механизма переноски паскалина. В его "Avis nécessaire ... ", Паскаль отметил, что машина с 10 000 колесами будет работать так же хорошо, как и машина с двумя колесами, потому что каждое колесо не зависит от другого. Когда пришло время распространять перенос, сотуар, исключительно под действием силы тяжести,^[15] бросается к следующему колесу без какого-либо контакта между колесами. Во время свободного падения сотуар ведет себя как акробат, перепрыгивающий с одной трапеции на другую, при этом трапеции не касаются друг друга («сотуар» происходит от французского глагола соте, что означает прыгать). Следовательно, все колеса (включая шестерни и сотуар) имеют одинаковый размер и вес независимо от мощности машины.

Паскаль использовал гравитацию, чтобы вооружить сотуары. Чтобы полностью взвести сотуар, нужно повернуть колесо на пять шагов от 4 до 9, но передача переноса перемещает следующее колесо только на один шаг. Таким образом, при включении сотуара накапливается много дополнительной энергии.

Все сотуары активируются либо оператором, либо переносом. Чтобы обнулить машину с 10 000 колесами, если таковая существует, оператор должен будет установить каждое колесо на максимум, а затем прибавить 1 к «единичному» колесу. Переносчик поворачивал каждое колесо ввода одно за другим очень быстро. эффект домино мода и все регистры дисплея были бы сброшены.

Три фазы операции переноса

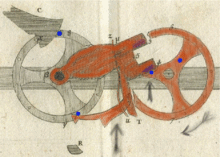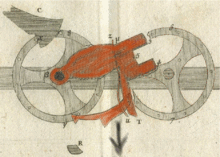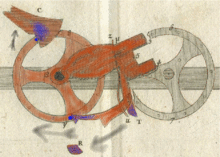
Передача переноса имеет три фазы:

1. Первая фаза происходит, когда регистр дисплея переходит от 4 к 9. Два штифта для переноски (один за другим) поднимают сотуар, нажимая на его выступающую часть, отмеченную (3,4,5). В то же время пинки собачка (1) поднимается вверх, используя штифт на принимающем колесе в качестве направляющей, но без воздействия на это колесо из-за верхней собачка / трещотка (C). Во время первой фазы активное колесо касается того, которое будет принимать перенос через сотуар, но оно никогда не перемещает и не изменяет его, и, следовательно, статус принимающего колеса не оказывает никакого влияния на активное колесо.
2. Вторая фаза начинается, когда регистр дисплея переходит от 9 до 0. Собачка проходит через направляющий штифт и весна (z, u) помещает его над этим штифтом, готовый надавить на него. Сотуар продолжает двигаться вверх, и вдруг его роняет вторая булавка для переноски. Сотуар падает под собственным весом. На втором этапе сотуар и два колеса полностью отключены.
3. Удар ногой собачка (1) толкает штифт на принимающее колесо и начинает его вращать. Верхний собачка / трещотка (C) перемещается в следующее пространство. Работа останавливается, когда выступающий часть (T) попадает в буферный упор (R). Верхний собачка / трещотка (C) позиционирует весь приемный механизм на свое место. Во время третьей фазы сотуар, который больше не касается активного колеса, добавляет единицу к принимающему колесу.

Операция

Pascaline - это машина прямого суммирования (у него нет кривошипа), поэтому значение числа добавляется в аккумулятор по мере его набора. Перемещая полосу дисплея, оператор может увидеть либо число, хранящееся в калькуляторе, либо дополнение его стоимости. Вычитание выполняется как сложение с использованием некоторых свойств Дополнение 9 арифметика.

Дополнение 9

Дополнение до 9 любого однозначного десятичного числа d это 9-d. Таким образом, дополнение 9 до 4 равно 5, а дополнение 9 до 0 равно 0. Точно так же дополнение до 3 до 11 равно 8.

В десятичном автомате, где n набирает дополнение до 9 числа A:

${\displaystyle CP(A)=10^{n}-1-A}$

и, следовательно, дополнение (A-B) до 9:

${\displaystyle {\begin{aligned}CP(A-B)&=10^{n}-1-(A-B)\\&=10^{n}-1-A+B\\&=CP(A)+B\end{aligned}}}$

Другими словами, дополнение до девятки разности двух чисел равно сумме девятого дополнения минуемого, добавленного к вычитаемому. Тот же принцип действует и может использоваться с числами, состоящими из цифр с различным основанием (основание 6, 12, 20), как в геодезических или бухгалтерских машинах.

Это также может быть расширено на:

${\displaystyle CP(A-B-C-D)=CP(A)+B+C+D}$

Этот принцип применим к пасталину:

${\displaystyle CP(A)}$	Сначала вводится дополнение уменьшаемого. Оператор может использовать внутренние колеса комплектующих или наберите дополнение к уменьшаемому напрямую. Полоса отображения сдвигается, чтобы показать окно дополнения, так что оператор видит отображаемый прямой номер, потому что ${\displaystyle CP(CP(A))=A}$.
B	Затем набирается второе число и добавляется его значение в аккумулятор.
${\displaystyle CP(A-B)}$	Результат (A-B) отображается в окне дополнения, потому что ${\displaystyle CP(CP(A-B))=A-B}$. Последний шаг можно повторять до тех пор, пока вычитаемое меньше, чем вычитаемое, отображаемое в аккумуляторе.

Сброс машины

Перед каждой новой операцией машину необходимо обнулять. Чтобы перезагрузить машину, оператор должен установить все колеса на максимум, используя отметки на двух соседних спицах, а затем добавьте 1 к крайнему правому колесу.^[16]

Выбранный Паскалем метод повторного обнуления, который распространяет перенос на всю машину, является наиболее сложной задачей для механического калькулятора и перед каждой операцией доказывает, что машина полностью работоспособна. Это свидетельство качества Pascaline, потому что ни в одной из критических замечаний 18-го века к машине не упоминалось о проблеме с механизмом переноски, и тем не менее эта функция была полностью протестирована на всех машинах с их перезагрузкой все время.^[17]

Пере-ноль	Установите все колеса на максимум, используя метки на двух соседних спицах. Каждое колесо готово к транспортировке.	0   0   0   0   0   9   9   9   9   9
	Добавьте 1 к крайнему правому колесу. Каждое колесо отправляет свой сотуар следующему, нули появляются один за другим, как в эффекте домино, справа налево.	9   9   9   9   9   0   0   0   0   0

Добавление

Добавления выполняются при перемещении полосы дисплея ближе всего к краю машины, отображающей непосредственное значение аккумулятора.

После обнуления автомата номера набираются один за другим.

В следующей таблице показаны все шаги, необходимые для вычисления 12,345 + 56,789 = 69,134.

Добавление	Машина на нуле, оператор вводит 12 345.	8   7   6   5   4   1   2   3   4   5
	Оператор вводит второй операнд: 56,789. Если он начинает с крайнего правого числа, второе колесо переместится с 4 на 5 во время записи 9 из-за передачи переноса ....	3   0   8   6   5   6   9   1   3   4

Вычитание

Вычитания выполняются с перемещением полосы дисплея ближе всего к центру машины, показывающей значение дополнения аккумулятора.

Аккумулятор содержит ${\displaystyle CP(A)}$ на первом этапе и ${\displaystyle CP(A-B)}$ после добавления B. При отображении этих данных в дополнительном окне оператор видит ${\displaystyle CP(CP(A))}$ который является A, а затем ${\displaystyle CP(CP(A-B))}$ который ${\displaystyle (A-B)}$. Это похоже на добавление, поскольку единственные два различия между сложением и вычитанием - это положение полосы отображения (прямое или дополнение) и способ ввода первого числа (прямое или дополнительное).

В следующей таблице показаны все шаги, необходимые для вычисления 54 321-12 345 = 41 976

Изменить пространство дисплея	Переместите полоску дисплея вниз, чтобы открыть дополнительную часть каждого цилиндра результата. С этого момента каждое число, набранное в автомате, добавляет свое значение в аккумулятор и, следовательно, уменьшает общее количество, отображаемое в окне дополнения.	9   9   9   9   9   0   0   0   0   0
Вычитание	Введите дополнение к девятке. Оператор может использовать внутренние колеса комплектующих или наберите цифру 54 321 (45 678) напрямую.	5   4   3   2   1   4   5   6   7   8
	Наберите вычитаемое (12 345) на металлических колесах со спицами. Это дополнение. Результат, 41 976, находится в окне дополнения до 9.	4   1   9   7   6   5   8   0   2   3

Использует

Паскалины вошли в оба десятичный и недесятичные разновидности, которые сегодня можно увидеть в музеях. Они были разработаны для использования учеными, бухгалтерами и геодезистами. Самый простой Паскалин имел пять циферблатов; более поздние варианты имели до десяти циферблатов.

Современный Французская валюта используемая система ливры, золы и отрицатели с 20 золы к ливр и 12 отрицатели к соль. Длина измерялась в туаз, пестрые, пакеты и Lignes с 6 пестрые к качать, 12 пакеты к пестрый и 12 Lignes к мешок. Следовательно, паскалину нужны колеса с основанием 6, 10, 12 и 20. Недесятичные колеса всегда располагались перед десятичной частью.

В бухгалтерской машине (..10,10,20,12) десятичная часть считала количество ливры (20 золы), золы (12 отрицатели) и отрицатели. В геодезической машине (..10,10,6,12,12) десятичная часть считала количество туаз (6 пестрые), пестрые (12 пакеты), пакеты (12 Lignes) и LignesУ научных машин просто были десятичные колеса.

Конфигурации

Тип аппарата	Другие колеса	4-й	3-й	2-й	1-й
Десятичный / научный	база 10 Десять тысяч	база 10 Тысячи	база 10 Сотни	база 10 Десятки	база 10 Единицы
Бухгалтерский учет	база 10 Сотни	база 10 Десятки	база 10 Ливр	база 20 Sols	база 12 Отрицатели
Геодезия	база 10 Десятки	база 10 Toises	база 6 Pieds	база 12 Пакеты	база 12 Lignes

Десятичная часть каждой машины выделяется.

Метрическая система была принята во Франции 10 декабря 1799 года, когда основной дизайн Паскаля вдохновил других мастеров, хотя и не имел такого же коммерческого успеха.

Производство

Большинство машин, уцелевших веками, относятся к учетному типу. Семь из них находятся в европейских музеях, один принадлежит корпорации IBM и один находится в частных руках.

Место расположения	Страна	Имя машины	Тип	Колеса	Конфигурация	Примечания
Музей CNAM Париж	Франция	Chancelier Séguier	Бухгалтерский учет	8	6 х 10 + 20 + 12
Музей CNAM Париж	Франция	Кристина, королева Швеции	Научный	6	6 х 10
Музей CNAM Париж	Франция	Луи Перье	Бухгалтерский учет	8	6 х 10 + 20 + 12	Луи Перье, племянник Паскаля, предложил его Академия наук Парижа в 1711 г.
Музей CNAM Париж	Франция	Поздно (Поздно)	Бухгалтерский учет	6	4 х 10 + 20 + 12	Эта машина была собрана в 18 веке с неиспользованными деталями.[18]
MuséeАнри Лекок[19] Клермон-Ферран	Франция	Маргерит Перье	Научный	8	8 х 10	Маргарита (1646–1733) была крестницей Паскаля.[20]
Musée Henri Lecoq Клермон-Ферран	Франция	Шевалье Дюрант-Паскаль	Бухгалтерский учет	5	3 х 10 + 20 + 12	Это единственная известная машина, которая поставлялась с коробкой. Это самая маленькая машина. Это должно было быть портативным?
Математико-физический салон,[21] Дрезден	Германия	Королева Польши	Бухгалтерский учет	10	8 х 10 + 20 + 12	Второе колесо справа имеет колесо с 10 спицами, содержащееся в неподвижном колесе с 20 сегментами. Это могло быть связано с плохой реставрацией.
Коллекция Léon Parcé	Франция		Геодезия	8	5 х 10 + 6 + 12 + 12	Эта машина была куплена как сломанная музыкальная шкатулка во французском антикварном магазине в 1942 году.
IBM коллекция[22]	Соединенные Штаты Америки		Бухгалтерский учет	8	6 х 10 + 20 + 12

Достижения

Паскалин сделал для французской валюты, которая когда-то принадлежала Луи Перье, племяннику Паскаля. Наименее значимые купюры, золы и отрицатели, находятся справа

Вид сзади калькулятора, показывающий колеса

Помимо того, что это первая вычислительная машина, обнародованная в свое время, Pascaline также:

• единственный действующий механический калькулятор в 17 веке
• первый калькулятор с механизмом управляемого переноса, позволяющий эффективно распространять несколько переносов^[23]
• первый калькулятор, который будет использоваться в офисе (его отец для расчета налогов)
• первый коммерческий калькулятор (было построено около двадцати машин)^[5]
• первый запатентованный калькулятор (королевская привилегия 1649 г.)^[24]
• первый калькулятор, описанный в энциклопедия (Дидро и Даламбер, 1751 г.)^[25]
• первый калькулятор, проданный дистрибьютором^[26]

Конкурирующие проекты

Счетные часы Шикарда

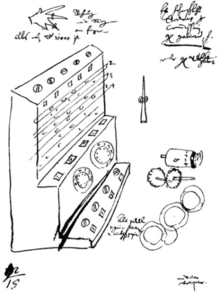
В 1957 году Франц Хаммер, биограф Иоганн Кеплер, объявил об обнаружении двух букв, которые Вильгельм Шикард написал своему другу Иоганну Кеплеру в 1623 и 1624 годах, который содержит чертежи ранее неизвестных рабочих счетных часов, предшествующих работе Паскаля на двадцать лет.^[27] В письме 1624 года говорилось, что первая машина, которую должен был построить профессионал, была уничтожена пожаром во время ее постройки, и что он отказывался от своего проекта.^[28] После тщательного изучения было обнаружено, что противоречит пониманию Франца Хаммера, что рисунки Шикарда публиковались не реже одного раза в столетие, начиная с 1718 года.^[29]

Бруно фон Фрейтаг Лорингхофф, профессор математики Тюбингенский университет построил первую копию машины Шикарда, но не без добавления колес и пружин для завершения дизайна.^[30] Эта деталь не описана в двух сохранившихся письмах и рисунках Шикарда. Проблема в работе машины Шикарда, судя по сохранившимся записям, была обнаружена после создания реплик.^[31] В машине Шикарда использовались часовые колеса, которые были сделаны прочнее и, следовательно, тяжелее, чтобы предотвратить их повреждение под действием усилия оператора. Каждая цифра использовала колесо отображения, колесо ввода и промежуточное колесо. Во время переноса все эти колеса сцепились с колесами пальца, принимающего перенос. Суммарное трение и инерция всех этих колес может «... потенциально повредить машину, если перенос должен передаваться по цифрам, например, как прибавление 1 к числу вроде 9999».^[32] Большим нововведением в калькуляторе Паскаля было то, что он был спроектирован таким образом, что каждое колесо ввода полностью независимо от всех остальных, и переносы распространяются последовательно. Паскаль выбрал для своей машины метод повторного обнуления, который распространяет перенос прямо через машину.^[16] Это самая сложная операция для механического калькулятора, и перед каждой операцией доказывается, что механизм переноса Pascaline полностью исправен. Это можно рассматривать как свидетельство качества Pascaline, потому что ни в одной из критических замечаний 18-го века к машине не упоминалось о проблеме с механизмом переноски, и тем не менее эта функция была полностью протестирована на всех машинах путем их перезапуска все время.^[17]

Рисунок Лейбница, на котором 365 умножено на 124.

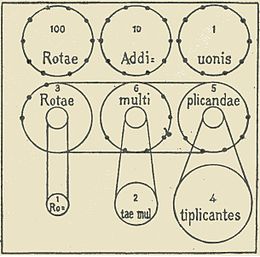
Готфрид Лейбниц начал работать над собственным калькулятором после смерти Паскаля. Сначала он попытался построить машину, которая могла бы автоматически размножаться, сидя на вершине Паскалина, предполагая (ошибочно), что все шкалы на калькуляторе Паскаля могут работать одновременно. Несмотря на то, что это невозможно было сделать, это был первый случай, когда вертушка была описана и использована на чертеже калькулятора.

Затем он разработал конкурирующий дизайн - Ступенчатый счетчик который был предназначен для автоматического выполнения сложения, вычитания и умножения, а также деления под управлением оператора. Лейбниц сорок лет пытался усовершенствовать эту конструкцию и изготовил две машины: одну в 1694 году и одну в 1706 году.^[33] Известно, что существует только машина 1694 года постройки; он был вновь открыт в конце 19 века, проведя 250 лет в забвении на чердаке в Геттингенский университет.^[33]

Немецкого изобретателя вычислительной машины Артура Буркхардта попросили попытаться привести машину Лейбница в рабочее состояние. Его отчет был благоприятным, за исключением последовательности в переносе.^[34] и «поэтому, особенно в случае множественных переносов, оператор должен был проверить результат и вручную исправить возможные ошибки».^[35] Лейбницу не удалось создать калькулятор, который работал бы должным образом, но он изобрел Колесо лейбница, принцип двухходового механического вычислителя. Он также был первым, у кого появились курсоры для записи первого операнда и подвижная тележка для результатов.

Было пять дополнительных попыток создания вычислительных машин с «прямым входом» в 17 веке (включая конструкции Тито Бураттини, Сэмюэл Морланд и Рене Грийе ).

Около 1660 года Клод Перро сконструировал abaque rhabdologique его часто принимают за механический калькулятор, потому что в нем есть механизм переноса между числами. Но на самом деле это счеты, поскольку они требуют, чтобы оператор по-разному обращался со станком, когда происходит перенос.^[36]

Калькулятор Паскаля был самым успешным механическим калькулятором, разработанным в 17 веке для сложения и вычитания больших чисел. У ступенчатого счетчика возникла проблема в механизме переноса после более чем двух последовательных переносов, а другие устройства имели механизмы переноса (одно зубчатое колесо), которые были ограничены в их способности переносить несколько цифр или не имели механизма переноса между цифрами аккумулятор.

Счетные машины не стали коммерчески выгодными до 1851 г., когда Томас де Кольмар выпустил после тридцати лет разработки свой упрощенный арифмометр, первая машина, достаточно мощная для ежедневного использования в офисе. Арифмометр был разработан вокруг Колеса Лейбница и первоначально использовал Паскаля Дополнение 9 метод вычитания.

Смотрите также

• Счетная машина
• Ступенчатый счетчик
• Арифмометр
• Комптометр
• Различный двигатель
• Аналитическая машина
• Z1 (компьютер)

Примечания

1. Uvres de Pascal в 5 томах, La Haye, 1779
2. Журнал Nature, (1942)
3. Фальк, Джим (14 ноября 2014 г.). "Паскалин Блеза Паскаля". Вещи, которые считаются. Получено 31 января, 2016.
4. (фр) La Machine d’arithmétique, Блез Паскаль, Wikisource
5. Гай Мурлеват, п. 12 (1988)
6. Лиланд Лок, п. 316 (1933)
7. Празднование трехсотлетия Паскаля, Лондон (1942 г.). Журнал Nature, (1942)
8. Гай Мурлеват, п. 29 (1988). "Toutes les machines arithmétiques inventory .... sauf la machine tardive du C.N.A.M .... ont deux rayons contigus marqués".
9. Гай Мурлеват, п. 29 (1988). «... пальметта, мелкие кусочки, грифоны, вернис».
10. Использование машины, Courrier du center international Blaise Pascal, Клермон-Ферран, № 8, 1986
11. Гай Мурлеват, стр. 31–33 (1988).
12. Гай Мурлеват, п. 27 (1988)
13. Avis nécessaire à ceux qui auront curiosité de voir la Machine d'Arithmétique et de s'en servir Wikisource: La Machine d’arithmétique, Blaise Pascal
14. Жан Маргин, п. 41 (1994)
15. Гай Мурлеват, п.17 (1988)
16. Курьер дю CIBP, № 8, стр. 9, (1986)
17. Гай Мурлеват, п. 30 (1988)
18. Гай Мурлеват, п. 38 (1988)
19. «Архивная копия». Архивировано из оригинал на 2011-10-15. Получено 2011-11-19.
20. Гай Мурлеват, Генеалогия, (1988)
21. «Архивная копия». Архивировано из оригинал на 2011-10-19. Получено 2011-11-05.
22. http://www-03.ibm.com/ibm/history/exhibits/attic3/attic3_room3.html
23. Жан Маргин, п. 46 (1994)
24. (fr) Wikisource: Privilège du Roi, pour la Machine Arithmétique La Machine d’arithmétique, Блез Паскаль
25. Энциклопедия Дидро и Даламбера, Том I, 1-е издание, стр. 680-681
26. Wikisource: Avis nécessaire à ceux qui auront curiosité de voir la Machine d'Arithmétique et de s'en servir La Machine d’arithmétique, Блез Паскаль
27. Стэн Аугартен, п. 20, (1984)
28. Жан Маргин, стр. 46-48 (1994).
29. Счетные часы Вильгельма Шикарда. Проверено 31 января 2012 г.
30. Майкл Уильямс, п. 122 (1997)
31. Майкл Уильямс, стр. 124, 128 (1997).
32. Эрик Сведин, п. 11 (2005)
33. Жан Маргин, стр. 64–65 (1994).
34. Scripta Mathematica, п. 149 (1932)
35. Жан Маргин, п. 66
36. Клод Перро, п. 38 (1700).

Источники

• Видаль, Натали; Фогт, Доминик (2011). Les Machines Arithmétiques de Blaise Pascal (На французском). Клермон-Ферран: Muséum Henri-Lecoq. ISBN  978-2-9528068-4-8.
• Паскаль, Блез (1779). Oeuvres de Blaise Pascal (На французском). La Haye: Chez Detune.
• Элленбергер, Мишель; Коллин, Мари – Марта (1993). La machine à calculer de Blaise Pascal (На французском). Пэрис: Натан.
• Мурлеват, Гай (1988). Арифметические машины Блеза Паскаля (На французском). Клермон-Ферран: La Française d'Edition et d'Imprimerie.
• Маргин, Жан (1994). История инструментов и машин для калькулятора, Trois siècles de mécanique pensante 1642–1942 (На французском). Германн. ISBN  978-2-7056-6166-3.
• Татон, Рене (1949). Le Calcul mécanique. Que sais-je? № 367 (На французском). Университеты Франции.
• Татон, Рене (1963). Le Calcul mécanique. Que sais-je? № 367 (На французском). Университеты Франции. С. 20–28.
• Татон, Рене (1969). Histoire du Calcul. Que sais-je? № 198 (На французском). Университеты Франции.
• Коллектив (1942). Каталог музеев - Раздел A Инструменты и аппараты на счетчике (На французском). Париж: Национальная консерватория искусств и ремесел.
• Гинзбург, Джекитиэль (2003). Scripta Mathematica (сентябрь 1932 г. - июнь 1933 г.). Кессинджер Паблишинг, ООО. ISBN  978-0-7661-3835-3.
• Нидхэм, Джозеф (1986). Наука и цивилизация в Китае: Том 4, Физика и физические технологии, Часть 2, Машиностроение. Тайбэй: Caves Books, Ltd.
• Ифра, Жорж (2000). Всеобщая история чисел. John Wiley & Sons, Inc. ISBN  0-471-39671-0.
• Ифра, Жорж (2001). Универсальная история вычислительной техники. John Wiley & Sons, Inc. ISBN  0-471-39671-0.
• Войлок, Дорр Э. (1916). Механическая арифметика, или История счетной машины. Чикаго: Вашингтонский институт.
• д'Окань, Морис (1893). Annales du Conservatoire national des arts et métier, 2e série, tome 5, Le Calculальном упрощифи (На французском). Париж: Gauthiers-Villars et files, Imprimeurs-Libraires.
• Уильямс, Майкл Р. (1997). История вычислительной техники. Лос-Аламитос, Калифорния: Компьютерное общество IEEE. ISBN  0-8186-7739-2.
• Епископ, Моррис (1936). Паскаль, Жизнь гения. Нью-Йорк: Рейнал и Хичкок.
• Сведин, Эрик Г.; Ферро, Дэвид Л. (2005). Компьютеры: история жизни технологии. Вестпорт, Коннектикут: Гринвуд. ISBN  0-8018-8774-7.
• Перро, Клод (1700). Recueil de plusieurs Machines de Nouvelle Изобретение. Париж, Франция: Жан Батист Куаньяр.
• М.Е.П. (31 октября 1942 г.). "Празднование 300-летия Паскаля". Природа. Лондон. 150 (3809): 527. Дои:10.1038 / 150527a0.
• Проф. С. Чепмен (31 октября 1942 г.). "Блез Паскаль (1623–1662) 300-летие счетной машины". Природа. Лондон. 150: 508–509. Дои:10.1038 / 150508a0.
• «Использование машины». Courrier du Centre International Blaise Pascal (На французском). Клермон-Ферран (8): 4–25. 1986 г.

внешняя ссылка

• Веб-сайт, объясняющий работу Паскалина.
• Подробная анимация, объясняющая, как работает Паскалин.
• Более подробно об истории Pascaline и современных реплик.
• Подробнее об «инструкции по эксплуатации» для Pascaline.
• "Avis nécessaire à ceux qui auront curiosité de voir ladite Machine et s'en servir" (Паскалин, 1635 г.), онлайн-текст и анализ на BibNum [щелкните "à télécharger" для английской версии].