Нелинейное уменьшение размерности - Nonlinear dimensionality reduction

Многомерный данные, то есть данные, для представления которых требуется более двух или трех измерений, могут быть трудно интерпретировать. Один из подходов к упрощению - предположить, что интересующие данные лежат на встроенный нелинейный многообразие в пределах многомерное пространство. Если коллектор имеет достаточно низкую размерность, данные могут быть визуализированы в низкоразмерном пространстве.

Вверху слева: набор 3D-данных из 1000 точек в спиралевидной полосе (также известный как рулет с вареньем ) с прямоугольным отверстием посередине. Вверху справа: исходный 2D-коллектор, используемый для создания набора 3D-данных. Внизу слева и справа: 2D-восстановления многообразия соответственно с использованием LLE и Гессен LLE алгоритмы, реализованные с помощью инструментария модульной обработки данных.

Ниже приводится краткое изложение некоторых важных алгоритмов из истории многообразное обучение и уменьшение нелинейной размерности (NLDR).^[1][2] Многие из этих нелинейных уменьшение размерности методы относятся к линейные методы, перечисленные ниже. Нелинейные методы можно в общих чертах разделить на две группы: те, которые обеспечивают отображение (из многомерного пространства в низкоразмерное встраивание, или наоборот), и те, которые просто дают визуализацию. В контексте машинное обучение, методы картирования можно рассматривать как предварительные извлечение признаков шаг, после которого алгоритмы распознавания образов применяются. Обычно те, которые просто визуализируют, основаны на данных близости, то есть расстояние измерения.

Связанные методы линейного разложения

• Независимый компонентный анализ (МКА).
• Анализ главных компонентов (PCA) (также называемый Теорема Карунена – Лоэва - КЛТ).
• Разложение по сингулярным числам (СВД).
• Факторный анализ.

Применение NLDR

Рассмотрим набор данных, представленный в виде матрицы (или таблицы базы данных), так что каждая строка представляет набор атрибутов (или функций или размеров), которые описывают конкретный экземпляр чего-либо. Если количество атрибутов велико, то пространство уникальных возможных строк экспоненциально велико. Таким образом, чем больше размерность, тем сложнее становится отсчет пространства. Это вызывает множество проблем. Алгоритмы, работающие с многомерными данными, обычно имеют очень высокую временную сложность. Например, многие алгоритмы машинного обучения борются с многомерными данными. Это стало известно как проклятие размерности. Сокращение данных до меньшего числа измерений часто делает алгоритмы анализа более эффективными и может помочь алгоритмам машинного обучения делать более точные прогнозы.

Люди часто испытывают трудности с пониманием данных во многих измерениях. Таким образом, сокращение данных до небольшого количества измерений полезно для целей визуализации.

График двумерных точек, полученных в результате использования алгоритма NLDR. В этом случае Manifold Sculpting используется для сокращения данных до двух измерений (вращения и масштабирования).

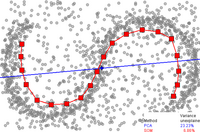
Представления данных с уменьшенной размерностью часто называют «внутренними переменными». Это описание подразумевает, что это значения, из которых были получены данные. Например, рассмотрим набор данных, содержащий изображения буквы «А», которая была масштабирована и повернута на разные величины. Каждое изображение имеет размер 32x32 пикселя. Каждое изображение может быть представлено как вектор из 1024 значений пикселей. Каждая строка является образцом на двумерном многообразии в 1024-мерном пространстве ( Пространство Хэмминга ). Внутренняя размерность равна двум, потому что две переменные (поворот и масштаб) менялись для получения данных. Информация о форме или внешнем виде буквы «А» не является частью внутренних переменных, потому что она одинакова во всех случаях. Нелинейное уменьшение размерности отбросит коррелированную информацию (буква «А») и восстановит только изменяющуюся информацию (поворот и масштаб). На изображении справа показаны образцы изображений из этого набора данных (для экономии места показаны не все входные изображения) и график двухмерных точек, полученных в результате использования алгоритма NLDR (в этом случае использовалось скульптурное моделирование манифольда) чтобы сократить данные до двух измерений.

PCA (алгоритм уменьшения линейной размерности) используется для сокращения этого же набора данных до двух измерений, итоговые значения не так хорошо организованы.

Для сравнения, если Анализ главных компонентов, который представляет собой алгоритм уменьшения линейной размерности, используется для сокращения этого же набора данных до двух измерений, итоговые значения не так хорошо организованы. Это демонстрирует, что многомерные векторы (каждый из которых представляет букву «А»), образующие это многообразие, изменяются нелинейным образом.

Таким образом, должно быть очевидно, что NLDR имеет несколько приложений в области компьютерного зрения. Например, рассмотрим робота, который использует камеру для навигации в замкнутой статической среде. Изображения, полученные с помощью этой камеры, можно рассматривать как образцы на многообразии в многомерном пространстве, и внутренние переменные этого многообразия будут представлять положение и ориентацию робота. Эта утилита не ограничивается роботами. Динамические системы, более общий класс систем, в который входят роботы, определяются в терминах многообразия. Активные исследования в области NLDR направлены на раскрытие многообразия наблюдений, связанных с динамическими системами, для разработки методов моделирования таких систем и обеспечения их автономной работы.^[3]

Некоторые из наиболее известных разнообразных алгоритмов обучения перечислены ниже. Алгоритм может изучить внутренняя модель данных, которые могут быть использованы для отображения точек, недоступных во время обучения, во встраивание в процесс, который часто называют расширением вне выборки.

Важные концепции

Карта Саммона

Карта Саммона является одним из первых и самых популярных методов NLDR.

Аппроксимация главной кривой одномерным SOM (а пунктирная линия с красными квадратами, 20 узлов). Первый главный компонент представлен синей прямой линией. Точки данных - это маленькие серые кружки. Для PCA Необъяснимая доля дисперсии в этом примере - 23,23%, для SOM - 6,86%.^[4]

Самоорганизующаяся карта

В самоорганизующаяся карта (SOM, также называемый Карта Кохонена) и его вероятностный вариант генеративное топографическое картирование (GTM) использовать точечное представление во встроенном пространстве для формирования скрытая переменная модель основанный на нелинейном отображении вложенного пространства в многомерное пространство.^[5] Эти техники связаны с работой над сети плотности, которые также основаны на той же вероятностной модели.

Анализ основных компонентов ядра

Возможно, наиболее широко используемый алгоритм для обучения многообразию - это ядро PCA.^[6] Это комбинация Анализ главных компонентов и трюк с ядром. PCA начинается с вычисления ковариационной матрицы ${\displaystyle m\times n}$ матрица ${\displaystyle \mathbf {X} }$

${\displaystyle C={\frac {1}{m}}\sum _{i=1}^{m}{\mathbf {x} _{i}\mathbf {x} _{i}^{\mathsf {T}}}.}$

Затем он проецирует данные на первый k собственные векторы этой матрицы. Для сравнения, KPCA начинается с вычисления ковариационной матрицы данных после преобразования в многомерное пространство,

${\displaystyle C={\frac {1}{m}}\sum _{i=1}^{m}{\Phi (\mathbf {x} _{i})\Phi (\mathbf {x} _{i})^{\mathsf {T}}}.}$

Затем он проецирует преобразованные данные на первый k собственные векторы этой матрицы, как и PCA. Он использует трюк с ядром, чтобы убрать большую часть вычислений, так что весь процесс может быть выполнен без фактических вычислений. ${\displaystyle \Phi (\mathbf {x} )}$. Конечно ${\displaystyle \Phi }$ должен быть выбран так, чтобы ему было известно соответствующее ядро. К сожалению, найти хорошее ядро ​​для данной проблемы нетривиально, поэтому KPCA не дает хороших результатов с некоторыми проблемами при использовании стандартных ядер. Например, известно, что эти ядра плохо работают на рулет с вареньем многообразие. Однако можно рассматривать некоторые другие методы, которые хорошо работают в таких условиях (например, собственные лапласовские карты, LLE), как частные случаи ядра PCA, создавая зависимую от данных матрицу ядра.^[7]

KPCA имеет внутреннюю модель, поэтому ее можно использовать для сопоставления точек на ее встраивании, которые не были доступны во время обучения.

Основные кривые и многообразия

Применение основных кривых: Нелинейный индекс качества жизни.^[8] Точки представляют данные ООН 171 страна в 4-х мерном пространстве, образованном значениями 4 показателей: валовой продукт на душу населения, продолжительность жизни, младенческая смертность, туберкулез заболеваемость. Разные формы и цвета соответствуют разным географическим местам. Красная жирная линия представляет главная кривая, аппроксимируя набор данных. Эта основная кривая была построена методом эластичная карта. Программное обеспечение доступно для бесплатного некоммерческого использования.^[9][10]

Основные кривые и коллекторы дают естественную геометрическую основу для нелинейного уменьшения размерности и расширяют геометрическую интерпретацию PCA путем явного построения вложенного многообразия и кодирования с использованием стандартной геометрической проекции на многообразие. Такой подход был предложен Тревор Хасти в своей диссертации (1984)^[11] и разработан многими авторами.^[12]Как определить "простоту" многообразия зависит от проблемы, однако обычно она измеряется внутренней размерностью и / или гладкостью многообразия. Обычно главное многообразие определяется как решение задачи оптимизации. Целевая функция включает в себя качество аппроксимации данных и некоторые штрафные члены за изгиб многообразия. Популярные начальные приближения генерируются линейным PCA, SOM Кохонена или автоэнкодерами. В эластичная карта метод обеспечивает алгоритм максимизации ожидания для главного многообразное обучение с минимизацией квадратичного функционала энергии на шаге «максимизации».

Собственные карты лапласиана

Смотрите также: Регуляризация многообразия

Лапласовские собственные карты используют спектральные методы для уменьшения размерности.^[13] Этот метод основан на основном предположении, что данные лежат в низкоразмерном многообразии в многомерном пространстве.^[14] Этот алгоритм не может включать точки вне выборки, но методы, основанные на Воспроизведение ядра гильбертова пространства существует регуляризация для добавления этой возможности.^[15] Такие методы могут быть применены и к другим алгоритмам нелинейного уменьшения размерности.

Традиционные методы, такие как анализ главных компонентов, не учитывают внутреннюю геометрию данных. Собственные карты Лапласа строят граф на основе информации о соседстве набора данных. Каждая точка данных служит узлом на графике, а связь между узлами регулируется близостью соседних точек (например, с помощью алгоритм k-ближайшего соседа ). Созданный таким образом граф можно рассматривать как дискретное приближение низкоразмерного многообразия в многомерном пространстве. Минимизация функции стоимости на основе графика гарантирует, что точки, близкие друг к другу на многообразии, отображаются близко друг к другу в низкоразмерном пространстве с сохранением локальных расстояний. Собственные функции Оператор Лапласа – Бельтрами на многообразии служат размерностями вложения, поскольку при мягких условиях этот оператор имеет счетный спектр, который является базисом для квадратично интегрируемых функций на многообразии (ср. Ряд Фурье на многообразии единичной окружности). Попытки разместить собственные карты Лапласа на твердой теоретической основе увенчались некоторым успехом, поскольку при определенных неограничивающих предположениях матрица лапласа графа сходится к оператору Лапласа – Бельтрами, когда число точек стремится к бесконечности.^[14]

В приложениях классификации низкоразмерные коллекторы могут использоваться для моделирования классов данных, которые могут быть определены из наборов наблюдаемых экземпляров. Каждый наблюдаемый экземпляр может быть описан двумя независимыми факторами, называемыми 'контент' и 'стиль', где 'контент' является инвариантным фактором, связанным с сущностью класса, а 'стиль' выражает вариации в этом классе между экземплярами.^[16] К сожалению, лапласовские собственные карты могут не дать связного представления интересующего класса, если обучающие данные состоят из экземпляров, значительно различающихся по стилю.^[17] В случае классов, которые представлены многомерными последовательностями, были предложены структурные лапласианские собственные карты для преодоления этой проблемы путем добавления дополнительных ограничений в граф информации о соседстве лапласовских собственных карт, чтобы лучше отражать внутреннюю структуру класса.^[18] Более конкретно, граф используется для кодирования как последовательной структуры многомерных последовательностей, так и, для минимизации стилистических вариаций, близости между точками данных различных последовательностей или даже внутри последовательности, если она содержит повторы. С помощью динамическое искажение времени, близость обнаруживается путем нахождения соответствий между и внутри участков многомерных последовательностей, которые демонстрируют высокое сходство. Эксперименты проводились на распознавание активности на основе зрения, приложения для классификации ориентации объектов и восстановления трехмерных поз человека продемонстрировали дополнительную ценность структурных лапласовских собственных карт при работе с многомерными данными последовательности.^[18] Расширение структурных лапласовских собственных карт, обобщенных лапласовских собственных карт привело к созданию многообразий, в которых одно из измерений конкретно представляет вариации стиля. Это оказалось особенно полезным в таких приложениях, как отслеживание шарнирного тела человека и извлечение силуэта.^[19]

Isomap

Isomap^[20] представляет собой комбинацию Алгоритм Флойда-Уоршолла с классикой Многомерное масштабирование. Классическое многомерное масштабирование (MDS) берет матрицу попарных расстояний между всеми точками и вычисляет положение для каждой точки. Isomap предполагает, что попарные расстояния известны только между соседними точками, и использует алгоритм Флойда – Уоршалла для вычисления попарных расстояний между всеми другими точками. Это эффективно оценивает полную матрицу попарных геодезические расстояния между всеми точками. Затем Isomap использует классическую MDS для вычисления положений всех точек в уменьшенном масштабе. Landmark-Isomap - вариант этого алгоритма, который использует ориентиры для увеличения скорости за счет некоторой точности.

При многократном обучении предполагается, что входные данные берутся из низкоразмерного многообразие который встроен в многомерное векторное пространство. Основная идея MVU - использовать локальную линейность многообразий и создать отображение, сохраняющее локальные окрестности в каждой точке лежащего в основе многообразия.

Локально-линейное вложение

Локально-линейное вложение (LLE)^[21] был представлен примерно в то же время, что и Isomap. Он имеет несколько преимуществ перед Isomap, в том числе более быструю оптимизацию при реализации разреженная матрица алгоритмы и лучшие результаты со многими проблемами. LLE также начинается с нахождения набора ближайших соседей каждой точки. Затем он вычисляет набор весов для каждой точки, который лучше всего описывает точку как линейную комбинацию ее соседей. Наконец, он использует метод оптимизации на основе собственных векторов, чтобы найти низкоразмерное вложение точек, так что каждая точка по-прежнему описывается той же линейной комбинацией своих соседей. LLE имеет тенденцию плохо справляться с неоднородной плотностью образцов, потому что не существует фиксированной единицы измерения, предотвращающей смещение весов, поскольку различные области различаются по плотности образца. LLE не имеет внутренней модели.

LLE вычисляет барицентрические координаты точки Икс_я на основе своих соседей Икс_j. Исходная точка восстанавливается линейной комбинацией, заданной весовой матрицей W_ij, своих соседей. Ошибка реконструкции определяется функцией стоимости E(W).

${\displaystyle E(W)=\sum _{i}|{\mathbf {X} _{i}-\sum _{j}{\mathbf {W} _{ij}\mathbf {X} _{j}}|}^{\mathsf {2}}}$

Веса W_ij относится к сумме взноса балл Икс_j имеет при восстановлении точки Икс_я. Функция стоимости минимизируется при двух ограничениях: (a) Каждая точка данных Икс_я реконструируется только по соседям, таким образом W_ij быть нулем, если точка Икс_j не сосед по делу Икс_я и (b) сумма каждой строки весовой матрицы равна 1.

${\displaystyle \sum _{j}{\mathbf {W} _{ij}}=1}$

Исходные точки данных собираются в D размерное пространство, и цель алгоритма - уменьшить размерность до d такой, что D >> d. Одинаковые веса W_ij который реконструирует я-я точка данных в D пространство измерений будет использоваться для восстановления той же точки в нижнем d пространственное пространство. На основе этой идеи создается карта сохранения окрестностей. Каждая точка X_я в D мерное пространство отображается на точку Y_я в d размерное пространство за счет минимизации функции стоимости

${\displaystyle C(Y)=\sum _{i}|{\mathbf {Y} _{i}-\sum _{j}{\mathbf {W} _{ij}\mathbf {Y} _{j}}|}^{\mathsf {2}}}$

В этой функции стоимости, в отличие от предыдущей, веса W_ij фиксируются, и минимизация выполняется в точках Y_я для оптимизации координат. Эта проблема минимизации может быть решена путем решения разреженного N Икс N проблема собственных значений (N количество точек данных), нижняя часть которой d ненулевые собственные векторы обеспечивают ортогональный набор координат. Обычно точки данных реконструируются из K ближайших соседей, измеренных Евклидово расстояние. Для такой реализации в алгоритме есть только один свободный параметр K, который можно выбрать путем перекрестной проверки.

Гессенское локально-линейное вложение (Hessian LLE)

Как LLE, Гессен LLE также основан на методах разреженных матриц.^[22] Он имеет тенденцию давать результаты гораздо более высокого качества, чем LLE. К сожалению, он имеет очень дорогостоящую вычислительную сложность, поэтому он не очень хорошо подходит для сильно дискретизированных многообразий. У него нет внутренней модели.

Модифицированное локально-линейное вложение (MLLE)

Модифицированный LLE (MLLE)^[23] это еще один вариант LLE, который использует несколько весов в каждой окрестности для решения проблемы согласования локальной весовой матрицы, которая приводит к искажениям в картах LLE. Грубо говоря, множественные веса - это локальные ортогональная проекция оригинальных гирь производства LLE. Создатели этого регуляризованного варианта также являются авторами Local Tangent Space Alignment (LTSA), которое подразумевается в формулировке MLLE, когда понимается, что глобальная оптимизация ортогональных проекций каждого весового вектора, по сути, выравнивает локальные касательные пространства. каждой точки данных. Теоретические и эмпирические выводы от правильного применения этого алгоритма имеют далеко идущие последствия.^[24]

Выравнивание местного касательного пространства

Основная статья: Выравнивание местного касательного пространства

LTSA^[25] основан на интуиции, что при правильном развертывании коллектора все касательные гиперплоскости к нему выровняются. Он начинается с вычисления k-ближайшие соседи каждой точки. Он вычисляет касательное пространство в каждой точке, вычисляя d-первые главные компоненты в каждой локальной окрестности. Затем он оптимизируется, чтобы найти вложение, выравнивающее касательные пространства.

Максимальное раскрытие дисперсии

Максимальное раскрытие дисперсии, Изокарта и локально линейное вложение разделяют общую интуицию, основанную на представлении о том, что если многообразие правильно развернуто, то дисперсия по точкам максимальна. Его начальный шаг, такой как Isomap и Local Linear Embedding, - это поиск k-ближайшие соседи каждой точки. Затем он пытается решить проблему максимального увеличения расстояния между всеми несоседними точками, ограниченного таким образом, чтобы расстояния между соседними точками сохранялись. Основным вкладом этого алгоритма является метод преобразования этой проблемы в задачу полуопределенного программирования. К сожалению, решатели с полуопределенным программированием требуют больших вычислительных затрат. Как и локально линейное вложение, у него нет внутренней модели.

Автоэнкодеры

An автоэнкодер это прямая связь нейронная сеть который обучен приближать функцию идентичности. То есть он обучен отображать из вектора значений в тот же вектор. При использовании в целях уменьшения размерности один из скрытых слоев в сети ограничен, чтобы содержать только небольшое количество сетевых блоков. Таким образом, сеть должна научиться кодировать вектор в небольшое количество измерений, а затем декодировать его обратно в исходное пространство. Таким образом, первая половина сети представляет собой модель, которая отображает пространство высокой размерности в пространство низкой размерности, а вторая половина карты отображает пространство низкой размерности в пространство высокой размерности. Хотя идея автоэнкодеров довольно старая, обучение глубоких автоэнкодеров стало возможным только недавно благодаря использованию ограниченные машины Больцмана и составные автокодеры шумоподавления. К автоэнкодерам относится NeuroScale алгоритм, который использует функции напряжения, вдохновленные многомерное масштабирование и Отображения Саммона (см. выше), чтобы изучить нелинейное отображение многомерного пространства во вложенное. Отображения в NeuroScale основаны на сети с радиальными базисными функциями. Другое использование нейронной сети для уменьшения размерности - научить ее изучать касательные плоскости в данных.^[26]

Гауссовские модели скрытых переменных процессов

Гауссовские модели скрытых переменных процессов (GPLVM)^[27] представляют собой вероятностные методы уменьшения размерности, в которых используются гауссовские процессы (GP) для поиска нелинейного вложения более низкой размерности для данных большой размерности. Они являются расширением вероятностной формулировки PCA. Модель определяется вероятностным образом, затем скрытые переменные маргинализируются, а параметры получаются путем максимизации вероятности. Как и ядро ​​PCA, они используют функцию ядра для формирования нелинейного отображения (в форме Гауссовский процесс ). Однако в GPLVM отображение происходит из встроенного (скрытого) пространства в пространство данных (например, сети плотности и GTM), тогда как в ядре PCA это происходит в противоположном направлении. Первоначально он был предложен для визуализации данных большой размерности, но был расширен для построения общей модели многообразия между двумя пространствами наблюдения. GPLVM и многие ее варианты были предложены специально для моделирования движения человека, например, GPLVM с задними ограничениями, динамическая модель GP (GPDM ), сбалансированный GPDM (B-GPDM) и GPDM с топологическими ограничениями. Чтобы уловить эффект связи многообразия позы и походки в анализе походки, было предложено многослойное объединенное многообразие позы и походки.^[28]

t-распределенное стохастическое вложение соседей

t-распределенное стохастическое вложение соседей (t-SNE)^[29] широко используется. Это один из семейства методов стохастического вложения соседей. Алгоритм вычисляет вероятность того, что пары точек данных в многомерном пространстве связаны, а затем выбирает низкоразмерные вложения, которые производят подобное распределение.

Другие алгоритмы

Карта реляционной перспективы

Карта реляционной перспективы - это многомерное масштабирование алгоритм. Алгоритм находит конфигурацию точек данных на многообразии путем моделирования многочастичной динамической системы на замкнутом многообразии, где точки данных отображаются на частицы, а расстояния (или несходство) между точками данных представляют собой силу отталкивания. По мере постепенного увеличения размера коллектора система из множества частиц постепенно остывает и сходится к конфигурации, которая отражает информацию о расстоянии точек данных.

Карта реляционной перспективы была вдохновлена ​​физической моделью, в которой положительно заряженные частицы свободно перемещаются по поверхности шара. Руководствуясь Кулон сила между частицами минимальная энергетическая конфигурация частиц будет отражать силу сил отталкивания между частицами.

Карта реляционной перспективы была представлена ​​в.^[30]Алгоритм впервые использовал плоский тор как коллектор изображений, то он был расширен (в ПО VisuMap использовать другие типы закрытых коллекторов, например сфера, проективное пространство, и Бутылка Клейна, как многообразия изображений.

Карты заражения

Карты заражения используют несколько заражений в сети для отображения узлов в виде облака точек.^[31] В случае Модель глобальных каскадов скорость распространения можно регулировать с помощью порогового параметра ${\displaystyle t\in [0,1]}$. За ${\displaystyle t=0}$ карта заражения эквивалентна Isomap алгоритм.

Анализ криволинейных компонентов

Анализ криволинейных компонентов (CCA) ищет конфигурацию точек в выходном пространстве, которая сохраняет исходные расстояния в максимально возможной степени, фокусируясь на малых расстояниях в выходном пространстве (наоборот, Карта Саммона которые фокусируются на небольших расстояниях в исходном пространстве).^[32]

Следует отметить, что CCA, как алгоритм итеративного обучения, фактически начинается с фокусировки на больших расстояниях (например, алгоритм Сэммона), а затем постепенно меняет фокус на небольшие расстояния. Информация о малом расстоянии перезапишет информацию о большом расстоянии, если между ними придется пойти на компромисс.

Функция напряжения ОСА связана с суммой правых дивергенций Брегмана.^[33]

Анализ криволинейных расстояний

CDA^[32] тренирует самоорганизующуюся нейронную сеть, чтобы она соответствовала многообразию, и стремится сохранить геодезические расстояния в его встраивании. Он основан на анализе криволинейных компонентов (который расширил отображение Сэммона), но вместо этого использует геодезические расстояния.

Диффеоморфное снижение размерности

Диффеоморфный Уменьшение размерности или Диффеокарта^[34] изучает гладкое диффеоморфное отображение, которое переносит данные в линейное подпространство меньшей размерности. Эти методы решают для гладкого индексированного по времени векторного поля, так что потоки вдоль поля, которые начинаются в точках данных, заканчиваются в линейном подпространстве меньшей размерности, тем самым пытаясь сохранить попарные различия как при прямом, так и при обратном отображении.

Выравнивание коллектора

Выравнивание коллектора использует в своих интересах предположение, что разрозненные наборы данных, созданные аналогичными процессами генерации, будут иметь аналогичное базовое многообразное представление. Изучая проекции из каждого исходного пространства в общее многообразие, восстанавливаются соответствия, и знания из одной области могут быть перенесены в другую. Большинство методик множественного выравнивания рассматривают только два набора данных, но эта концепция распространяется на произвольно множество исходных наборов данных.^[35]

Карты диффузии

Карты диффузии использует взаимосвязь между теплом распространение и случайная прогулка (Цепь Маркова ); проводится аналогия между оператором диффузии на многообразии и марковской переходной матрицей, оперирующей функциями, определенными на графе, узлы которого были взяты из многообразия.^[36] В частности, пусть набор данных представлен как ${\displaystyle \mathbf {X} =[x_{1},x_{2},\ldots ,x_{n}]\in \Omega \subset \mathbf {R^{D}} }$. Основное предположение карты диффузии состоит в том, что многомерные данные лежат на низкоразмерном многообразии размерности. ${\displaystyle \mathbf {d} }$. Позволять Икс представляют набор данных и ${\displaystyle \mu }$ представляют собой распределение точек данных на Икс. Далее, определим ядро что представляет собой некоторое понятие сродства точек в Икс. Ядро ${\displaystyle {\mathit {k}}}$ имеет следующие свойства^[37]

${\displaystyle k(x,y)=k(y,x),\,}$

k симметричен

${\displaystyle k(x,y)\geq 0\qquad \forall x,y,k}$

k сохраняет позитив

Таким образом, можно думать об отдельных точках данных как об узлах графа и ядра. k как определение некоторого родства на этом графе. Граф симметричен по построению, так как ядро ​​симметрично. Здесь легко увидеть, что из кортежа (Икс,k) можно построить обратимый Цепь Маркова. Этот метод является общим для множества полей и известен как лапласиан графа.

Например, график K = (Икс,E) можно построить с помощью гауссова ядра.

${\displaystyle K_{ij}={\begin{cases}e^{-\|x_{i}-x_{j}\|_{2}^{2}/\sigma ^{2}}&{\text{if }}x_{i}\sim x_{j}\\0&{\text{otherwise}}\end{cases}}}$

В приведенном выше уравнении ${\displaystyle x_{i}\sim x_{j}}$ означает, что ${\displaystyle x_{i}}$ ближайший сосед ${\displaystyle x_{j}}$. Правильно, Геодезический расстояние следует использовать для фактического измерения расстояний на многообразие. Поскольку точная структура многообразия недоступна, для ближайших соседей геодезическое расстояние аппроксимируется евклидовым расстоянием. Выбор ${\displaystyle \sigma }$ модулирует наше понятие близости в том смысле, что если ${\displaystyle \|x_{i}-x_{j}\|_{2}\gg \sigma }$ тогда ${\displaystyle K_{ij}=0}$ и если ${\displaystyle \|x_{i}-x_{j}\|_{2}\ll \sigma }$ тогда ${\displaystyle K_{ij}=1}$. Первое означает, что произошла очень небольшая диффузия, а второе подразумевает, что процесс диффузии почти завершен. Различные стратегии на выбор ${\displaystyle \sigma }$ можно найти в.^[38]

Чтобы точно представить матрицу Маркова, ${\displaystyle K}$ должны быть нормированы соответствующими матрица степеней ${\displaystyle D}$:

${\displaystyle P=D^{-1}K.\,}$

${\displaystyle P}$ теперь представляет собой цепь Маркова. ${\displaystyle P(x_{i},x_{j})}$ вероятность перехода от ${\displaystyle x_{i}}$ к ${\displaystyle x_{j}}$ за один временной шаг. Аналогично вероятность перехода от ${\displaystyle x_{i}}$ к ${\displaystyle x_{j}}$ в т временные шаги задаются ${\displaystyle P^{t}(x_{i},x_{j})}$. Здесь ${\displaystyle P^{t}}$ матрица ${\displaystyle P}$ умноженный на себя т раз.

Матрица Маркова ${\displaystyle P}$ составляет некоторое представление о локальной геометрии набора данных Икс. Основное различие между диффузионными картами и Анализ главных компонентов заключается в том, что на диффузионных картах учитываются только локальные особенности данных, а не корреляция всего набора данных.

${\displaystyle K}$ определяет случайное блуждание по набору данных, что означает, что ядро ​​фиксирует некоторую локальную геометрию набора данных. Цепь Маркова определяет быстрое и медленное направления распространения значений ядра. По мере того, как блуждание распространяется вперед во времени, информация о локальной геометрии накапливается так же, как и локальные переходы (определяемые дифференциальными уравнениями) динамической системы.^[37] Метафора диффузии возникает из определения расстояния распространения в семье {${\displaystyle D_{t}}$}${\displaystyle _{t\in N}}$

${\displaystyle D_{t}^{2}(x,y)=||p_{t}(x,\cdot )-p_{t}(y,\cdot )||^{2}}$

При фиксированном t ${\displaystyle D_{t}}$ определяет расстояние между любыми двумя точками набора данных на основе связности пути: значение ${\displaystyle D_{t}(x,y)}$ будет тем меньше, чем больше путей соединяет Икс к у наоборот. Потому что количество ${\displaystyle D_{t}(x,y)}$ включает в себя сумму всех путей длины t, ${\displaystyle D_{t}}$ гораздо более устойчив к шуму в данных, чем геодезическое расстояние. ${\displaystyle D_{t}}$ учитывает все отношения между точками x и y при вычислении расстояния и служит лучшим понятием близости, чем просто Евклидово расстояние или даже геодезическое расстояние.

Локальное многомерное масштабирование

Локальное многомерное масштабирование выполняет многомерное масштабирование в локальных регионах, а затем использует выпуклую оптимизацию, чтобы собрать все части вместе.^[39]

Нелинейный PCA

Нелинейный PCA (NLPCA) использует обратное распространение обучить многослойный персептрон (MLP) подходить к коллектору.^[40] В отличие от типичного обучения MLP, при котором обновляются только веса, NLPCA обновляет и веса, и входные данные. То есть и веса, и входные данные рассматриваются как скрытые значения. После обучения латентные входные данные представляют собой низкоразмерное представление наблюдаемых векторов, а MLP отображает это низкоразмерное представление в многомерное пространство наблюдения.

Крупномасштабное масштабирование на основе данных

Высокомерное масштабирование на основе данных (DD-HDS)^[41] тесно связан с Карта Саммона и криволинейный компонентный анализ, за ​​исключением того, что (1) он одновременно штрафует ложные окрестности и разрывы, фокусируясь на малых расстояниях как в исходном, так и в выходном пространстве, и что (2) он учитывает концентрация меры явление, адаптировав весовую функцию к распределению расстояний.

Скульптура манифольдов

Моделирование манифольдов^[42] использует постепенная оптимизация найти вложение. Как и другие алгоритмы, он вычисляет k-ближайшие соседи и пытается найти вложение, которое сохраняет отношения в местных окрестностях. Он медленно масштабирует дисперсию из более высоких измерений, одновременно корректируя точки в более низких измерениях, чтобы сохранить эти отношения. Если скорость масштабирования мала, можно найти очень точные вложения. Он может похвастаться более высокой эмпирической точностью, чем другие алгоритмы с несколькими проблемами. Его также можно использовать для уточнения результатов других разнообразных алгоритмов обучения. Однако он изо всех сил пытается развернуть некоторые коллекторы, если не используется очень низкая скорость масштабирования. У него нет модели.

RankVisu

RankVisu^[43] предназначен для сохранения ранга соседства, а не расстояния. RankVisu особенно полезен в сложных задачах (когда невозможно добиться удовлетворительного сохранения расстояния). Действительно, ранг соседства менее информативен, чем расстояние (ранги могут быть выведены из расстояний, но расстояния не могут быть выведены из рангов), и, таким образом, его сохранение легче.

Топологически ограниченное изометрическое вложение

Топологически ограниченное изометрическое вложение (TCIE)^[44] представляет собой алгоритм, основанный на приближении геодезических расстояний после фильтрации геодезических, несовместимых с евклидовой метрикой. Направленный на исправление искажений, вызванных использованием Isomap для отображения изначально невыпуклых данных, TCIE использует MDS взвешенных наименьших квадратов для получения более точного отображения. Алгоритм TCIE сначала обнаруживает возможные граничные точки в данных, и во время вычисления геодезической длины отмечает несовместимые геодезические, которым нужно присвоить небольшой вес во взвешенном Мажоризация стресса что следует.

Приближение и проекция равномерного многообразия

Аппроксимация и проекция однородного многообразия (UMAP) - это метод нелинейного уменьшения размерности.^[45] Визуально он похож на t-SNE, но предполагает, что данные равномерно распределены на локально связанный Риманово многообразие и что Риманова метрика является локально постоянным или приблизительно локально постоянным.^[46]

Методы на основе матриц близости

Метод, основанный на матрицах близости, - это метод, в котором данные представляются алгоритму в виде матрица сходства или матрица расстояний. Все эти методы подпадают под более широкий класс метрическое многомерное масштабирование. Вариации, как правило, заключаются в различиях в способах вычисления данных близости; Например, Isomap, локально линейные вложения, раскрытие максимальной дисперсии, и Картирование Саммона (которое на самом деле не является отображением) являются примерами методов многомерного метрического масштабирования.

Смотрите также

• Дискриминантный анализ
• Эластичная карта
• Особенности обучения
• Растущая самоорганизующаяся карта (ВШМ)
• Самоорганизующаяся карта (SOM)
• Теорема взятого
• Теорема вложения Уитни

Рекомендации

1. Лоуренс, Нил Д. (2012). «Объединяющая вероятностная перспектива для уменьшения спектральной размерности: идеи и новые модели». Журнал исследований в области машинного обучения. 13 (Май): 1609–1638. arXiv:1010.4830. Bibcode:2010arXiv1010.4830L.
2. Джон А. Ли, Мишель Верлейсен, Нелинейное уменьшение размерности, Springer, 2007.
3. Гашлер М. и Мартинес Т. Уменьшение временной нелинейной размерности, В Труды Международной совместной конференции по нейронным сетям IJCNN'11, стр.1959–1966, 2011
4. Иллюстрация подготовлена ​​с использованием бесплатного программного обеспечения: E.M. Mirkes, Анализ основных компонентов и самоорганизующиеся карты: апплет. Университет Лестера, 2011 г.
5. Инь, Худжунь; Изучение нелинейных главных многообразий с помощью самоорганизующихся карт, в А. Горбан, Б. Кегль, Д.К. Вунш, А.Зиновьев (ред.), Основные многообразия для визуализации данных и уменьшения размерности, Конспект лекций по информатике и инженерии (LNCSE), т. 58, Берлин, Германия: Springer, 2007, гл. 3. С. 68-95. ISBN  978-3-540-73749-0
6. Б. Шёлкопф, А. Смола, К.-Р. Мюллер, Нелинейный компонентный анализ как проблема собственных значений ядра. Нейронные вычисления 10(5):1299-1319, 1998, MIT Press Кембридж, Массачусетс, США, DOI: 10.1162 / 089976698300017467
7. Джихун Хэм, Дэниел Д. Ли, Себастьян Мика, Бернхард Шёлкопф. Ядровый взгляд на уменьшение размерности многообразий. Материалы 21-й Международной конференции по машинному обучению, Банф, Канада, 2004 г. DOI: 10.1145 / 1015330.1015417
8. Горбань, А. Н .; Зиновьев, А. (2010). «Принципиальные многообразия и графы на практике: от молекулярной биологии до динамических систем». Международный журнал нейронных систем. 20 (3): 219–232. arXiv:1001.1122. Дои:10.1142 / S0129065710002383. PMID  20556849. S2CID  2170982.
9. А. Зиновьев, ВиДаЭксперт - Средство визуализации многомерных данных (бесплатно для некоммерческого использования). Institut Curie, Париж.
10. А. Зиновьев, Обзор ViDaExpert, IHES (Institut des Hautes Études Scientifiques ), Бюрес-сюр-Иветт, Иль-де-Франс.
11. Хасти, Т. (ноябрь 1984 г.). Основные кривые и поверхности (PDF) (Кандидатская диссертация). Стэнфордский центр линейных ускорителей, Стэнфордский университет.
12. Горбань, А.; Kégl, B .; Wunsch, D.C .; Зиновьев А., ред. (2007). Основные многообразия для визуализации данных и уменьшения размерности. Конспект лекций по информатике и инженерии (LNCSE). Vol. 58. Берлин - Гейдельберг - Нью-Йорк: Спрингер. ISBN  978-3-540-73749-0.
13. Белкин, Михаил; Нийоги, Партха (2001). "Собственные карты Лапласа и спектральные методы для вложения и кластеризации". Достижения в системах обработки нейронной информации. MIT Press. 14: 586–691.
14. Белкин, Михаил (август 2003). Проблемы обучения на многообразиях (Кандидатская диссертация). Департамент математики Чикагского университета. Код Matlab для лапласовских собственных карт можно найти в алгоритмах на Ohio-state.edu
15. Бенхио, Йошуа; и другие. (2004). "Расширения вне выборки для LLE, Isomap, MDS, собственных карт и спектральной кластеризации" (PDF). Достижения в системах обработки нейронной информации.
16. Tenenbaum, J .; Фриман, В. (2000). «Разделение стиля и содержания с помощью билинейных моделей». Нейронные вычисления. 12 (6): 1247–1283. Дои:10.1162/089976600300015349. PMID  10935711. S2CID  9492646.
17. Левандовски, М .; Martinez-del Rincon, J .; Макрис, Д .; Небель, Ж.-К. (2010). «Временное расширение лапласовских собственных карт для неконтролируемого уменьшения размерности временных рядов». Труды Международной конференции по распознаванию образов (ICPR).
18. Левандовски, М .; Макрис, Д .; Веластин, С. А .; Небель, Ж.-К. (2014). "Структурные собственные карты лапласа для моделирования множеств многомерных последовательностей". IEEE Transactions по кибернетике. 44 (6): 936–949. Дои:10.1109 / TCYB.2013.2277664. PMID  24144690. S2CID  110014.
19. Martinez-del-Rincon, J .; Левандовски, М .; Nebel, J.-C .; Макрис, Д. (2014). «Обобщенные собственные лапласовские карты для моделирования и отслеживания движений человека». IEEE Transactions по кибернетике. 44 (9): 1646–1660. Дои:10.1109 / TCYB.2013.2291497. PMID  25137692. S2CID  22681962.
20. Дж. Б. Тененбаум, В. де Сильва, Дж. К. Лэнгфорд, Глобальная геометрическая основа для уменьшения нелинейной размерности, Science 290, (2000), 2319–2323.
21. С. Т. Роуис и Л. К. Саул, Уменьшение нелинейной размерности локально линейным вложением, Science Vol 290, 22 декабря 2000 г., 2323–2326.
22. Donoho, D .; Граймс, К. (2003). «Собственные карты Гессе: методы локально линейного вложения для данных большой размерности». Proc Natl Acad Sci U S A. 100 (10): 5591–5596. Дои:10.1073 / pnas.1031596100. ЧВК  156245. PMID  16576753.
23. З. Чжан и Дж. Ван, «MLLE: модифицированное локально линейное вложение с использованием множественных весов» http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.70.382
24. Сидху, Гаган (2019). «Локально линейное внедрение и выбор признаков фМРТ в психиатрической классификации». Журнал IEEE по трансляционной инженерии в здравоохранении и медицине. 7: 1–11. arXiv:1908.06319. Дои:10.1109 / JTEHM.2019.2936348. ЧВК  6726465. PMID  31497410. S2CID  201832756.
25. Чжан, Чжэньюэ; Хунюань Чжа (2005). "Основные многообразия и уменьшение нелинейной размерности посредством локального выравнивания касательного пространства". Журнал SIAM по научным вычислениям. 26 (1): 313–338. CiteSeerX  10.1.1.211.9957. Дои:10,1137 / с1064827502419154.
26. Бенхио, Йошуа; Монперрус, Мартин; Ларошель, Хьюго (октябрь 2006 г.). «Нелокальная оценка структуры многообразия» (PDF). Нейронные вычисления. 18 (10): 2509–2528. Дои:10.1162 / neco.2006.18.10.2509. ISSN  0899-7667. PMID  16907635. S2CID  1416595.
27. Н. Лоуренс, Вероятностный нелинейный анализ главных компонент с моделями латентных переменных гауссовского процесса, Journal of Machine Learning Research 6 (ноябрь): 1783–1816, 2005.
28. М. Дин, Г. Фань, Многослойные совместные многообразия поз походки для моделирования движения человека, IEEE Transactions on Cybernetics, Volume: 45, Issue: 11, Nov 2015.
29. van der Maaten, L.J.P .; Хинтон, Г. (Ноябрь 2008 г.). «Визуализация многомерных данных с помощью t-SNE» (PDF). Журнал исследований в области машинного обучения. 9: 2579–2605.
30. Джеймс X. Ли, Визуализация многомерных данных с помощью реляционной карты перспективы, Визуализация информации (2004) 3, 49–59
31. Taylor, D .; Климм, Ф .; Harrington, H.A .; Kramár, M .; Mischaikow, K .; Портер, М. А .; Муха, П. Дж. (2015). «Анализ топологических данных карт заражения для изучения процессов распространения в сетях». Nature Communications. 6: 7723. Дои:10.1038 / ncomms8723. ЧВК  4566922. PMID  26194875.
32. Demartines, P .; Эро, Ж. (1997). «Анализ криволинейных компонентов: самоорганизующаяся нейронная сеть для нелинейного отображения наборов данных» (PDF). IEEE-транзакции в нейронных сетях. 8 (1): 148–154. Дои:10.1109/72.554199. PMID  18255618.
33. Сунь, Джиган; Кроу, Малькольм; Файф, Колин (2010). «Анализ криволинейных компонент и расходимости Брегмана» (PDF). Европейский симпозиум по искусственным нейронным сетям (Esann). d-сторонние публикации. С. 81–86.
34. Кристиан Вальдер и Бернхард Шёлкопф, Диффеоморфное уменьшение размерности., Достижения в системах обработки нейронной информации 22, 2009 г., стр. 1713–1720, MIT Press
35. Ван, Чанг; Махадеван, Шридхар (июль 2008 г.). Выравнивание коллектора с использованием анализа Прокруста (PDF). 25-я Международная конференция по машинному обучению. С. 1120–1127.
36. Лафон, Стефан (май 2004 г.). Карты диффузии и геометрические гармоники (Кандидатская диссертация). Йельский университет.
37. Coifman, Ronald R .; Лафон, Стефан (19 июня 2006 г.). «Карты диффузии». Наука.
38. Ба, Б. (2008). Карты диффузии: приложения и анализ (Дипломная работа). Оксфордский университет.
39. Venna, J .; Каски, С. (2006). «Локальное многомерное масштабирование». Нейронные сети. 19 (6–7): 889–899. Дои:10.1016 / j.neunet.2006.05.014. PMID  16787737.
40. Scholz, M .; Каплан, Ф .; Guy, C.L .; Kopka, J .; Селбиг, Дж. (2005). «Нелинейный PCA: подход с отсутствием данных». Биоинформатика. Издательство Оксфордского университета. 21 (20): 3887–3895. Дои:10.1093 / биоинформатика / bti634. PMID  16109748.
41. С. Леспинац, М. Верлейсен, А. Хирон, Б. Фертил, DD-HDS: инструмент для визуализации и исследования многомерных данных, IEEE Transactions on Neural Networks 18 (5) (2007) 1265–1279.
42. Гашлер, М., Вентура, Д. и Мартинес, Т., Итеративное уменьшение нелинейной размерности с помощью моделирования многообразия, In Platt, J.C., Koller, D. и Singer, Y., и Roweis, S., редактор, Advances in Neural Information Processing Systems 20, pp. 513–520, MIT Press, Cambridge, MA, 2008
43. Леспинац С., Фертил Б., Вильмен П. и Эро Дж., Rankvisu: Отображение из сети квартала, Нейрокомпьютеры, т. 72 (13–15), стр. 2964–2978, 2009.
44. Росман Г., Бронштейн М. М., Бронштейн А. М. и Киммель Р., Уменьшение нелинейной размерности за счет изометрического вложения с топологическими ограничениями, Международный журнал компьютерного зрения, том 89, номер 1, 56–68, 2010 г.
45. Макиннес, Лиланд; Хили, Джон; Мелвилл, Джеймс (2018-12-07). «Приближение и проекция равномерного многообразия для уменьшения размерности». arXiv:1802.03426.
46. "UMAP: аппроксимация и проекция однородного коллектора для уменьшения размеров - документация umap 0.3". umap-learn.readthedocs.io. Получено 2019-05-04.

внешняя ссылка

• Isomap
• Генеративное топографическое картирование
• Тезис Майка Типпинга
• Модель латентных переменных гауссовского процесса
• Локально линейное вложение
• Карта реляционной перспективы
• Вафли - это библиотека C ++ с открытым исходным кодом, содержащая реализации LLE, Manifold Sculpting и некоторых других алгоритмов обучения многообразию.
• Домашняя страница DD-HDS
• Домашняя страница RankVisu
• Краткий обзор Diffusion Maps
• Нелинейный PCA нейронными сетями автоэнкодера