Круг Морса - Mohrs circle
Эта статья нужны дополнительные цитаты для проверка. (Декабрь 2014 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
Круг Мора двумерное графическое представление закон трансформации для Тензор напряжений Коши.
Круг Мора часто используется в расчетах, касающихся машиностроение за прочность материалов, геотехническая инженерия за прочность почв, и Строительная инженерия на прочность построенных конструкций. Он также используется для расчета подчеркивает во многих плоскостях, уменьшив их до вертикальных и горизонтальных компонентов. Они называются главными плоскостями, в которых основные напряжения рассчитываются; Круг Мора также можно использовать для нахождения главных плоскостей и главных напряжений в графическом представлении, и это один из самых простых способов сделать это.[1]
После выполнения анализ напряжения на материальном теле, принимаемом за континуум, компоненты тензора напряжений Коши в конкретной материальной точке известны относительно система координат. Затем круг Мора используется для графического определения составляющих напряжения, действующих на повернутую систему координат, т.е. действующих на иначе ориентированную плоскость, проходящую через эту точку.
В абсцисса и ордината (,) каждой точки на окружности - это значения нормального напряжения и напряжение сдвига компоненты, соответственно, действующие на повернутую систему координат. Другими словами, круг - это локус точек, которые представляют состояние напряжения на отдельных плоскостях при всех их ориентациях, где оси представляют главные оси элемента напряжения.
Немецкий инженер 19 века Карл Калманн был первым, кто задумал графическое представление напряжений с учетом продольных и вертикальных напряжений в горизонтальных балках во время изгиб. Его работа вдохновила коллег-немецкого инженера. Кристиан Отто Мор (тезка круга), который распространил его как на двумерные, так и на трехмерные напряжения и разработал отказ критерий, основанный на напряжении круга.[2]
Альтернативные графические методы для представления напряженного состояния в точке включают Эллипсоид напряжений Ламе и Квадрика напряжений Коши.
Круг Мора можно применить к любому симметричный 2x2 тензор матрица, включая напряжение и момент инерции тензоры.
Мотивация

Между частицами деформируемого объекта возникают внутренние силы, принимаемые за континуум, как реакция на приложенные внешние силы, т. е. либо поверхностные силы или же силы тела. Эта реакция следует из Законы движения Эйлера для континуума, которые эквивалентны Законы движения Ньютона для частицы. Мера интенсивности этих внутренних силы называется стресс. Поскольку объект считается континуумом, эти внутренние силы непрерывно распределяются в объеме объекта.
В инженерии, например, структурный, механический, или же геотехнический, распределение напряжений внутри объекта, например напряжения в горной породе вокруг туннеля, крыльев самолета или колонн зданий, определяется с помощью анализ напряжения. Расчет распределения напряжений подразумевает определение напряжений в каждой точке (материальной частице) объекта. В соответствии с Коши, то стресс в любой момент в объекте (рис. 2), рассматриваемом как континуум, полностью определяется девятью составляющими напряжения второго порядка тензор из тип (2,0) известный как Тензор напряжений Коши, :

После определения распределения напряжений в объекте относительно системы координат , может потребоваться вычислить компоненты тензора напряжений в конкретной материальной точке относительно повернутой системы координат , т.е. напряжения, действующие на плоскость с другой ориентацией, проходящую через эту интересующую точку, образующие угол с системой координат (Рисунок 3). Например, интересно найти максимальное нормальное напряжение и максимальное напряжение сдвига, а также ориентацию плоскостей, на которые они действуют. Для этого необходимо выполнить тензорное преобразование при повороте системы координат. Из определения тензор тензор напряжений Коши подчиняется тензорный закон преобразования. Графическим представлением этого закона преобразования для тензора напряжений Коши является круг Мора для напряжения.
Круг Мора для двумерного напряженного состояния

В двух измерениях тензор напряжений в данной материальной точке относительно любых двух перпендикулярных направлений полностью определяется всего тремя составляющими напряжения. Для конкретной системы координат эти компоненты напряжения: нормальные напряжения и , и напряжение сдвига . Из баланса углового момента можно продемонстрировать симметрию тензора напряжений Коши. Эта симметрия означает, что . Таким образом, тензор напряжений Коши можно записать как:
Цель состоит в том, чтобы использовать круг Мора, чтобы найти компоненты напряжения. и в повернутой системе координат , т.е. на другой ориентированной плоскости, проходящей через и перпендикулярно - самолет (рисунок 4). Повернутая система координат делает угол с исходной системой координат .
Уравнение круга Мора
Чтобы вывести уравнение круга Мора для двумерных случаев плоское напряжение и плоская деформация, сначала рассмотрим двухмерный бесконечно малый материальный элемент вокруг материальной точки (Рисунок 4) с единичной площадью в направлении, параллельном - плоскость, т. е. перпендикулярная странице или экрану.
Из равновесия сил на бесконечно малом элементе величины нормального напряжения и напряжение сдвига даны:
Вывод параметрических уравнений круга Мора - Равновесие сил Из равновесия сил в направлении (-оси) (рис. 4), зная, что площадь плоскости, на которой действует , у нас есть: Однако, зная, что
мы получаем
Теперь из равновесия сил в направлении (-оси) (Рисунок 4), зная, что площадь плоскости, на которой действует , у нас есть:
Однако, зная, что
мы получаем
Оба уравнения также могут быть получены путем применения закона преобразования тензора к известному тензору напряжений Коши, что эквивалентно выполнению статического равновесия сил в направлении и .
Вывод параметрических уравнений круга Мора - тензорное преобразование Закон преобразования тензора напряжений можно сформулировать как Расширяя правую часть, и зная, что и , у нас есть:
Однако, зная, что
мы получаем
Однако, зная, что
мы получаем
В данный момент нет необходимости рассчитывать составляющую напряжения. действующий на плоскости, перпендикулярной плоскости действия поскольку это не требуется для вывода уравнения для круга Мора.
Эти два уравнения являются параметрические уравнения круга Мора. В этих уравнениях - параметр, а и - координаты. Это означает, что, выбрав систему координат с абсциссой и ордината , присваивая значения параметру расположит полученные точки по окружности.
Устранение параметра из этих параметрических уравнений получим непараметрическое уравнение круга Мора. Этого можно добиться, переписав уравнения для и , сначала транспонируя первый член в первом уравнении и возводя в квадрат обе части каждого из уравнений, а затем складывая их. Таким образом, мы имеем
куда
Это уравнение круг (круг Мора) формы
с радиусом с центром в точке с координатами в система координат.
Знаковые соглашения
Есть два отдельных набора условных обозначений, которые необходимо учитывать при использовании круга Мора: одно условное обозначение для компонентов напряжения в «физическом пространстве», а другое - для компонентов напряжения в «пространстве круга Мора». Кроме того, в каждом из двух наборов соглашений о знаках Инженерная механика (Строительная инженерия и машиностроение ) литература следует другому соглашению о знаках, чем геомеханика литература. Не существует стандартного соглашения о знаках, и на выбор конкретного соглашения о знаках влияет удобство расчета и интерпретации для конкретной задачи. Более подробное объяснение этих условных обозначений представлено ниже.
Предыдущий вывод уравнения Круга Мора с использованием рисунка 4 соответствует условию знаков инженерной механики. В этой статье мы будем использовать условные обозначения инженерной механики..
Соглашение о знаках физического пространства
Согласно соглашению о тензоре напряжений Коши (рис. 3 и рис. 4), первый индекс в компонентах напряжения обозначает поверхность, на которую действует компонент напряжения, а второй индекс указывает направление компонента напряжения. Таким образом - напряжение сдвига, действующее на грань с вектором нормали в положительном направлении -оси, и в положительном направлении -ось.
В знаковом соглашении физического пространства положительные нормальные напряжения направлены наружу к плоскости действия (растяжение), а отрицательные нормальные напряжения направлены внутрь плоскости действия (сжатие) (рис. 5).
В соответствии с соглашением о знаках физического пространства положительные касательные напряжения действуют на положительные грани материального элемента в положительном направлении оси. Кроме того, положительные касательные напряжения действуют на отрицательные грани материального элемента в отрицательном направлении оси. Положительная грань имеет нормальный вектор в положительном направлении оси, а отрицательная грань имеет нормальный вектор в отрицательном направлении оси. Например, касательные напряжения и положительны, потому что они действуют на положительные стороны, и они также действуют в положительном направлении ось и -оси соответственно (рисунок 3). Аналогично, соответствующие противоположные касательные напряжения и действующие в отрицательных гранях имеют отрицательный знак, потому что они действуют в отрицательном направлении ось и -оси соответственно.
Конвенция о знаках пространства и круга Мора
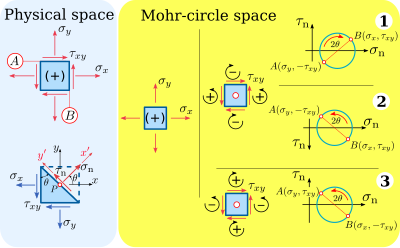
В соглашении о знаках круга Мора и пространства нормальные напряжения имеют тот же знак, что и нормальные напряжения в соглашении о знаках физического пространства: положительные нормальные напряжения действуют наружу к плоскости действия, а отрицательные нормальные напряжения действуют внутрь, к плоскости действия.
Напряжения сдвига, однако, имеют другое соглашение в пространстве круга Мора по сравнению с соглашением в физическом пространстве. Согласно соглашению о знаке пространства-круга Мора, положительные касательные напряжения вращают материальный элемент против часовой стрелки, а отрицательные касательные напряжения вращают материал по часовой стрелке. Таким образом, составляющая напряжения сдвига положительна в пространстве круга Мора, а составляющая напряжения сдвига отрицательна в пространстве круга Мора.
Существуют два варианта рисования пространства кругов Мора, которые дают математически правильный круг Мора:
- Положительные касательные напряжения нанесены вверх (рисунок 5, условное обозначение № 1).
- Положительные касательные напряжения отложены вниз, т.е. - ось перевернута (рис. 5, соглашение о знаках №2).
Нанесение положительных касательных напряжений вверх дает угол на круге Мора имеют положительное вращение по часовой стрелке, что противоположно правилам физического пространства. Вот почему некоторые авторы[3] предпочитают наносить положительные напряжения сдвига вниз, что делает угол на круге Мора имеют положительное вращение против часовой стрелки, аналогично соглашению о физическом пространстве для касательных напряжений.
Чтобы преодолеть "проблему" того, что ось касательного напряжения направлена вниз в пространстве круга Мора, существует альтернатива соглашение о знаках, в котором предполагается, что положительные касательные напряжения поворачивают материальный элемент по часовой стрелке, а отрицательные касательные напряжения предполагают вращение материального элемента против часовой стрелки (рисунок 5, вариант 3). Таким образом, положительные касательные напряжения отображаются вверх в пространстве круга Мора, а угол имеет положительное вращение против часовой стрелки в пространстве круга Мора. Этот альтернатива условное обозначение создает круг, который идентичен условному обозначению № 2 на рисунке 5, потому что положительное напряжение сдвига также является напряжением сдвига против часовой стрелки, и оба графика нанесены вниз. Кроме того, отрицательное напряжение сдвига - напряжение сдвига по часовой стрелке, и оба графика показаны вверх.
Эта статья следует соглашению о знаках инженерной механики для физического пространства и альтернатива соглашение о знаках для пространства круга Мора (соглашение о знаках № 3 на рисунке 5)
Рисование круга Мора

Предполагая, что мы знаем компоненты напряжения , , и в какой-то момент в исследуемом объекте, как показано на рисунке 4, ниже приведены шаги для построения круга Мора для состояния напряжений при :
- Нарисуйте декартову систему координат с горизонтальным ось и вертикаль -ось.
- Постройте две точки и в пространство, соответствующее известным компонентам напряжения в обеих перпендикулярных плоскостях и соответственно (рис. 4 и 6), следуя выбранному соглашению о знаках.
- Нарисуйте диаметр круга путем соединения точек и с прямой линией .
- Нарисуйте круг Мора. Центр круга - это середина диаметральной линии , что соответствует пересечению этой прямой с ось.
Нахождение основных нормальных напряжений
Величина основные напряжения абсциссы точек и (Рисунок 6), где круг пересекает -ось. Величина главного главного напряжения всегда является наибольшим абсолютным значением абсцисс любой из этих двух точек. Аналогично, величина незначительного главного напряжения всегда наименьшее абсолютное значение абсцисс этих двух точек. Как и ожидалось, ординаты этих двух точек равны нулю, что соответствует величине составляющих напряжения сдвига на главных плоскостях. В качестве альтернативы значения главных напряжений можно найти по формуле
где величина средний нормальный стресс абсцисса центра , данный
и длина радиус окружности (на основе уравнения окружности, проходящей через две точки), определяется как
Определение максимального и минимального касательного напряжения
Максимальные и минимальные касательные напряжения соответствуют ординатам наивысшей и самой низкой точек на окружности соответственно. Эти точки расположены на пересечении круга с вертикальной линией, проходящей через центр круга, . Таким образом, величина максимального и минимального касательных напряжений равна значению радиуса окружности
Нахождение компонент напряжений на произвольной плоскости
Как упоминалось ранее, после выполнения двумерного анализа напряжений мы знаем компоненты напряжения , , и в материальной точке . Эти компоненты напряжения действуют в двух перпендикулярных плоскостях. и проходя через как показано на рисунках 5 и 6. Круг Мора используется для нахождения компонентов напряжения и , т.е. координаты любой точки на окружности, действующей на любой другой плоскости проходя через делать угол с самолетом . Для этого можно использовать два подхода: двойной угол и полюс или начало координат.
Двойной угол
Как показано на рисунке 6, для определения составляющих напряжения действующий на самолете под углом против часовой стрелки к плоскости на котором действует, мы путешествуем под углом в том же направлении против часовой стрелки по окружности от известной точки напряжения В точку , т.е. угол между строк и в круге Мора.
Подход двойного угла основан на том факте, что угол между векторами нормали к любым двум физическим плоскостям, проходящим через (Рисунок 4) - половина угла между двумя линиями, соединяющими их соответствующие точки напряжения. на круге Мора и центре круга.
Это соотношение двойного угла происходит из того факта, что параметрические уравнения для круга Мора являются функцией . Также видно, что самолеты и в материальном элементе вокруг на рисунке 5 разделены углом , который в круге Мора представлен угол (удвоить угол).
Полюс или происхождение самолетов

Второй подход включает определение точки на окружности Мора, называемой столб или происхождение самолетов. Любая прямая линия, проведенная от полюса, будет пересекать круг Мора в точке, которая представляет состояние напряжения на плоскости, наклоненной в той же ориентации (параллельно) в пространстве, что и эта линия. Следовательно, зная компоненты напряжения и на любой конкретной плоскости можно провести линию, параллельную этой плоскости, через определенные координаты и на круге Мора и найдите полюс как точку пересечения такой линии с кругом Мора. В качестве примера предположим, что у нас есть стрессовое состояние с компонентами напряжения. , , и , как показано на рисунке 7. Сначала мы можем провести линию из точки параллельно плоскости действия , или, если мы выберем иное, прямую из точки параллельно плоскости действия . Пересечение любой из этих двух прямых с кругом Мора является полюсом. Как только полюс определен, найти состояние напряжения на плоскости, образующей угол с вертикалью, или, другими словами, плоскость, вектор нормали которой образует угол с горизонтальной плоскостью, то мы можем провести линию от полюса, параллельную этой плоскости (см. рисунок 7). Нормальные напряжения и напряжения сдвига в этой плоскости являются координатами точки пересечения линии и круга Мора.
Определение ориентации главных плоскостей
Ориентация плоскостей, в которых действуют максимальные и минимальные главные напряжения, также известная как основные самолеты, можно определить, измерив в круге Мора углы BOC и ∠BOE, соответственно, и взяв половину каждого из этих углов. Таким образом, угол ∠BOC между и вдвое больше угла что главная главная плоскость делает с плоскостью .
Углы и также можно найти из следующего уравнения
Это уравнение определяет два значения для которые врозь (рисунок). Это уравнение может быть получено непосредственно из геометрии круга или путем составления параметрического уравнения круга для равны нулю (напряжение сдвига в главных плоскостях всегда равно нулю).
Пример


Предположим, что элемент материала находится в напряженном состоянии, как показано на рисунках 8 и 9, с плоскостью одной из его сторон, ориентированной на 10 ° по отношению к горизонтальной плоскости. С помощью круга Мора найдите:
- Ориентация их планов действий.
- Максимальные касательные напряжения и ориентация их плоскостей действия.
- Компоненты напряжений на горизонтальной плоскости.
Проверьте ответы, используя формулы преобразования напряжений или закон преобразования напряжений.
Решение:Следуя соглашению о знаках инженерной механики для физического пространства (рис. 5), компоненты напряжения для материального элемента в этом примере следующие:
- .
Следуя инструкциям по рисованию круга Мора для этого конкретного состояния напряжения, мы сначала рисуем декартову систему координат с - ось вверх.
Затем мы наносим две точки A (50,40) и B (-10, -40), представляющие состояние напряжения в плоскостях A и B, как показано на рисунках 8 и 9. Эти точки соответствуют соглашению о знаках инженерной механики для пространство круга Мора (рис. 5), которое предполагает положительные нормальные напряжения наружу от материального элемента и положительные касательные напряжения на каждой плоскости, вращающей материальный элемент по часовой стрелке. Таким образом, напряжение сдвига, действующее на плоскость B, отрицательно, а напряжение сдвига, действующее на плоскость A, положительно. Диаметр окружности - это линия, соединяющая точки A и B. Центр окружности является пересечением этой линии с линией -ось. Зная расположение центра и длину диаметра, мы можем построить круг Мора для этого конкретного состояния напряжения.
Абсциссы обеих точек E и C (Рисунок 8 и Рисунок 9), пересекающие -оси - величины минимального и максимального нормальных напряжений соответственно; ординаты обеих точек E и C представляют собой величины касательных напряжений, действующих как на малую, так и на большую главные плоскости, соответственно, которые равны нулю для главных плоскостей.
Несмотря на то, что идея использования круга Мора заключается в графическом нахождении различных компонентов напряжения путем фактического измерения координат различных точек на окружности, удобнее подтверждать результаты аналитически. Таким образом, радиус и абсцисса центра окружности равны
и основные напряжения
Координаты для обеих точек H и G (Рисунок 8 и Рисунок 9) - это величины минимального и максимального касательного напряжения, соответственно; абсциссы для обеих точек H и G представляют собой значения нормальных напряжений, действующих в тех же плоскостях, где действуют минимальное и максимальное касательные напряжения, соответственно. Величины минимального и максимального касательных напряжений могут быть найдены аналитически с помощью
и нормальные напряжения, действующие в тех же плоскостях, где действуют минимальное и максимальное касательные напряжения, равны
Для определения ориентации основных нормальных напряжений и главных касательных напряжений мы можем выбрать либо метод двойного угла (рис. 8), либо подход полюса (рис. 9).
Используя метод двойного угла, мы измеряем углы BOC и ∠BOE в круге Мора (рис. 8), чтобы найти удвоенный угол главного главного напряжения и второстепенного главного напряжения, которые создают с плоскостью B в физическом пространстве. Чтобы получить более точное значение этих углов, вместо ручного измерения углов можно использовать аналитическое выражение
Одно из решений: . Из рисунка 8 это значение соответствует углу BOE. Таким образом, малый главный угол равен
Тогда главный главный угол равен
Помните, что в этом конкретном примере и - углы относительно плоскости действия (ориентирована в -оси), а не углы по отношению к плоскости действия (ориентирована в -ось).
Используя подход Pole, мы сначала локализуем полюс или начало координат самолетов. Для этого проведем через точку A на окружности Мора линию, наклоненную на 10 ° к горизонтали, или, другими словами, линию, параллельную плоскости A, где действует. Полюс - это место, где эта линия пересекает круг Мора (рис. 9). Чтобы подтвердить местоположение полюса, мы могли бы провести линию через точку B на круге Мора, параллельную плоскости B, где действует. Эта линия также пересекает круг Мора на полюсе (рис. 9).
От полюса мы проводим линии к разным точкам круга Мора. Координаты точек, где эти линии пересекают круг Мора, указывают компоненты напряжения, действующие на плоскость в физическом пространстве, имеющую тот же наклон, что и линия. Например, линия от полюса до точки C в круге имеет тот же наклон, что и плоскость в физическом пространстве, где действует. Эта плоскость составляет 63,435 ° с плоскостью B как в пространстве круга Мора, так и в физическом пространстве. Таким же образом проводят линии от полюса до точек E, D, F, G и H, чтобы найти компоненты напряжения на плоскостях с одинаковой ориентацией.
Круг Мора для общего трехмерного состояния напряжений

Чтобы построить круг Мора для общего трехмерного случая напряжений в точке, значения основные напряжения и их основные направления необходимо сначала оценить.
Рассматривая главные оси как систему координат, а не общую , , системе координат и предполагая, что , то нормальные и сдвиговые компоненты вектора напряжений , для данной плоскости с единичным вектором , удовлетворяют следующим уравнениям
Знаю это , мы можем решить для , , , с использованием Метод исключения Гаусса что дает
С , и неотрицательно, числители этих уравнений удовлетворяют
- как знаменатель и
- как знаменатель и
- как знаменатель и
Эти выражения можно переписать как
которые представляют собой уравнения трех окружностей Мора для напряжений , , и , с радиусами , , и , а их центры с координатами , , , соответственно.
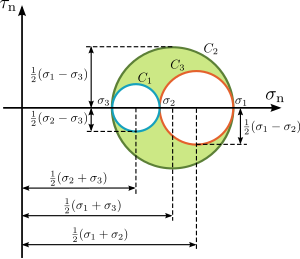
Эти уравнения для кругов Мора показывают, что все точки допустимых напряжений лежат на этих кругах или в пределах затененной области, заключенной ими (см. рисунок 10). Точки стресса удовлетворяющий уравнению для круга лежать на круге или за его пределами . Точки стресса удовлетворяющий уравнению для круга лежать на круге или внутри него . И наконец, стрессовые моменты удовлетворяющий уравнению для круга лежать на круге или за его пределами .
Смотрите также
Рекомендации
- ^ «Главное напряжение и главная плоскость». www.engineeringapps.net. Получено 2019-12-25.
- ^ Парри, Ричард Хоули Грей (2004). Круги Мора, пути напряжений и геотехника (2-е изд.). Тейлор и Фрэнсис. С. 1–30. ISBN 0-415-27297-1.
- ^ Гир, Джеймс М. (2013). Механика материалов. Гудно, Барри Дж. (8-е изд.). Стэмфорд, Коннектикут: Cengage Learning. ISBN 9781111577735.
Библиография
- Пиво, Фердинанд Пьер; Элвуд Рассел Джонстон; Джон Т. ДеВольф (1992). Механика материалов. McGraw-Hill Professional. ISBN 0-07-112939-1.
- Brady, B.H.G .; E.T. Браун (1993). Механика горных пород для подземных горных работ (Третье изд.). Kluwer Academic Publisher. С. 17–29. ISBN 0-412-47550-2.
- Davis, R.O .; Сельвадурай. А. П. С. (1996). Упругость и геомеханика. Издательство Кембриджского университета. С. 16–26. ISBN 0-521-49827-9.
- Хольц, Роберт Д .; Ковач, Уильям Д. (1981). Введение в геотехническую инженерию. Серия «Прентис-Холл» по гражданскому строительству и инженерной механике. Прентис-Холл. ISBN 0-13-484394-0.
- Джагер, Джон Конрад; Кук, штат Нью-Джерси; Циммерман, Р.В. (2007). Основы механики горных пород (Четвертое изд.). Вили-Блэквелл. С. 9–41. ISBN 978-0-632-05759-7.
- Юмикис, Альфредс Р. (1969). Теоретическая механика грунтов: с практическими приложениями к механике грунтов и фундаментостроению. Van Nostrand Reinhold Co. ISBN 0-442-04199-3.
- Парри, Ричард Хоули Грей (2004). Круги Мора, пути напряжений и геотехника (2-е изд.). Тейлор и Фрэнсис. С. 1–30. ISBN 0-415-27297-1.
- Тимошенко, Стивен П .; Джеймс Норман Гудье (1970). Теория упругости (Третье изд.). Международные издания McGraw-Hill. ISBN 0-07-085805-5.
- Тимошенко, Стивен П. (1983). История прочности материалов: с кратким изложением истории теории упругости и теории конструкций.. Дуврские книги по физике. Dover Publications. ISBN 0-486-61187-6.





![{ boldsymbol { sigma}} = left [{{ begin {matrix} sigma _ {{11}} & sigma _ {{12}} & sigma _ {{13}} sigma _ {{21}} & sigma _ {{22}} & sigma _ {{23}} sigma _ {{31}} & sigma _ {{32}} & sigma _ {{33} } end {matrix}}} right] Equiv left [{{ begin {matrix} sigma _ {{xx}} & sigma _ {{xy}} & sigma _ {{xz} } sigma _ {{yx}} & sigma _ {{yy}} & sigma _ {{yz}} sigma _ {{zx}} & sigma _ {{zy}} & sigma _ {{zz}} end {matrix}}} right] Equiv left [{{ begin {matrix} sigma _ {x} & tau _ {{xy}} & tau _ {{xz}} tau _ {{yx}} & sigma _ {y} & tau _ {{yz}} tau _ {{zx}} & tau _ {{zy}} & sigma _ {z} end {matrix}}} right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/150f0bb6d0473b0cc572e736e3f0c61ae490cf0e)







![{ boldsymbol { sigma}} = left [{{ begin {matrix} sigma _ {x} & tau _ {{xy}} & 0 tau _ {{xy}} & sigma _ { y} & 0 0 & 0 & 0 end {matrix}} right] Equiv left [{{ begin {matrix} sigma _ {x} & tau _ {{xy}} tau _ {{xy}} & sigma _ {y} end {matrix}}} right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/946034030fac5e3d547e35f94ac672ed9dbc87d2)













![{ begin {align} { boldsymbol { sigma}} '& = { mathbf A} { boldsymbol { sigma}} { mathbf A} ^ {T} left [{{ begin {matrix } sigma _ {{x '}} & tau _ {{x'y'}} tau _ {{y'x '}} & sigma _ {{y'}} end { matrix}}} right] & = left [{{ begin {matrix} a _ {{x}} & a _ {{xy}} a _ {{yx}} & a _ {{y}} end { матрица}}} right] left [{{ begin {matrix} sigma _ {{x}} & tau _ {{xy}} tau _ {{yx}} & sigma _ {{ y}} end {matrix}}} right] left [{{ begin {matrix} a _ {{x}} & a _ {{yx}} a _ {{xy}} & a _ {{y}] } end {matrix}} right] & = left [{{ begin {matrix} cos theta & sin theta - sin theta & cos theta end {matrix}}} right] left [{{ begin {matrix} sigma _ {{x}} & tau _ {{xy}} tau _ {{yx}} & sigma _ {{y}} end {matrix}}} right] left [{{ begin {matrix} cos theta & - sin theta sin theta & cos theta конец {матрица}}} право] конец {выровнено}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c98aac6cba73c966e89d772397263f69ee507e4d)







![{ begin {align} left [ sigma _ {{ mathrm {n}}} - { tfrac {1} {2}} ( sigma _ {x} + sigma _ {y}) right] ^ {2} + tau _ {{ mathrm {n}}} ^ {2} & = left [{ tfrac {1} {2}} ( sigma _ {x} - sigma _ {y} ) right] ^ {2} + tau _ {{xy}} ^ {2} ( sigma _ {{ mathrm {n}}} - sigma _ {{ mathrm {avg}}}) ^ {2} + tau _ {{ mathrm {n}}} ^ {2} & = R ^ {2} end {выровнено}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2774a663ddaa56d3418815d5a7d05fcf456d6f12)
![R = { sqrt { left [{ tfrac {1} {2}} ( sigma _ {x} - sigma _ {y}) right] ^ {2} + tau _ {{xy}} ^ {2}}} quad { text {and}} quad sigma _ {{ mathrm {avg}}} = { tfrac {1} {2}} ( sigma _ {x} + sigma _ {y})](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a7f5d5e3408c2d465f9e463c5576810f83d2401)























![R = { sqrt { left [{ tfrac {1} {2}} ( sigma _ {x} - sigma _ {y}) right] ^ {2} + tau _ {{xy}} ^ {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb62b3753948e2c8cbcc4b054de4f34d9630d711)



















![{ begin {align} R & = { sqrt { left [{ tfrac {1} {2}} ( sigma _ {x} - sigma _ {y}) right] ^ {2} + tau _ {{xy}} ^ {2}}} & = { sqrt { left [{ tfrac {1} {2}} (- 10-50) right] ^ {2} + 40 ^ { 2}}} & = 50 { textrm {МПа}} конец {выровнено}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f970da4c989f682a80bda6bb2ceb4285812314d)


































![{ begin {align} tau _ {{ mathrm {n}}} ^ {2} + left [ sigma _ {{ mathrm {n}}} - { tfrac {1} {2}} ( sigma _ {2} + sigma _ {3}) right] ^ {2} geq left ({ tfrac {1} {2}} ( sigma _ {2} - sigma _ {3} ) right) ^ {2} tau _ {{ mathrm {n}}} ^ {2} + left [ sigma _ {{ mathrm {n}}} - { tfrac {1} { 2}} ( sigma _ {1} + sigma _ {3}) right] ^ {2} leq left ({ tfrac {1} {2}} ( sigma _ {1} - sigma _ {3}) right) ^ {2} tau _ {{ mathrm {n}}} ^ {2} + left [ sigma _ {{ mathrm {n}}} - { tfrac {1} {2}} ( sigma _ {1} + sigma _ {2}) right] ^ {2} geq left ({ tfrac {1} {2}} ( sigma _ {1 } - sigma _ {2}) right) ^ {2} конец {выровнено}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d28046575eb3837044e07c9c8b3c6d70e641087b)






![left [{ tfrac {1} {2}} ( sigma _ {2} + sigma _ {3}), 0 right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/d32d3b2fb09d202625baa0df42fc08db094ce4c5)
![left [{ tfrac {1} {2}} ( sigma _ {1} + sigma _ {3}), 0 right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/be6108f95fb1e9bf64d2e770f8e220e91505d59b)
![left [{ tfrac {1} {2}} ( sigma _ {1} + sigma _ {2}), 0 right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/04758ef4c7e5169326291b5857f30c6ae9f83dee)