Самолет Лагерра - Laguerre plane

В математика, а Самолет Лагерра один из Самолеты Benz: the Самолет Мебиуса, Самолет Лагерра и Самолет Минковского, названный в честь Французский математик Эдмон Николя Лагер.

классический самолет Лагерра: 2d / 3d-модель

По сути, классическая плоскость Лагерра - это структура заболеваемости который описывает поведение кривых ${\displaystyle y=ax^{2}+bx+c}$ , т.е. параболы и линии, в настоящий аффинная плоскость. Чтобы упростить конструкцию, на любую кривую ${\displaystyle y=ax^{2}+bx+c}$ смысл ${\displaystyle (\infty ,a)}$ добавлен. Еще одно преимущество этого завершения: геометрия плоскости завершенных парабол / линий изоморфный к геометрии плоские сечения из цилиндр (Смотри ниже).

Классический реальный самолет Лагерра

Первоначально классическая плоскость Лагерра была определена как геометрия ориентированных прямых и окружностей на реальной евклидовой плоскости (см. ^[1]). Здесь мы предпочитаем параболическую модель классической плоскости Лагерра.

Мы определяем:

${\displaystyle {\mathcal {P}}:=\mathbb {R} ^{2}\cup (\{\infty \}\times \mathbb {R} ),\ \infty \notin \mathbb {R} ,}$ набор точки,${\displaystyle {\mathcal {Z}}:=\{\{(x,y)\in \mathbb {R} ^{2}\mid y=ax^{2}+bx+c\}\cup \{(\infty ,a)\}\mid a,b,c\in \mathbb {R} \}}$ набор циклы.

Структура заболеваемости ${\displaystyle ({\mathcal {P}},{\mathcal {Z}},\in )}$ называется классический самолет Лагерра.

Набор точек ${\displaystyle \mathbb {R} ^{2}}$ плюс копия ${\displaystyle \mathbb {R} }$ (см. рисунок). Любая парабола / линия ${\displaystyle y=ax^{2}+bx+c}$ получает дополнительный балл ${\displaystyle (\infty ,a)}$.

Точки с одинаковой координатой x не могут быть соединены кривыми ${\displaystyle y=ax^{2}+bx+c}$. Следовательно, мы определяем:

Две точки ${\displaystyle A,B}$ находятся параллельно (${\displaystyle A\parallel B}$)если ${\displaystyle A=B}$ или нет цикла, содержащего ${\displaystyle A}$ и ${\displaystyle B}$.

Для описания классической вещественной плоскости Лагерра над двумя точками ${\displaystyle (a_{1},a_{2}),(b_{1},b_{2})}$ параллельны тогда и только тогда, когда ${\displaystyle a_{1}=b_{1}}$. ${\displaystyle \parallel }$ является отношение эквивалентности, похожий на параллельность линий.

Структура заболеваемости ${\displaystyle ({\mathcal {P}},{\mathcal {Z}},\in )}$ обладает следующими свойствами:

Лемма:

• По любым трем точкам ${\displaystyle A,B,C}$, попарно не параллельны, существует ровно один цикл ${\displaystyle z}$ содержащий ${\displaystyle A,B,C}$.
• Для любой точки ${\displaystyle P}$ и любой цикл ${\displaystyle z}$ есть ровно одна точка ${\displaystyle P'\in z}$ такой, что ${\displaystyle P\parallel P'}$.
• Для любого цикла ${\displaystyle z}$, любая точка ${\displaystyle P\in z}$ и любой момент ${\displaystyle Q\notin z}$ это не параллельно ${\displaystyle P}$ есть ровно один цикл ${\displaystyle z'}$ через ${\displaystyle P,Q}$ с ${\displaystyle z\cap z'=\{P\}}$, т.е. ${\displaystyle z}$ и ${\displaystyle z'}$ трогать друг друга в ${\displaystyle P}$.

Laguerre-plane: стереографическая проекция плоскости x-z на цилиндр

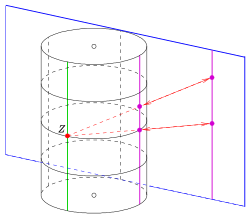
Подобно сферической модели классической Самолет Мебиуса Существует модель цилиндра для классической плоскости Лагерра:

${\displaystyle ({\mathcal {P}},{\mathcal {Z}},\in )}$ изоморфна геометрии плоских сечений кругового цилиндра в ${\displaystyle \mathbb {R} ^{3}}$ .

Следующее отображение ${\displaystyle \Phi }$ это проекция с центром ${\displaystyle (0,1,0)}$ который отображает плоскость x-z на цилиндр с помощью уравнения ${\displaystyle u^{2}+v^{2}-v=0}$, ось ${\displaystyle (0,{\tfrac {1}{2}},..)}$ и радиус ${\displaystyle r={\tfrac {1}{2}}\ :}$

${\displaystyle \Phi :\ (x,z)\rightarrow ({\frac {x}{1+x^{2}}},{\frac {x^{2}}{1+x^{2}}},{\frac {z}{1+x^{2}}})=(u,v,w)\ .}$

• Точки ${\displaystyle (0,1,a)}$ (линия на цилиндре через центр) появляются не как изображения.
• ${\displaystyle \Phi }$ проектирует парабола / линия с уравнением ${\displaystyle z=ax^{2}+bx+c}$ в самолет ${\displaystyle w-a=bu+(a-c)(v-1)}$. Итак, изображение параболы / линии представляет собой плоское сечение цилиндра с неперпендикулярной плоскостью и, следовательно, окружность / эллипс без точки ${\displaystyle (0,1,a)}$. Параболы / линия ${\displaystyle z=ax^{2}+a}$ отображаются на (горизонтальные) окружности.
• Линия (a = 0) отображается на окружность / эллипс через центр ${\displaystyle (0,1,0)}$ и парабола ( ${\displaystyle a\neq 0}$) на круг / эллипс, не содержащие ${\displaystyle (0,1,0)}$.

Аксиомы плоскости Лагерра

Из приведенной выше леммы вытекает следующее определение:

Позволять ${\displaystyle {\mathcal {L}}:=({\mathcal {P}},{\mathcal {Z}},\in )}$ быть структурой инцидентов с точка набор ${\displaystyle {\mathcal {P}}}$ и набор циклы ${\displaystyle {\mathcal {Z}}}$.
Две точки ${\displaystyle A,B}$ находятся параллельно (${\displaystyle A\parallel B}$) если ${\displaystyle A=B}$ или нет цикла, содержащего ${\displaystyle A}$ и ${\displaystyle B}$.
${\displaystyle {\mathcal {L}}}$ называется Самолет Лагерра если верны следующие аксиомы:

Плоскость Лагерра: аксиомы

B1: По любым трем точкам ${\displaystyle A,B,C}$, попарно не параллельны, существует ровно один цикл ${\displaystyle z}$ который содержит ${\displaystyle A,B,C}$.

БИ 2: Для любой точки ${\displaystyle P}$ и любой цикл ${\displaystyle z}$ есть ровно одна точка ${\displaystyle P'\in z}$ такой, что ${\displaystyle P\parallel P'}$.

B3: Для любого цикла ${\displaystyle z}$, любая точка ${\displaystyle P\in z}$ и любой момент ${\displaystyle Q\notin z}$ это не параллельно ${\displaystyle P}$ есть ровно один цикл ${\displaystyle z'}$ через ${\displaystyle P,Q}$ с ${\displaystyle z\cap z'=\{P\}}$,

т.е. ${\displaystyle z}$ и ${\displaystyle z'}$ трогать друг друга в ${\displaystyle P}$.

B4: Любой цикл содержит не менее трех точек, есть хотя бы один цикл. По крайней мере четыре точки не входят в цикл.

Четыре балла ${\displaystyle A,B,C,D}$ находятся конциклический если есть цикл ${\displaystyle z}$ с ${\displaystyle A,B,C,D\in z}$.

Из определения отношения ${\displaystyle \parallel }$ и аксиома Би 2 мы получили

Лемма:Связь ${\displaystyle \parallel }$ является отношение эквивалентности.

Следуя цилиндрической модели классической плоскости Лагерра, введем обозначение:

а) Для ${\displaystyle P\in {\mathcal {P}}}$ мы установили ${\displaystyle {\overline {P}}:=\{Q\in {\mathcal {P}}\ |\ P\parallel Q\}}$.b) Класс эквивалентности ${\displaystyle {\overline {P}}}$ называется генератор.

Для классической плоскости Лагерра образующая - это линия, параллельная оси y (плоская модель) или линия на цилиндре (космическая модель).

Связь с линейной геометрией дается следующим определением:

Для самолета Лагерра ${\displaystyle {\mathcal {L}}:=({\mathcal {P}},{\mathcal {Z}},\in )}$ мы определяем локальную структуру

${\displaystyle {\mathcal {A}}_{P}:=({\mathcal {P}}\setminus \{{\overline {P}}\},\{z\setminus \{{\overline {P}}\}\ |\ P\in z\in {\mathcal {Z}}\}\cup \{{\overline {Q}}\ |\ Q\in {\mathcal {P}}\setminus \{{\overline {P}}\},\in )}$

и назовите это остаток в точке P.

В плоской модели классической плоскости Лагерра ${\displaystyle {\mathcal {A}}_{\infty }}$ это настоящая аффинная плоскость ${\displaystyle \mathbb {R} ^{2}}$.В общем получаем

Теорема: Любой вычет в плоскости Лагерра является аффинная плоскость.

И эквивалентное определение самолета Лагерра:

Теорема:Структура инцидентности вместе с отношением эквивалентности ${\displaystyle \parallel }$ на ${\displaystyle {\mathcal {P}}}$ является плоскостью Лагерра тогда и только тогда, когда для любой точки ${\displaystyle P}$ остаток ${\displaystyle {\mathcal {A}}_{P}}$ аффинная плоскость.

Конечные плоскости Лагерра

минимальная модель плоскости Лагерра (показаны только 4 из 8 циклов)

Следующая структура заболеваемости представляет собой минимальная модель самолета Лагерра:

${\displaystyle {\mathcal {P}}:=\{A_{1},A_{2},B_{1},B_{2},C_{1},C_{2}\}\ ,}$

${\displaystyle {\mathcal {Z}}:=\{\{A_{i},B_{j},C_{k}\}\ |\ i,j,k=1,2\}\ ,}$

${\displaystyle A_{1}\parallel A_{2},\ B_{1}\parallel B_{2},\ C_{1}\parallel C_{2}\ .}$

Следовательно ${\displaystyle |{\mathcal {P}}|=6}$ и ${\displaystyle |{\mathcal {Z}}|=8\ .}$

Для конечных плоскостей Лагерра, т. Е. ${\displaystyle |{\mathcal {P}}|<\infty }$, мы получили:

Лемма:Для любых циклов ${\displaystyle z_{1},z_{2}}$ и любой генератор ${\displaystyle {\overline {P}}}$ из конечный Самолет Лагерра${\displaystyle {\mathcal {L}}:=({\mathcal {P}},{\mathcal {Z}},\in )}$ у нас есть:

${\displaystyle |z_{1}|=|z_{2}|=|{\overline {P}}|+1}$.

Для конечной плоскости Лагерра ${\displaystyle {\mathcal {L}}:=({\mathcal {P}},{\mathcal {Z}},\in )}$ и цикл ${\displaystyle z\in {\mathcal {Z}}}$ целое число ${\displaystyle n:=|z|-1}$ называется порядок из ${\displaystyle {\mathcal {L}}}$.

Из комбинаторики получаем

Лемма:Позволять ${\displaystyle {\mathcal {L}}:=({\mathcal {P}},{\mathcal {Z}},\in )}$ быть Лагерром - плоскостью порядок ${\displaystyle n}$. потом

а) любой остаток ${\displaystyle {\mathcal {A}}_{P}}$ аффинная плоскость порядка ${\displaystyle n\quad ,}$ б) ${\displaystyle |{\mathcal {P}}|=n^{2}+n,}$ в) ${\displaystyle |{\mathcal {Z}}|=n^{3}.}$

Самолеты Микели Лагерра

В отличие от плоскостей Мебиуса формальное обобщение классической модели плоскости Лагерра, т. Е. Замена ${\displaystyle \mathbb {R} }$ произвольным полем ${\displaystyle K}$, ведет в любом слючае на примере самолета Лагерра.

Теорема:Для поле ${\displaystyle K}$ и

${\displaystyle {\mathcal {P}}:=K^{2}\cup }$ ${\displaystyle (\{\infty \}\times K),\ \infty \notin K}$,

${\displaystyle {\mathcal {Z}}:=\{\{(x,y)\in K^{2}\ |\ y=ax^{2}+bx+c\}\cup \{(\infty ,a)\}\ |\ a,b,c\in K\}}$ структура заболеваемости

${\displaystyle {\mathcal {L}}(K):=({\mathcal {P}},{\mathcal {Z}},\in )}$ является плоскостью Лагерра со следующим соотношением параллельности: ${\displaystyle (a_{1},a_{2})\parallel (b_{1},b_{2})}$ если и только если ${\displaystyle a_{1}=b_{1}}$.

Аналогично плоскости Мёбиуса верна лагерровская версия теоремы Микеля:

Теорема Микеля (круги вместо парабол)

Теорема MIQUEL:Для самолета Лагерра ${\displaystyle {\mathcal {L}}(K)}$ верно следующее:

Если для любых 8 попарно не параллельных точек ${\displaystyle P_{1},\ldots ,P_{8}}$ который может быть назначен вершинам куба так, что точки на 5 гранях соответствуют конциклическим четверкам, тогда шестая четверка точек также будет конциклической.

(Для лучшего обзора на рисунке вместо парабол нарисованы круги)

Важность теоремы Микеля показывает следующая теорема, связанная с v. D. Варден, Смид и Чен:

Теорема: Только самолет Лагерра ${\displaystyle {\mathcal {L}}(K)}$ удовлетворяет теореме Микеля.

В силу последней теоремы ${\displaystyle {\mathcal {L}}(K)}$ называется микелианский самолет Лагерра.

Замечание: В минимальная модель плоскости Лагерра является микелевой.

Он изоморфен плоскости Лагерра. ${\displaystyle {\mathcal {L}}(K)}$ с ${\displaystyle K=GF(2)}$ (поле ${\displaystyle \{0,1\}}$).

Замечание: Подходящий стереографическая проекция показывает: ${\displaystyle {\mathcal {L}}(K)}$ изоморфна геометрии плоских сечений квадратичного цилиндра над полем ${\displaystyle K}$.

Овоидальные самолеты Лагерра

Есть много самолетов Лагерра, которые не микелианский (см. ссылку ниже). Класс, наиболее похожий на микелевы плоскости Лагерра, - это овоидальные плоскости Лагерра. Овоидальная плоскость Лагерра - это геометрия плоских секций цилиндра, построенная с помощью овал вместо невырожденной коники. Овал - это квадратичное множество и обладает теми же геометрическими свойствами, что и невырожденная коника на проективной плоскости: 1) прямая пересекает овал в нуле, одной или двух точках и 2) в любой точке существует единственная касательная. Простой овал в реальной плоскости можно построить, склеив вместе две подходящие половинки разных эллипсов, так что в результате получится не коническая форма. Даже в конечном случае существуют овалы (см. квадратичное множество ).

Смотрите также

• Преобразования Лагерра

Рекомендации

1. Бенц, Уолтер (2013) [1973], Vorlesungen über Geometrie der Algebren (на немецком языке), Гейдельберг: Springer, п. 11, ISBN  9783642886713

внешняя ссылка

• Самолет Benz в SpringerLink
• Лекция Плоские окружности геометрии, Введение в плоскости Мебиуса, Лагерра и Минковского, стр. 67